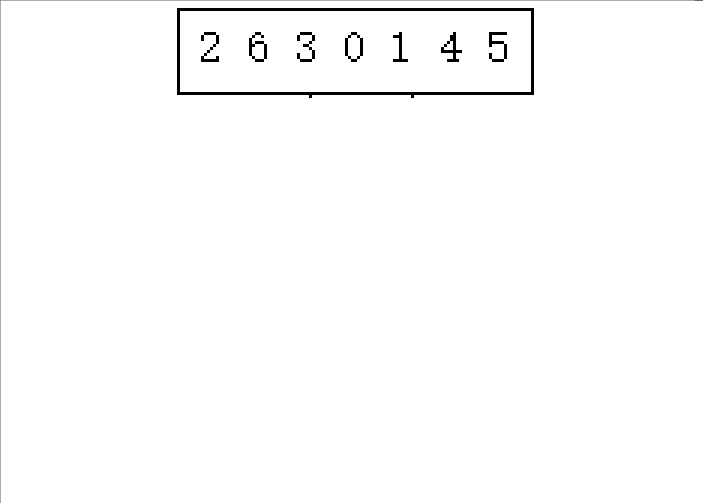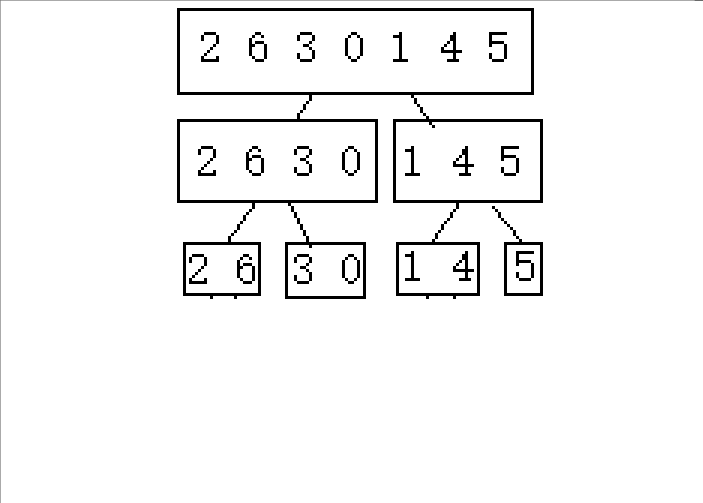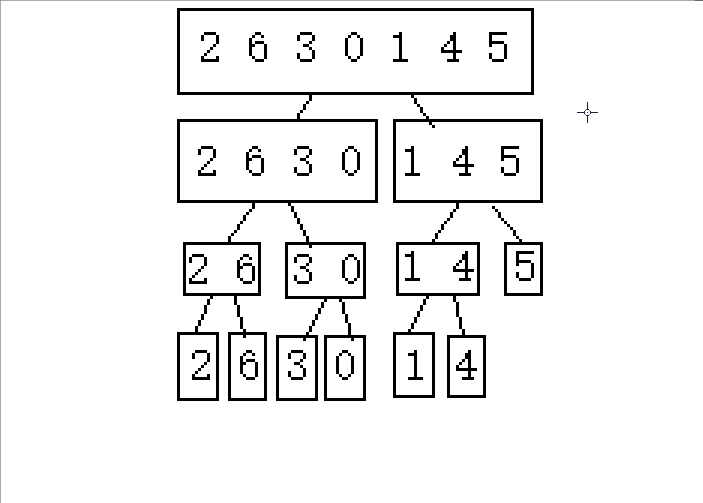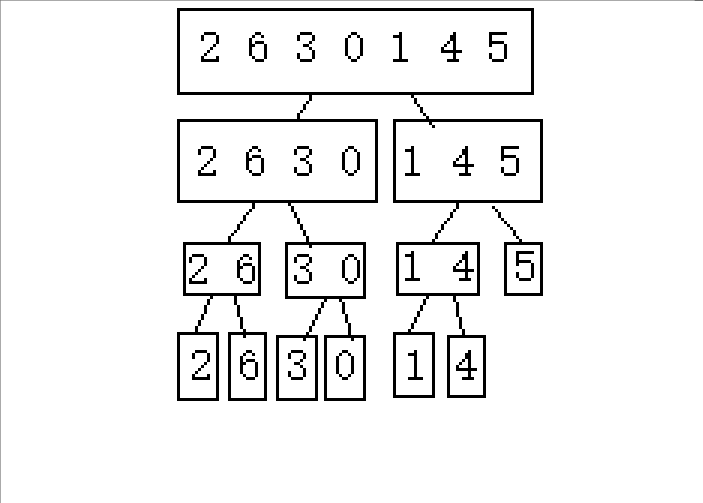【c语言】归并排序
目录
前言:
归并排序
1.递归版本
演示:
实现:
2.非递归版本
演示:
实现:
前言:
❥(ゝω・✿ฺ) hi~ 欢迎大家点开我的文章~ 这里我会介绍归并排序的两种实现方法:递归和非递归。
注:下面算法我均是使用的升序,降序只需要在执行条件相反就好了~<*))>>=<
归并排序
归并排序是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并:归并实际上就是先将这个整体分成两部分,然后这两部分要是有序,就进行归并操作,结合成一个整体就有序了,如果这两个子部分没有序的就继续分,分到单体或者不存在的时候就有序了,然后再逐步回溯。
分治:“分而治之”,意思就是把一个复杂的问题分成几个小问题,然后再分,分到可以简单求解,然后原问题的解实际上就是这些小问题的解的合并。这里的应用就是将其分成小块进行排序,最后集中到一起在排一次就排序好了。
1.递归版本
演示:
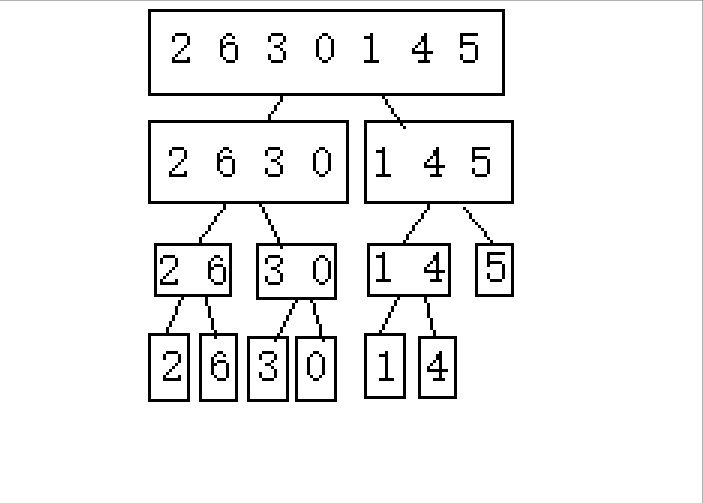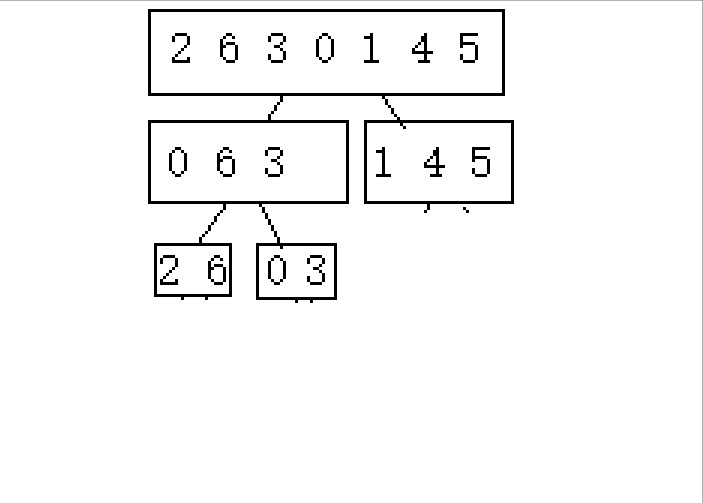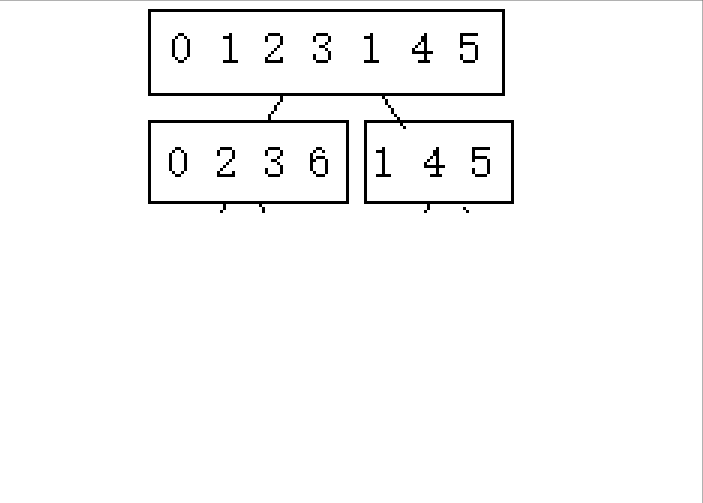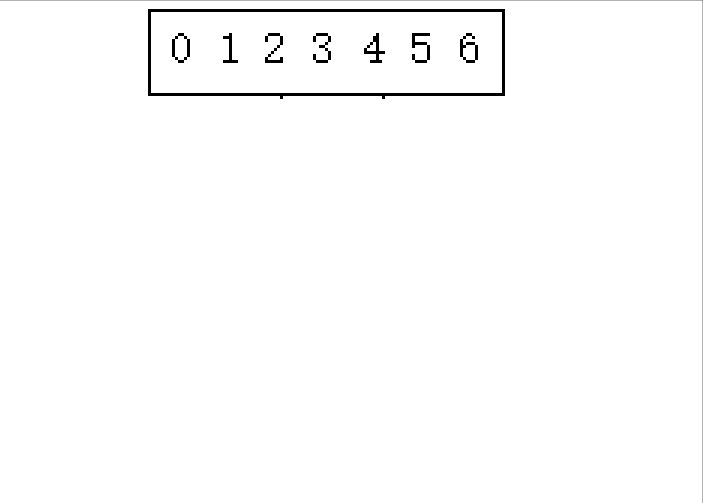
(下面以2 6 3 0 1 4 5这串待排序数组进行演示)
1.逐步分成可解决问题(单个或者不存在即就是有序的)
2.从后往前归并
实现:
经过上面的演示,我们不难发现,首先是要将整个待排序数逐步分成小块,然后进行归并。这明显就有点类似后序算法,即你先把左右两边处理好,然后我在进行我的归并。
基于这一点,程序不难实现:
//辅助归并排序递归的子函数
void _MergeSort(int* a, int* tmp, int begin, int end)
{
if (begin >= end)
return;//单个或者不存在其区间就结束递归
//类似于后序:
int middle = (begin + end) / 2;
int begin1 = begin;
int end1 = middle;
int begin2 = middle + 1;
int end2 = end;
_MergeSort(a, tmp, begin1, end1);
_MergeSort(a, tmp, begin2, end2);
//此时认为 [begin1, end1] 和 [begin2, end2]两段区间上有序
//归并算法
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));//内存操作函数,可以将整个数组的数复制过去
}
//归并排序 递归版本
void MergeSort(int* a, int n)
{
//首先malloc一个数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("未能申请到内存\n");
exit(-1);
}
//第一次传入 0 和 n - 1 传入闭区间
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
}
tmp数组:我们在归并时,需要一个媒介来进行数字的交换。如果就在原数组上进行操作的话,会覆盖掉原来的数据,造成数据丢失。
malloc: void *malloc( size_t size ); 向堆内存申请指定字节的连续空间。
memcpy:void* memcpy(void* dest, const void* src, size_t count);将一段指定字节的连续空间的内容复制到dest。
_MergeSort:用于递归的子函数,在实现归并的前面,首先将两边递归进去,直到发现满足begin >= end的时候就结束递归,回溯上一个递归的函数进行下一步操作,这样就能保证在进行归并前,两个区间均有序。
2.非递归版本
递归版本由于数据量过大的话,迭代过多,会导致栈溢出,如果我们能实现非递归版本,使其借用堆内存进行排序,堆内存比栈内存大多了,就不用担心溢出的问题了。
非递归版本实现有点特殊。相信大家也了解过快速排序的非递归版本,那个是利用的栈或者队列数据结构来存储区间从而实现的。但是是否适用于这里的归并排序呢。
通过前面的递归版本我们知道,此归并排序是要在前面排好后也就是后序的形式对这两个区间的数进行归并。如果利用栈来存这些区间,首先存储0 到n - 1,然后存储 0 到middle,middle + 1到 end ,然后就不能直接取出,因为不能确定这两个区间是否是有序的,所以需要继续存进去区间,相对麻烦。
那么我们换个思路,不是所以的非递归实现需要借助类似于栈之类的数据空间的啊,比如斐波那契数列的非递归实现,那么我们直接实现是不是也可以呢?
演示:
1.属于2的n次方的排列数([0 7])
注意,在此演示中,每次均是被均分下来的,两份两份。为了实现代码的准确性,那么就要区分 不是2的n次方的奇数次和偶数次。
2.不属于2的n次方的奇数次排列([0 6])
这里就会发现,第一次对区间1进行2份2份的分下来的话3没有与其分的,那么3就保持不变,直到有2分分到它这一组的时候就可以正常进行了。
3.不属于2的n次方的偶数次排列([0 9])
这里同样的可以发现,第一次是均可以2分的,但是后面就不行了,所以在后面二分好了后,对应的没有组的也保持不变,直到对应有组。
实现:
直接进行分开,然后进行归并。此代码并不好写,主要是区分上面演示中的三种情况。
我们可以定义一个gap变量来确定每一次的区间长度,第一次1,第二次2,第三次4,直到 下面的程序中有两种处理方法,均针对于上述演示中的另外两种情况。 gap:gap被定义成每次划分的区间长度,下一次就是上一次两个区间合并一起的区域,所以gap每次循环*2即可。 begin:begin1和2分别是两个区间开始的下标。根据i的区分,i第一次是0,那么根据gap的区域长度,begin1自然是i,begin2就是已经跨过了一个区域了,所以是i+gap end:end1和2是两个区域结束的下标,end1是第一个区域的最后下标,自然是第二个区域的开始减一,所以是i+gap - 1.end2是第二个区域的最后下标,所以自然是第三个区域的开始减一,即i+gap*2-1。 对于两种特殊情况,有两种处理办法,实际上也就是一种,只不过针对于memcpy是一段一段复制还是整体复制做了区分。一个是不进行处理跳下一步,一个是要进行处理,对边界进行优化即可。//归并排序 非递归版本
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("申请空间失败\n");
exit(-1);
}
//整体交换 - 1
//int gap = 1;
//while (gap < n)
//{
// for (int i = 0; i < n; i += 2 * gap)//每次跨越两组
// {
// int begin1 = i, end1 = i + gap - 1; // [0, 0] [2, 2] [4, 4] [6, 6]
// int begin2 = i + gap, end2 = i + 2 * gap - 1; // [1, 1] [3, 3] [5, 5] [7, 7]
// //边界调整:begin1肯定不会越界,当end1越界的时候
// if (end1 >= n)
// {
// end1 = n - 1;
// //让2系列的不存在即可
// begin2 = 1;
// end2 = 0;
// }
// else if (begin2 >= n)
// {
// begin2 = 1;
// end2 = 0;
// }
// else if (end2 >= n)
// {
// end2 = n - 1;
// }
// //归并
// int j = begin1;
// while (begin1 <= end1 && begin2 <= end2)
// {
// if (a[begin1] <= a[begin2])
// {
// tmp[j++] = a[begin1++];
// }
// else
// {
// tmp[j++] = a[begin2++];
// }
// }
// while (begin1 <= end1)
// {
// tmp[j++] = a[begin1++];
// }
// while (begin2 <= end2)
// {
// tmp[j++] = a[begin2++];
// }
// }
// memcpy(a, tmp, sizeof(int) * n);//整体复制,那么 不是2的次方倍的n就要进行边界调整
// gap *= 2;
//}
//每次交换 - 2
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)//每次跨越两组
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (end1 >= n || begin2 >= n)
{
break;
}
else if (end2 >= n)
{
end2 = n - 1;
}
//归并
int j = begin1;
int m = end2 - begin1 + 1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * m);//局部复制,end2 - begin1 + 1
}
gap *= 2;
}
free(tmp);
}