快速排序和归并排序

引言：

大家好，我是小星星，今天要整理的知识点是——快速排序和归并排序。

一、快速排序

为什么要学习快速排序？
了解原理并能书写出来模板，对于我们刷题思路的提升有很大帮助。

思想：分治。分而治之 ，每次以边界点划分区间，多次选取边界点划分区间，直到分区间只有一个元素。直接返回数组。
时间复杂度：
最好的情况~O(nlogn)。
最坏的情况~O(n^2)。
分析详见下一篇文章。
快速排序的步骤：

1、确立分界点。先从已给数列中任意取出一个数作为分界点（此时是无序的），你可以选取左右端点或其它点，这里我们选取 x = q[(l + r) >>1]，因为它更快些。
2、调整区间。（重点理解）把所有小于等于 x 的数移到左边，把大于等于的数移到右边。双指针实现。
3、递归给左右两端排序。

重点说一下第二部分：利用双指针 i 和 j 调整区间。大致步骤是这样的：
1、i指针自 l 出发，当q[i]<=x时向右移动,q[i]>x时i指针停止移动。
2、移动 j 指针。j指针自r出发，当q[i]>=x时从右向左移动，q[i] 3、交换i指针，j指针。
可能的疑惑点：为什么 i=l-1，j=r+1？
——这是因为我们使用的是do，while语句，先移动指针，再判断指针与x的大小关系。

 int i = l - 1, j = r + 1, x = q[l + r >> 1];
    //首次执行while语句之前,i++,j--
    //这里 -1和 +1保证了i指针从L开始,j指针从r开始.
    while (i < j)//指针没有相遇
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);//交换指针
    }

然后分别递归处理左半边，右半边

quick_sort(q, l, j), quick_sort(q, j + 1, r);

一个快速排序就写好了，下面是模板代码。

void quick_sort(int q[], int l, int r)//传递数组地址
{
    if (l >= r) return;//递归出口

    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    // x = q[l+(l-r)>>1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j), quick_sort(q, j + 1, r);
    //递归处理左右两端
}

两道简单的练习题。
acwing785.快速排序
acwing786.第k个数

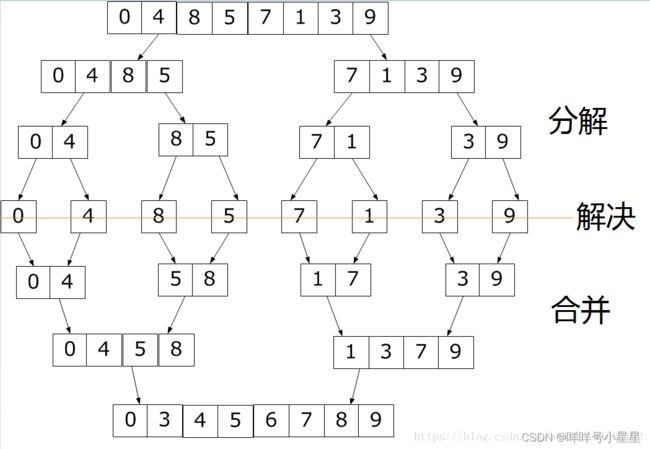
二、归并排序

思想：分治。分而治之 ，递归的把数据一分为二，直到数组中只有一个元素为止。归并的把两个有序数组重新排序。返回一个新数组。
时间复杂度：
比较稳定~O(nlogn)。
分析详见下一篇文章。
快速排序的步骤：

1、确定分界点。mid = (l + r) / 2.
2、递归排序左右两端，将一个数组从中间一分为二，形成左右两个数组。对左右两个数组继续按照刚才的方式递归的一分为二，直到数组只有一个元素为止。
3、归并，合二为一。（重难点）把两个有序数组合并为一个有序数组。合并时进行排序

下面是具体的实现

递归左右两边

int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);

归并一：如果左边小，那么先把左边放进新数组。否则把右边的放进新数组。

    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

归并二：一边循环完毕，另一边没有完毕。

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

最后把数组复原一下~

for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];

最终的模板代码如下~

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;
    //
    merge_sort(q, l, mid);
    merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];

    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];

    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

两道练习题，检验对模板的掌握。
acwing787.归并排序
acwing788.逆序对的数量

三、对比总结

相同点：
两个排序的基本思想都是分治——分而治之。
具体实现都用递归。

不同点：
1、快速排序：边分解边排序。每次分解都实现整体上有序，即参照值左侧的数都小于参照值，右侧的大于参照值；是自上而下的排序；
归并排序：先分解再合并。先递归分解到最小区间，然后从小去区间开始合并排序，是自下而上的归并排序；
2、选取分界点时，快速排序选的是值，一半比这个值大，一半比这个值小。
归并排序选的是数组地址，即下标。不用交换处理，直接把数组一切两半。
3、快速排序是原地排序，原地排序指的是空间复杂度为O(1)；
归并排序不是原地排序，因为两个有序数组的合并需要额外的空间协助才能合并；
4、快速排序是不稳定的，时间复杂度在O(nlogn)~O(n^2)之间 。归并排序是稳定的，时间复杂度是O(nlogn)。(复杂度的分析在下一篇文章）

四、写在最后

学习算法的重点是学习编程思维，这件事值得我们慢慢去做，做很久很久。漫漫长路，感谢有你~

如果各位大佬发现哪里有问题的话，欢迎指出~

如果你觉得我这篇文章对你有帮助的话，欢迎你订阅我的算法专栏并给我三连关注支持一下~，你们的支持是我更新的动力，感谢各位！