2-3树的插入和删除操作

注意：以下均用2-3树指代2-3查找树

2-3树的定义：

• 2-3树首先是一颗二叉查找树（BST树），也是一颗平衡二叉树（AVL树），所以同时包含两者的性质，
• 2-3树是一颗完美平衡的二叉树，也就是说所有叶子结点到根结点的路径都相同
• 2-3树中包含两种结点：2结点与3结点；如果是2结点，那么一定有一个值和两个孩子，如果是3结点，一定有两个值和3个孩子
• 它是一颗最简单的B树

2-3树结点定义：

template
class tree_23_node　　　　　　　　　　　　　　　　　　　　//2-3树的结点
{
    public:
        tree_23_node()；

    public:
        int m_type;        　　　　　　　　　　　　　　 //用于记录结点的类型，如果是2结点，那么m_type=2,如果是3结点，m_type=3,否则m_type=0;
        T* m_small_data;
        T* m_large_data;
　　　 　class tree_23_node*m_parent;             //父结点
        class tree_23_node*m_l_child;            //左孩子
        class tree_23_node*m_m_child;         　 //中孩子
        class tree_23_node*m_r_child;            //右孩子
}

template
class tree_23　　　　　　　　　　　　　　　　　　　　　　 //2-3树
{
　　public:
　　　　tree_23();

　　public:
　　　　class tree_23_node*m_root;
}

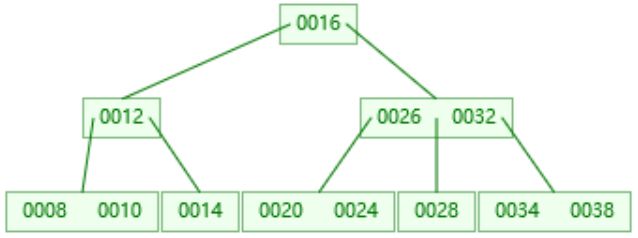
上图是一颗简单的2-3树，2-3树中序遍历的顺序为：左孩子->当前结点小值->（中结点->当前结点大值）->右孩子，

其中序遍历结果是：8  10  12  14  16  20  24  26  28  32  34  38

查找：

　　2-3树的查找操作和二叉树的查找操作是一样的，

• 检查当前结点的值，如果当前结点命中，返回true，退出递归；否则向左子树递归查找
• 如果左子树命中，返回true，退出递归；（如果中子树存在）否则向中子树递归查找
• 如果中子树命中，返回true，退出递归；否则向右子树递归查找
• 如果右子树命中，返回true，退出递归；否则当前结点、左子树、（如果存在）中子树、右子树都没有命中，返回false

插入：

　　注意：2-3树的长高发生在根结点，而不是叶子结点

　　普通二叉树的插入操作：假设插入的值为data，

• 先找到要插入的叶子结点位置，此叶子结点设为leaf，值为leaf-value
• 新建结点son ,son-value=data,son-l-child=son-r-child=NULL（son的左右孩子都是NULL）
• 再判断leaf-value和data的大小，如果data>leaf-value，则son到leaf的右子树中，否则son到leaf的左子树中
• 注意在上一步时树的高度变化了（树高+1），也就是说树的高度变化发生在叶子结点leaf

2-3树的插入分析：假设插入的值为data，

• 先找到要插入的叶子结点位置，此叶子结点设置为leaf，
• 如果此时新建结点son,son-value=data，插入到leaf的一颗子树中，2-3树的性质（所有叶子结点到根结点的路径都相同）不会满足
• 所以不能新建结点，而是要把data插入到叶子结点leaf中，这样（所有叶子结点到根结点的路径都相同）这条性质可能不会满足
• 如果leaf是2结点，新值data直接插入到leaf，如果leaf是3结点，不能插入新值data，那么将leaf分裂并向上（leaf的父结点）递归处理
• 如果递归到根结点，而根结点也是3结点，那么分裂根结点后，树的高度+1，也就是说2-3树的长高发生在根结点，而不是叶子结点

2-3树的插入操作：假设插入的值为data，

1. 如果根结点是NULL，直接将data插入根结点
2. 否则先找到data需要插入的叶子结点leaf
3. 如果如果插入结点leaf是2结点，直接插入data，leaf变为3结点
4. 如果插入结点leaf是3结点，向上（parent）递归寻求解（假设leaf的父结点为parent）
   1. 如果parent是2结点，这是情况2，直接插入parent并return
   2. 如果parent是3结点，这是情况3，继续向向上（parent->parnet）递归求解
   3. 如果parent是结点，单独处理

• 插入操作----情况1：根结点root==NULL，直接将data插入到根结点，根结点变为2结点
• 插入操作----情况2：根结点root！=NULL，首先找到插入的叶子结点leaf，　　

 情况2.1：leaf是2结点，直接向leaf插入data 　　

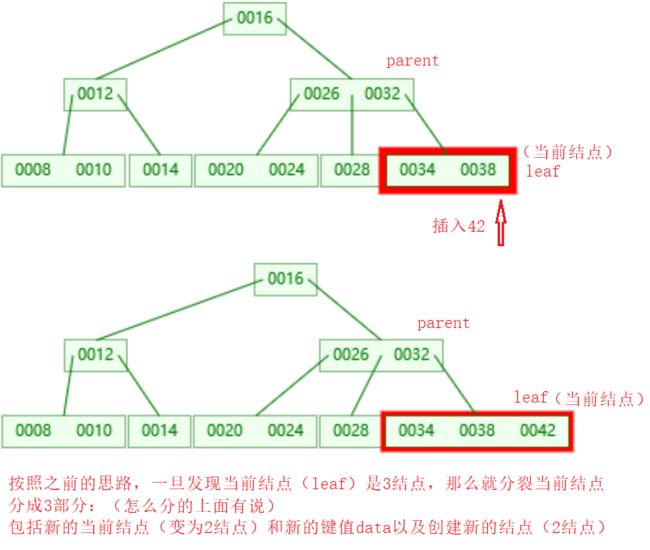
情况2.2：leaf是3结点，但是leaf的parent是2结点，（注意这里的leaf的孩子是NULL空指针，没有画出来）

情况2.2分析：

由于leaf是3结点，如果直接将9插入到leaf中，那么leaf会变成4结点（leaf会有3个值，4个孩子），不符合2-3树的性质；

解决办法：

• 将leaf中的两个值（small和large两个值）和data比较大小
• 最小的值作为leaf->m_small_data,并且leaf变为2结点，leaf->m_large_data=NULL
• 中间值作为新的data，最大值新建一个结点new_node
• 将data和new_node作为形参往parent递归下去（对parent递归）
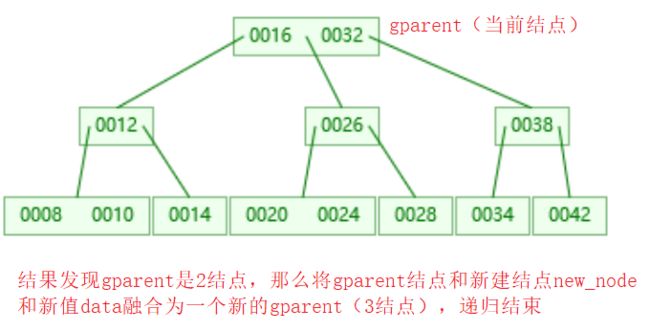
• 如果parent是2结点（包含一个键值和两个孩子），将data（键值）和new_node（孩子）与parent的一个键值和两个孩子组合为一个3结点（2个键值和3个孩子）
• 如果parent是3结点，就是下面的情况2.3　　　　

如下面的3张图，在创建  新的键值data和新的孩子new_node   时，要考虑数值之间的大小关系，详情见下面的图，并且data和new_node在和parent组成3结点时也要考虑清楚各种情况，总之很繁琐

情况2.3：leaf是3结点，但是leaf的parent也是3结点，（注意这里的leaf的孩子是NULL空指针，没有画出来）

情况2.4：leaf是3结点，但是leaf的parent也是3结点，并且parent是根结点

2-3树中插入的注意事项

1、当前结点分裂形成新的当前结点、新建结点、新值时，一定不能丢失所有的孩子信息，其中当前结点有3个孩子，以及上传的一个孩子（是什么呢？它是前一个新建结点，可以是NULL），共4个孩子，可以形成两个2结点

2、如果是根结点的分裂，要将根结点的m_root的指向及时更新

3、2-3树的长高只能通过根结点的分裂

删除：

　　注意：2-3树的逆生长（即高度降低）一定使发生在根结点，而不是叶子结点

　　普通二叉树的删除操作：假设删除的值为data

• 首先是找到待删除结点的位置
• 如果待删除结点是叶子结点，直接删除
• 如果待删除结点是非叶子结点，分情况讨论：
  1. 待删除结点只有一个孩子，那么直接将父结点和孩子结点建立联系即可
  2. 待删除结点有两个孩子，找到当前结点的前驱（后继）结点，两结点替换，继续对前驱结点进行结点删除操作

　　2-3树的删除操作：假设删除的值为data

1. 首先找到待删除结点的位置
2. 如果待删除结点不是叶子结点，将问题转化为删除叶子结点（通过与前驱或者后继结点替换来转换问题）
3. 如果待删除结点是叶子结点，
   1. 如果删除结点是3结点，直接删除data，删除结点变为2结点，然后return
   2. 如果删除结点是2结点，首先删除data，删除结点变为0结点
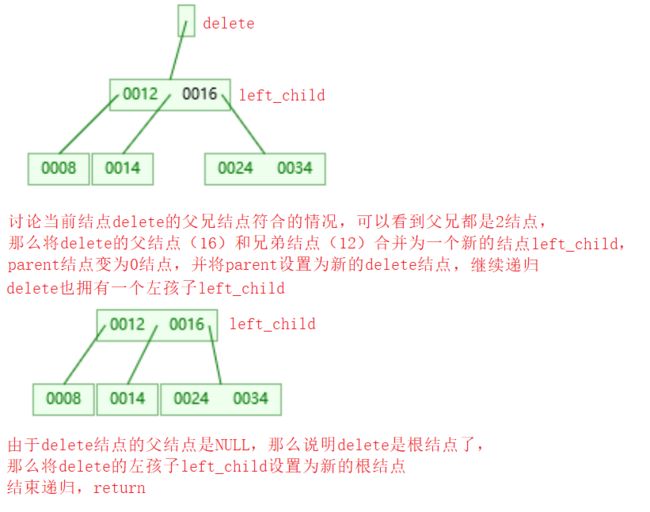
      1. 如果父兄都是2结点，递归处理
      2. 如果父兄至少有一个是3结点，从父结点或者兄弟结点借值后组建新的删除结点（变为2结点），然后return

　　下面我将通过图示来说明：待删除2-3树如下

删除操作----情况1：如果待删除结点不是叶子结点，将问题转化为删除叶子结点

删除操作----情况2：如果待删除结点是叶子结点

情况2.1：删除结点是3结点，直接删除data，删除结点变为2结点，然后return

情况2.2：删除结点是2结点，直接删除data，删除结点变为0结点

情况2.2.1：如果父兄至少有一个3结点，从父结点或者兄弟结点借值后组建新的删除结点（变为2结点），然后return

这种情况是最繁琐的，要分父兄都是2结点、父是2结点兄是3结点、父是3结点兄是2结点这3种情况考虑，还要考虑delete是在父结点的左结点、结点还是右结点，但是具体的操作是一样的，太繁琐了就不具体讨论了，本人共考虑了16小情况，还没有找到简单的解法

情况2.2.2：如果父兄都是2结点，此时待删除结点是0结点，需要递归处理

如果说情况2.2.1是繁琐，那么情况2.2.2就很简洁了，这里我们定义以下0结点，0结点代表结点没有键值，但是不代表没有孩子（注意NULL也视为有一个小孩），什么意思呢？看下面的图示

 2-3树中删除的注意事项

1、通过将delete结点从叶子结点向根结点移动，不断地判断delete结点的父兄结点符合哪种状况，如此递归下去，直到找到问题的出口并return，

2、注意当delete的父结点是NULL，那么树逆生长（树的高度-1），这就是2-3树的逆生长（即高度降低）一定使发生在根结点，而不是叶子结点

3、在结点的融合过程中，时刻注意更新每个结点的信息，包括结点类型，结点值，结点的父结点以及子结点

结尾：

作为最简单的B树，2-3树的实现仍然很繁琐，2-3-4树就更加麻烦了，且创建一颗2-3(-4)树的效率可能不尽如人意，而且红黑树作为2-3(-4)树的变种，红黑树的插入和删除更高效快捷，那么理解并且用代码实现2-3树似乎不重要了，但是理解2-3树对理解红黑树是有很大的帮助的，红黑树中的插入情况可以和2-3树中的插入、删除情况有所区别，但区别不大。

本人的2-3树代码太冗长了，就不发出来了。