跨模态哈希综述(更新中)
基于哈希变换跨模态方法综述
- 概要
-
- 有关本文
- 本方向在做什么事情
- 方法的提出与完善
-
- 局部敏感哈希LSH(1998)
- 谱哈希SH(NIPS '08)
- 多视图哈希CVH(IJCAI '11)
- 迭代量化哈希ITQ(TPAMI '12)与锚点图哈希AGH方法(ICML '11)
- 潜在语义稀疏哈希LSSH(SIGIR '14)
- 集合矩阵分解CMFH(CVPR '14)
- 语义保存哈希SePH(CVPR '15)
- 离散跨模态哈希DCH(TIP '17)
- 矩阵分解的有监督哈希SMFH(TIP '16)
- 可扩展的跨模态检索离散矩阵分解散列SCRATCH(MM '18/TCSVT '19)
- 基于融合相似性的哈希学习FSH(CVPR '17)
- 离散潜在因子哈希DLFH(TIP '19)
- DOCH(PR '22)
- FCMH(TCYB '22)
- DJSAH(TCSVP '22)
- ASFOH(TCYB '23)
- 公式推导
-
- 一个工具:
- 矩阵分解推导范例
- t-SNE算法
- DCC in SDH:
- SVT算法
概要
有关本文
本文将综述浅层跨模态检索方法的相关研究,以及具体研究的思想以及其进步性。其中关注的浅层跨模态方法主要分两类,第一类是基于矩阵分解的跨模态方法(Matrix Factorization);第二类是基于谱方法的跨模态方法(Spectral-based Hashing),这两类的研究是本文作者关注较多的浅层跨模态方法。
从整体的讲,跨模态检索方法有基于浅层的机器学习方法,也有基于深度学习的算法。深度学习的方法在检索的效果上有一定的优势,且可以直接对原始数据进行操作,但是相比于浅层模型,深度学习方法非常耗时,且不能够解释其目标函数,在大规模数据集上效率很低。本文关注浅层的哈希算法
本方向在做什么事情
无论浅层还是深层,跨模态检索的目的都是跨域语义鸿沟,即不同模态下,对某个事物存在的不同表示,比如描述一个人,用一段话描述和一张图片描述,所能够表达的信息是不同的,在不同的表示下,我们如果需要做到相互的检索,就需要从中分析出相同或相近的特征或语义,而这一步就是跨越语义鸿沟。不同的研究方法对于跨越语义鸿沟给出了不同的方法,而本综述中的跨越语义鸿沟的方法是需求一种映射关系,将不同模态的数据特征映射到一个共同的子空间,也叫子空间学习法或binary表示学习,将不同的数据模态映射到一个公共的汉明空间(Hamming Space),通过汉明距离(Hamming Distance)来检索。这种方式的优点是搜索性能很强,检索速度非常快,但是可能会带来信息损失,01编码会带来量化损失(quantization error)。很多研究也是基于如何优化这些浅层算法存在的问题而展开的,后文将详细阐述。
此外,跨模态方法还有有无监督之分,现阶段有监督的跨模态检索方法比无监督方法的检索效果要强,本文重点关注的方向的方法均为有监督方法,数据集中都有标签监督信息来辅助训练,但是早期的研究由于数据集的缺失等各种原因,大部分都是无监督方法,但是这些方法中的思想对于新的模型构建以及整个领域的发展都起着很关键的作用
方法的提出与完善
局部敏感哈希LSH(1998)
局部敏感哈希(Latent Semantic Hashing)为所有的跨模态哈希方法提供了思想基础,和传统的哈希避免碰撞,完成分类的思想不同,局部敏感哈希的目的就是产生碰撞,从而获取相似的内容。局部敏感哈希最开始主要应用于推荐系统领域,但推荐系统和跨模态检索解决的问题都是类似的检索问题,所以逐渐的,LSH也的思想也应用在了跨模态检索中。在LSH前,经历了NN到ANN再到LSH的过程,对于两个最近邻方法,本文不赘述
谱哈希SH(NIPS '08)
谱哈希(Spectral Hashing)是基于谱聚类的哈希方法的奠基作,将谱聚类思想引入到信息检索中。
谱哈希的方法还没有进入到跨模态的阶段,而是解决快速检索相似图像的问题。本文提出了可以通过编码后计算汉明距离来进行检索,并且对哈希函数提出了基本的要求。
首先对于哈希码,作者花了一定篇幅证明了,如果要优化一个最佳的二进制码,即使是只优化其中的某一个位,也是一个NP难问题,所以如何将问题简化是这篇文章算法的重点。本文提出了两个重要思想,首先是提出了一个优化函数的松弛版本,即消除对哈希码 { − 1 , 1 } \{-1,1\} {−1,1}的约束,将其去离散化;
而解决这个问题用到了拉格朗日算子的思想:
首先, Y Y Y是一个 n × k n\times k n×k的矩阵,其中 n n n是样本的数量, k k k是我们要保留的特征数量。 D D D是一个 n × n n\times n n×n的对角矩阵,其对角线元素为样本的度数, W W W是 n × n n\times n n×n的邻接矩阵。
我们的目标是求出如下式子的最小值:
t r a c e ( Y T ( D − W ) Y ) \mathrm{trace}(Y^T(D-W)Y) trace(YT(D−W)Y)
为了求解这个问题,我们可以使用拉格朗日乘子法。具体来说,我们可以将约束条件 Y T Y = I Y^TY = I YTY=I加入到目标函数中,形成一个带有拉格朗日乘子的新目标函数,即:
L ( Y , Λ ) = t r a c e ( Y T ( D − W ) Y ) + t r a c e ( Λ ( Y T Y − I ) ) \mathrm{L}(Y, \Lambda) = \mathrm{trace}(Y^T(D-W)Y) + \mathrm{trace}(\Lambda(Y^TY - I)) L(Y,Λ)=trace(YT(D−W)Y)+trace(Λ(YTY−I))
其中, Λ \Lambda Λ是一个 k × k k\times k k×k的拉格朗日乘子矩阵, I I I是一个 k × k k\times k k×k的单位矩阵。我们要对 Y Y Y求偏导数,并令其等于 0 0 0:
∂ L ∂ Y = 2 ( D − W ) Y + 2 Λ Y = 0 \frac{\partial \mathrm{L}}{\partial Y}=2(D-W)Y+2\Lambda Y=0 ∂Y∂L=2(D−W)Y+2ΛY=0
将上式改写为:
( D − W ) Y = Y Λ (D-W)Y=Y\Lambda (D−W)Y=YΛ
这是一个特征值问题,矩阵 D − W D-W D−W的特征向量组成的矩阵 Y Y Y和特征值组成的对角矩阵 Λ \Lambda Λ满足上式。因此, Y Y Y的列向量就是 D − W D-W D−W的 k k k个特征向量,对应的特征值就是 Λ \Lambda Λ的对角线元素。
最终,我们得到的 Y Y Y的解是 D − W D-W D−W的 k k k个特征向量。
谱哈希的在跨模态中的应用是很局限的:要求数据集是separable的,每个位的特征和其他位不相关,这是一种很理想的情况。
多视图哈希CVH(IJCAI '11)
多视图哈希(Cross-View Hashing)是谱哈希的多视图扩展,为后续的哈希方法提供了最初的数学框架以及优化算法,为优化的NP难问题提供了新的思路,被后续研究广泛引用。虽然本文的研究内容是有关多视图的,但是多模态和多视图中,将不同的视图的特征映射到相同汉明空间的思想和将不同模态数据的特征映射到共同汉明空间的思想是相同的,所以在早期的研究中,CVH也被作为一个跨模态检索的baseline。CVH基于子空间学习的思想,提出了优化函数
d i j = ∑ k = 1 K d ( y i ( k ) , y j ( k ) ) + ∑ k = 1 K ∑ k ′ > k K d ( y i ( k ) , y j ( k ′ ) ) m i n i m i z e : d ‾ = ∑ i = 1 n ∑ j = 1 n W i j d i j s u b j e c t t o : Y ( k ) e = 0 , 1 n Y ( k ) Y ( k ) T = I d , Y i j ( k ) ∈ { − 1 , 1 } f o r k = 1 , . . . , K d_{ij}=\sum_{k=1}^Kd(y_i^{(k)},y_j^{(k)})+\sum_{k=1}^K\sum_{k'>k}^Kd(y_i^{(k)},y_j^{(k')}) \\ \qquad\\ minimize: \overline d = \sum_{i=1}^{n}\sum_{j=1}^nW_{ij}d_{ij}\\ subject\space to: Y^{(k)}e= 0,\qquad \frac1nY^{(k)}{Y^{(k)}}^T = I_d,\qquad Y_{ij}^{(k)}\in\{-1,1\}\\ for\quad k = 1,...,K dij=k=1∑Kd(yi(k),yj(k))+k=1∑Kk′>k∑Kd(yi(k),yj(k′))minimize:d=i=1∑nj=1∑nWijdijsubject to:Y(k)e=0,n1Y(k)Y(k)T=Id,Yij(k)∈{−1,1}fork=1,...,K
其中 W W W是实例间的相似矩阵
但是这个目标函数是NP难问题(当K=1时退化为单模态,而SH中证明了该情况的优化是NP-hard)。本文提出嵌入 y i ( k ) y_i^{(k)} yi(k)和 x i ( k ) x_i^{(k)} xi(k)线性关系 y i ( k ) = A ( k ) T x i ( k ) y_i^{(k)}={A^{(k)}}^Tx_i^{(k)} yi(k)=A(k)Txi(k),让上述优化问题的求解变为了多项式的复杂度。(这篇文章提出了这个方法后并没有给出具体的闭式解的,但是给了一个闭式解的求解方法的论文引用,由于没有baseline,实验数量和内容都较少)
迭代量化哈希ITQ(TPAMI '12)与锚点图哈希AGH方法(ICML '11)
这两篇的内容不在本文中详细阐述,因为都不是直接的跨模态哈希方法,均是图哈希方法。
ITQ(Iterative Quantization: A Procrustean Approach to Learning Binary Codes for Large-Scale Image Retrieval)将谱哈希中对于主成分的处理进行了改进,谱哈希的思想是将方差最大的成分分配更多的bit,而ITQ的思想则是通过旋转矩阵使不同特征的分布方差接近。而文中论证了,这样做可以降低由于松弛带来的量化误差,所以通过优化出最优的旋转矩阵,可以得到最优的哈希码。ITQ方法增加了一个新的优化目标来对模型进行了改进,而正交旋转矩阵的引入也被后续的研究广泛引用。文中也提出了求解最优旋转矩阵的优化方法,通过迭代 B = s g n ( R V ) , P Ω Q = B V ′ , R = Q P ′ B= sgn(RV), P\Omega Q=BV',R=QP' B=sgn(RV),PΩQ=BV′,R=QP′来实现对B和R矩阵的学习。
AGH(Anchor Graph Hashing)是在Hashing with Graphs一文中,提出的一个基于锚点的数据间关系表示法,可以通过锚点构建的一个近似的邻接矩阵(如将其属于的聚类中心的距离来表示)来近似原本的一些方法中直接表示图片之间相似度的邻接矩阵,这样做可以很显著的提高效率。通过锚点来实现大数据集的简化,也在后续的文章中会有所体现。
潜在语义稀疏哈希LSSH(SIGIR '14)
潜在语义稀疏哈希(Latent Semantic Sparse Hashing for Cross-Modal Similarity Search)是最经典的跨模态哈希方法的基线方法。这篇文章和前面的方法最大的不同就是真正的实现了“跨模态”——提出了共同的潜在语义空间(latent semantic space)
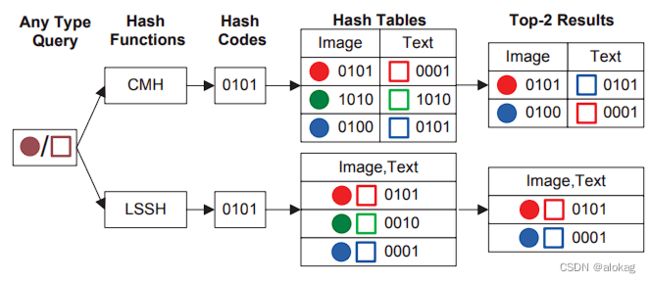
如上图所示,前面几种哈希编码方法均是针对单个模态的,而不同模态的数据集有不同的哈希码。LSSH认为,不同模态的数据存在潜在的语义关联,所以学习的哈希码应该在一个共同的汉明空间中。而这样的共同子空间的学习,可以很直接的实现跨模态的检索(搜索时间和占用的空间均削减到一半一下)。
LSSH的思想是,先将模态数据投影到其潜在语义空间,再将潜在语义空间内容投影到一个抽象的公共空间。
第一步投影 P I : R m → S I M , P T : R d → S T D \mathcal P_I:\mathbb R^m \rightarrow \mathcal S_I^M,\quad\mathcal P_T:\mathbb R^d \rightarrow\mathcal S_T^D PI:Rm→SIM,PT:Rd→STD
第二步投影到公共空间 R I : S I M → A k , R T : S T D → A k \textbf R_I:\mathcal S_I^M \rightarrow \mathcal A^k,\quad\textbf R_T:\mathcal S_T^D \rightarrow\mathcal A^k RI:SIM→Ak,RT:STD→Ak
类似构建了一个两层网络,将两种不同模态的数据变换到同一个空间下的同一组编码上。
即 R I P I ( x i ) = R T P T ( y i ) , ∀ i \textbf R_I\mathcal P_I(x_i)=\textbf R_T\mathcal P_T(y_i), \quad\forall i RIPI(xi)=RTPT(yi),∀i
最终这个共同空间可以被量化方法表示为一个共同编码集 H k \mathcal H^k Hk
LSSH由于还是无监督方法,所以潜在语义空间需要通过对模态单独处理来获取,这个问题在引入监督信息后被简化。LSSH中,图像模态的处理基于稀疏编码,而文本模态采用了一般矩阵分解方法来学习。关于稀疏编码的内容参考SLEP方法进行优化。
集合矩阵分解CMFH(CVPR '14)
(CSDN编辑器吃我内容真的吐了,写了两天的这个没了,重写一遍可能之前有些我认为的细节会没有掉)
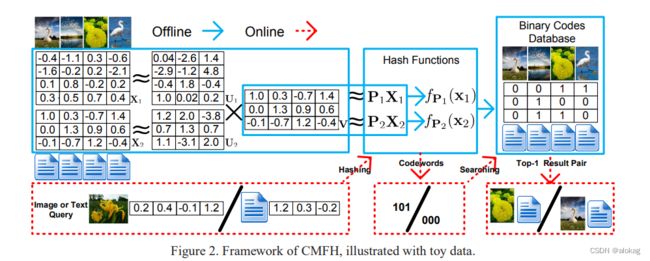
集合矩阵分解(Collective Matrix Factorization Hashing for Multimodal Data )是一个框架非常简单,基于矩阵分解的跨模态方法。文中提出了两个重要的假设,后续很多的研究如SCRATCH等,都是基于该文章中的这两个假设来进行的:
1.相关联的两个模态数据应该具有相同的潜在语义表示
2.这种相同的潜在语义表示可以变投影变成相同的二进制码,如 y = s i g n ( v ) y = sign\bf(v) y=sign(v)
基于两个假设,提出了潜在语义空间和原本模态数据之间存在一个投影,该投影为带有偏置的线性变换,偏置将二进制码变为0均值,作者提出这样可以让二进制码保存最多的信息,但是在构建优化函数的时候,作者似乎把这个偏置项给消除掉了,最终学习的内容变成了潜在语义信息空间和原本数据集空间的相互映射关系。
优化函数如下:
G = λ ∥ X ( 1 ) − U 1 V ∥ F 2 + ( 1 − λ ) ∥ X ( 1 ) − U 1 V ∥ F 2 + μ ( ∥ V − P 1 X ( 1 ) ∥ F 2 + ∥ V − P 2 X ( 2 ) ∥ F 2 ) + γ R G = \lambda \Vert \textbf X^{(1)}-\textbf U_1\textbf V\Vert_F^2+ (1-\lambda )\Vert \textbf X^{(1)}-\textbf U_1\textbf V\Vert_F^2\\+\mu(\Vert\textbf V- \textbf P_1\textbf X^{(1)}\Vert_F^2+ \Vert\textbf V- \textbf P_2\textbf X^{(2)}\Vert_F^2)+\gamma\bf R G=λ∥X(1)−U1V∥F2+(1−λ)∥X(1)−U1V∥F2+μ(∥V−P1X(1)∥F2+∥V−P2X(2)∥F2)+γR
R为正则项
本文的优化过程非常非常简单,最终的潜在语义空间直接通过符号可以映射为哈希码。以公式9为例,矩阵推导见后文公式推导部分,后续很多基于矩阵分解的方法中公式推导都遵循该部分的过程(这是个数学层面的问题,但是我线代学的不行这部分还是推了一段时间的)大体就是范数变为迹,再对迹拆分成各个子式,对子式求导求和
.
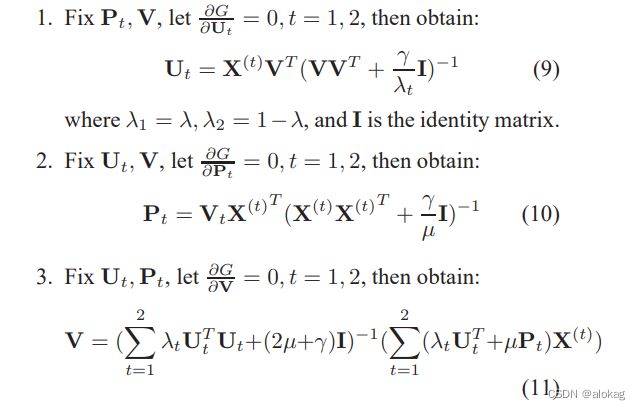
学到的 V 通过 B =sign( V ) \textbf V通过\text{\textbf B =sign(\textbf V)} V通过B =sign(V)转化为最终的哈希码。CMFH同样存在很多问题以及进步空间,但是他提供的优化策略是最简单且最清晰的。
语义保存哈希SePH(CVPR '15)
语义保存哈希(Semantics-Preserving Hashing for Cross-View Retrieval)也是一个将语义信息提取并应用到跨模态检索中的基线方法。
SePH中提出了两种概率分布,第一种有关数据本身语义相关性的概率分布,不同于前文中几种方法构建的“相似矩阵”,本文将其用概率分布来表示。表示为 P \mathcal P P;第二种概率分布,是最终生成的哈希码的概率分布,通过汉明距离来刻画相关性,本文对此采用了t-SNE方法,具体内容再公式推导部分,该概率分布表示为 Q \mathcal Q Q,其中 p i , j = A i , j ∑ k ≠ m A k , m , q i , j = ( 1 + h ( H i , H j ) ) − 1 ∑ k ≠ m ( 1 + h ( H k , H m ) ) − 1 p_{i,j} = \frac{A_{i,j}}{\sum_{k\neq m}A_{k,m}},\qquad q_{i,j}=\frac{(1+h(H_i,H_j))^{-1}}{\sum_{k\neq m}(1+h(H_k,H_m))^{-1}} pi,j=∑k=mAk,mAi,j,qi,j=∑k=m(1+h(Hk,Hm))−1(1+h(Hi,Hj))−1
其中h表示i实例和j实例的哈希码之间的汉明距离
参考t-SNE,需要最小化 P \mathcal P P和 Q \mathcal Q Q之间的KL-散度,于是可以构建出目标函数为
Ψ = min H ^ ∈ R n × d c ∑ i ≠ j p i , j log p i , j q i , j + α C ∥ ∣ H ^ ∣ − I ∥ 2 2 \Psi = \min_{\hat H\in\mathbb R^{n\times d_c}}\sum_{i\neq j} p_{i,j} \log \frac{p_{i,j}}{q_{i,j}}+\frac\alpha C\Vert\vert\hat H\vert - \textbf I \Vert_2^2 Ψ=H^∈Rn×dcmini=j∑pi,jlogqi,jpi,j+Cα∥∣H^∣−I∥22
其中 H ^ \hat H H^表示的是在连续域上的哈希码,即在 ( − 1 , 1 ) (-1,1) (−1,1)内的哈希码。该优化函数为非凸的,所以通过局部的优化来实现整体的优化,本文中采用的是梯度下降的方法来学习哈希码,具体求导略。
在SePH中哈希码学习和哈希函数的学习是分开的,是一个典型的两阶段的跨模态哈希方法,作者将哈希函数的学习视为一个在每个哈希码位上的二分类问题,所以可以用许多种方法(如线性回归,SVM和logistic回归等)本文采用的是核化的logistic回归,核函数核化可以让原本的数据在不容易被线性可分的情况下使特征升维,使其线性可分,从而完成哈希函数的学习,每一个模态中的哈希函数独立。
每一位 k k k都有
Θ = min w ( k ) ∑ i = 1 n log ( 1 + e − h i ( k ) ϕ ( X i ) w ( k ) ) + λ ∥ w ( k ) ∥ 2 2 \Theta = \min_{\textbf w^{(k)}}\sum_{i=1}^n\log(1+e^{-\textbf h_i^{(k)}\phi (X_i)\textbf w^{(k)}})+\lambda\Vert\textbf w^{(k)}\Vert_2^2 Θ=w(k)mini=1∑nlog(1+e−hi(k)ϕ(Xi)w(k))+λ∥w(k)∥22
其中 w ( k ) \textbf w^{(k)} w(k)是训练空间中的向量的线性组合,即 w ( k ) = Φ T v ( k ) \textbf w^{(k)} = \Phi^T\textbf v^{(k)} w(k)=ΦTv(k),其中 Φ \Phi Φ是核化特征矩阵。上式的计算量是很大的,所以本文提出选择 s s s个样本来进行计算。本文中对哈希码的计算是通过概率表示的,转化为哈希码的过程是比较+1位和-1位的概率大小。实验中,亲和矩阵用余弦相似矩阵替代,学习哈希函数采用了采样方法,采样采用了两种策略,第一种是k-means方法,第二种是随机采样,前者效果会略优。
离散跨模态哈希DCH(TIP '17)
DCH(Discrete Cross-modal Hashing)
这个方法的目标函数提出和CMFH的目标函数很接近,但由于标签监督信息的引入,所以将CMFH的目标函数中的前两项潜在语义学习的内容改成了标签监督信息学习。构建目标函数如下 G = ∥ Y − W T B ∥ F 2 + μ V ∥ B − P V T V ∥ F 2 + μ T ∥ B − P T T T ∥ F 2 ) + λ ∥ W ∥ F 2 G = \Vert\textbf Y-\textbf W^T\textbf B \Vert_F^2+\mu_V\Vert\textbf B- \textbf P_V^T\textbf V\Vert_F^2+\mu_T \Vert\textbf B- \textbf P_\text T^T\textbf T\Vert_F^2)+\lambda\Vert \textbf W\Vert_F^2 G=∥Y−WTB∥F2+μV∥B−PVTV∥F2+μT∥B−PTTT∥F2)+λ∥W∥F2

优化 W \bf W W和 Y \bf Y Y的方法是和之前方法相近的,但是优化 B \bf B B是NP-Hard的 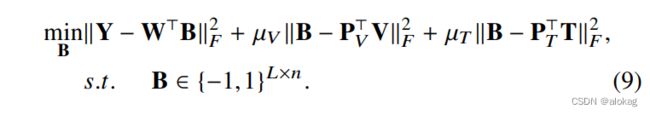
DCH给出的优化方案是逐位优化B,但这也导致了效率低的问题。优化B的方法参考了SDH(Supervised Discrete Hashing(CVPR '15))的方法,但论文里好像公式写错了。该方法采用DCC方法,先将无关项简化为一个辅助矩阵,然后进行拆分,不断将无关项常数化后,最后可以得到简化的解(但也有缺点,比如收敛较慢,以及有可能收敛到局部最优解等)。DCH强调了“Discrete”的概念,具体的来讲,就是在训练过程中保持着对每个变量的约束。如DCH中,为了保持 B ∈ { − 1 , 1 } \textbf {B} \in \{-1,1\} B∈{−1,1}采用了逐位优化的方法。
矩阵分解的有监督哈希SMFH(TIP '16)
SMFH是基于CMFH的方法,其中还有一个SCMFH。
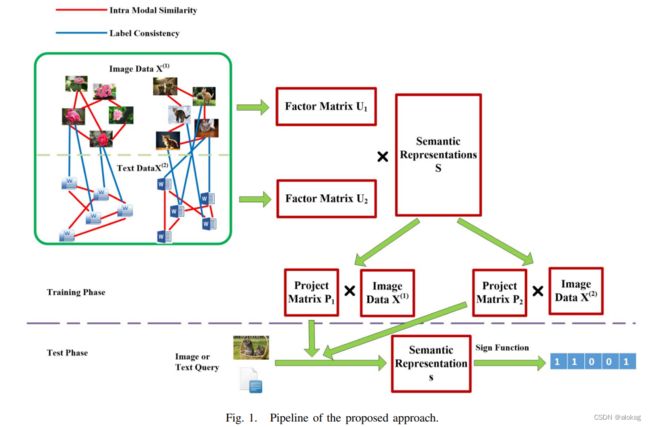
本文利用了标签信息来对潜在表示进行了学习,这个思路将监督信息成功的应用到了CMFH中。但是本文的优化方法存在一些问题。比如该方法不是离散的,用了松弛方法来进行优化,会导致量化损失。此外,优化用了拉格朗日矩阵,当方法应用于较大数据集的场景下会导致优化慢,作者提出用抽样的方法,但这也会导致信息损失。
可扩展的跨模态检索离散矩阵分解散列SCRATCH(MM '18/TCSVT '19)
可扩展的跨模态检索离散矩阵分解散列A Scalable Discrete Matrix Factorization Hashing for Cross-Modal Retrieval是前几种方法的结合


为什么引入旋转矩阵?旋转矩阵能够改变各个向量的方向并且不会改变向量的大小。它可以在训练期间保证优化问题离散,并直接产生离散的二进制码,可以避免一些大量化误差(这里引用了ITQ论文中“最优旋转矩阵可以降低量化误差”的思想)作者在此后又重申了一遍CMFH里面提到过的假设(这个地方不知道为什么要说是futher suppose)。用的是和CMFH里面一样的思路,将不同模态映射到相同潜在语义空间,表述为:
 不同模态的结构是非线性且难以分析出其规律的,但也不需要去了解其规律如何。将其处理为线性可分的,可以提升检索性能,所以将其进行核函数处理,不再利用原始的特征。将前面式子中出现的^(() ) 全部由(^(() ))替代以提高效果
不同模态的结构是非线性且难以分析出其规律的,但也不需要去了解其规律如何。将其处理为线性可分的,可以提升检索性能,所以将其进行核函数处理,不再利用原始的特征。将前面式子中出现的^(() ) 全部由(^(() ))替代以提高效果
无论是DJSAH还是SCRATCH,都用的是径向基函数的方法核化。核化后,所有的数据集的维度均由锚点数量决定,本文的实验中锚点选择为500个。所以图文特征矩阵均被转化为500维的特征。综合后有最终的目标函数:
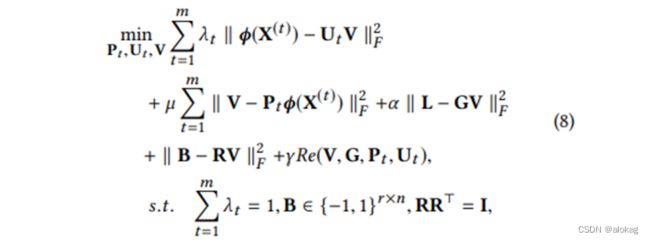
SCRATCH的结构简单,优化简单,且表现的效果很好,作为2018年的文章,在截至2023年的研究中依旧算是效果很好的模型。也像CMFH一样,成为很多后续研究的一个基本框架和对比对象,也是有监督的矩阵分解方法中最典型的方法之一。
基于融合相似性的哈希学习FSH(CVPR '17)
FSH(Cross-Modality Binary Code Learning via Fusion Similarity Hashing)是一个无监督方法,重点是提出了“fusion”的概念,简单的讲,就是许多此前的方法对不同模态的学习是通过自设参数来判断不同模态特征对语义的贡献程度(如 α ↔ 1 − α \alpha\leftrightarrow 1-\alpha α↔1−α),一些work很粗暴的设置为了 a l p h a = 0.5 alpha = 0.5 alpha=0.5。而本文提出了一个不同模态的融合的融合相似性,在双模态中,将 α \alpha α变为可学习的参数,这样模型可以更加稳定的在更多场景下应用,拓展到多模态则是设置为总和为n的权重参数集。
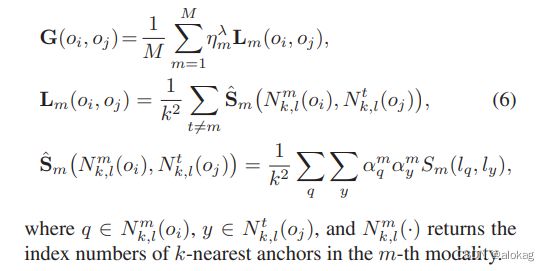
上图为融合相似性的构建,总体目标函数如下:
离散潜在因子哈希DLFH(TIP '19)
DLFH(Discrete Latent Factors Hashing] 可以看做是DCMH(Deep Cross Modal Hashing)的浅层方法版。但是虽然是浅层方法,但是其效率和效果都甚至更好。DCMH除了提出了基于深度学习的方法来进行哈希码生成外,还提出了一个最大化 UV \textbf{UV} UV相似度的思路。本文是基于该思路的浅层方法探索,负对数的似然函数定义如下,其中 Θ = U V T \Theta = \textbf U\textbf V^T Θ=UVT。和以往F范数最小化刻画相似性不同,DCMH采用了负对数似然,在本文中也一样。下式为优化目标函数。
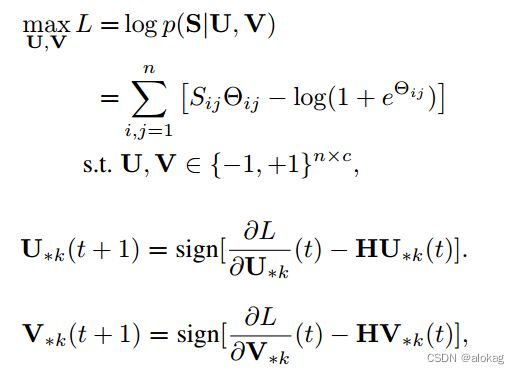
其中 p ( S|U,V ) = { σ ( Θ i j ) , S i j = 0 1 − σ ( Θ i j ) , S i j = 1 s . t . σ ( Θ i j ) = 1 1 − e − Θ i j p(\textbf {S|U,V})=\left\{ \begin{array}{lr}\sigma(\Theta_{ij}), &&S_{ij}=0\\ 1-\sigma(\Theta_{ij}),&&S_{ij}=1\end{array}\right.\qquad s.t.\quad\sigma(\Theta_{ij})=\frac 1{1-e^{-\Theta_{ij}}} p(S|U,V)={σ(Θij),1−σ(Θij),Sij=0Sij=1s.t.σ(Θij)=1−e−Θij1
本文提出了一个优化下界的最大值优化方法,首先将优化问题表示为二阶导形式,再通过二阶导的最小值替代二阶导来简化问题,达到了不错的优化效果
DOCH(PR '22)
FCMH(TCYB '22)
DJSAH(TCSVP '22)
ASFOH(TCYB '23)
公式推导
一个工具:
学长给了我一个很好的矩阵计算求导工具,叫做Matrix Calculus
矩阵分解推导范例
我们可以使用矩阵求导数的链式法则来计算 G G G关于 U U U的偏导数。我们有以下公式:
∂ ∂ U Tr ( A B ) = B T A T \frac{\partial}{\partial U}\text{Tr}(AB) = B^TA^T ∂U∂Tr(AB)=BTAT
∂ ∂ U Tr ( A A T ) = 2 A \frac{\partial}{\partial U}\text{Tr}(AA^T) = 2A ∂U∂Tr(AAT)=2A
∂ ∂ U Tr ( U X U T ) = X U + X T U \frac{\partial}{\partial U}\text{Tr}(UXU^T) = XU + X^TU ∂U∂Tr(UXUT)=XU+XTU
如果 f ( X ) = Tr ( A X ) f(X) = \text{Tr}(AX) f(X)=Tr(AX),其中 A A A是一个矩阵,那么 ∂ f ∂ X = A T \frac{\partial f}{\partial X} = A^T ∂X∂f=AT。
如果 f ( X ) = Tr ( A X B ) f(X) = \text{Tr}(AXB) f(X)=Tr(AXB),其中 A A A和 B B B是矩阵,那么 ∂ f ∂ X = A B T \frac{\partial f}{\partial X} = AB^T ∂X∂f=ABT。
要求解 G G G关于 U U U的偏导数为零的最优解,我们可以使用求导数的方法来解决这个问题。
要求解 G G G关于 U U U的偏导数,我们需要使用矩阵求导数的规则。我们首先展开 G G G的定义:
G = λ ∣ ∣ X − U V ∣ ∣ F 2 + γ ∣ ∣ U ∣ ∣ F 2 = λ Tr [ ( X − U V ) ( X − U V ) T ] + γ Tr ( U U T ) G=\lambda||X-UV||_F^2 + \gamma||U||_F^2=\lambda\text{Tr}[(X-UV)(X-UV)^T]+\gamma\text{Tr}(UU^T) G=λ∣∣X−UV∣∣F2+γ∣∣U∣∣F2=λTr[(X−UV)(X−UV)T]+γTr(UUT)
然后,我们将 G G G对 U U U求偏导数:
∂ G ∂ U = ∂ ∂ U ( λ Tr [ ( X − U V ) ( X − U V ) T ] + γ Tr ( U U T ) ) \frac{\partial G}{\partial U} = \frac{\partial}{\partial U}\left(\lambda\text{Tr}[(X-UV)(X-UV)^T]+\gamma\text{Tr}(UU^T)\right) ∂U∂G=∂U∂(λTr[(X−UV)(X−UV)T]+γTr(UUT))
使用矩阵求导数的规则,我们可以将其拆分为两个部分:
∂ G ∂ U = ∂ ∂ U ( λ Tr ( X ( X − U V ) T − U V ( X − U V ) T ) + γ Tr ( U U T ) ) + 2 γ U \frac{\partial G}{\partial U} = \frac{\partial}{\partial U}\left(\lambda\text{Tr}(X(X-UV)^T-UV(X-UV)^T)+\gamma\text{Tr}(UU^T)\right)+2\gamma U ∂U∂G=∂U∂(λTr(X(X−UV)T−UV(X−UV)T)+γTr(UUT))+2γU
将第一个式子整理一下:
∂ G ∂ U = ∂ ∂ U ( 2 λ Tr ( − U V X T + U V ( U V ) T ) ) + 2 γ U = 2 λ ( U V V T − X V T ) + 2 γ U \frac{\partial G}{\partial U}=\frac{\partial }{\partial U}(2\lambda\text {Tr}(-UVX^T+UV(UV)^T))+2\gamma U\\=2\lambda(UVV^T-XV^T) + 2\gamma U ∂U∂G=∂U∂(2λTr(−UVXT+UV(UV)T))+2γU=2λ(UVVT−XVT)+2γU
将其设为零,得到:
λ ( U V V T − X V T ) + γ U = 0 \lambda(UVV^T-XV^T) + \gamma U = 0 λ(UVVT−XVT)+γU=0
移项并整理,得到:
( V V T + γ λ I ) U = X V (VV^T+\frac{\gamma}{\lambda}I)U = XV (VVT+λγI)U=XV
接下来,我们将左侧的矩阵求逆,得到:
U = X V T ( V V T + γ λ I ) − 1 U = XV^T(VV^T+\frac{\gamma}{\lambda}I)^{-1} U=XVT(VVT+λγI)−1
这就是 G G G关于 U U U的偏导数为零时的最优解。
t-SNE算法
假设我们有 n n n个高维数据点 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn,其中 x i ∈ R D x_i \in \mathbb{R}^D xi∈RD, D D D为数据的维度。我们要将这 n n n个数据点降维为 k k k维(通常为 k = 2 k=2 k=2或 k = 3 k=3 k=3),得到 n n n个低维数据点 y 1 , y 2 , . . . , y n y_1,y_2,...,y_n y1,y2,...,yn,其中 y i ∈ R k y_i \in \mathbb{R}^k yi∈Rk。
计算高维空间中的相似度:
对于数据点 x i x_i xi和 x j x_j xj,t-SNE使用高斯分布 p j ∣ i p_{j|i} pj∣i来表示在高维空间中, x i x_i xi选择 x j x_j xj作为它的邻居的概率,公式如下:
p j ∣ i = exp ( − ∥ x i − x j ∥ 2 / 2 σ i 2 ) ∑ k ≠ i exp ( − ∥ x i − x k ∥ 2 / 2 σ i 2 ) p_{j|i}=\frac{\exp(-\lVert x_i-x_j \rVert^2/2\sigma_i^2)}{\sum_{k\neq i}\exp(-\lVert x_i-x_k \rVert^2/2\sigma_i^2)} pj∣i=∑k=iexp(−∥xi−xk∥2/2σi2)exp(−∥xi−xj∥2/2σi2)
其中 σ i \sigma_i σi是高斯分布的方差,它可以根据数据点的密度来自适应地调整。通常情况下,我们可以将 σ i \sigma_i σi设置为所有点到其 k k k个最近邻点的距离的平均值。
计算低维空间中的相似度:
对于数据点 y i y_i yi和 y j y_j yj,t-SNE使用t分布 q j ∣ i q_{j|i} qj∣i来表示在低维空间中, y i y_i yi选择 y j y_j yj作为它的邻居的概率,公式如下:
q j ∣ i = ( 1 + ∥ y i − y j ∥ 2 ) − 1 ∑ k ≠ i ( 1 + ∥ y i − y k ∥ 2 ) − 1 q_{j|i}=\frac{(1+\lVert y_i-y_j \rVert^2)^{-1}}{\sum_{k\neq i}(1+\lVert y_i-y_k \rVert^2)^{-1}} qj∣i=∑k=i(1+∥yi−yk∥2)−1(1+∥yi−yj∥2)−1
其中 ( 1 + ∥ y i − y j ∥ 2 ) − 1 (1+\lVert y_i-y_j \rVert^2)^{-1} (1+∥yi−yj∥2)−1是t分布的形式,它使得远离 y i y_i yi的点在低维空间中的概率分布趋向于0。t分布的自由度为1,也就是说,它只有一个自由度。
最小化KL散度:
t-SNE的目标是最小化高维空间和低维空间之间的KL散度,公式如下:
KL ( P ∣ ∣ Q ) = ∑ i ∑ j p j ∣ i log p j ∣ i q j ∣ i \text{KL}(P||Q)=\sum_i\sum_j p_{j|i} \log \frac{p_{j|i}}{q_{j|i}} KL(P∣∣Q)=i∑j∑pj∣ilogqj∣ipj∣i
使用梯度下降方法最小化上述目标函数,即可得到最终的低维嵌入 y 1 , y 2 , . . . , y n y_1,y_2,...,y_n y1,y2,...,yn。
DCC in SDH:
SVT算法
Singular value thresholding (SVT) algorithm是一种矩阵优化算法,用于处理矩阵的低秩近似问题。该算法通常用于矩阵补全、矩阵降噪、矩阵压缩等领域。
在低秩近似问题中,给定一个矩阵 A A A,目标是找到一个秩为 r r r 的矩阵 X X X,使得 X X X 与 A A A 的差异最小。其中, r r r 是矩阵的秩,通常 r r r 远小于矩阵的行数和列数。
SVT算法的基本思想是:将矩阵 A A A 进行奇异值分解(SVD),得到矩阵 U Σ V T U\Sigma V^T UΣVT,其中 U U U 和 V V V 是正交矩阵, Σ \Sigma Σ 是对角矩阵,对角线上的元素是 A A A 的奇异值。然后,对 Σ \Sigma Σ 中的每个元素进行阈值处理,将小于阈值的元素置为0,大于等于阈值的元素保留,得到新的对角矩阵 Σ ′ \Sigma' Σ′. 最后,将 U Σ ′ V T U\Sigma'V^T UΣ′VT 作为 A A A 的近似矩阵,完成矩阵的低秩近似。
具体来说,给定矩阵 A A A,假设其奇异值分解为 A = U Σ V T A=U\Sigma V^T A=UΣVT,设阈值为 τ \tau τ,则SVT算法的迭代过程如下:
1.计算 A A A 的SVD: A = U Σ V T A=U\Sigma V^T A=UΣVT
2.将 Σ \Sigma Σ 中的每个元素进行阈值处理: Σ ′ i , i = { Σ i , i − τ , Σ i , i > τ 0 , ∣ Σ i , i ∣ ≤ τ Σ i , i + τ , Σ i , i < − τ \Sigma'{i,i} = \begin{cases} \Sigma{i,i}-\tau, \Sigma_{i,i}>\tau\ 0, |\Sigma_{i,i}|\leq\tau \ \Sigma_{i,i}+\tau, \Sigma_{i,i}<-\tau\end{cases} Σ′i,i={Σi,i−τ,Σi,i>τ 0,∣Σi,i∣≤τ Σi,i+τ,Σi,i<−τ
3.得到近似矩阵: X = U Σ ′ V T X=U\Sigma'V^T X=UΣ′VT
4.检查 X X X 是否满足停止条件,如果满足,则返回 X X X,否则继续迭代。
SVT算法的停止条件可以是迭代次数、目标函数的收敛性等。该算法的优点是简单易实现,收敛速度较快。同时,由于奇异值分解的优良性质,SVT算法的近似矩阵具有较好的数学性质和性能。


