趣学算法学习笔记1
趣学算法学习笔记
问题 0-1 计算逆序数
问题描述
这个学期 Amy 开始学习一门重要课程——线性代数。学到行列式的时候,每次遇到对给定的序列计算其逆序数,她都觉得是个很闹心的事。所以,她央求她的好朋友 Ray 为她写一段程序,用来解决这样的问题。作为回报,她答应在周末舞会上让 Ray 成为她的伦巴舞舞伴。所谓序列 A 的逆序数,指的是序列中满足 i
输入
输输入文件包含若干个测试案例。每个案例的第一行仅含一个表示序列中元素个数的整数N(1≤N≤500000)。第二行含有 N 个用空格隔开的整数,表示序列中的 N 个元素。每个元素的值不超过 1 000 000 000。N=0 是输入数据结束的标志。
输出
每个案例仅输出一行,其中只有一个表示给定序列的逆序数整数
输入样例
3
1 2 3
2
2 1
0
输出样例
0
1
伪代码
打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取案例数据 N
while N>0
do 创建数组 A[1..N]
for i←1 to N
do 从 inputdata 中读取 A[i]
result←GET-THE-INVERSION(A)
将 result 作为一行写入 outputdata
从 inputdata 中读取案例数据 N
关闭 inputdata
关闭 outputdata
其中,第 8 行调用计算序列 A[1…N]的逆序数过程 GET-THE-INVERSION(A)是解决一个案例的关键,其伪代码过程如下。
GET-THE-INVERSION(A) A[1..N]表示一个序列
N←length[A]
count←0
for j←N downto 2
do for i←1 to j-1
do if A[i]>A[j] 检测到一个逆序
then count←count+1 累加到计数器
return count
算法 0-1 解决“计算逆序数”问题的一个案例的算法伪代码过程
cpp
#include 计数问题
累积计数法
这样的问题在实际中往往要通过几个步骤来解决,每个步骤都会产生部分数据,问题的目标是计算出所有步骤产生数据的总和。对这样的问题通常设置一个计数器(变量) ,然后依步骤(往往可以通过循环实现各步骤的操作)将部分数据累加到计数器,最终得到数据总和。
问题 1-1 骑士的金币
问题描述
国王用金币赏赐忠于他的骑士。骑士在就职的第一天得到一枚金币。接下来的两天(第二天和第三天)每天得到两枚金币。接下来的三天(第四、五、六天)每天得到三枚金币。接下来的四天(第七、八、九、十天)每天得到四枚金币。这样的赏赐形式一直延续:即连续 N 天骑士每天都得到 N 枚金币后,连续 N+1 天每天都将得到 N+1枚金币,其中 N 为任一正整数。编写一个程序,对给定的天数计算出骑士得到的金币总数(从任职的第一天开始)。
编写一个程序,对给定的天数计算出骑士得到的金币总数(从任职的第一天开始)。
输入
输入文件至少包含一行,至多包含 21 行。输入中的每一行(除最后一行)表示一个测试案例,其中仅含一个表示天数的正整数。天数的取值范围为 1~10000。输入的最后一行仅含整数 0,表示输入的结束。
输出
对输入中的每一个测试案例,恰好输出一行数据。其中包含两个用空格隔开的正整数,前者表示案例中的天数,后者表示骑士从第一天到指定的天数所得到的金币总数。
输入样例
10
6
7
11
15
16
100
10000
1000
21
22
0
输出样例
10 30
6 14
7 18
11 35
15 55
16 61
100 945
10000 942820
1000 29820
21 91
22 98
解题思路
(1)数据的输入与输出
根据题面对输入数据格式的描述,我们知道输入文件中包含多个测试案例,每个测试案例的数据仅占一行,且仅含一个表示骑士任职天数的正整数 N。N=0 是输入结束标志。对于每个案例,计算所得结果为国王赐予骑士的金币数,作为一行输出到文件。按此描述,我们可以用下列过程来读取数据,处理后输出数据。
打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取案例数据 N
while N>0
do result←GOLDEN-COINS(N)
将"N result"作为一行写入 outputdata
从 inputdata 中读取案例数据 N
关闭 inputdata
关闭 outpudata
其中,第 5 行调用计算骑士执勤 N 天能得到金币数的过程 GOLDEN-COINS(N)是解决
一个案例的关键。
GOLDEN-COINS(N)
coins←0, k←1, days←0
while days+k≤N
do coins←coins+k*k
days←days+k
k←k+1
j←N-days
coins←coins+k*j
return coins
算法 1-1 对已知的天数 N,计算从第 1 天到第 N 天总共所得金币数的过程
cpp
#include 问题 1-2 扑克牌魔术
问题描述
你能将一摞扑克牌在桌边悬挂多远?若有一张牌,你最多能将它的一半悬挂于桌边。若有两张牌,最上面的那张最多有一半伸出下面的那张牌,而底下的那块牌最多伸出桌面三分之一。因此两张牌悬挂于桌边的总长度为 1/2 + 1/3 = 5/6。。一般地,对 n 张牌伸出桌面的长度为 1/2 + 1/3 + 1/4 + … 1/(n + 1),其中最上面的那块牌伸出其下的牌 1/2,第二块牌伸出其下的那块牌 1/3,第三块牌伸出其下的那块牌 1/4,以此类推,最后那块牌伸出桌面 1/(n+1)。如图 1-1 所示。
输入
输入包含若干个测试案例,每个案例占一行。每行数据包含一个有两位小数的浮点数 c,取值于[0.01, 5.20]。最后一行中 c 为 0.00,表示输入文件的结束.
输出
对每个测试案例,输出能达到悬挂长度为 c 的最少的牌的张数。需按输出样例的格式输出。
输入样例
1.00
3.71
0.04
5.19
0.00
输出样例
3 card(s)
61 card(s)
1 card(s)
273 card(s)
解题思路
(1)数据的输入与输出
根据题面描述,输入文件的格式与问题 1-1 的相似,含有多个测试案例,每个案例占一行数据,其中包含表示扑克牌悬挂于桌边的总长度的数据 c 。 。c=0.0 是输入数据结束的标志。对每个案例数据 c 进行处理,计算所得的结果为能悬挂于桌边的总长度为 c 的扑克牌的张数,按格式“张数 card(s)”作为一行输出文件。
打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取案例数据 c
while c≠0.0
do result← HANGOVER(c)
将"result card(s) "作为一行写入 outputdata
从 inputdata 中读取案例数据 c
关闭 inputdata
关闭 outpudata
其中,第 5 行调用计算能悬挂在桌边的长度为 c 的扑克牌张数的过程 HANGOVER©是解决一个案例的关键.
(2)处理一个案例的算法过程
HANGOVER(c)
n←1, length←0
while length<c
do length←length+1/(n+1)
n←n+1
if length>c
then n←n-1
return n
算法 1-2 对已知的纸牌悬挂长度 c,计算纸牌张数的过程
算法中,第 1 行设置了两个计数器: n(初始化为 1)和 length(初始化为 0)分别表示扑克牌张数和悬挂在桌边的长度。。第 2~4 行的 while 循环的重复执行条件是 length< c,每次重复将 1/(n+1)累加到 length,且 n 自增 1。该循环结束时必有 length≥c(等价地,意味着 n是第 1 个使得该条件成立的纸牌数)。若 length>c,则意味着 n 应当减少 1(这就是第 5~6行的功能)。
算法的运行时间依赖于第 2~4 行的 while 循环重复次数 n。由于
1 / 2 + 1 / 3 + ⋯ + 1 / n ⩽ 1 + 1 / 2 + 1 / 3 + ⋯ + 1 / ( 2 ⌈ n / 2 ⌉ − 1 ) = 1 + ( 1 / 2 + 1 / 3 ) + ( 1 / 2 2 + 1 / ( 2 2 + 2 ) + 1 / ( 2 2 + 3 ) ) + ⋯ + ( 1 / 2 i + 1 / ( 2 i + 1 ) + ⋯ + 1 / ( 2 i + 2 i − 1 ) ) + ⋯ + ( 1 / 2 lg n / 2 + 1 / ( 2 lg n / 2 + 1 ) + ⋯ + 1 / ( 2 lg n / 2 ⌉ + 2 lg n / 2 ⌉ − 1 ) ) < 1 + ( 1 / 2 + 1 / 2 ) + ( 1 / 2 2 + 1 / 2 2 + 1 / 2 2 + 1 / 2 2 ) + ⋯ + ( 1 / 2 i + 1 / 2 i + … + 1 / 2 i ⏟ 2 i ) + ⋯ + ( 1 / 2 lg [ n / 2 ⌉ + 1 / 2 lg [ n / 2 ⌉ ⏟ 2 lg [ n / 2 ] + … + 1 / 2 lg [ n / 2 ⌉ ) = 1 + 1 + … + 1 ⏟ ⌈ n / 2 ⌉ = Θ ( lg n ) \begin{array}{l} 1 / 2+1 / 3+\cdots+1 / n\\ \leqslant 1+1 / 2+1 / 3+\cdots+1 /(2\lceil n / 2\rceil-1)\\ =1+(1 / 2+1 / 3)+\left(1 / 2^{2}+1 /\left(2^{2}+2\right)+1 /\left(2^{2}+3\right)\right)+\cdots\\ +\left(1 / 2^{i}+1 /\left(2^{i}+1\right)+\cdots+1 /\left(2^{i}+2^{i}-1\right)\right)+\cdots\\ \left.+\left(1 / 2^{\lg n / 2}+1 /\left(2^{\lg n / 2}+1\right)+\cdots+1 /\left(2^{\lg n / 2}\right\rceil+2^{\lg n / 2\rceil}-1\right)\right)\\ <1+(1 / 2+1 / 2)+\left(1 / 2^{2}+1 / 2^{2}+1 / 2^{2}+1 / 2^{2}\right)+\cdots\\ +(\underbrace{1 / 2^{i}+1 / 2^{i}+\ldots+1 / 2^{i}}_{2^{i}})+\cdots\\ +(\underbrace{\left.1 / 2^{\lg [n / 2\rceil}+1 / 2^{\lg [n / 2}\right\rceil}_{2^{\lg }[n / 2]}+\ldots+1 / 2^{\lg [n / 2\rceil})\\ =\underbrace{1+1+\ldots+1}_{\lceil\mathrm{n} / 2\rceil}=\Theta(\lg n) \end{array} 1/2+1/3+⋯+1/n⩽1+1/2+1/3+⋯+1/(2⌈n/2⌉−1)=1+(1/2+1/3)+(1/22+1/(22+2)+1/(22+3))+⋯+(1/2i+1/(2i+1)+⋯+1/(2i+2i−1))+⋯+(1/2lgn/2+1/(2lgn/2+1)+⋯+1/(2lgn/2⌉+2lgn/2⌉−1))<1+(1/2+1/2)+(1/22+1/22+1/22+1/22)+⋯+(2i 1/2i+1/2i+…+1/2i)+⋯+(2lg[n/2] 1/2lg[n/2⌉+1/2lg[n/2⌉+…+1/2lg[n/2⌉)=⌈n/2⌉ 1+1+…+1=Θ(lgn)
即 c = Θ ( l g n ) c=Θ(lgn) c=Θ(lgn),亦即 n = Θ ( 2 c ) n=Θ(2^c) n=Θ(2c)。于是该算法的运行时间 T ( c ) = n = Θ ( 2 c ) T(c)=n=Θ(2^c) T(c)=n=Θ(2c)。幸好 c 介于 0.01~5.20之间,否则当 c 很大时,算法是极费时的。
#include 问题 1-3 能量转换
问题描述
魔法师百小度也有遇到难题的时候——现在,百小度正在一个古老的石门面前,石门上有一段古老的魔法文字,读懂这种魔法文字需要耗费大量的能量和脑力。过了许久,百小度终于读懂了魔法文字的含义:石门里面有一个石盘,魔法师需要通过魔法将这个石盘旋转 X 度,以使上面的刻纹与天相对应,才能打开石门。但是,旋转石盘需要 N 点能量值,而为了解读密文,百小度的能量值只剩 M 点了!破坏石门是不可能的,因为那将需要更多的能量。不过,幸运的是,作为魔法师的百小度可以耗费 V 点能量,使得自己的能量变为现在剩余能量的 K 倍(魔法师的世界你永远不懂,谁也不知道他是怎么做到的)。例如,现在百小度有 A 点能量,那么他可以使自己的能量变为(A-V)×K 点(能量在任何时候都不可以为负,即:如果 A 小于 V 的话,就不能够执行转换)。然而,在解读密文的过程中,百小度预支了他的智商,所以他现在不知道自己是否能够旋转石盘并打开石门,你能帮帮他吗?
输入
输入数据第一行是一个整数 T,表示包含 T 组测试案例。
接下来是 T 行数据,每行有 4 个自然数 N, M, V, K(字符含义见题目描述)。
数据范围如下:
T ≤ 100 T≤100 T≤100
N , M , V , K ≤ 1 0 8 N, M, V, K ≤ 10^8 N,M,V,K≤108
输出
对于每个测试案例,请输出最少做几次能量转换才能够有足够的能量点开门;如果无法做到,请直接输出“−1”。
输入样例
4
10 3 1 2
10 2 1 2
10 9 7 3
10 10 10000 0
解题思路
(1)数据的输入与输出
题面告诉我们,输入文件的第一行给出了测试案例的个数 T,其后的 T 行数据,每行表示一个案例,读取每个案例的输入数据 N, M, V, K,处理后得到的结果是能量转换次数(若经过若干次能量转换能够打开石门)或−1(不可能打开石门),并将所得结果作为一行写入输出文件。表示成伪代码过程如下。
打开输入文件 inputdata创建输出文件 outputdata从 inputdata 中读取案例数 Tfor t←1 to T do 从 inputdata 中读取案例数据 N, M, V, K result← ENERGY-CONVERSION(N, M, V, K) 将 result 作为一行写入 outputdata 中关闭 inputdata关闭 outpudata
(2)处理一个案例的算法过程
对于问题输入中的一个案例数据 N, M, V, K,需考虑两个特殊情况:
1 M ≥N,即百小度一开始就具有足够的能量打开石门。此时,百小度立刻打开石门。
2 M 一般情况下,(即 M< N 且 M≥ V ),从 A = M 开始,模拟百小度反复转换能量 A←(A -V )×K 设置跟踪转换能量的次数的计数器 count ,直至能量足以打开石门为止(即 A≥N ),), count 即为所求。在这一过程中,需要监测能量转换 A←( A− V)×K 是否增大了能量 A,如果检测到某次转换后 A≥ (A−V)×K,那意味着从此不可能增大能量,所以在这种情况下百小度也不能打开石门。 将上述思考写成伪代码如下。 算法 1-3 对一个案例数据 N, M, V, K,计算最少能量转换次数的过程 算法 1-3 中,第 1、12 行耗时为常数。。第 2~3 行和第 4~5 行的 if 结构也都是常数时间的操作。第 6~11 行的 repeat-until 结构,A 从 M 开始,循环条件是 A≥N,每次重复第 9行将使 A 至少增加 1,所以至多重复 N-M 次。因此,过程ENERGY-CONVERSION 的运行时间为 O(N-M)。 cpp 牛妞 Betsy 绕着谷仓闲逛时,发现农夫 John 建了一个秘密的暖房,里面培育了各种奇花异草,五彩缤纷。Betsy 惊喜万分,她的小牛脑瓜里顿时与暖房一样充满了各色的奇思妙想。“我要沿着农场篱笆挖上一排共 F(7≤F≤10000)个种花的坑。”Betsy 心里想着。“我要每 3 个坑(每隔 2 个坑)种一株每 7 个坑(每隔 6 个坑)种一株秋海棠,每 4 个坑(每隔 3 个坑)种一株雏菊…并且让这些花儿永远开放。”Betsy不知道如此栽种后还会留下多少个坑,但她知道这个数目取决于每种花从哪一个坑开始,每N 个坑栽种一株 我们来帮 Betsy 计算出会留下多少个坑可以栽种其他的花。共有 K (1≤K≤100)种花,每种花从第 L (1≤L≤F)个坑开始,每隔 I-1 个坑占据一个坑。。计算全部栽种完成后剩下的未曾占用的坑。 按 Betsy 的想法,她可以将种植计划描述如下: 30 3 [30 个坑;3 种不同的花] 1 3 [从第 1 个坑开始,每 3 个坑种一株玫瑰] 3 7 [从第 3 个坑开始,每 7 个坑种一株秋海棠] 1 4 [从第 1 个坑开始,每 4 个坑种一株雏菊] 于是,花园中篱笆前开始时那一排空的坑形状如下: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 种上玫瑰后形状如下: R . . R . . R . . R . . R . . R . . R . . R . . R . . R . . 种上秋海棠后形状如下: R . B R . . R . . R . . R . . R B . R . . R . B R . . R . . 种上雏菊后形状如下: R . B R D . R . D R . . R . . R B . R . D R . B R . . R D . 留下 13 个尚未栽种任何花的坑。 输入 第 1 行:两个用空格隔开的整数 F 和 K。 第 2~K+1 行:每行包含两个用空格隔开的整数 Lj 和 Ij,表示一种花开始栽种的位置和间隔。 输出 仅含一行,只有一个表示栽种完毕后剩下的空坑数目的整数。 输入样例 30 3 输出样例 13 解题思路 (1)数据的输入与输出 本问题的输入仅含一个测试案例。输入的开头是表示栽种花的坑数目和栽种花的种数的两个数 F 和 K。案例中还包含两个序列:每种花的栽种起始位置 L[1…K]和栽种间隔 I[1…K]。读取这些数据,处理计算出栽种完所有 K 种花后, F 个坑中还剩多少个是空的,并把结果作为一行数据写入输出文件中。 其中,第 7 行调用过程 THE-FLOWER-GARDEN(F, K, L, I)计算 Betsy 在篱笆前将 K 种花按计划裁种完毕还剩下的空坑数目是解决这个案例的关键。 (2)处理这个案例的算法过程 对于一个测试案例,设 K 种花中开始栽种位置最小的坑的编号为 i,设置一个空坑计数器 count,初始化为 i-1,因为在 i 之前的坑必不会载上任何花。从当前位置开始依次考察每一个坑是否会栽上一株花。如果 K 种花按计划都不会占据这个坑,则 count 自增 1。所有的位置考察完毕,累加在 count 中的数据即为所求。 算法 1-4 对一个案例数据 F, K, L, I,计算剩下空坑数目的过程 cpp 问题描述 一年一度的百度之星大赛又开始了,这次参赛人数创下了吉尼斯世界纪录。于是,百度之星决定奖励一部分人:所有资格赛提交 ID 以 x 结尾的参赛选手将得到精美礼品一份 小小度同学非常想得到这份礼品,于是他就连续提交了很多次,提交的 ID 从 a 连续到b。他想知道能得到多少份礼品,你能帮帮他吗? 输入 第一行一个正整数 T 表示测试案例数。接下来 T 行,每行 3 个不含多余前置零的整数$ x,a,b(0≤x≤10{18},1≤a≤b≤10{18})$。 输出 T 行。每行为对应的数据下,小小度得到的礼品数。 输入样例 2 88888 88888 88888 36 237 893 输出样例 1 解题思路 (1)数据的输入与输出 题面中告诉我们,输入文件的第一个数据指出了所含的测试案例数 T,每个案例的输入数据仅占一行,其中包含了 3 个分别表示 ID 尾数 x 、ID 取值下界 a 和上界 b 的整数。计算所得结果为 a~b 内能够得到礼物的 ID(尾数为 x)个数,作为一行输出到文件中。表示成伪代码如下。 其中,第 6 行调用过程 GIFT (x, a, b)计算能够得到的礼物数是解决一个案例的关键。 (2)处理一个案例的算法过程 对一个测试案例 x, a, b 而言,很容易想到用列举法穷尽 a~b 所有的整数,检测每一个的尾数是否与 x 相等。跟踪相等的个数: 算法 1-5 对一个测试案例数据 x, a, b,累加计算获得礼品数的算法过程 算法 1-5 中的第 1、2 行计算 m=10^t,其中 t 为 x 的 10 进制位数,可以用如下操作实现: 显然耗时为 l o g 10 x log_{10}x log10x,若 a~b 之间有 n 个数则上述算法中第 3~6 行代码的运行时间是 Θ ( n ) Θ(n) Θ(n),于是算法 1-5 的运行时间为 Θ ( l o g 10 x ) + Θ ( n ) Θ(log10x)+ Θ(n) Θ(log10x)+Θ(n)。借助数学计算,我们可以把解决这个问题的算法时间缩小为 Θ ( l o g 10 x ) Θ(log_{10}x) Θ(log10x)。 算法 1-6 对一个测试案例数据 x, a, b,直接计算获得礼品数的算法过程 cpp 问题描述 农夫 John 养了一群牛妞。有些牛妞很任性,时常离家出走。一天,John 得知了他的一头在外流浪的牛妞出后想立刻去把她领回家。John 从数轴上的点 N (0≤N≤100 000)处出发,牛妞出没于同一数轴上点 K (0≤K≤100 000)处。John 有两种移动方式:走路或远距飞跃。 走路:John 在一分钟内可从点 X 走到点 X-1 或点 X+1 处 远距飞跃:John 可以在一分钟内从任意点 X 处飞跃到点 2 X 处 假定牛妞对自身的危险一无所知,一直在原地溜达,John 最少要花多少时间才能够抓到她? 输入 输入文件的第一行仅含一个表示测试案例个数的整数 T。其后跟着 T 行数据,每行数据描述一个测试案例,包括两个用空格隔开的整数:N 和 K。 输出 每个案例只有一行输出:John 抓到牛妞的最少时间(分钟)。 输入样例 2 输出样例 4 解题思路 (1)数据的输入与输出 根据题面中对输入、输出数据的格式描述,我们可以将处理所有案例的过程表示如下。 cpp 描述 你是个暴脾气,最讨厌等待。你打算去新奥尔良拜访一位朋友。来到公交站你才发现这里的调度表是世界上最糟糕的。这个车站并没有列出各路公交车班车到达与出发的时间表,只列出各相邻班车的发车间隔时长. 暴躁的你从包中抓出平板电脑,试图写一段程序以计算最近来到的班车还需要等待多久。嘿,看来你只能这样了,不是吗? 输入 本问题的输入包含不超过 100 个测试案例。每个案例的输入数据格式如下。 一个测试案例的数据包括四个部分: 开头行——只有一行,“START N”,其中的 N 表示公交车路数(1≤N≤20)。 路线发车间隔区间行——共有 N 行。每行由 M(1≤M≤10)个发车间隔时长组成,这些数据表示这一路线的各班车上一班发车起到本班车出发时刻的间隔时间长度。每个间隔时长是一个介于 1~1000 之间的整数 到达时间——仅一行。该行数据表示你到达车站开始等待的时间。这个数据表示的是从当天车站开始运行到你来到车站的时间单位数(所有的线路的车都是从时间 0 开始运行的)。这是一个非负整数(若为 0,意味着班车在你到站时起步)结束行——单一的一行,“END”。最后一个测试案例后有一行“ENDOFINPUT”,作为输入结束标志 输出 对每一个测试案例,恰有一行输出。这一行仅包含一个表示你在下一趟班车到来之前需要等待的时间单位数。我们希望你等来的这班车是去往新奥尔良的! 注意 每班公交连续不断地循环运行于它的线路上。若乘客在班车离开时刻到达,他/她将搭上这班车。 输入样例 START 3 输出样例 200 描述成伪代码如下 其中,第 11 行调用过程 WORLD-WORST-BUS-SCHEDULE(durations, arrival)计算乘客最小的等车时间,是解决一个案例的关键。 (2)处理一个案例的算法过程 对一个案例而言,将各路车的出发间隔时长记录在一组数组 durations 中, d u r a t i o n s [ i ] [ l ] durations[i][l] durations[i][l]表示第 i 路车第 j 次发车距第 j-1 次发车的时间间隔。 T i = ∑ j = 1 m d u r a t i o n s [ i ] [ l ] T_i=\sum^m_{j=1}durations[i][l] Ti=∑j=1mdurations[i][l]表示第 i 路各班车运行一个循环所用的时间( i=1, 2, …,n )。若设本案例中乘客的到达时间为 arrival ,则$Ri=arrival \mod Ti $表示乘客来到车站时,第 i 路车运行完若干个循环周期后处于最新运行周期内的时间。例如,输入样例中的案例 1 中 1 路车 3 班车的一个运行周期 T1 为 100+200+300=600,乘客到达时间 a r r i v a l = 1000 , R 1 = a r r i v a l m o d T 1 = 1000 m o d 600 ≡ 400 arrival=1000, R1=arrival \mod T1=1000 \mod 600≡400 arrival=1000,R1=arrivalmodT1=1000mod600≡400。这意味着 1路车的 3 班车已经运行了一个循环后 400 时乘客到达车站。于是,乘客需要等待的应该是当前周期内从开始到最近发车时间超过 400 的那班车。等待的时间自然就是从第一个使得差 T i = ∑ j = 1 m d u r a t i o n s [ i ] [ l ] − R i ≥ 0 ( 1 ≤ k ≤ m i ) T_i=\sum^m_{j=1}durations[i][l]-R_i\ge 0(1 \le k \le m_i) Ti=∑j=1mdurations[i][l]−Ri≥0(1≤k≤mi)的值。本例中此值为 (100+200+300) −400 = 600 - 400=200。所有 n 路的等待时间中的最小值即为所求。以上算法思想写成伪代码过程如下。 WORLD-WORST-BUS-SCHEDULE(durations, arrival) 设案例中有 n 路公交,其中班次最多的班数为 m。算法的运行时间取决于第 2~9 行的两层嵌套循环重复次数。外层 for 循环重复 n 次,里层的第 4 行实际上也是一个循环(计算累加和),重复次数最多为 m。同样,第 7~ 8 行的 while 循环也至多重复 m 次。这两个内层的循环是并列的,所以运行时间为 O(nm)。 问题描述 冒泡排序是一种简单的排序算法。该算法反复扫描欲排序的列表,比较相邻元素对,若两者顺序不对,就将它们交换。这样对列表的扫描反复进行直至列表中不存在需要交换的元素为止,这意味着列表已经排好序。算法之所以叫此名字,是缘于最小的元素就像“泡泡”一样冒到列表的顶端,这是一种基于比较的排序算法。 冒泡排序是一种非常简单的排序算法,其运行时间为 O(n2)。每趟操作从列表首开始,以此比较相邻项,需要时交换两者。重复进行若干趟这样的操作直至无需再做任何交换操作为止。假定恰好做了 T 趟操作,序列就按升序排列,我们就说 T 为对此序列的冒泡排序趟数。下面是一个例子。序列为“5 1 4 2 8 ”,对其施行的冒泡排序如下所示。 第一趟操作: ( 5 1 4 2 8 ) −> ( 1 5 4 2 8 ),比较头两个元素,并将其交换。 ( 1 4 2 5 8 ) −> ( 1 4 2 5 8 ) 在 T = 2 趟后,序列已经排好序,所以我们说对此序列冒泡排序的趟数为 2。ZX 在算法课中学习冒泡排序,他的老师给他留了一个作业。老师给了 ZX 一个具有 N个两两不等的元素的数组 A,并且已经排成升序。老师告诉 ZX,该数组是经过了 K 趟的冒泡排序得来的。问题是: A 有多少种初始状态,使得对其进行冒泡排序,趟数恰为 K?结果可能是一个很大的数值,你只需输出该数相对于模 20100713 的剩余 输入 输入包含若干个测试案例。 输出 对每个案例,输出序列的初始情形数对模 20100713 的剩余,每个一行。 输入样例 3 3 0 3 1 3 2 输出样例 1 有的计数问题所涉及的事物间存在着某种关系,这样的问题往往可以表示成一个图(Graph):问题中的每个事物视为一个顶点,两个顶点之间如果存在这关系,就在这两个顶点之间做一条称为边的弧。形式化描述为由问题中的各事物构成的集合,记为顶点集V={v1,v2,…,vn},边集 E={(vi, vj)| vi, vj ∈V 且 vi 和 vj 具有关系}。 例如,图 1-3 将五个人 Adward、 John、 Philips、 Robin和 Smith 之间的朋友关系表示成了一个图。其中,Adward 与 Robin 和 Smith 是朋友,John 与 Philips 和Robin 是朋友, Philips 与 John、 Robin 和 Smith 是朋友,Smith 与 Adward、 Philips 和 Robin 是朋友, Robin 与其他所有人都是朋友。 图 G 记为 设 G= 对图中所有顶点的度数有如下所述的结论。 定理 1-1(握手定理) 设 G= 证 G 中每条边(包括环)均有两个端点,所以在计算 G 中各顶点度数之和时,每条边均提供 2 度,当然,m 条边,共提供 2m 度。 握手定理说明,图中各顶点的度数之和必为偶数 问题描述 百度之星总决赛既是一群编程大牛一决高下的赛场,也是圈内众多网友难得的联欢,在为期一周的聚会中,总少不了各种有趣的游戏。 某年的总决赛聚会中,一个有趣的游戏是这样的: 游戏由 Robin 主持,一共有 N 个人参加(包括主持人), Robin让每个人说出自己在现场认识的人数(如果 A 认识 B ,则默认 B也认识 A),在收到所有选手报出的数据后,他来判断是否有人说谎。 。 Robin 说,如果他能判断正确,希望每位选手都能在毕业后来百度工作。 为了帮 Robin 留住这些天才,现在请您帮他出出主意吧。 特别说明: 1.每个人都认识 Robin。 2.认识的人中不包括自己。 输入 输入数据包含多组测试用例,每组测试用例有 2 行,首先一行是一个整数 N (1 N 为 0 的时候结束输入。 输出 请根据每组输入数据,帮助主持人 Robin 进行判断:如果确定有人说谎,请输出“Lieabsolutely”;否则,请输出“Maybe truth”。 每组数据的输出占一行 输入样例 7 输出样例 Lie absolutely 解题思路 (1)数据的输入与输出 根据题面中对输入文件格式的描述,文件中有若干个测试案例,每个案例的数据以表示人数的整数 N 开头,然后有 N-1 个整数表示除主持人以外的每个人所报告的相识人数。对案例判断其中是否有人说谎,根据计算结果输出一行“ Maybe truth ”(无人说谎)或“ Lieabsolutely”(有人说谎)。N=0 是输入结束的标志。 其中,第 9 行调用过程 PARTY-GAME(a)判断 N 个人中是否有人说谎,是解决一个案例的关键。 (2)处理一个案例的算法过程 在一个案例中,把两个人相互认识看成一种关个无向图 G= 算法 1-11 对一个案例而言,假定包括主持人在内,晚会上有 n 个人,则第 3~5 行的 for 循环将重复 n 次。所以算法对一个案例的运行时间是Θ(n)。 置换与轮换 设有 n 个两两不等的元素 a1, a2, …, an 构成的集合 A,考虑 A 到自身的一个 1-1 变换σ:a’ 1=σ(a1), a’2=σ(a2),…,a’n=σ(an)。换句话说,a’1,a’2,…,a’n 是 a1 , a2, …, an 的一个重排。数学中,称这样的对应关系σ为 A 的一个置换。 【例 1】集合 A={2,4,3, 1},σ (2)=1 ,σ(4)=2,σ(3)=3,σ(1)=4 就是 A 上的一个置换。 设σ为 A={a1, a2, …, an}的一个置换: a2= σ(a1), a3=σ(a2),…, an=σ(an−1),则称σ为 A上的一个轮换。 【例 2】例 1 中,由于σ(2)=1,σ(1)=4,σ(4)=2,故σ可视为 A 的子集合 A1={2,1,4}上的一个轮换σ1。 【例 3】单元素集合 A={a}上的恒等变换σ(a)=a 视为轮换。 置换与轮换之间有如下的重要命题 定理 1-2 集合 A={a1, a2, …, an}上的任何一个置换σ,均可唯一5地分解成 A 的若干个两两不相交的子集上的轮换,且这些子集的并即为 A 【例 4】例 1 中 A={2,4,3,1}上的置换σ可以分解成例 2 中 A1 上的σ1:2→1 ,1→4,4→2 和 A2={3}上的恒等变换σ2:3→3,且 A= A1 A2,A1 A2=∅。 问题 1-10 牛妞排队 农夫 John 有 N (1 ≤ N≤ 10 000)头牛妞,晚上她们要排成一排挤奶。每个牛妞拥有唯一的一个值介于 1~100000 的表示其暴脾气程度的指标。由于暴脾气的牛妞更容易损坏 John 的挤奶设备,所以 John 想把牛妞们按暴脾气指数的升序(从小到大)重排牛妞们。在此过程中,两个牛妞(不必相邻)的位置可能被交换,交换两头暴脾气指数为 X、 Y 的牛妞的位置要花费X+Y 个时间单位。 请你帮助 John 计算出重排牛妞所需的最短时间。 输入 输入文件中包含若干个测试案例数据。每个测试案例由两行数据组成: 第 1 行是一个表示牛妞个数的整数 N。 第 2 行含 N 个用空格隔开的整数,表示每个牛妞的暴脾气指数。 N=0 是输入数据结束的标志。对此案例无需做任何处理。 输出 对每一个测试案例输出一行包含一个表示按暴脾气指数升序重排牛妞所需的最少时间的整数。 输入样例 输出样例 7 解题思路 (1)数据的输入与输出 本问题输入文件包含若干个测试案例,每个案例的输入数据有两行:第 1 行含有 1 个表示牛妞个数的整数 N,第 2 行含有 N 个表示诸牛妞脾气指数的整数。 N=0 为输入数据结束标志。可以将案例中牛妞脾气指数组织成一个数组,对此数组计算按脾气指数升序排列重排牛妞的最小代价。将计算所得结果作为 1 行写入输出文件 其中,第 8 行调用过程 COW-SORTING(a)计算将牛妞们按脾气指数升序排序所花的最小代价,是解决一个案例的关键 (2)处理一个案例的算法过程 将算法思想表达为伪代码过程如下。 算法 1-12 计算将牛妞们按脾气指数升序重排的最小代价的算法过程 算法中设置 b 为数组 a 按升序排序的结果(第 2~3 行)。a、b 元素之间的对应关系是根据对应下标确定的,即 a [i] σ b [ i ] (1≤i≤ n)第 5~18 行的 while 循环每次重复构造 A 的一个轮换子集,并计算完成该子集元素交换的最小代价,累加到计数器 count(第 1 行初始化为 0)中。具体地说,第 6 行取 a 中未曾访问过的元素(a 中访问过的元素置为 0)下标为 j,设新的子集上轮换的首元素 ai。第 10~15 行的 while 循环按条件 b[j]≠ai 重复,构造一个轮换子集。一旦该条件为假(b[j]=a i)意味着轮换完成。在构造过程中,第 11 行子集元素个数 k 自增 1,第 12 行将新发现的元素添加到和 sum(第 7 行初始化为该子集的首元素 ai)中,第 13~14 行跟踪该子集的最小元素 ti (第 7 行初始化为∞)。第 15 行找出下一个对应元素下标 j,第 16 行将已经完成访问的 a[j ]置为 0,且将尚未访问过的元素个数 n(第 1 行初始化为 a 的元素个数)自减 1。一旦完成一个轮换子集的构造(第 10~ 16 行的 while 循环结束)第 17~ 18 行根据子集元素个数 k 是否大于 1 ,按此前讨论的公式决定 count 的增加值算法的运行时间取决于第 11~16 行操作被重复的次数。由于每次重复 a 中的一个元素值被值为 0,而外层循环条件为 a 中非 0 元素个数 n>0,所以第 11~16 行的操作一定被重复a 的元素个数次 N (即牛妞的个数)。在 11~16 行的各条操作中,第 15 行调用 FIND 过程在a 中查找值为 b[j]的元素下标,这将花费 O(N)时间,所以整个算法的运行时间是 O(N2)。 问题 2-1 开源项目 问题描述 开放资源研讨会在一所著名高校举行,各开源项目负责人将项目报名签单贴在墙上,项目的名称以大写形式位于签单的顶部,作为项目的标识。要加入一个项目的学生用自己的用户标识在该项目名下签到。用户标识是以小写字母开头后跟小写字母或数字的字符串。 然后组织者将所有的签单从墙上取下来,并将信息录入系统。你的任务是对每张项目签到表上的学生进行汇总。有些学生过于热情,多次将其名字签在项目签单上。这没关系,这样的情况该学生仅算一次就可以了。要求每个学生只能在一个项目报名,任何在多个项目报名的学生都将被取消资格。 学校里最多有 10000 个学生,最多有 100 个项目贴出报名签单。 输入 输入包含若干个测试案例,每个案例以仅含 1 的一行作为结束标志,以仅含 0 的一行为输入结束的标志。每个测试案例含有一个或多个项目签单。一个项目签单行有一行作为项目名称,后跟若干个学生的用户标识,每行一个。输出对于每一个测试案例,输出对每一个项目的汇总。汇总数据为每行一个项目名后跟报名的学生数。这些数据行应按报名学生数的升序进行输出。若有两个或两个以上的项目报名学生数相同,则按项目名的字典顺序排列 输入样例 UBQTS TXT 输出样例 YOUBOOK 2 解题思路 (1)数据的输入与输出 根据输入文件的格式:含有若干个测试案例,以“0”作为输入结束标志。每个案例的输入数据包含若干行描述多个项目的数据。每个项目的第一行是大写的项目名称,后跟若干行该项目下的学生签名。以“1”作为案例数据结束标志。从头开始,依次读取输入文件中的每一行,存入数组 a 中。遇到“1”则结束本案例数据输入,计算案例中每个项目最终合法的学生签名数,并按输出格式要求将计算所得数据写入输出文件。循环往复,直至读到“0” 。 其中,第 9 行调用计算各开源项目下学生人数的过程 OPEN-SOURCE(a),是解决一个案例的关键。 (2)处理一个案例的算法过程 就一个测试案例而言,每一个开源项目除了标识该项目的名称以外,还对应若干个学生签名。如果一个学生在一个项目中有多个签名,只算一次。对每个学生,只能在一个项目中签名,若输入数据中一个学生的签名出现在多个项目中,则在所有含有该学生签名的项目中删除该签名。最后汇总的就是每个项目的学生个数。为解决一个案例,可以设置两个集合:Projects 和 Students。集合 Projects 用来存放各项目的信息,包括项目名称 name 和项目的学生签名数 number。即, Projects 中的每个元素 project是序偶 算法 2-1 汇总各开源项目报名人数的过程 考察算法 2-1,其中有 2 个集合:第 1 行创建的项目组集合 Projects 和学生的签名集合Students。算法中对这些集合有如下操作: 1 将 元 素 插 入 ( 添 加 ) 到 集 合 中 ,第 10 行调 用 过 程 INSERT(Students, 2 从集合中将指定元素删除。第 15 行调用过程 DELETE(Projects, p)将项目 p 从项目集合 Projects 中删除。 3 在集合中查找特定值元素。第 8 行调用过程 FIND(Students, userid)在学生集合 students中查找签名为 userid 的元素,第 14 行中 FIND(Projects, pname[student])在 Projects 中查找项目名为 pname[student]的元素。 4 将集合中元素按顺序排列。第 20 行 SORT(Projects)对 Projects 中的元素按项目的人数降序排列,若两个或两个以上的项目人数相同则按项目名的字典顺序排列。 通常将集合的1、2、3三种操作 INSERT、DELETE 和 FIND 称为字典操作,实现了字典操作的集合称为一个字典。按此概念,Projects 和 Students 都是字典。第4种 SORT 操作称为排序。排序操作只能对全序集1进行。 若一个案例中有 n 个项目,每个项目的平均报名学生数为 m,则第 7~18 行的操作就要被重复 nm 次。然而,我们并不能就此而断言算法 1 的运行时间为Θ(nm),因为这其中含有对各集合的字典操作。此外,我们还需考虑第 20 行对 Projects 的排序操作所需的时间。 在计算机中,集合有各种表示方式,对应不同的表示方式,上述的 4 种操作方法有所不同,当然也就影响了各操作所需的时间。 集合的线性表表示 把集合中的元素一字排开,每个元素用所在位置(下标)检索——表示成一个线性表,如图 2-1 所示。由于线性表中的元素是用其所在位置检索的,所以可以用来表示可重元素集合(集合中可以存在多个值相同的元素)。在一个线性表 A={a1,a2,…,an}中查找特定值为 x 的元素操作 FIND(A, x),算法从 A 中 a 1 开始逐一地检测每一个元素,直至首次遇到某个 ai=x,或检测完整个线性表没有发现满足条件的元素为止。 图 2-2 展示了对线性表 A={4, 6, 1, 8, 3, 0, 9, 2, 5, 7},查找值 x=3、x=11 和 x=4 的元素时运行 FIND(A, x)的各种情形。图中带箭头的弧线表示依次检测。图(a)是当 x=3 时,查找到特定值元素进行了 5 次检测;图(b)是当 x=11 时查找没有发现特定值元素,检测了 11次,这是最坏情形;图©是当 x=4 时,检测 1 次便找到了特定值元素,这是最好情形。由此可见,在一个具有 n 个元素的线性表中查找特定值为 x 的元素的算法运行时间为 O(n)。 在线性表中进行插入元素操作 INSERT 和删除元素操作 DELETE 的运行时间效率视线性表在内存中的存储方式而有所区别。线性表在内存中常表示为数组(连续存储)或链表(通过指针将相邻元素连接)。 图 2-3(a)展示了要将数据 8 插入到数组的第 3、4 个元素(即值为 1、3 的元素)中间的操作。这需要把第 3 个元素以后(连同第 3 个元素)的所有元素都向后移动一个位置。图2-3(b)展示了要将数组中的第 3 个元素(即值为 1 的元素)从数组中删除的操作。这需要把第 4 个元素以后(连同第 3 个元素)的所有元素向前移动一个位置。由此可见对于数组,无论 INSERT 是还是 DELETE 操作,所需要的运行时间均为 O(n)。 图 2-4(a)展示了将值为 8 的元素插入到链表中两个相邻节点(即值为 1、3 的节点)之间的操作。这只需将值为 1 的节点中指向下一个节点的指针指向新节点,并将新节点中指向下一个节点的指针指向值为 3 的节点就可以了。图 2-4(b)展示了将链表中值为 6、8 的节点之间,值为 1 的节点删除的操作。这只需要将值为 6 的节点的指针域指向值为 8 的节点就可以了。由此可见,对链表的 INSERT 和 DELETE 操作都只需花费常数时间。 对于线性表(无论是数组还是链表)表示的全序集的排序操作,有很多各有特色的算法,如冒泡排序、插入排序、归并排序、快速排序,等等。理论已经证明,只要是基于元素间比较的排序算法,运行时间一定不会小于 n l g n 2 nlgn^2 nlgn2。 全序集的二叉搜索树3表示 全序数据集合还可以表示成二叉搜索树。在这棵二叉树中,左孩子的值不超过父亲的值,而父亲的值小于右孩子的值。由于二叉搜索树中节点是根据元素的值检索的,所以二叉搜索树只能表示无重元素集合(集合中元素值两两不等)。 为了在表示成二叉搜索树 T 的集合中查找等于特定值 x 的节点, 从树根开始将 x 与节点值比较,若相等则查找成功。若 x 小于节点值,则在节点的左子树中继续查找;若 x 大于节点值,则在节点的右子树中继续查找,直至找到或无法继续(当前节点无可继续查找的子树)为止。如图 2-5 所示。查找过程的运行时间最坏情形是在树中无指定值节点,这需要从树根一直查询到一片叶子(没有孩子的节点)。所花费的时间不会超过树 T 的高度。如果含有 n 个节点的二叉搜索树 T 是平衡的(左右孩子的高度一致) ,则其高度为 lgn。所以 FIND(T, x)的运行时间为 O(lgn)。要在二叉搜索树中插入值为 x 的节点,使其保持为一棵二叉搜索树,如同查找方法那样,先找到插入位置,然后将父节点的孩子指针指向新节点就可以了,所需时间也是 O(lgn)。如图 2-6 所示。 类似地,我们可以在 O(lgn)时间内将二叉搜索树中的一个节点删除,使其仍保持为一棵二叉搜索树4。对表示为二叉搜索树的集合,进行一次“中序遍历”,就可以得到该集合的一个排序。所谓中序遍历就是从根开始,先罗列左子树中的每个节点,然后将根列于这些节点尾部,再接着罗列右子树的每个节点。这样每个节点被访问一次,故 SORT(T)耗时Θ(n)。 整数集合的散列表表示 元素值为非负整数或可以转换为非负整数的集合 A,还可以表示成散列表。所谓散列表主体是一个数组 H[0…m−1],其中的每个元素为一个链表。集合 A 中的每个元素 x 通过一个 hash 函数将其值映射为 0~m−1 中的一个整数 i,即hash(x)=i, 0≤i 表 2-1 回到算法 2-1。如果把集合 Students 表示为散列表,则第 8 行中的 FIND(Students, userid)和第10 行的 INSERT(Students, 问题描述 王子 Ray 很想与他美丽的女朋友 Amy 公主结婚。Amy 很爱 Ray,也非常愿意嫁给他。然而,Amy 的父王 StreamSpeed 是一个很坚持的人。他认为他的女婿应当聪敏过人,才能在自己退休后让他女婿来做国王。于是,他要对 Ray 进行一次测验。 国王给了 Ray 一个尺寸为 n×n×n 的魔方,其中包含 n×n×n 个小格子,每个格子可以表示成一个三元组(x, y, z) (1≤x, y, z≤n),每个格子中均有一个数。初始时,所有格子中的数置为零 StreamSpeed 国王会对魔方做下列三种操作 1 对指定的小格加入一数。 输入 输出 对输入文件中的每一个查询,程序应当输出对应的结果——范围(x1, y1, z1)~(x2, y2, z2)中数的总和。所有的结果不超过 1 0 9 10^9 109。 输入样例 10 输出样例 10 解题思路 (1)数据的输入与输出 其中,第 9 行调用计算执行指令序列后魔方状态变化并返回查询指令执行结果的过程PRINCE-RAY-PUZZELE(a),是解决一个案例的关键 (2)处理一个案例的算法过程 这个题目最直观的想法是借鉴解决问题 0-2 的方法,使用一个三维数组 BRICK[1…n, 1…n, 1…n]表示这个大魔方,并将其中每个元素初始化为 0。对每一个 A 操作,做加法: BRICK[x, y, z]← BRICK[x, y, z]+num;对每个 S 操作,做减法:BRICK[x, y, z]← BRICK[x, y, z]+num;对每个 Q 操作,遍历由对角(x 1 , y1, z 1)−(x 2 , y2 , z2)决定的三维区域,累加其中每一个方格 BRICK[x, y, z]的数据并输出: 假定指令数与 n 相当,指令类型均衡(A、S、Q 指令数目相当),则解决该问题的耗时为O(n4 )。为了提高时间效率,我们做如下变通。将魔方中的每个小格视为一个四元组 算法 2-2 解决“王子的难题”问题的算法过程 仍然假定指令数 m 与 n 相当,则第 3~20 行的 for 循环将重复Θ(n)次。每次重复中第 4~14 行的操作,耗时可视为Θ(n)。这是因为第 6 行执行在 BRICK 中的查找操作,按表 2-1,这需要Θ(n)时间。而第 10 或 11 行的在 BRICK 中所做的插入操作,若将元素追加到序列尾部,则耗时为常量。第 17~19 行中对 BRICK 的遍历耗时Θ(n)。总之,算法 2-2 的运行时间为Θ(n2)。解决本问题的算法的 C++实现代码存储于文件夹 laboratory/ Prince Rays Puzzle 中,读者 问题描述 Baidu 年会安排了一场时装秀节目。N 名员工将依次身穿盛装上台表演。表演的顺序是通过一种“画线”抽签的方式决定的 首先,员工们在一张白纸上画下 N 条平行的竖线。在竖线的上方从左到右依次写下 1 至 N 代表员工的编号;在竖线的下方也从左到右写下1 至 N 代表出场表演的次序 接着,员工们随意在两条相邻的竖线间添加垂直于竖线的横线段。 最后,每位员工的出场顺序是按如下规则决定的:每位员工从自己的编号开始用手指沿竖线向下划,每当遇到横线就移动到相邻的竖线上去,直到手指到达竖线下方的出场次序编号。这时,手指指向的编号就是该员工的出场次序。例如在下图所示的例子中,度度熊将第二个出场,第一个出场的是员工 4。 员工在画横线时,会避免在同一位置重复画线,并且避免两条相邻的横线连在一起,即下图所示的情况是不会出现的。 给定一种画线的方案,员工编号为 K 的度度熊想知道自己是不是第一位出场表演的。如果不是,度度熊想知道能不能通过增加一条横线段来使自己变成第一位出场表演。 输入 为了描述方便,我们规定写有员工编号的方向是 Y 轴正方向(即上文中的竖线上方),写有出场次序的方向是 Y 轴的负方向(即上文中的竖线下方)竖线沿 X 轴正方向(即上文中从左到右)依次编号为 1 至 N。于是,每条横线的位置都可以由一个三元组(xl, xr, y)确定,其中 xl, xr 是横线左右两个端点所在竖线的编号,y 是横线的高度。输入的第一行是一个整数 T(T≤50),代表测试数据的组数。每组数据的第一行包含三个整数 N,M,K(1≤N≤100,0≤M≤1000,1≤K≤N),分别代表参与表演的员工人数、画下的横线数目以及度度熊的员工编号。每组数据的第 2~M+1 行每行包含 3 个整数 xl,xr,y(1≤xl ≤N,x r = xl +1,0≤ y ≤1000000),它们描述了一条横线的位置。 输出 对于每组数据输出一行 Yes 或 No,表示度度熊能否通过增加一条横线段来使得自己变成第一位出场表演。如果度度熊已经是第一位出场表演,也输出 Yes。注意,尽管输入数据中员工画的横线高度都是整数,但是度度熊可以在任意实数高度画横线。此外,度度熊和员工一样,在画横线时需要避免在同一位置重复划线,也要避免两条相邻的横线连接在一起。 输入样例 2 输出样例 Yes 解题思路 (1)数据的输入与输出 按输入文件的格式,首先从中读取案例数 T,然后依次读取每个案例的数据。对一个案例,先读取表示员工数、横线数和度度熊编号的整数 N,M,K,然后依次读取每条横线的数据 x l,xr,y,置于数组 a 中。对案例的输入数据 N,M,K 及 a,计算判断度度熊是否能通过添加一条横线而第一个出场,最后将判断结果(Yes/No)作为一行写入输出文件。描述成伪代码如下。 其中,第 10 行调用计算并判断度度熊能否通过添加一条横线第一个出场的过程 TO-BE-FIRST(a, N, K),是解决一个案例的关键。 (2)处理一个案例的算法过程 设所画的最高处的横线高度为 L。则刻画本问题的数据模型是一个二维矩阵 A L + 2 × N : A_{L+2×N}: AL+2×N: A [ 0.. L , 1.. N ] A[0..L,1..N] A[0..L,1..N]。A[0…L, 1…N]。其中每列表示一条竖线,若在两条相邻竖线 j 和 j+1 之间高度为 i 处有一条横线段,则 A[i, j]=right(→),A[i, j+1]=left(←),为了与题中图示方向一致,我们对矩阵的行的编号与自上而下的普通矩阵顺序相反(自下而上)。例如,测试案例 1 数据可表示为图 2-8 所示的 8×4 矩阵。 利用这个矩阵,我们可以找出任何一个员工自上而下划线的路径:从与员工的编号 j 相同的竖线顶端向下——对应矩阵 A 的第 j 列从 A[L+1, j]开始向下搜索,假定在 i处搜索第一个非 down,若 A[i, j]为 right 则下一步搜索应从A[i, j+1]开始往下进行,否则从 A[i, j−1]开始往下搜索。如此循环往复,直至到达某一条竖线的底端之下,此时的列编号就是 j 号员工出场的顺序号。将划线过程中经过的竖线段表示成三元组(yl, yu , x) ,其中 yl 表示竖直线段的下端位置,yu 表示该线段的上端位置,即(yl, yu)表示线段高图 2-8 表示测试案例 1 的符号矩阵度区间,x 表示该竖线段所在竖线的编号,则 j 号员工的划线路径就可表示成这些三元组的集合 path j 。特殊地,可以找到度度熊的划线路径 pathK。其中,底部的第一行全为 down,表示虚拟的出口;顶部第八行全为 down,表示虚拟的入口。 其中,底部的第一行全为 down,表示虚拟的出口;顶部第八行全为 down,表示虚拟的入口。 例如,在上述的案例 1 中,考虑 3 号的度度熊。从 A[7, 3]起,竖直搜索到 A[5, 3]= ←,故切换到 A[5, 2]。,切换到 A[4, 1]。从 A[4, 1]起,竖直搜索到 A[1, 1] =→,故切换到 A[1, 2]。从 A[1, 2]竖直搜索到出口 A[0, 2]。这样,度度熊的路径可表示成 path3={(0, 1, 2),(1, 4, 1),(4, 5, 2),(5, 7, 3) } 相反方向的搜索过程,可以确定每一个出场顺序对应的员工的划线路径。特殊地,可以找到第一个出场的员工的划线路径 backpath1。例如,在案例 1 中,从 A[0, 1]开始竖直向上搜索到 A[1, 1]= →,故切换到 A[1, 2],继续竖直向上搜索到 A[2, 2]= →,切换到 A[2, 3]。从A[2, 3]竖直搜索到 A[4, 3]= →,切换到 A[4, 4]。从 A[4, 4] 继续竖直向上搜索,直至入口 A[7, 4]均为 0。这样,第一个出场员工的划线路径为 backpath 1={(0, 1, 1), (1, 2, 2), (2, 4, 3), (4, 7, 4)}。将度度熊的划线路径与 1 号出场员工的划线路径进行比较, 若两者各有一条竖线相邻且高度有相交,则在相交部分任一点处划横线,度度熊就能第一个出场。否则,不行。例如,上例中度度熊划线路径中的(5, 7, 3)和 1 号出场员工划线路径中的(4, 7, 4)相邻,且(5, 7) ∩ (4, 7)=(5, 7)。故度度熊可以通过从第 3 条竖线到第 4 条竖线之间再画一条横线(高度介于 5~7) ,使自己第一个出场。当然,度度熊也可以在出口前(第 2 条直线底端(0.1)向左划一条横线,到第一个出口出场。 )用矩阵表示划线模型,实现起来会遇到两个问题:其一,由于设计时并不确切知道最高横线高度为几何,为适应所有可能的案例数据,矩阵的行数必须定义成题面中说明的最大值1000000。其二,当员工数 N 达到最大值 100 时,矩阵的规模达到 1000×1000000,这个开销是很大的。并且,在搜索划线路径时,算法的运行时间也很奢侈。为提高算法的时空效率,我们将矩阵中表示第 i 条竖线的第 i 列,表示成一个集合 linei,其中的元素为二元组 (看不懂) 问题描述 德州小镇达布威利受到外星人的攻击。外星人挟持了小镇的一些居民,押解到他们绕地球环行的飞船里。过了一段难熬的时间,外星人克隆了一批被俘者,并将这些人连同他们的多个复制品放回了小镇达布威利。于是,小镇里可能有 6 个相同的名叫Hugh F. Bumblebee 的人:Hugh F. Bumblebee 本人及其 5 个复制品。联邦调查局责成你查清小镇里的每个人有多少个复制品。为了帮助你完成任务,调查局已经收集了每个人的 DNA 样本,同一个人的所有复制品具有相同的 DNA 序列,而不同的人的 DNA 序列一定是不同的(已知小镇里从来没有过双胞胎)。 输入 输入文件包含若干个测试案例。每个案例的首行数据包含两个整数 1≤n≤20000 和 1≤m≤20,分别表示小镇人数和每个 DNA 序列的长度。接下来的 n 行表示这 n 个人的 DNA 序列:每行含有由字符’A’, ‘C’, 'G’或’T’构成的长度为 m 的字符串。数据中 n=m=0 的案例是输入数据的结束标志。 输出 对每个案例,程序输出 n 行,每行含有 1 个整数。第一行表示没有复制品的人数,第二行表示有一个复制品的人数。第三行表示有两个复制品的人数,依此类推:第 i 行表示有 i-1个复制品的人数。例如, 一共 11 份样本,其中 1 份来自 John Smith,其余 10 份来自 Joe Foobar,则输出的第 1 行和第 10 行为 1,其余所有各行均为 0。 输入样例 9 6 输出样例 1 解题思路 (1)数据的输入与输出 按本题输入文件格式的描述,每个测试案例的第一行含两个分别表示 DNA 串个数和每个 DNA 串长度的整数 n 和 m。后面跟 n 行,每行一个 DNA 串。n=0 且 m=0 为输入结束标志。依次读取案例中的 DNA 串。由于 DNA 串有重复情形,所以将这些串组成的集合 a表示成数组是合适的。对 a 处理计算出每一个 DNA 样本的克隆数,同样由于不同克隆数的DNA 样本数有可能相同,所以将这些数据组织成数组 solution 也是合适的。将 solution 的每一项数据作为一行写入输出文件。表示成伪代码过程如下。 其中,第 8 行调用计算不同克隆数的 DNA 串数目的过程 FIND-THE-CLONES(a),是解决一个案例的关键。 (2)处理一个案例的算法过程 解决一个给定了输入 a 的测试案例要用到两个集合:其一是由 n 个 DNA 串构成的样本集合 DNAS,其中的元素可视为表示 DNA 串的 dna 及表示这个串的复制份数的 copies 构成的序偶 算法 2-7 解决“寻找克隆人”问题一个案例的算法过程 由于对集合 DNAS 的操作仅限于查找和插入,故将其表示为散列表是合适的,而 solution中元素的第一个属性 copies 也是该元素的输出顺序,因此这个属性的值可以作为该元素存储在数组中的下标。换句话说,将 solution 表示成元素类型为整数(solution[i]表示有 i 个副本的 DNA串的个数)的数组是合适的,在算法 2-2 中也是这样体现的。如此,该算法的运行时间为Θ(n),这是因为第 2~7 行的 for 循环重复 n 次,每次重复对 Hash 表 DNAS 的查找与插入操作耗时为常数,第 9~10 行的 for 循环至多重复 n 次,循环体中的算术运算和赋值运算耗时亦为常数。解决本问题的算法的 C++实现代码存储于文件夹 laboratory/Find the Clones 中,读者可打开文件 Find the Clones.cpp 研读,并试运行之。C++代码的解析请阅读第 9 章 9.4.1 节中程序9-43 的说明。 问题 2-5 疯狂搜索 问题描述 很多人热衷于猜谜,并不时地为谜题而抓狂。有一个这样的谜题要在一段给定的文本中找出与之相关的一个素数。这个素数可能是文本中指定长度的不同子串个数。要解决这个难题看来需要求助于一台计算机和一个好的算法。你的任务是对给定文本和构成文本的字符数 NC,写一段程序确定文本中长度为 N 的不同的子串个数。例如,对文本“daababac”已知 NC=4,文本中长度 N=3 的不同子串分别为: “daa” “aab”“aba”“bab”“bac”。所以,答案为 5。 输入 输入包含若干个测试案例,每个案例包含两行数据:第一行含有两个用一个空格隔开的整数,N 和 NC。第 2 行是一段作为搜索对象的文本。假定这段由 NC 字符组成的文本中,长度为 N 的子串个数不超过 16000000。N=0,NC=0 为输入数据结束的标志。 输出 输入样例 3 4 输出样例 5 解题思路 (1)数据的输入与输出 按题面对输入文件格式的描述,依次对每个测试案例先从输入文件中读取 N 和 NC,然后读取文本行 text。计算 text 中长度为 N 的不同子串个数,将计算结果作为一行写入输出文件。直至从输入文件中读到 N=0 且 NC=0。表示成为代码过程如下 其中,第 6 行调用计算文本行中所含给定长度的不同子串个数的过程,是解决一个测试案例的关键。 CRAZY-SEARCH (text, N) (2)处理一个案例的算法过程 本题的实质是要计算出文本 text[1…length]中所有长度为 N 的子串构成的集合统计出该集合的元素个数(相同的子串仅计数 1 次)。动态维护 text 的子串集合 S(初始化为∅),对每一个长度为 N 的子串 s=texti…i+N,检测是否 s∈S 中出现过。若则将 s 加入 S。具体过程可表示为如下的伪代码。 算法 2-8 解决“疯狂搜索”问题一个案例的算法过程 这里,对集合 S 只有查找“FIND(S, s)”和加入“INSERT(S, s)”两种操作。因此,S 可以是任何一种字典。对字典操作而言,根据表 2-1 知,散列表是最省时的。但是,存入散列表中的元素必须是非负整数。本题中,如果将动态集合 S 表示为散列表,则需要将加入其中的字符串转换为非负整数。输入中的 NC 表示构成文本 text 的字符个数,例如输入样例中text=“daababac”,它是由 a,b,c,d 这 4 个字母构成的。若将 a 对应 0,b 对应 1,c 对应 2,d对应 3,则 text 的任何一个子串,可以唯一地对应一个 4 进制整数。例如,子串 daa 对应 3 × 4 2 + 0 × 4 + 0 = 48 3×4^2+0×4+0=48 3×42+0×4+0=48,而 aab 则对应 3 × 4 2 + 0 × 4 + 1 = 1 3×4^2+0×4+1=1 3×42+0×4+1=1,… 如此,过程的运行时间为Θ(length),即 text 的长度 在信息处理中,时常出现在一个文本串中查找一个模式的发生位置的问题。例如,文本是正在编辑的一个文档,要查找的模式是用户提供的一个具体单词。如图 2-9 所示,要在文本串 T =“ABCABAABCABAC”中查找模式 P =“ABAA”的首次发生。该模式在文本中仅出现了一次,偏移量为 s = 3。模式中的每一个字符通过一根竖线与文本中匹配的字符连接, 所有匹配的字符显示有阴影。这一问题称为串匹配问题。设所有合法字符构成的集合 Σ 是一个有限集,称为字母表。Σ表示用字母表 Σ 中的字符构成的所有有限长度的串的集合。零长度空串,用 ε 表示,也属于 Σ。我们将文本搜索中的文本和模式均视为 Σ*中的字符串 对文本 T [1…n]和模式 P[1…m]解决串匹配问题最直观的算法是利用一个循环对 n−m + 1 个可能的 s 值的每一个,检测条件 P[1…m] = T [s + 1…s + m]是否成立,来查找首个有效偏移量,如图 2-10 所示。 图 2-10(a)中,偏移量 s=0,P[1]与 T[1]匹配(用竖线相连),但是 P[2]≠T[2]遇到一个失配(用一个叉表示),s 自增 1 进入图 2-10(b) 。在图 2-10(b)中 s=1,P[1]≠T[2]又遇到一个失配, s 自增 1,进入图 2-10 ©。在图 2-10 ©中 s=2, P[1]=T[3], P[2]=T[4], P[3]=T[5],得到一个完整的匹配。 将此想法描述成伪代码过程如下 算法 2-9 计算文本为 T[1…n],模式为 P[1…m]的串匹配的强力算法 STRING-MATCHER 过程的运行时间主要在于第 5 行的比较运算 T[s+i]=P[i]的执行次数,最坏情形是每次失配都发生在 P[m]与 T[s+m]处,即 s 从 0 到 n−m 的 n−m+1 个取值匹配都需做 m 次比较。因此运行时间是 O((n−m + 1)m)(见图 2-11)。图 2-11 展示了强力匹配算法对 n=9,m=4 的一个最坏情形 T=“AAAAAAAAAB”,P=“AAB”的执行过程:图(a)~图(f)中对 s 的每一种合法取值(共有 6=n−m+1 个值:0,1,2,3,4,5),模式的每个元素(共有 4 个带有阴影的元素)都要与对应的文本元素(带有阴影的元素)进行比较,比较次数为 6×4=24。 事实上,就上例而言,不是每次匹配都要比较 4 对元素。因为除了第一次匹配时比较了4 对元素外,每得到一个失配(第一次出现在 s=0,i=4 处,最后一次出现在 s=4,i=4 处),我们观察到,模式中的 P[1…3]是与文本中的 T[s+1…s+3]匹配的,并且 P[1…3]的前缀 P[1…2]恰为 T[s+1…s+3]的后缀。这样,当我们将偏移量 s 自增 1 后,就知道 T[s+1…s+2]与 P[1…2]是匹配的,所以比较可以从 i=3 开始进行。这样,就只需比较两对元素(P[3]、T[s+3]和 P[4]、T[s+4]),从而大大减小了比较的次数(见图 2-12)。 利用模式 P 的结构特点加速串匹配的过程,最著名的当属 KMP 算法5(该算法是由Knuth、Pratt 和 Morris 各自独立发明的),它的运行时间可从算法 2-9 的Θ(n−m+1)减少到线性的Θ (n+m)。 问题描述 Pandora 星球上的人们也和我们一样要编写计算机程序。他们向地球偷学的程序由大写字母(‘A’到‘Z’)组成。在 Pandora星球上,黑客们也制造了一些计算机病毒,所以 Pandora 星球人也向地球人偷学了病毒扫描算法。每一种病毒都有一个由大写字母组成的模式串,若一个病毒的模式串是某个程序的一个子串,或模式串是程序逆向串的一个子串,他们就认为该程序被病毒感染了。给定一个程序以及一系列病毒模式串,请编写一个程序确定给定的程序感染了多少个病毒。 输入 对每个测试案例,输入含有若干个测试案例。输入的首行是一个表示测试案例数的整数T(T≤10)。 第二行是一个表示病毒模式串数目的整数 n(0 < n≤250)。后跟 n 行,每一行表示一个病毒模式串。每一个模式串表示一种病毒,这 n 个串两两不同,因此表示有 n 种不同的病毒。每个模式串至少包含一个字符,且长度不超过 1000。测试案例的最后一行是表示一个程序的串。程序可能表示为压缩格式,压缩格式由大写字母和“压缩符”组成。压缩符的形式为[qx]其中,q 是一个整数(0 < q ≤ 5 000 000);而 x 是一个大写字母。它的意义是在原程序中有 q 个连续的字母 x。例如,[6K]意为原程序中此处为“KKKKKK”。于是,若压缩程序形为 AB[2D]E[7K]G 3 输出样例 0 解题思路 (1)数据的输入与输出 按输入的文件格式,首先从中读取案例数 T,然后依次读取各个测试案例。对每个案例,先从输入文件中读取病毒种数 n,然后读取 n 个表示病毒的文本行,组成数组 virus。最后读取表示程序的文本串 program。对案例数据 virus 和 program,计算 program 中所含病毒数,将计算结果作为一行写入输出文件。 其中,第 10 行调用 COMPUTER- VIRUS-ON-PLANET-PANDORA(virus, program) 计算文本行中所含给定长度的不同子串个数的过程,是解决一个测试案例的关键。 (2)处理一个案例的算法过程 对于一个案例数据 virus 和 program,设置一个计数器 count(初始化为 0) ,依次检测中的每一个病毒模式 virus[i]及其逆向串是否为 program(必要时需解压缩)的子串(即 virus[i]及其逆向串是否与 program 串匹配) 。若是,则 count 自增 1。检测完整个数组 virus,count 即为所求。 算法 2-10 解决“Pandora 星球上的计算机病毒”问题一个案例的过程 算法中第 3 行调用的 EXTRACT 过程,完成对程序串的解压缩操作。具体操作如下。 算法 2-11 对程序串解压缩的算法过程 我们在前面的表 2-1 中罗列出了集合的各种表示对字典操作的效率的影响,在其中我们还给出了全序集在这些表示方式下的一个重要操作——排序的可行与否。这是因为对于全序集而言,所有元素按一定顺序(升序或降序)罗列出来,本身就为集合增添了更多有用的信息。例如,对一个升序排列的序列 a1,a2,…,an,我们可以用“二分查找”法快速地在其中查询特定值 x 元素的存储位置:设 q=(1+n)/2,若 aq =x 则找到这样的元素位置 q。若否,则或 x < a q x 假设对 A[1…n]的归并排序的运行时间为 T(n),则对 A[p…q]和 A[q+1…r]的归并排序各自都耗时 T(n/2),加上调MERGE(A, 1, q, n)的耗时Θ(n),我们得到 Θ ( n l g n ) Θ(nlgn) Θ(nlgn) 冒泡排序的运行时间是 Θ (n2) 问题描述 对一个序列度量其“杂乱”程度的方法之一是,计数序列中不符合从小到大的顺序的元素对数。例如,按此方法,字母序列“DAABEC”的度量为 5。因为 D 比排在其右边的 4 个字母大,而 E 排列在其右边的 1 个字母大。这种度量方法称为序列的逆序数。序列“AACEDGG”仅有一个逆序(E 和 D)——它几乎是排好序的。而序列“ZWQM”有 6 个逆序(这是一个最“杂乱”的序列——反向的序列)。 请你对一个由 DNA 串(串中仅含四个字母 A,C,G 和 T)组成的序列进行排序。排序规则并非字典顺序,而是按它们的逆序数从小到大的顺序。 输入 输入文件的第一行含两个整数 n(0 输出 将输入文件中的 m 个串按逆序数从小到大的顺序,每个一行输出到输出文件。 输入样例 10 6 输出样例 CCCGGGGGGA (1)数据的输入与输出 根据输入文件格式,先从输入文件中读取表示串长和串数的 n 和 m。而后读取 m 行,每行一个串,组织成数组 DNAS[1…m]。对 DNAS 按各个串的逆序数升序排序。把排好序的DNAS 每行一个串写入输出文件中。 其中,第 7 行调用的计算 DNAS 中每个串的逆序数,并按逆序数的升序对 DNAS 排序的过程 DNA-SORTING(DNAS),是解决本问题的关键。 (2)处理一个案例的算法过程 首先,我们需要有一个对由 4 个符号(A,C,G,T)组成的 DNA 串 dna 计算逆序数的算法。设置一个计数器 count(初始化为 0),按逆序的意义,对串进行扫描,第 i 个元素dna[i]计算排在其之前大于它的元素个数,将其累加到 count 中。扫描完毕后所得 count 即为所求。为了计算 dna[i]之前大于它的元素个数,我们对符号 C、G、T 各设置一个计数器 C C 、 C G 、 C T C_C、C_G、C_T CC、CG、CT(均初始化为 0),它们各自跟踪第 i 个元素之前 C、G、T 的个数。对于 dna[i],若为 这个算法的运行时间取决于第 3~13 行的 for 循环的重复次数 n。每次重复,循环体内的操作耗时为Θ(1)。于是算法的运行时间为Θ(n)。 利用 INVERSION 过程,我们来解决 DNA 排序问题。创建临时序列 a,将 DNAS[1…m]中每个串连同其逆序数 inv 构成的二元组(dna, inv)加入 a。然后对 a 按元素的 inv 属性的升序排序,将排好序的 a 中元素的 dna 属性依次复制回 DNAS。将其具体过程写成伪代码如下。 cpp 问题描述 度度熊拥有一个自己的 Baidu 空间。度度熊时不时会给空间朋友赠送礼物,以增加度度熊与朋友之间的友谊值。度度熊在偶然的机会下得到了两种超级礼物,于是决定给每位朋友赠送一件超级礼物。不同类型的朋友在收到不同的礼物时所能达到的开心值是不一样的。开心值衡量标准是这样的:每种超级礼物都拥有两个属性(A, B),每个朋友也有两种属性(X, Y),如果该朋友收到这个超级礼物,则这个朋友得到的开心值为 AX+BY。由于拥有超级礼物的个数有限,度度熊很好奇:如何分配这些礼物,才能使好友的开心值总和最大呢? 输入 第一行 n 表示度度熊的好友个数。 输出一行一个值表示好友开心值总和的最大值。 输入样例 4 输出样例 118 解题思路 (1)数据的输入与输出 根据输入文件格式的描述,首先需要从输入文件中读取朋友个数 n,然后读取 n 个朋友的属性数据,组织成两个数组 X[1…n]及 Y[1…n]。最后从输入文件中读取两种礼物的属性及个数:A1,B1,k1 和 A2,B2,k2。对输入数据计算给各位朋友的礼物分配,以及朋友们的最大开心值总数。将所得结果作为一行写入输出文件。 其中,第 9 行调用计算朋友们最大开心值的过程 GIFTS(X, Y, A1, B1, k1 , A2, B2, k2),是解决问题的关键。 由于第 i 个朋友对两种礼物的开心程度都可以算出来,分别为 A iX1+BiY1、 AiX2+BiY (i=1,2, …, n)。可以根据这两个值的大小,决定送给第 i 个朋友的礼物种类。可以维护两个集合 S1,S2,前者存放送给第 1 种礼物的朋友编号及该朋友得到礼物的开心值,后者存放送给第 2 种礼物的朋友的同样信息。如果 S1 的元素个数 n1 超过 k1,则将 n1−k1 个开心值最小的朋友的编号连同他们接受第 2 种礼物的开心值转移到 S2 中。若 S2 的元素个数 n2 超过 k2,对 S2 做同样的操作。最后,将 S1 中各元素的开心值之和与 S2 中各元素开心值之和相加即为所求。 算法 2-14 解决“度度熊的礼物”问题的过程 若将和表示成线性表(数组),且将新加入的元素置于尾部,则第 3~6 行的 for 循环耗时Θ(n)。第 8~13 行中对线性表进行排序的过程 SORT 的调用至多被执行一次,理论上耗时Θ(nlgn)。第 14 行需要计算 S1 和 S2 中元素值得和,耗时Θ(n)。因此,算法至多耗时Θ(nlgn)。 问题描述 我们刚接到 Pizoor 通信公司的关于一个特殊系统的订单。该系统由若干设备组成。每一种设备我们可以从若干个厂商中挑选。同一种设备,不同厂商的最大带宽与价格有所不同。将系统所有设备带宽的最小者称为全局带宽(B),所选构成通信系统的各个设备的价格之和称为总价格§。我们的目标是对每一种设备选择一个厂商,使得 B/P 最大。 输入 输入文件的第一行包含一个整数 T (1≤T≤10),表示案例数。接着输入各个案例的数据。每个案例的第一行包含一个整数 n (1≤n≤100),表示通信系统中的设备数,后跟表示各个设备的 n 行数据,每行以表示生产厂家数的 mi 开头,后跟 mi 对表示每个厂商所供设备带宽与价格的正整数。 输出 你的程序对每个输入案例产生并输出一行仅含一个表示最大可能 B/P 的数据,该数据舍入为小数点后 3 位。 输入样例 1 输出样例 0.649 解题思路 (1)数据的输入与输出 按输入文件格式,先从其中读取案例数 t,然后依次读取每个案例的数据。案例的第一行仅含表示设备种数的 n,其后的 n 行每行开头的整数 m 表示一种设备的提供商个数,然后是 mi 对表示一个商家提供的设备的带宽 b 和价格 p。将 n 种设备的供货数据组织成嵌套数组:devices[1…n],其中的 devices[i]是一个具有 mi 个元素的数组 d e v i c e s [ i ] [ 1.. m i ] devices[i][1..m_i] devices[i][1..mi]其每个元素 d e v i c e s [ i ] [ j ] devices[i][j] devices[i][j]为表示第 i 种设备的第 j 个供货商给出的带宽、价钱的二元组(b, p)。将所有品比 B/P,将计算所得精度为 3 位小数的结果作为一行写入输出文件。 其中,第 14 行调用计算配置所有设备的最大性价比的过程 COMMUNICATION-SYSTEM(devices, bands),是解决一个测试案例的关键。 (2)处理一个案例的算法过程 对一个案例的数据 devices 和 bands,由于目标是计算最大的 B/P,其中 B 是所选设备中的最小带宽,P 是所选取的价格之和。为此,我们考察 bands 中的每一个值 B,它能充当最优解中 B 的角色必须满足对每一种设备,至少存在一个供应商,其提供的设备带宽 b≥B。对特定的 B,还需考虑使得所选设备的总价 P 较小。这可以通过在每种设备中选取在 B 满足要求的前提下(b≥B),最小的价格 p 来达到。为快速地在 devices[i]中选取合适的设备约束(b, p),我们可以事先将 devices[i]按 b 属性的降序排序,从头开始依次检测(b, p) ∈devices[i]的 b 是否不小于 B,在满足此条件的设备中选取较小的 pmin 并累加到 P。。一旦检测到 b>B 则可立即停止在 devices[i]的搜索(如果 devices[i]未排序,则需对其进行全盘搜索)。若 devices[i]中没有带宽 b 不小于 B 的设备,则放弃此 B,检测 bands 中下一个元素。以此提高扫描效率对 bands 的元素 B 跟踪按上述方法确定的 P,跟踪最大的 B/P 即为所求。上述算法思想写成伪代码过程如下。 算法 2-15 解决“通信系统”问题一个案例的算法过程 算法中,第 2~3 行对每个 devices[i] (1≤i≤n)按元素的 b 属性的降序排序,耗时Ω(n2lgn)。假设 m=max{m1, m2, …, mn},第 4~19 行的三重嵌套循环中,第一层重复 O(nm),第二层重复 n 次,第三层重复 O(m)。于是算法的运行时间为 O(n2m2)。 在很多应用问题中,还会涉及同质集合(集合中元素类型相同)间的并、交、差运算。实现这些运算通常需要对集合的元素进行扫描。 算法 2-16 显然,每个操作过程都要对集合做扫描、查询、插入操作。集合在计算机中的不同表示,也会影响集合的这些操作的运行效率。如果将集合表示为线性表,并假设 A 与 B 的元素个数相当(设为 n),则实现这三个算法的运行时间均为Θ(n 2)。 问题描述 众所周知,计算机调度是计算机科学的一个经典问题,对这个问题的研究由来已久。机器调度问题与通常在满足约束条件下的调度问题不尽相同,此处我们考虑 2 机调度问题 设有两台计算机 A 与 B。 A 机有 n 种工作模式,分别记为 mode_0, mode_1, …, mode_n−1。相仿地,B 机有 m 种工作模式,记为 mode_0,mode_1,…,mode_m−1。它们总是从 mode_0开始工作。有 k 个任务,对每个任务而言均可在两台机器的特定模式下处理。例如,job 0 可以在 A机的 mode_3 或 B 机的 mode_4 下处理,job 1 可以在 A 机的 mode_2 或 B 机的 mode_4 下处理,等等。于是,job i 连同其所受约束可表示为三元组(i, x, y),意为其可在 A 机的 mode_x或 B 机的 mode_y 下处理。显然,要完成所有任务的处理,需要时时变换计算机的工作模式。不幸的是,计算机从一种工作模式变换到另一种工作模式必须先关机,然后再启动才能切换。写一个程序,通过变换任务的处理顺序,并指定任务合适的机器,使得重启计算机的次数最小。 输入 输入文件包含若干个测试案例。每个案例的第一行包含三个整数:n,m (n,m < 100)及 k (k < 1000)。接着 k 行给出 k 个任务的约束条件,每行表示成一个三元组:i,x,y。输入文件以一行仅含 0 的数据作为结束标志。 输出 每个案例输出一行包含表示最小重启机器次数的整数。 输入样例 5 5 10 输出样例 3 解题思路 (1)数据的输入与输出 根据输入文件的格式描述,每个案例的第一个数据是表示 A 机模式数的 n,n=0 是输入文件结束标志。对每个 n>0 的案例,接下来需要读取表示 B 机模式数和任务数的 m 和 k。接下来是描述各任务约束的 k 组数据(i,x,y)。把这 k 组数据组织成三个数组 i[1…k],x[1…k]和 y[1…k]。对案例数据 n,m,i,x,y 计算完成所有任务的最小开机次数,将计算所得结果作为一行写入输出文件。直至从输入文件中读出的 n 为 0。 其中,第 9 行调用计算完成所有任务所需最小开机次数的过程 MACHINE-SCHEDULE(n, (2)处理一个案例的算法过程将 n+m 个模式表示为 n+m 个集合,为方便计组织成数组 mode[0…n+m−1]:A 机模式 mode_0,mode_1, …, mode_n−1 为 mode[0…n−1], B 机模式 mode_0, mode_1, …, mode_m−1 为 mode[n…n+m−1]。将输入中每个任务的约束数据(i, x, y)按其能运行的模式分别加入到集合 mode[x]、mode[n+y]中。例如输入样例可表示为:mode[0]={0,1,2,3},mode[1]={4,5,6,7},mode[2]={8},mode[3]={9},mode[4]=∅,mode[5]={0,4},mode[6]={1,5},mode[7]={2,6,8,9},mode[8]={3,7},mode[9]= ∅。为解决此问题,我们采取如下的“贪婪”策略:每次都选取可运行最多任务的模式开机。这样就可以在最少次启动机器后就能完成所有任务的运行。例如,在输入样例中,所有的任务为{0,1,…,9}。先选取欲运行的任务集合为 mode[0]={0,1,2,3},其基数为 4(最大之一),且符合 A 首次开机所处模式。记录开机次数为 1。在所有模式中去除{0,1,2,3}(意味着运行这些任务)后,各模式状态为:mode[0]= ∅, mode[1]={4, 5, 6, 7}, mode[2]={8}, mode[3]={9}, mode[4]=∅, mode[5]={4},mode[6]={5},mode[7]={6,8,9},mode[8]={7},mode[9]= ∅。当前尚未运行的任务变成了{4, 5, 6, 7, 8, 9}。接着选取欲运行的任务集合为 mode[1]={4,5,6,7},基数为 4(最大者),开机次数增加 1 为 2。运行任务{4,5,6,7},则所有模式的状态为:mode[0]=∅, mode[1]=∅, mode[2]={8}, mode[3]={9}, mode[4]=∅, mode[5]=∅, mode[6]=∅,mode[7]={8,9},mode[8]=∅,mode[9]= ∅。尚存任务为{8,9}。选取基数最大的模式 mode[7]={8,9}为欲运行任务,运行之,开机次数增加为 3。在各模式中去除{8,9}后完成所有任务的运行。开机次数 3 即为所求。一般地,设置当前尚未运行的任务集合 jobs,初始化为全体任务{0,1,…,n+m−1}。设置当前准备运行的任务集合为 R,由于两台机器首次开机总是处于 mode[0]及 mode[n],所以 R 初始化为 mode[0]及 mode[n]中基数较大者。设置一个计数器 num 用来跟踪开机次数,初始化为 0。每次从所有模式中去除 R 中的任务,同时从 jobs 中去除 R(意味着这些任务已经完成运行) ,num 增加 1(意味着增加一次开机) 。将 R 置为当前各模式中基数最大者,准备下一次开机。循环往复,直至 jobs 为空。写成伪代码过程如下。 问题描述 你供职于由一群丑星作为台柱的信天翁马戏团。你刚完成了一个程序编写,它按明星们姓名字符串的长度非降序(即当前姓名的长度至少与前一个姓名长度一样)顺序输出他们的名单。然而,你的老板不喜欢这种输出格式,提议输出的首、尾名字长度较短,而中间部分长度稍长,显得有对称性。老板说的具体办法是对已按长度排好序的名单逐对处理,将前者放于当前序列的首部,后者放在尾部。如输入样例中的第一个案例,Bo 和 Pat 是首对名字,Jean 和 Kevin 是第二对,余此类推。 输入 输入包含若干个测试案例。每个案例的第一行含一个整数 n(n≥1),表示名字串个数。接下来 n 行每行为一个名字串,这些串是按长度排列的。名字串中不包含空格,每个串至少包含一个字符。n=0 为输入结束的标志。 输出 7 解题思路 (1)数据的输入与输出 按输入文件格式,读取每个测试案例第一行中的整数 n,然后读取案例中已经按长度排好序的 n 个丑角的名单,组织成一个序列 names。将 names 中的名字串按老板的意见重排,然后逐一写入输出文件。案例数据 n=0 为输入文件结束标志。 其中,第 10 行调用按老板意见重排名单 names 的过程 SYMMETRIC-ORDER(names)是解决一个案例的关键。 (2)处理一个案例的算法过程 对于存储于序列中按长度升序排列的名单 names,要按老板的意见重排,我们需要为names 设置两个位置指针 i 和 j,分别初始化为 2 和 n+1。将 names[i]移到 names[j]之前,且 i自增 1,j 自减 1。重复此操作,直至 i>⎣n/2⎦1(n 为偶数)或 i>⎣n/2⎦+1(n 为奇数)。例如,对输入样例中的案例 1 的数据,重排过程如图 3-1 所示。 输入样例中的案例 1 中,名单中共有 n=7 个名字。图 3-1(a)表示的初始状态,i 为 2,j 为 8(=n+1)。将 Pat(=names[i])移到 Marybeth 之后(names[j]之前),如图 3-1(a)中的箭头弧所示,且 i 自增 1 为 3,j 自减 1 为 7 得到图 3-1(b)所示的状态。对(b)状态重复将 names[i]移到 names[j]之前,且 i 自增 1、 j 自减 1 的操作,得到状态 © 。此时, i=4=3+1=⎣n/2⎦+1达到临界点。做最后一次将 names[i]插入到 names[j]之前,且 i 自增 1、j 自减 1 的操作,达到最终状态(d)。将这样的模拟重排过程表示为处理一般情况下名单的伪代码如下。 算法 3-1 解决“对称排序”问题一个案例的算法过程 算法的运行时间取决于第 6~10 行的 while 循环重复次数显然该循环重复 m=Θ(n/2)=Θ(n)次。每次重复除了第 7、10 行的常数时间操作外,第 8 行要在序列 names 中插入元素,而第 9 行要在其中删除元素。如果把 names 表示成数组,对照表 2-1 知,这两个操作都将耗时Θ(n)。这样,算法 3-1 的运行时间为Θ(n2)。如果将 names 表示为链表,对照表 2-1 知,在其中插入和删除元素耗时均为Θ(1)。这样算法 3-1 的运行时间为Θ(n) 问题 3-2 边界 问题描述 需要编写一个程序,用来为如同图 3-1 中表示的位图中的一个封闭路径描绘出其边界。封闭路径沿栅格线逆时针行进,即总是行进于栅格之间(图中粗线条)。于是,循着路径,像素上的边界就位于路径的“右”边。位图的规模是 32×32,并以左下角的坐标定为(0,0)。位图中的封闭路径一定不会经过位图的边缘,也不会出现自身的交叉。 输入 输入文件的第一行包含一个表示测试案例数的整数。每一个测试案例包含两行数据。案例的第一行数据是表示封闭路径起止点坐标的两个整数 x 和 y。第二行是一个字符串。串中的每一个字符表示在封闭路径中的一步行进,其中“W”表示向西, “E”表示向东, “N”表示向北, “S”表示向南而“.”表示终止。 输出 对每一个测试案例,输出一行表示案例编号的信息(“Bitmap #1” “Bitmap #2”等)。接下来输出表示位图中 32 行像素的数据。每行表示成一个有 32 个字符的字符串,每个字符表示这一行中的一个像素点。“X”表示路径边界上的像素,“.”表示非路径边界上的像素 输入样例 1 输出样例 Bitmap #1 解题思路 (1)数据的输入与输出 按输入文件格式的描述,首先应当从输入文件中读取案例数 T。然后依次读取每个案例数:第一行包含表示起点坐标的 x 和 y,第二行是一个表示封闭路径从起点开始逆时针行进每一步方向的字符串(以“.”作为结束标志)path。对此路径,模拟从起点(x, y)逆时针方向沿路径行进,画出边界(路径外围的像素点)。把画有路径外围边界的位图数据(二维数组)作为计算结果,将此结果按输出格式(二维数组中的一行数据亦作为一行)逐行写到输出文件中。 其中,第 7 行调用模拟从(x, y)开始沿路径 path 逆时针行进,进而画出路径外围边界的过程 BORDER(path, x, y)是解决一个案例的关键。 (2)处理一个案例的算法过程 将 32×32 的位图表示成矩阵 bitmap[1…32, 1…32],初始化为每一个像素 bitmap[i, j]=“.”。封闭路线 path 从坐标(x, y)开始,沿栅格线逆时针行进。我们要标识的边界总是处于路线的外围,也就是题面中所说的若行进于路线,则边界始终位于行进者右侧(见图 3-2)。这样,向四个不同方向运动时标识边界应该遵循如下规则: 1 向东:在像素(x, y)处做标识“X”,然后 x 增加 1。 按此规律,我们有如下所示的算法的伪代码描述。 算法 3-2 解决“边界”问题一个案例的过程 算法的运行时间取决于第 3~15 行的 while 循环的重复次数。由于,每次重复模拟的是沿路径行进一步(第 2 行 i 初始化为 1,第 15 行 i 自增 1) ,所以该循环的重复次数恰为沿路径行进的步数,也就是 path 的长度 n。循环体中的操作是模拟行进一步,无非就是按行进于路径外围这一规律在 bitmap 合适的位置上填写“X”,耗时必为Θ(1)。于是,算法 3-2 的运行时间为Θ(n),其中 n 为路径 path 的长度。解决本问题的算法的 C++实现代码存储于文件夹 laboratory/Border 中,读者可打开文件 Border.cpp 研读,并试运行之。C++代码的解析请阅读第 9 章 9.1.2 节中程序 9-2 的说明。在现实模拟中常需要根据事物本身的特性,将反映事物属性的数据巧妙地加以组织,可以有效地提高解决问题的算法的时-空效率。常用的数据组织方式有栈—反映数据先进后出规律、 队列—反映数据先进先出规律以及优先队列—反映按数据属性的优先级安排数据使用顺序的规律,等等。甚至,有些事物本身属性数据的描述也可组织成有趣的数据结构。例如数学表达式就可表示成一棵二叉树—父节点表示运算符,子节点表示运算数 所谓“栈”,是线性表的一个变异:数据元素的加入和删除限制在线性表的同一端。最先加入的元素称为“栈底”,最后加入的元素称为“栈顶”,记为 TOP。将元素加入栈的操作称为“入栈”,记为 PUSH。将栈顶元素删除的操作称为“出栈” 若用数组来存储加入栈 S 中的元素,并维护表示栈顶元素下标的属性 top (初始为 0),算法 3-3 描述了几个常用的栈操作 由于将插入和删除操作限制在数组尾部,故所有这些操作的运行时间都是常数Θ(1)。 问题描述 标准的 Web 浏览器包含前后翻页的功能。实现这一功能的方法之一是使用两个栈跟踪网页踪迹,使得通过向后或向前操作可达到指定的页面。本题中,要求你来实现这一目标。需要支持下列指令: BACK:将当前页面压入前进栈。将后退栈栈顶网页弹出,并设其为新的当前网页。若后退栈为空,则忽略本命令。FORWARD:将当前网页压入后退栈。弹出前进栈栈顶网页,并设其为新的当前网页。若前进栈为空,则忽略本指令。VISIT:将当前网页压入后退栈,将 URL 置为新的当前网页。清空前进网页。QUIT:退出浏览器。 假定浏览器初始加载 URL 为 http://www.acm.org/的网页 输入 输入是一系列的指令。指令关键字为 BACK、FORWARD、VISIT 和 QUIT,全部为大写。各 URL 无空白字符且均不超过 70 个字符。 输出 对除了 QUIT 指令以外的每一条命令,若指令未被忽略,执行完指令后输出当前页面的URL。否则,输出“Ignored” 。对每个指令的输出应各占一行。对 QUIT 指令不输出任何信息。 输入样例 VISIT http://acm.ashland.edu/ http://acm.ashland.edu/ 解题思路 (1)数据的输入与输出 根据输入文件的格式,我们应当从输入文件中逐行读取各条指令,直至读到 QUIT。将各条指令(除 QUIT 外)依次存于数组 cmds。调用浏览器模拟过程执行各条指令,并把执行的结果逐条存于数组 result 中。最后,将 result 中的每一个元素作为一行写入输出文件。 其中,第 8 行调用模拟网页浏览器的过程 WEB-NAVIGATION(cmds)是解决一个案例的关键。 (2)处理一个案例的算法过程 根据题面提示,需要维护两个栈 forward-stack 和 back-stack(初始化为空集∅)以及一个表示当前访问的页面地址 current-url(初始化为“http://www.acm.org/”)来模拟网上冲浪时浏览器前后翻页的过程。除了 QUIT,浏览器要响应 3 个操作,即 BACK、FORWARD、VISIT。 利用上述的操作,模拟浏览器进行 Web 导航的过程可描述如下。 算法 3-4 解决“Web 导航”问题的算法过程 设输入文件中指令数为 n。由于三个功能过程 BACK、FORWARD 和 VISIT 只有最后者的重复清栈操作(VISIT 过程中第 3~4 行的 while 循环)耗时Θ(n),其他两个的耗时均为Θ(1)。而 WEB-NAVIGATION 过程中,第 2~15 行的 for 循环重复 n,故其运行时间最多为 n 2,即Θ(n 2) 问题 3-4 周期序列 问题描述 给定函数 f:{0…N}→{0…N}。其中,N 为一个非负整数。对给定的非负整数 n≤N,可以构造一个无穷序列 F = f 1 ( n ) , f 2 ( n ) , . . . , f k ( n ) , . . . F={ f^1 (n), f^2 (n), ..., f^k(n), ...} F=f1(n),f2(n),...,fk(n),...。 其中, f k ( n ) f^k(n) fk(n)定义为 f 1 ( n ) = f ( n ) f^1(n) = f(n) f1(n)=f(n)以及 f k + 1 ( n ) = f ( f k ( n ) ) f^{k+1}(n) = f(f^k(n)) fk+1(n)=f(fk(n))。 不难看出,每一个这样的序列最终都是有周期的。即从某一项开始,往后的数据项都是周而复始,例如{1, 2, 7, 5, 4, 6, 5, 4, 6, 5, 4, 6 , …}。对给定的非负整数 N ≤11000000、n≤N及函数关系 f,要求计算出序列 F 的周期。 输入的每一行包含整数 N 和 n 以及函数 f 的表达式。其中的 f 是以后缀方式给出的,后缀表达式也称为逆波兰表达式(Reverse Polish Notation 缩写为(RPN))。表达式中的运算数是无符号整数常量、表示整数 N 的符号以及变量符号 x。运算符全部都是二元运算,包括:+(加),*(乘)及%(求模,即整数除法的余数) 。运算数与运算符之间用一个空格隔开。运算符%在表达式中仅出现一次,且位于表达式的最后,其第二个运算数必是表示 N 的符号。下列的函数: 2 x * 7 + N % 就是一个 RPN,转换成等价的后缀表达式为(2*x+7)%N。输入中的最后一行 N 的值为 0,它表示输入结束,对于此行数据无需做任何处理。对输入中的每一行,输出一行仅含一个表示对应给定的输入数据行的序列 F 的周期的整数。 输入样例 10 1 x N % 输出样例 1 解题思路 (1)数据的输入与输出 按照输入文件格式,依次处理每个测试案例。文件中的每行表示一个测试案例。其中,开头是两个表示模数和变量 x 的值的整数 N,n。接着是表示逆波兰式的一串符号。将逆波兰式表示成一个字符数组 RPN,对案例数据 N,n,RPN 计算用该表达式构成的序列周期值,将计算所得的结果作为一行写入输出文件。N=0 且 n=0 为输入结束标志。 其中,第 7 行调用计算周期序列最小周期的过程 EVENTUALLY-PERIODIC-SEQUENCE(N, n, RPN),是解决一个案例的关键。 (2)处理一个案例的算法过程 解决这个问题有两个关键点:首先,如何根据表示为串的逆波兰式计算函数值;其次,如何找到序列 f ( x ) , f 2 ( x ) , . . . , f k ( x ) , . . . f(x), f^2(x), ..., f^k(x), ... f(x),f2(x),...,fk(x),...中的最小周期。对于前者,我们可以在分析逆波兰式时,利用一个栈 S 计算出表达式的值。例如,对输入样例中的串“x x 1 + * N %”,图 3-4 展示了计算的过程。 图 3-4 中, (a)分析出式中第 1 个运算数 x,将其压入栈 S; (b)分析到第 2 个运算数 x,压入栈 S;©分析到第 3 个运算数 1,压入栈 S; (d)分析到运算符“+” ,弹出 S 中的两个运算数 1 和 x,相加后压入栈 S; (e)分析到运算符“” ,弹出 S 中的两个运算数 x+1 和 x,相乘后压入 S; (f)分析到运算数 N,压栈; (g)分析到运算符“%”,弹出 S 中的两个运算数 N 和 x(x+1),计算后将所得结果 x*(x+1)%N 压栈。 我们把根据逆波兰式 RPN、自变量值 x 与模 N 计算出 f(x)的过程表示为下列的伪代码。 算法 3-5 计算逆波兰表达式的算法过程 算法的运行时间取决于第 3~17 行的 for 循环重复次数 n。每次重复所执行的 if 分支结构中的任何一个分支,耗时都是Θ(1) (这是因为其中的栈 S 的压栈和弹栈操作耗时均为Θ(1))。所以算法 3-5 的运行时间为Θ(n)。对于后者,我们将 x 初始化为 n,设置一个存放 fk(x)(k=0, 1, …)的集合 A(初始化为∅)。只要 x∉A,将 x 及其序号 k 存于 A。然后利用 CALCULATE 过程,计算 fk+1(x)并赋予 x,k 自增 1 作为下一轮计算的起点。循环往复,直至 x∈A。当前 x 的序号 k 与找到的与之相等的元素之序号 i 的差 k-i 即为 x 值的最小周期,返回。 算法 3-6 解决“周期序列”问题的算法过程 设算法的第 4~8 行的 while 循环重复了 m 次。由于对集合 A 只进行了插入(第 5 行)和查找(第 4 行的条件检测)两种字典操作,故若将 A 表示为散列表,这两个操作均耗时Θ(1)(见表 2-1)。根据上述对算法过程 CALCULATE 的分析,第 7 行耗时为Θ(n)。因此算法的运行时间为Θ(nm)。 所谓队列,也是线性表的一个变异:将元素的插入和删除分别限制在线性表的表尾、表首两端。这样,队列中的数据元素满足先进先出的特性,就像人们排队等待服务那样,如图3-5 所示。将元素加入队列成为队尾的操作称为“入队”,将队首删除的操作称为“出队”。 与栈的操作相似,将入队操作和出队操作分别表示为 PUSH 和 POP。通常用链表来实现队列。此外,还需要维护 3 个属性:队列中的元素个数 n,队首 head,队尾 tail。 由于对链表的两端进行元素的加入与删除都只需常数时间,所以算法 3-7 中的队列的入队操作 PUSH 和出队操作 POP,包括读取队首元素操作 FRONT 的运行时间都是Θ (1)。 问题 3-5 稳定婚姻问题 问题描述 稳定婚姻问题指的是寻求一个集合中的成员按爱慕程度与另一个集合中的成员的对应关系的问题。问题的输入包括: n 个男性组成的集合 M。 n 个女性组成的集合 F。每一个男性和每一个女性都有一张对各异性的爱慕程度表。表中名单按爱慕程度排序,从最喜欢到最不喜欢。婚姻是男性集合到女性集合之间的一个 1-1 对应。婚姻 A 称为是稳定的,若不存在序偶 输入 输入的第一行给定测试案例数 T。每个测试案例的第一行包含一个整数 n (0 < n < 27)。接下来的一行描述 n 个男性和 n 个女性的名字(前 n 个字母)。男性名字表示为小写字母,女性名字表示为大写字母。接下来的 n 行描述每个男性对各女性的爱慕程度。最后的 n 行描述每个女性对各男性的爱慕程度。 输出 对每一个测试案例,输出男性优先的稳定婚姻。测试案例中的各序偶按男性名字字典顺序排列,如输出样例所示。测试案例之间用空行隔开。 输入样例 2 输出样例 a A b B c C a A b B c C 按输入文件的格式描述,首先从中读取案例数 T。然后依次读取每个案例的输入数据。每个案例的第一行数据是表示男女孩各有几个的整数 n,略过表示男女孩标识行。依次读取n 个男孩各自对女孩们的喜欢程度,存入字典 F。依次读取 n 个女孩各自对男孩们的喜欢程度,存入字典 M。对 F 和 M 计算这 n 个男孩和 n 个女孩配合而成的 n 个最稳定婚姻。将计算的结果按男孩们标示符字典顺序,每行一对夫妇写入输出文件,结束前输出一个空行。 其中,第 15 行调用计算稳定婚姻的过程 STABLE-MARRIAGE(M, F)是解决一个案例的关键。 (2)处理一个案例的算法过程 对一个案例数据 F 和 M,使用一个队列 Q 来模拟男女之间的订婚过程。设置一个男孩的求婚队列 Q 和订婚集合 A(初始化为空集)。开始时,所有的男性均进入求婚队列 Q,然后依次让队首男性 m 向自己尚未求过婚的最爱慕女性 f 求婚,若该女性未订婚,则 m,f 订婚, 算法 3-8 解决“稳定婚姻”问题一个案例的算法过程 设男孩数与女孩数均为 n。则最坏情形是每个男孩都要进行 n 次求婚才得到真爱。这样,第 3~12 行的 while 循环将重复Θ (n2)次。每次循环中对队列 Q 的入队、出队和访问队首操作的耗时均为常数Θ(1)。若将 F, M 表示为散列表,则第 5 行在 F 中的查找操作耗时为Θ(1)。若婚约集合 A 表示为二叉搜索树(因为除了要对 A 进行字典操作,输出前还需对其进行排序),则第 7、11 行对其进行的插入操作、第 9 行进行的查找操作以及第 10 行进行的删除操作均耗时Θ(lgn)(见表 2-1)。因此,算法 3-8 的运行时间为Θ (n2lgn)。解决本问题的算法的 C++实现代码存储于文件夹 laboratory/The Stable Marrige 中,读者可打开文件 The Stable Marrige.cpp 研读,并试运行之。C++代码的解析请阅读第 9 章 9.5.3节中程序 9-65~程序 9-67 的说明ENERGY-CONVERSION(N, M, V, K)
A←M, count←0
if A≥N 情形1
then return 0
if A#include 问题 1-4 美丽的花园
描述
1 3
3 7
1 4打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取案例数 F,K
创建数组 L[1..K],I[1..K]
for i←1 to K
do 从 inputdata 中读取案例数据 L[i], I[i]
result← THE-FLOWER-GARDEN(F, K, L, I)
将 result 作为一行写入 outputdata 中
关闭 inputdata
关闭 outpudata
THE-FLOWER-GARDEN(F, K, L, I)
i←MIN-ELEMENT(L) 最先开始栽种花的坑
count←i-1 之前的坑当然是空的
while i≤F 逐一考察以后的每个坑
do for j←1 to K 逐一考察每一种花
do if i-1 Mod I[j]≡L[j] 查看第 i 个坑是否栽上第 j 种花
then break this loop
if j>K 若 i 号坑没有种上任何花
then count←count+1 空坑计数器增加
i ←i+1
return count
#include 简单的数学计算
问题 1-5 小小度刷礼品
6打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取案例数 T
for t←1 to T
do 从 inputdata 中读取案例数据 x, a, b
result← GIFT(x, a, b)
将 result 作为一行写入 outputdata 中
关闭 inputdata
关闭 outpudata
GIFT (x, a, b)
t← x 的 10 进制位数
m←10^t
count ←0
for i ←a to b
do if i Mod m=x
then count ←count+1
return count
m←1while m<x do m←m*10
GET-GIFT(x, a, b)
t← x 的 10 进制位数
m←10t
ar ←a Mod m,aq←a/m
br ←b Mod m,bq←b/m
if ar>x
then aq←aq+1
if br<x
then bq←bq-1
return b q-aq+1
#include 问题 1-6 找到牛妞
5 17
3 21
6打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取案例数 T
for t←1 to T
do 从 inputdata 中读取案例数据 N, K
result←CATCH-THAT-COW(N, K)
将 result 作为一行写入 outputdata 中
关闭 inputdata
关闭 outpudata
CATCH-THAT-COW(N, K)
if N≥K
then return N-K
p←max{i|2i≤K}, q←max{i|2iN≤K}, t←max{i|2i≤N}
if N2q=K
then return q
a← q+K-N2q , b← q+1+ N2q+1-K, c←(N-2t)+(p-t)+(K-2p)
d←(N-2t)+(p-t+1)+(2p+1-K), e←(2 t+1 -N)+(p-t+1)+(K-2 p ), f ←(2t+1-N)+(p-t)+(2p+1 -K)
return min{a, b, c, d, e, f}
#include 问题 1-7 糟糕的公交调度
100 200 300
400 500 600
700 800 900
1000
END
START 3
100 200 300 4 3 2 4 2 22
800
10 1000
32767
END
ENDOFINPUT
20打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取一行到 s
while s≠"ENDOFINPUT"
do 略过 s 中的"START",并读取 N
创建数组 durations[1..N]
for i←1 to N
do 从 inputdata 中读取一行到 s
将 s 中的每一个整数数据添加到 durations[i]中
从 inputdata 中读取 arrival
result←WORLD-WORST-BUS-SCHEDULE(durations, arrival)
将 result 作为一行写入 outputdata
在 inputdata 中略过一行"END"
从 inputdata 中读取一行到 s
关闭 inputdata
关闭 outpudata
#include 问题 1-8 冒泡排序
( 1 5 4 2 8 ) −> ( 1 4 5 2 8 ),交换,因为 5 > 4。
( 1 4 5 2 8 ) −> ( 1 4 2 5 8 ),交换,因为 5 > 2。
( 1 4 2 5 8 ) −> ( 1 4 2 5 8 )由于这两个元素已经保持顺序(8>5)
,算法不对它们进行交换。
第二趟操作:
( 1 4 2 5 8 ) −> ( 1 2 4 5 8 ),交换,因为 4 > 2。
( 1 2 4 5 8 ) −> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) −> ( 1 2 4 5 8 )
第一行含有一个表示案例数的整数 T (T≤100 000)。
跟着的是 T 行表示各案例的数据。
每行包含两个整数 N 和 K(1≤ N≤1,000,000, 0≤ K ≤ N−1),其中 N 表示序列长度而 K 表示对序列进行冒泡排序的趟数。
3
2#include 图的性质
定义 1-1
∑ i = 1 n = 2 m \sum^n_{i=1} = 2m i=1∑n=2m
即所有顶点的度数之和为边数的 2 倍问题 1-9 聚会游戏
5 4 2 3 2 5
7
3 4 2 2 2 3
0
Maybe truth打开输入文件 inputdata创建输出文件 outputdatawhile N≠0 do 创建数组 a[1..N] for i←1 to N-1 do 从 inputdata 中读取 a[i]a[N] ←N-1 Robin 认识每个人result← PARTY-GAME(a)if result=true then 将"Maybe truth"作为一行写入 outputdata else 将"Lie absolutely"作为一行写入 outputdata从 inputdata 中读取案例数据 N关闭 inputdata关闭 outpudata
PARTY-GAME(a)n←length[a]count←0for i←1 to n Z检测每一个人报告的认识人数 do if a[i] is odd then count←count+1return count is even
利用握手定理判断晚会中是否有客人说谎的过程#include 3
2 3 1
6
4 3 1 5 2 6
0
18打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取人数 N
while N≠0
do 创建数组 a[1..N]
for i←1 to N
do 从 inputdata 中读取 a[i]
result←COW-SORTING(a)
将 result 作为一行写入 outputdata
从 inputdata 中读取案例数据 N
关闭 inputdata
关闭 outpudata
COW-SORTING(a)
n←length[a], count←0
copy a to b
SORT(b)
amin←b[1]
while n>0
do j←a 中首个非 0 元素下标
ti←∞, sum←a[j]
k←1, ai←a[j]
a[j]←0, n←n-1
while b[j]≠ai
do k←k+1
sum←sum+b[j]
if ti>b[j]
then ti←b[j]
j←FIND(a, b[j])
a[j]←0, n←n-1
if k>1
then count←count+sum+min{(k-2)*ti, (k+1)*amin}
return count
#include 数据集合与信息查找
集合及其字典操作
tthumb
LIVESPACE BLOGJAM
hilton
paeinstein
YOUBOOK
j97lee
sswxyzy
j97lee
paeinstein
SKINUX
1
0
LIVESPACE BLOGJAM 1
UBQTS TXT 1
SKINUX 0打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取一行到 s
while s≠"0"
do 创建空集合 a
while s≠"1"
do APPEND(a, s)
从 inputdata 中读取一行到 s
p←OPEN-SOURCE(a)
for each project∈p
do 将"name[project] number[project] "作为一行写入 outputdata
从 inputdata 中读取一行到 s
关闭 inputdata
关闭 outputdata
OPEN-SOURCE(a) Z处理一个案例Projects←∅, Students←∅n←length[a], i←1while i≤n do project←<a[i], 0> i←i+1 while a[i]为学生签名 处理 1 个项目 do userid←a[i] student←FIND(Students, userid) if student∉Students 签名为 userid 的学生是第一次出现 then INSERT(Students, < userid, project.name, false>) number[project]←number [project] +1 else if pname[student] ≠ name[project] and deleted [student]=false then deleted[student]←true p←FIND(Projects, pname[student]) DELETE(Projects, p) Z在 projects 中删除元素 number[p]← number [p]-1 修改人数 INSERT(Projects, p) 重新加入i←i+1INSERT(Projects, project)SORT(Projects)return Projects
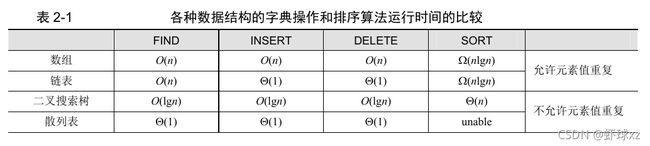
各种数据结构的字典操作和排序算法运行时间的比较#include 问题 2-2 王子的难题
2 对指定的小格减去一数。
3 查询从格子(x1,y1,z1)到格子(x2,y2,z2)所有数的和。
(x1≤x2, y1≤y2, z1≤z2)
作为 Ray 的好朋友,又是一个优秀的程序员,你要为 Ray 写一个程序应答所有的查询,
帮助 Ray 与他的梦中情人喜结良缘。
输入的第一行包含一个整数 n(1≤n≤100),表示魔方的尺寸。然后有若干行格式如下的数据:
A x y z num:表示在格子(x, y, z)加入一数 num。
S x y z num:表示在格子(x, y, z)减去一数 num。
Q x1 y1 z1 x2 y2 z2:表示查询从(x1, y1 , z1)到(x2 , y2 , z2)的格子中数的总和。
所有查询中涉及的数均不会超过 1000000。输入文件以一行仅含 0 的数据结束,对这个
0 不需要做任何处理。
A 1 1 4 5
A 2 5 4 5
Q 1 1 1 10 10 10
S 3 4 5 34
Q 1 1 1 10 10 10
0
-24
按本题输入文件格式描述,需先从输入文件读取魔方规模n。然后读取各行指令,将指令存储于串数组 a 中,直至读到仅含“0”的一行为止。计算执行 a 中各条指令对魔方中各格子中数据的影响,并将执行查询指令的查询结果记录于数组 result 中。将 result 中的元素按每行一个写入输出文件中。打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 n
从 inputdata 中读取一行 s
创建数组 a
while s≠"0"
do APPEND(a, s)
从 inputdata 读出一行 s
result←PRINCE-RAY-PUZZELE(a)
for each x∈result
do 将 x 作为一行写入 outputdata
关闭 inputdata
关闭 outputdata
sum←0
for x←x 1 to x2
do for y←y1 to y2
do for z←z1 to z2
do sum←sum+BRICK[x, y, z]
output sum
PRINCE-RAY-PUZZELE(a)
BRICK←∅, result←∅
m←length[a]
for i←1 to m
do read command from a[i]
if command="A" or "S" 加指令或减指令
then read <x, y, z, num> from a[i]
cell←FIND(BRICK, <x, y, z >)
if cell∉BRICK
then if command ="A"
then APPEND(BRICK, <x, y, z, num>)
else APPEND(BRICK, <x, y, z, - num>)
else if command ="A"
then number[cell] ← number[cell] +num
else number[cell] ← number[cell] -num
else read x1, y1, z1, x2, y2, z2 from a[i] Z查询指令 Q
sum←0
for each <x, y, z, number> ∈BRICK Z遍历 BRICK
do if x1≤x≤x2 and y1≤y≤y2 and z1≤z≤z2
then sum←sum+number
APPEND(result, sum)
return result
#include
#include
问题 2-3 度度熊就是要第一个出场
4 6 3
1 2 1
1 2 4
1 2 6
2 3 2
2 3 5
3 4 4
4 0 3
No打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 T
for i←1 to T
do 从 inputdata 中读取 N, M, K
创建数组 a
for j←1 to M
do 从 inputdata 中读取 xl,xr,y
APPEND(a, 问题 2-4 寻找克隆人
AAAAAA
ACACAC
GTTTTG
ACACAC
GTTTTG
ACACAC
ACACAC
TCCCCC
TCCCCC
0 0
2
0
1
0
0
0
0
0打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 n 和 m
while n>0 and m>0
do 创建数组 a[1..n]
for i←1 to n
do 从 inputdata 中读取 a[i]
solution←FIND-THE-CLONES(a)
for each s∈solution
do 将 s 作为一行写入 outputdata 中
从 inputdata 中读取 n 和 m
关闭 inputdata
关闭 outputdata
FIND-THE-CLONES(a)
n←length[a], DNAS←∅
for i←1 to n
do dna←a[i]
sample←FIND(DNAS, dna)
if sample ∉DNAS
then INSERT(DNAS, <dna, 1>)
else copies[sample]←copies[sample]+1
solution[1..n]←{0, 0, ..., 0}
for each sample∈DNAS
do solution[copies[sample]]←solution[copies[sample]]+1
return solution
#include
程序对每个测试案例仅输出一行仅含一个表示文本中长度为 N 的不同子串个数的整数的数据。
daababac
0 0打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 N 和 NC
while N>0 or NC>0
do 从 inputdata 中读取文本行 text
result← CRAZY-SEARCH(text, N)
将 result 作为一行写入 outputdata
从 inputdata 中读取 N 和 NC
关闭 inputdata
关闭 outputdata
CRAZY-SEARCH(text, N)
length←text 的长度
S←∅
for i←0 to length-N
do s←text[i...i+N-1]
t←FIND(S, s)
if t∉S
then INSERT(S, s)
return S 的元素个数
#include 文本串的查找

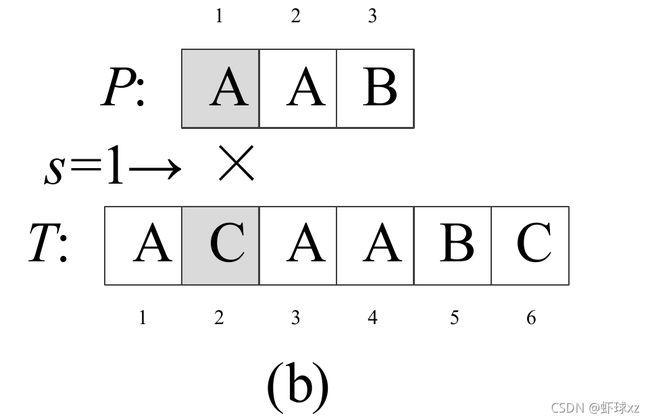
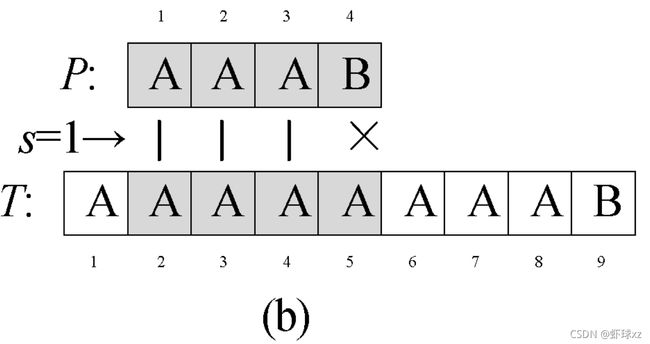
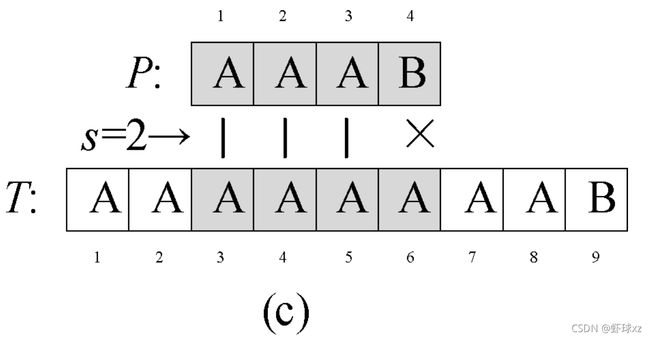
STRING-MATCHER(T, P)
n ← length[T]
m ← length[P]
for s ← 0 to n - m
do k←1
while P[k] = T[s + k]
do k←k+1
if k>m
then return s
return -1
问题 2-6 Pandora 星球上的计算机病毒
则程序还原为 ABDDEKKKKKKKG。
程序无论是否压缩,其长度至少为 1,至多为 5 100 000。
输出
对每一个测试案例,输出一行表示该程序被感染的病毒数目的整数 K。
输入样例
2
AB
DCB
DACB
3
ABC
CDE
GHI
ABCCDEFIHG
4
ABB
ACDEE
BBB
FEEE
A[2B]CD[4E]F
3
2打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 T
for t←1 to T
do 从 inputdata 中读取 n
创建数组 virus[1..n]
for i←1 to n
do 从 inputdata 中读取 virus[i]
从 inputdata 中读取 program
result←COMPUTER-VIRUS-ON-PLANET-PANDORA(virus, program)
将 result 作为一行写入 outputdata
关闭 inputdata
关闭 outputdata
COMPUTER-VIRUS-ON-PLANET-PANDORA(virus, program)
n←length[virus]
count←0
program1 ← EXTRACT(program)
for i←1 to n
do virus1←virus[i]的逆串
if STRING-MATCHER(program 1 , virus[i])>-1 or STRING-MATCHER(program1 , virus 1 )
then count←count+1
return count
EXTRACT(program)
program1 ←∅, i←1
N←length[program]
while i≤N 扫描 program
do while i≤N and program[i]≠‘[’ 复制非压缩内容
do APPEND(program1, program[i])
i←i+1
if i>N
then return program
i←i+1, q←0 遇到压缩符
while program[i]为数字 a
do q←q*10+a
i←i+1
x←program[i]
str←q 个 x 组成串
APPEND(program1, str)
i←i+1
return program1
#include 全序集序列的排序
T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n)=2T(n/2)+Θ(n) T(n)=2T(n/2)+Θ(n)
在上式中,将Θ(n)简化为 n,并不影响 T(n)渐进式的表示。即上式可表示成
T ( n ) = 2 T ( n / 2 ) + n T(n)=2T(n/2)+n T(n)=2T(n/2)+n问题 2-7 DNA 排序
AACATGAAGG
TTTTGGCCAA
TTTGGCCAAA
GATCAGATTT
CCCGGGGGGA
ATCGATGCAT
AACATGAAGG
GATCAGATTT
ATCGATGCAT
TTTTGGCCAA
TTTGGCCAAA打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 n 和 m
for i←1 to m
do 创建数组 DNAS[1..m]
从 inputdata 中读取一行到 DNAS[i]
DNA-SORTING(DNAS)
for i←1 to m
do 将 DNAS[i]作为一行写入 outpudata
关闭 inputdata
关闭 outputdata
INVERSION(dna)
n←length[dna], count←0
cC←0,cG←0,cT←0
for i←1 to n
do if dna[i]= "A"
then count←count+(cC + cG + cT)
else if dna[i]= "C"
then count←count+(cG + cT)
cC←cC+1
else if dna[i]= "G"
then count←count+ cT
cG ← cG +1
else cT ← cT +1
return count
DNA-SORTING(DNAS)m ←length[DNAS]创建集合 afor i←l to m do inv[DNAS [i]]←INVERSION(string[DNAS [i]])SORT(DNAS
#include 问题 2-8 度度熊的礼物
接下来 n 行每行两个整数表示度度熊好朋友的两种属性 Xi,Yi。
接下来两行,每行三个整数 ki,Ai 和 Bi,表示度度熊拥有第 i 种超级礼物的个数与属性值。1≤n≤1000,0≤Xi,Yi,Ai,Bi≤1000,0≤ki≤n,保证 k1+k2≥n。
输出
3 6
7 4
1 5
2 4
3 3 4
3 4 3打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 n
创建数组 X[1..n]和 Y[1..n]
for i←1 to n
do 从 inputdata 中读取 X[i]和 Y[i]
从 inputdata 中读取 k1,A1,B1
从 inputdata 中读取 k2,A2,B2
result←GIFTS(X, Y, k1, A1, B1, k2, A2, B2)
将 result 作为一行写入 outputdata
关闭 inputdata
关闭 outputdata
GIFTS(X, Y, k1, A1, B1, k2, A2, B2)
n←length[X]
S1←∅, S2←∅
for i←1 to n
do if A1X[i]+B1Y[i]>A2X[i]+B2Y[i]
then INSERT(S1, <A1X[i]+B1Y[i], i>)
INSERT(S2, <A2X[i]+B2Y[i], i>)
n1←length[S1], n2←length[S2]
if n1>k1
then SORT(S1)
将 S1 中末尾的 n1-k1 个元素移除并将这些元素对应的第 2 种礼物开心值加入 S2
else if n2>k
then SORT(S2)
将 S2 中末尾的 n2-k2 个元素移除并将对应的第 1 种礼物开心值加入 S1
return S1 中的开心值之和+S2 中的开心值之和
#include 题 2-9 通信系统
3
3 100 25 150 35 80 25
2 120 80 155 40
2 100 100 120 110打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 T
for t←1 to T
do 从 inputdata 中读取 n
创建数组 devices[1..n],并对每一个 k,创建 devices[k]←∅
创建集合 bands←∅
for i←1 to n
do 从 inputdata 中读取 mi
for j←1 to mi
do 从 inputdata 中读取(b, p)
INSERT(devices[i], (b, p))
INSERT(bands, b)
result←COMMUNICATION-SYSTEM(devices, bands)
将 result 以小数点三位的精度按一行写入 outputdata
关闭 inputdata
关闭 outputdata
COMMUNICATION-SYSTEM(devices, bands)
n←length[devices], r←0
for i←1 to n
do SORT(devices[i])
for each B∈bands 考察每一个可能的带宽
do P←0
for i←1 to n 考察每一种设备
do pmin←∞
for each (b, p) ∈devices[i]对第 i 种设备的带宽不小于 B 的供应商的数据
do if b<B 由 devices[i]的降序排列,无需再考虑后面的数据
then break this loop
if p<pmin 跟踪符合条件的最小价格
then pmin←p
if pmin=∞ 没有符合带宽不小于 B 这一条件的设备
then break this loop
P←P+pmi
if i≤n 没有符合带宽不小于 B 这一条件的设备
if r<B/P
then r←B/P
return r
#include 集合的并、交、差运算
INTERSECTION(A, B) 集合 A 与 B 的交
C←∅
for each x∈A
do if x∈B
then INSERT(C, x)
return C
DIFFERENCE(A, B) 集合 A 与 B 的差
C←∅, T←INTERSECTION(A, B)
for each x∈A
do if x∉T
then INSERT(C, x)
return C
UNIN(A, B) 集合 A 与 B 的并
T←INTERSECTION(A, B) , C←DIFFERENCE(B, T)
for each x∈A
do INSERT(C, x)
return C
计算集合并、交、差的算法过程问题 2-10 计算机调度
0 0 0
1 0 1
2 0 2
3 0 3
4 1 0
5 1 1
6 1 2
7 1 3
8 2 2
9 3 2
0打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 n
while n≠0
do 从 inputdata 中读取 m 和 k
创建数组 i[1..k],x[1..k],y[1..k]
for j←1 to k
do 从 inputdata 中读取 i[j],x[j],y[j]
result←MACHINE-SCHEDULE(n,m,i,x,y)
将 result 作为一行写入 outputdata
从 inputdata 中读取 n
关闭 inputdata
关闭 outputdata
m,i,x,y)是解决一个测试案例的关键。MACHINE-SCHEDULE(n,m,i,x,y)
创建数组 mode[0..n+m-1]←{∅, ∅, ..., ∅}
k←length[x], jobs←∅
for j←0 to k-1
do INSERT(mode[x[j]], i[j])
INSERT(mode[n+y[j]], i[j])
INSERT(jobs, j)
R←mode[0],mode[n]中基数较大者
num←0
while jobs≠∅
do num←num+1
jobs←jobs-R
for j←0 to n+m-1
do mode[j]←mode[j]-R
R←mode[0..n+m-1]中基数最大者
return num
#include 问题 3-1 对称排序
对每一个测试案例,先输出一行“SET n”,其中 n 从 1 开始取值,表示案例序号。接着是 n 行名字输出,如输出样例所示。
输入样例
Bo
Pat
Jean
Kevin
Claude
William
Marybeth
6
Jim
Ben
Zoe
Joey
Frederick
Annabelle
5
John
Bill
Fran
Stan
Cece
0
输出样例
SET 1
Bo
Jean
Claude
Marybeth
William
Kevin
Pat
SET 2
Jim
Zoe
Frederick
Annabelle
Joey
Ben
SET 3
John
Fran
Cece
Stan
Bill打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 n
num←1
while n>0
do 创建序列 names←∅
for i←1 to n
do 从 inputdata 中读取一行到 name
INSERT(names, name)
SYMMETRIC-ORDER(names)
将"SET num"作为一行写入 outputdata
for each name in names
do 将 name 作为一行写入 outputdata
从 inputdata 中读取 n
关闭 inputdata
关闭 outpudata
SYMMETRIC-ORDER(names)
n←length[names]
if n 为偶数
then m←⎣n/2⎦
else m←⎣n/2⎦+1
i←2, j←n+1
while i≤m
do name←names[i]
将 name 插入到 names[j]之前
DELETE(names, name)
i←i+1, j←j-1
#include
#include
2 1
EENNWNENWWWSSSES.
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
.XXX…
X…X…
X…X…
X…X…
.X…X…
…XX…打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取 T
for t←1 to T
do 从 inputdata 中读取 x, y
从 inputdata 中读取一行到 path
bitmap←BORDER(path, x, y)
将"Bitmap # i"作为一行写入 outpudata
for i←1 to 32
do 将 bitmap[i]作为一行写入 outputdata
关闭 inputdata
关闭 outpudata
2 向西:x 减少 1,然后在像素(x, y+1)处做标识“X”。
3 向北:y 增加 1,然后在像素(x, y)处做标识“X”。
4 向南:在像素(x−1, y)处做标识“X”,然后 y 减少 1。BORDER(path, x, y)
创建位图数组 bitmap[1..32]并将每个元素初始化为串".............................."
i←1
while path[i]≠ "."
do if path[i]= "E"
then bitmap[y][x] ←"X"
x←x+1
else if path[i]= "W"
then x←x-1
bitmap[y+1][x] ←"X"
else if path[i]= "N"
then y←y+1
bitmap[y][x] ←"X"
else bitmap[y][x-1] ←"X"
y←y-1
i←i+1
return bitmap
#include 栈及其应用
,记为 POP。如图 3-3 所示。TOP(S)
if S ≠∅
then return S[top[S]]
else return NIL
PUSH(S, e)
top[S]← top[S]+1
S[top[S]]←e
POP(S)
if S ≠∅
then top[S]← top[S]-1
问题 3-3 Web 导航
VISIT http://acm.baylor.edu/acmicpc/
BACK
BACK
BACK
FORWARD
VISIT http://www.ibm.com/
BACK
BACK
FORWARD
FORWARD
FORWARD
QUIT
输出样例
http://acm.baylor.edu/acmicpc/
http://acm.ashland.edu/
http://www.acm.org/
Ignored
http://acm.ashland.edu/
http://www.ibm.com/
http://acm.ashland.edu/
http://www.acm.org/
http://acm.ashland.edu/
http://www.ibm.com/
Ignored打开输入文件 inputdata
创建输出文件 outputdata
创建数组 cmds←∅
从 inputdata 中读取一行到 cmd
while cmd≠"QUIT"
do INSERT(cmds, cmd)
从 inputdata 中读取 cmd
result←WEB-NAVIGATION(cmds)
for each r∈result
do 将 r 作为一行写入 outpudata
关闭 inputdata
关闭 outpudata
BACK ( )
if back-stack≠∅
then PUSH(forward-stack, current-url)
current-url←TOP(back-stack)
POP(back-stack)
return true
return false
FORWARD( )
if forward-stack≠∅
then PUSH(back-stack, current-url)
current-url←TOP(forward-stack)
POP(forward-stack)
return true
return false
VISIT(url)
PUSH(back-stack, current-url)
current-url←url
while forward-stack≠∅
do POP(forward-stack)
WEB-NAVIGATION(cmds)
n←length[cmds], result←∅
forward-stack←∅, back-stack←∅
current-url←"http://www.acm.org/"
for i ←1 to n
do 从 cmds[i]中解析出指令符 cmd
aline←"Ignored"
if cmd="BACK" and BACK()=true
then aline←current-url
else if command="FORWARD" and FORWARD()=true
then aline←current-url
else if command="VISIT"
then 从 cmds[i]解析出参数 url
VISIT(url)
aline←current-url
INSERT(result, aline)
return result
#include
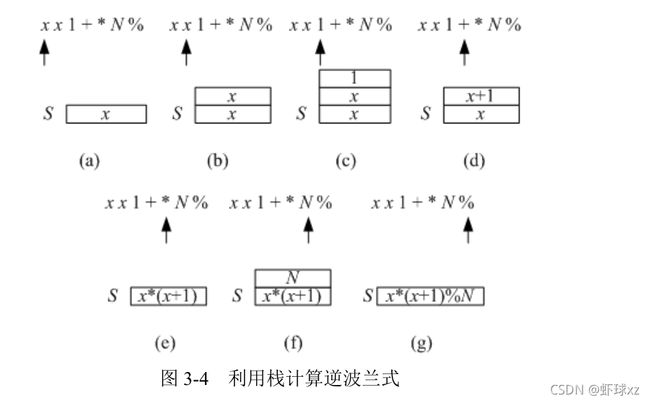
11 1 x x 1 + * N %
1728 1 x x 1 + * x 2 + * N %
1728 1 x x 1 + x 2 + * * N %
100003 1 x x 123 + * x 12345 + * N %
0 0 0 N %
3
6
6
369打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取一行 s
从 s 中解析出 N 和 n
while N>0 or n>0
do 将 s 中剩下的符号作成字符串 RPN
result←EVENTUALLY-PERIODIC-SEQUENCE(N, n, RPN)
将 result 作为一行写入 outputdata
从 inputdata 中读取一行到 s
从 s 中解析出 N 和 n
关闭 inputdata
关闭 outpudata
CALCULATE(N, x, RPN)
S←∅ 设置空栈
n←length[RPN]
for i←1 to n
do if RPN[i]∈{'+', '*', '%'} 若是运算符
then op2←POP(S) 从栈 S 中弹出第 2 个运算数
op1←POP(S) 从栈 S 中弹出第 1 个运算数
if RPN[i]='+' 若运算符为"+"
then PUSH(S, op1+op2) 计算两数之和并压入栈中
else if RPN[i]='*' 若运算符为"*"
then PUSH(S, op1*op2) 将两数之积压栈
else PUSH(S, op1%op2) 运算符为"%"
else if RPN[i]= 'x'
then PUSH(S, x) 是运算数 x
else if RPN[i]= 'N'
then PUSH(S, N) 是运算数 N
else d←RPN[i] 是一般的运算数, 转换为整数
PUSH(S, d)
return POP(S)
EVENTUALLY-PERIODIC-SEQUENCE(N, n, RPN)
k←0
创建集合 A←∅
x←n
while x∉A
do INSERT(A, (x, k))
k←k+1
x← CALCULATE(N, x, RPN)
i ← x 在 A 中的序号
return k-i
#include 队列及其应用
PUSH(Q, e)
crate node x with value e
next[tail]←x
next[tail]←NIL
tail←x
POP(Q)
if Q≠∅
then head← next[head]
FRONT(Q)
return head
3
a b c A B C
a:BAC
b:BAC
c:ACB
A:acb
B:bac
C:cab
3
a b c A B C
a:ABC
b:ABC
c:BCA
A:bac
B:acb
C:abc打开输入文件 inputdata
创建输出文件 outputdata
从 inputdata 中读取案例数 T
for t←1 to T
do 从 inputdata 中读取男孩、女孩数 n
略过 inputdata 中男孩、女孩表示行
创建字典 F←∅
for i←1 to n
do 从 inputdata 中读取男孩表示 f,和对女孩的喜欢程度 preference
INSERT(F, (f, preference))
创建字典 M←∅
for i←1 to n
do 从 inputdata 中读取男孩表示 m,和对男孩的喜欢程度 preference
INSERT(M, (m, preference))
A←STABLE-MARRIAGE(M, F)
SORT(A)
for each couple∈A
do 将 couple 作为一行写入 outputdata
向 outputdat 写入一个空行
关闭 inputdata
关闭 outpudata
STABLE-MARRIAGE(M, F)
A←∅ 婚姻集合
Q←M 求婚队列
while Q≠∅
do m←FRONT(Q) m 为队首
f←F 中 m 未曾追求过且为 m 爱慕度最高者
if f 单身
then INSERT(A, <f, m>) f, m 订婚
POP(Q) m 出队
else if <f, m'>∈A and f 更爱慕 m
then DELETE(A, <f, m'>) f, m'解除婚约
INSERT(A, <f, m>) f, m 订婚
POP(Q) m 出求婚队列
PUSH(Q, m') m'重入求婚队列
return A
#include