拉格朗日插值求具体值点+画图python
文章目录
- 问题
- 拉格朗日插值
- 探索
问题
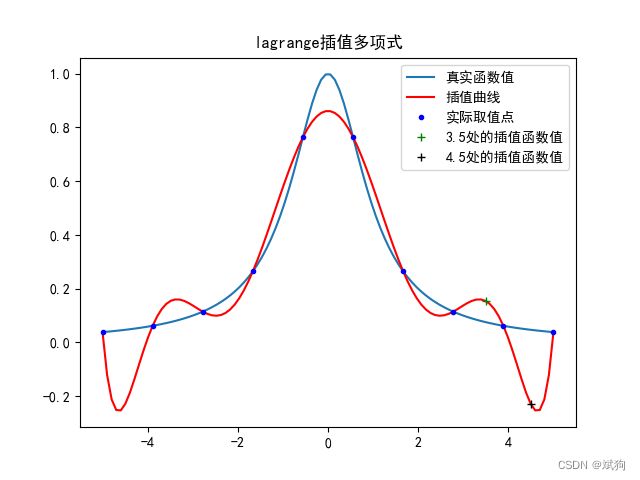
在[-5,5]内取n=10, 按等距节点求n次lagrange插值多项式
取100点,画出插值多项式和原函数的对比图。 并分别比较在x=3.5,x=4.5处的值。
拉格朗日插值
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['sans-serif'] # 显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def fun(x):
return 1/(1+x**2)
def lagrange(x0, y0, x):
n = x0.shape[0]
s = 0
for k in range(0, n):
p = 1
for j in range(0, n):
if k != j:
p = p*(x-x0[j])/(x0[k]-x0[j])
s += p*y0[k]
f = s
return f
x0 = np.linspace(-5, 5, 10) # 在[-5,5]内取n=10, 按等距节点求n次
y0 = fun(x0) # 真实的函数值
x1 = np.linspace(-5, 5, 100) # 为画图取得的100个点
y1 = lagrange(x0, y0, x1) # 将100个点带入10插值多项式得出对应的函数值
f1 = lagrange(x0, y0, 3.5) # 3.5处的插值
f2 = lagrange(x0, y0, 4.5) # 4.5处的插值
plt.figure()
plt.title('lagrange插值多项式')
plt.plot(x1, fun(x1)) # 真实函数的曲线
plt.plot(x1, y1, 'r') # 插值曲线
plt.plot(x0, y0, 'b.') # 插值点
plt.plot(3.5, f1, 'g+') # 两个特殊值点
plt.plot(4.5, f2, 'k+')
plt.legend(['真实函数值', '插值曲线', '实际取值点', '3.5处的插值函数值', '4.5处的插值函数值'])
plt.show()
print('3.5插值结果:', f1, '实际结果:', fun(3.5))
print('4.5插值结果:', f2, '实际结果:', fun(4.5))
探索
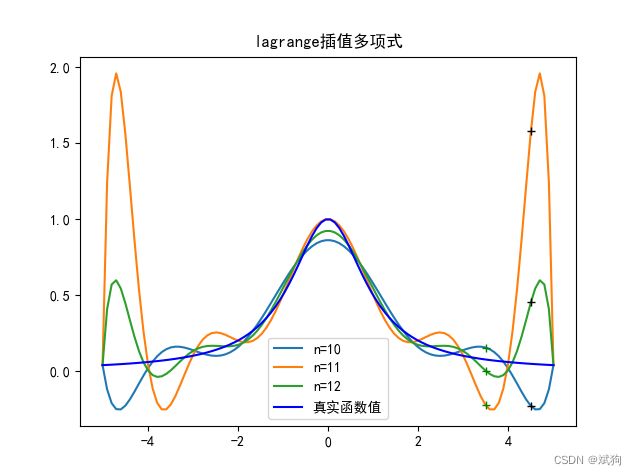
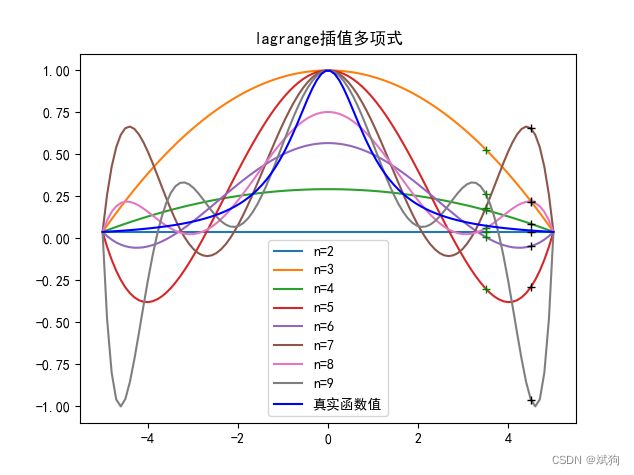
当取得的插值多项式的点的数量不同时,得到的函数曲线也有所不同
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.family'] = ['sans-serif'] # 显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def fun(x):
return 1/(1+x**2)
def lagrange(x0, y0, x):
n = x0.shape[0]
s = 0
for k in range(0, n):
p = 1
for j in range(0, n):
if k != j:
p = p*(x-x0[j])/(x0[k]-x0[j])
s += p*y0[k]
f = s
return f
# 当n的数量为10,11,12时,图像
for i in range(10,13):
x0 = np.linspace(-5, 5, i) # 在[-5,5]内取n=10, 按等距节点求n次
y0 = fun(x0) # 真实的函数值
x1 = np.linspace(-5, 5, 100) # 为画图取得的100个点
y1 = lagrange(x0, y0, x1) # 将100个点带入10插值多项式得出对应的函数值
f1 = lagrange(x0, y0, 3.5) # 3.5处的插值
f2 = lagrange(x0, y0, 4.5) # 4.5处的插值
#plt.figure()
plt.plot(x1, y1,label=f'n={i}') # 插值曲线
#plt.plot(x0, y0, '.',label='实际取值点') # 插值点
plt.plot(3.5, f1, 'g+') # 两个特殊值点
plt.plot(4.5, f2, 'k+')
plt.legend()
#plt.legend( ,'3.5处的插值函数值' , '4.5处的插值函数值'])
plt.title('lagrange插值多项式')
plt.plot(x1, fun(x1),'b',label='真实函数值') # 真实函数的曲线
plt.legend()
plt.show()