学python的第十一天---小蓝(2)
- 一、42点(递推)
- 二、数的计算(递归、递推)
-
- 写法一:递归
- 写法二:递推
- 三、数的划分
-
- 写法一:递归
- 写法二:动态规划
- 四、耐摔手机(难)
-
- 写法一:递推
- 写法二:递归
- 五、搜索
-
- N皇后
- 路径之谜
-
- 写法一:
- 写法二:
- 长草
- 走迷宫
一、42点(递推)
c=input().split()
a=[0]*10
ans=[[]for i in range(10)]
for i in range(6):
if c[i]=='A':
a[i]=1
elif c[i]=='J':
a[i]=11
elif c[i]=='Q':
a[i]=12
elif c[i]=='K':
a[i]=13
else:
a[i]=ord(c[i])-ord('0')
#a[i]=int(c[i])
ans[0].append(a[0])
for i in range(1,6):
for j in range(len(ans[i-1])):
ans[i].append(ans[i-1][j]+a[i])
ans[i].append(ans[i-1][j]-a[i])
ans[i].append(ans[i - 1][j] * a[i])
ans[i].append(int(ans[i - 1][j] / a[i]))
flag=0
for j in range(len(ans[5])):
if ans[5][j]==42:
flag=1
break
if flag==1:
print("Yes")
else:print("No")
二、数的计算(递归、递推)
写法一:递归
n=int(input())
res=1
def f(n):
global res
for i in range(1,n//2+1):
res+=1
f(i)
f(n)
print(res)
写法二:递推
f(4)=f(4/2=2)+f(2/2=1)+1
f(5)=f(5/2=2)+f(2/2=1)+1
…
f(n)=f(n/2)+f(n/2/2)…+f(1)+1
故我们从f(1)开始往前推
n=int(input())
f=[0 for i in range(1000)]
for i in range(1,n+1):
for j in range(1,i//2+1):
f[i]=f[i]+f[j]
f[i]+=1#加上其本身
print(f[n])
三、数的划分
写法一:递归
n,k=map(int,input().split())
def f(n,m):#将n个数化成m份
if n<=0 or m<=0 or n<m:
return 0
if m==1 or m==n:
return 1
return f(n-m,m)+f(n-1,m-1)
ans=f(n,k)
print(ans)
写法二:动态规划
n,k=map(int,input().split())
dp=[[0 for j in range(210)]for i in range(210)]
for i in range(1,n+1):
dp[i][1]=1
dp[i][i]=1
for i in range(3,n+1):
for j in range(2,k+1):
if i>j:
dp[i][j]=dp[i-j][j]+dp[i-1][j-1]
print(dp[n][k])
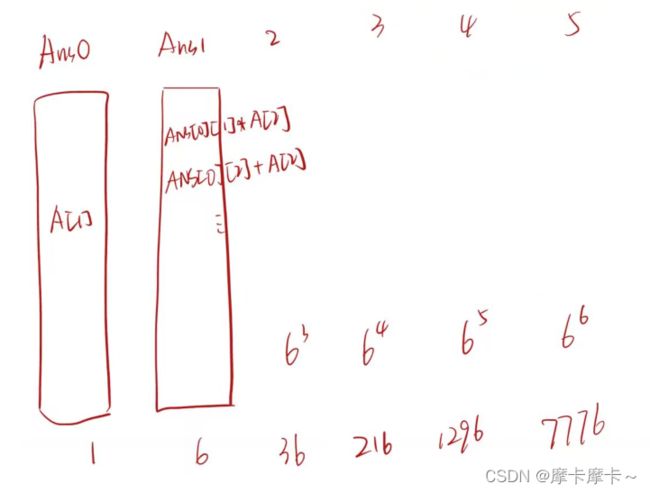
四、耐摔手机(难)
写法一:递推
这一题依旧是有两种写法
a[i]表示一部手机测i次,b[i]表示两部手机测i次,c[i]表示三部手机测i次
b=[0]*105
c=[0]*105
n=int(input())
i=0
while c[i]<n:#表示三部手机是否测到了他的耐摔指数
i+=1
b[i]=i+b[i-1]#其实也就是i-1+b[i-1]+1#坏了就是i次,没坏就是b[i-1]次
c[i]=c[i-1]+b[i-1]+1#同理
print(i)
写法二:递归
f=[[0 for i in range(10005)]for i in range(5)]
n=int(input())
for i in range(1,4):#f[i][j]表示有i部手机且楼数为j时,最坏运气下的最少测试次数
for j in range(1,n+1):
f[i][j]=j#表示第一部手机从1摔到最后一层都没坏
for i in range(2,4):
for j in range(1,n+1):#f[i-1][k-1]+1表示手机摔坏了,要去楼下去测试,再多试k-1次
for k in range(1,j):#f[i][j-k]+1表示手机没摔坏,手机数量不变,要去楼上再多测试j-k次
f[i][j]=min(f[i][j],max(f[i-1][k-1],f[i][j-k])+1)#min表示最佳策略。max表示最差运气
print(f[3][n])
这个C++可以过,但是python就超时了。过了60%的数据.
五、搜索
搜索是“暴力法”算法思想的具体实现。
BFS—宽度优先搜索
DFS—深度优先搜索

N皇后
x=[0]*15
n=0
sum=0
def pd(k):
for i in range(1,k):
if abs(k-i)==abs(x[k]-x[i]):
return 0
elif x[k]==x[i]:
return 0
return 1
def check(a):
if a>n:
global sum
sum+=1
else:
return False
return True
def DFS(a):
if check(a):
return
else:
for i in range(1,n+1):
x[a]=i
if pd(a):
DFS(a+1)
else:
continue
if __name__=='__main__':
n=int(input())
DFS(1)
print(sum)
路径之谜
写法一:
用这个第一个写法就只能通过5/7的 ,c++转python容易超市
import os
import sys
sys.setrecursionlimit(60000) #调整默认的递归层数,python中常用,默认一般为1000左右
n = 0
flag = [[0 for i in range(26)] for i in range(27)]
resX = [0 for i in range(1000)]
resY = [0 for i in range(1000)]
resCount = 0
# ---------图的路径搜索常用方向移动表示-------
dx = [0, 1, -1, 0]
dy = [1, 0, 0, -1]
# dx[0]=0 dy[0]=1 那么代表向下的方向
# dx[1]=1 dy[1]=0 那么代表向右的方向
# dx[2]=-1 dy[0]=0 那么代表向左的方向
# dx[3]=0 dy[1]=-1 那么代表向上的方向
# --------------------------------------------
def check(x, y):
global n
if x == n & y == n:#如果走到了终点,判断是否所有的箭拔了
for i in range(1, n + 1):
if (col[i] != 0):
return False# 如果箭靶上的数目不为0,根据逆推,我们通过当前路径得不到箭靶上的结果
for i in range(1, n + 1):
if (rol[i] != 0):
return False
for i in range(0, resCount):#打印记录路径
x2 = resX[i]# x 轴坐标
y2 = resY[i]# y 轴坐标
sum = n * (x2 - 1) + y2 - 1# 转换为题目要求的坐标系
print(sum, end=" ")
return False # 成功终止
else:
return True # 继续搜索
# 关于终止还是继续我们交给判定即可
def pd(x2, y2):
global n
if flag[x2][y2] == 1:
return False# 已被走过,不能再走,超出边界
elif x2 < 1:
return False# 从左侧走出方格
elif x2 > n:
return False# 从右侧走出方格
elif col[x2] <= 0:
return False# 没走到右下角,箭用完了
elif y2 < 1:
return False# 从上侧走出方格
elif y2 > n:
return False# 从下侧走出方格
elif rol[y2] <= 0:
return False# 没走到右下角,箭用完了
else:
return True# 符合边界条件,可以继续执行搜索
def dfs(x, y):
if not check(x, y):
return # 包含不符合规则的地方,回溯,用于剪枝
else:
for i in range(0, 4):
xt = dx[i] + x
yt = dy[i] + y
if not pd(xt, yt):
continue# 不符合要求继续换方向搜索
else:
# 因为要进行位置转移,我们给它起个名字,叫作案现场
# 比如向下移动
col[xt] -= 1
rol[yt] -= 1
flag[xt][yt] = 1
global resCount
resX[resCount] = xt
resY[resCount] = yt
resCount += 1
dfs(xt, yt)# 搜索回溯后,因为没有找到正确答案,所以要回复作案现场,返回到搜索之前
resCount -= 1
flag[xt][yt] = 0
col[xt] += 1
rol[yt] += 1
if __name__ == '__main__':
n = int(input())
rol = input().split()
rol = list(map(int, rol))
rol = [0] + rol
col = input().split()
col = list(map(int, col))
col = [0] + col#记录行和列,然后用[0]+X的方式,记录第一个
flag[1][1] = 1
col[1] -= 1
rol[1] -= 1
resX[resCount] = 1
resY[resCount] = 1
resCount += 1
dfs(1, 1)
写法二:
这个写法就是每次优先往剩余箭数多的那一个方向走。实现了优化。
import sys
N=int(input())
X=[int(i) for i in input().split()]
Y=[int(i) for i in input().split()]
steps=sum(X)
path=[]
max_half_steps=max(sum(X[:N//2]),sum(X[N//2:]),sum(Y[:N//2]),sum(Y[N//2:]))#根据行走的步数最多的半边来选择方向
if sum(X[:N//2])==max_half_steps:
directions=[[0,1],[0,-1],[1,0],[-1,0]]
elif sum(X[N//2:])==max_half_steps:
directions=[[1,0],[0,1],[0,-1],[-1,0]]
elif sum(Y[:N//2])==max_half_steps:
directions=[[1,0],[-1,0],[0,1],[0,-1]]
else:
directions=[[0,1],[1,0],[-1,0],[0,-1]]
record=[[0]*N for _ in range(N)]
def dfs(path,position,count):
path.append(position)
x,y=position
record[x][y]=1
X[x]-=1
Y[y]-=1
if count==steps or (x==N-1 and y==N-1):
if count==steps and x==N-1 and y==N-1:
print(' '.join([str(j*N+i) for i,j in path]))
sys.exit()
return
for _x,_y in directions:
if x+_x>=N or y+_y>=N or x+_x<0 or y+_y<0 or X[x+_x]==0 or Y[y+_y]==0 or record[x+_x][y+_y]==1:
continue
dfs(path,[x+_x,y+_y],count+1)
del(path[-1])
X[x+_x]+=1
Y[y+_y]+=1
record[x+_x][y+_y]=0
dfs(path,[0,0],1)
长草
dx = [0, 1, -1, 0]
dy = [1, 0, 0, -1]
# dx[0]=0 dy[0]=1 那么代表向下的方向
# dx[1]=1 dy[1]=0 那么代表向右的方向
# dx[2]=-1 dy[0]=0 那么代表向左的方向
# dx[3]=0 dy[1]=-1 那么代表向上的方向
Map = []
q = []
qfront = 0
qend = 0
n = 0
m = 0
k = 0
length = 0
def pd(x, y):
if x < 0:
return False# x 轴坐标左侧越界
elif x >= n:
return False# x 轴坐标右侧越界
elif y < 0:
return False# y轴坐标上侧越界
elif y >= m:
return False# y 轴坐标下侧越界
elif Map[x][y] == 'g':
return False# 已经长草了
else:
return True# 在范围内,且没长草
def BFS():
global k, q, n, m, Map, length, qend, qfront
while k > 0 and length > 0:
tempPair = q[qfront]
qfront += 1
x = tempPair[0] # 横坐标
y = tempPair[1] # 纵坐标
for i in range(4):
nowx = x + dx[i] # 扩展后的横坐标
nowy = y + dy[i] # 扩展后的纵坐标
if (pd(nowx, nowy)):
q.append((nowx, nowy))
qend += 1
Map[nowx][nowy] = 'g'
length -= 1
if length == 0:#说明上一层的元素已经提取出来了
k -= 1
length = qend - qfront
if __name__ == '__main__':
n, m = map(int, input().split())
Map = [[0 for _ in range(m)] for _ in range(n)] # Python 动态开数组会减少运行时间
for i in range(n):
input_ = input()
for j in range(m):
Map[i][j] = input_[j]
if Map[i][j] == 'g':
q.append((i, j))
qend += 1
k = int(input())
length = qend - qfront
BFS()
for i in range(n):
str_temp = ''
for j in range(m):
str_temp += Map[i][j]
print(str_temp)
走迷宫
dx = [0, 1, -1, 0]
dy = [1, 0, 0, -1]
G = []
Vis = []
# --------队列模拟-----------
q = [] # |
# |
qfront = 0 # |
# |
qend = 0 # |
# --------队列模拟-----------
n = 0
m = 0
ans = 0
startX=0
startY=0
endX=0
endY=0
def pd(x, y):
if x < 1:
return False
# x 轴坐标左侧越界
elif x > n:
return False
# x 轴坐标右侧越界
elif y < 1:
return False
# y轴坐标上侧越界
elif y > m:
return False
# y 轴坐标下侧越界
elif Vis[x][y]!=0:
return False
#已经访问了
elif G[x][y] != '1':
return False
# 已经访问了
else:
return True
def check( x, y):
global ans
if x == endX and y == endY : #找到终点,把距离给他
ans=Vis[x][y];
return True;
else:
return False;
def BFS():
global qend ,qfront
q.append((startX,startY))
qend+=1
Vis[startX][startY]=1
while qend-qfront!=0:
tempPair = q[qfront]
qfront+=1
x = tempPair[0] # 横坐标
y = tempPair[1] # 纵坐标
if check(x,y):
return
for i in range(4):
nowx = x + dx[i] # 扩展后的横坐标
nowy = y + dy[i] # 扩展后的纵坐标
if (pd(nowx, nowy)):
q.append((nowx,nowy))
qend+=1
Vis[nowx][nowy] = Vis[x][y] + 1
if __name__ == '__main__':
n, m = map(int, input().split())
G = [[0 for _ in range(m+10)] for _ in range(n+10)] # Python 动态开数组会减少运行时间
Vis = [[0 for _ in range(m+10)] for _ in range(n+10)] # Python 动态开数组会减少运行时间
for i in range(n):
input_ = input().split()
for j in range(m):
G[i+1][j+1] = input_[j]
startX ,startY , endX ,endY = map(int, input().split())
BFS()
print(ans-1)