【王道计算机组成原理】第二章 数据的表示和运算
第二章 数据的表示和运算
- 2.1 数制与编码
-
- 2.1.1 进位计数制
-
- r进制
- 任意进制->十进制
- 二进制<->八进制、十六进制
- 十进制->任意进制
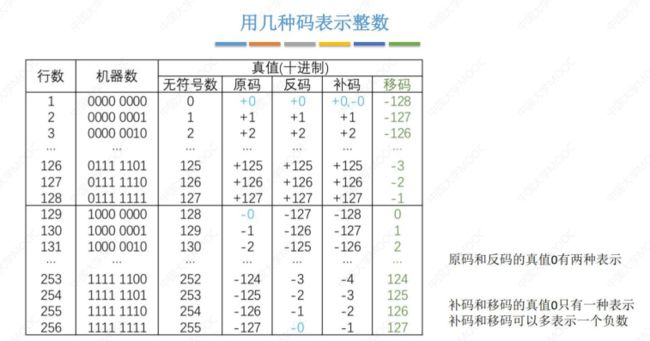
- 真值和机器数
- 2.1.2 BCD码 *
- 2.1.3 定点数的编码表示
-
- 无符号整数的表示和运算
- 带符号整数的表示和运算
-
- 原码表示
- 补码表示
- 移码表示
- 原/反/补/移码特性对比
- 定点小数的表示和运算
- 2.2 运算方法和运算电路
-
- 2.2.0 奇偶校验码*
- 2.2.1 ALU算术逻辑单元
- 2.2.2 并行进位加法器
- 2.2.3 补码加减运算器
- 2.2.4 标志位生产
- 2.2.5 移位运算
-
- 算数移位
- 逻辑移位
- 循环移位
- 2.2.6 定点数运算
-
- 乘法运算
-
- · 原码的一位乘法
- · 补码的一位乘法
- 除法运算
-
- · 原码除法:恢复余数法
- · 补码除法:加减交替法
- 2.2.7 C语言类型转换
- 2.2.8 数据的存储和排列
- 2.3 浮点数的表示与运算
-
- 2.3.1 浮点数的表示
- 2.3.2 IEEE754
- 2.3.3 浮点数的运算
-
- 浮点数的加减运算
- 强制类型转换
2.1 数制与编码
2.1.1 进位计数制
各种进制的常见书写方式:
r进制
- 十进制
- 推广:r 进制计数法
任意进制->十进制
二进制<->八进制、十六进制
十进制->任意进制
eg:75.3
整数部分 = 75:
小数部分 = 0.3:
- 十进制->二进制(拼凑法)
十进制:260.75 -> 1 ¦ 0 0 0 0 ¦ 0 1 0 0 . 1 1
整数部分:260 = 256 + 4 = 2 8 + 2 2
小数部分:0.75 = 0.5 + 0.25 = 2 -1 + 2 -2
十进制:533.125 -> 1 0 ¦ 0 0 0 1 ¦ 0 1 0 1 . 0 0 1
整数部分:533 = 512 + 16 + 4 + 1 = 2 9 + 2 4 + 2 2 + 2 0
小数部分:0.125 = 2 -3
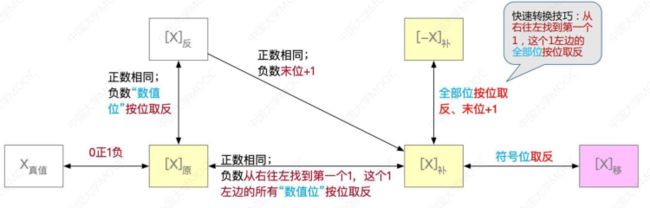
真值和机器数
![]()
2.1.2 BCD码 *
(考纲已删)
如 985 的 8421 码为:1001 1000 0101
其他BCD码
2.1.3 定点数的编码表示
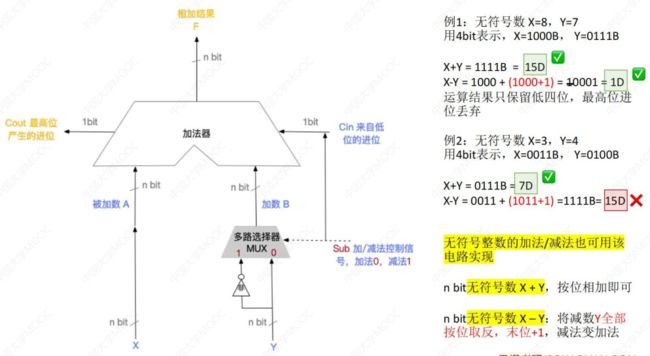
无符号整数的表示和运算
- 无符号整数在计算机硬件内如何表示
计算机硬件能支持的无符号位数是有上限的,是由机器字长限制的:
无符号整数的表示:
- 加法、减法运算的实现原理
✨ 加法:
✨ 减法:
减数B进行变形:
减法变加法:
带符号整数的表示和运算
原码表示
原码缺点:
补码表示
- 原码->反码->补码的转换
- 补码的加法运算
例1:
例2:
- 补码的减法运算
对比无符号整数的减法运算
例3:
移码表示
- 原、反、补、移码的转换
- 移码
原/反/补/移码特性对比
练习:
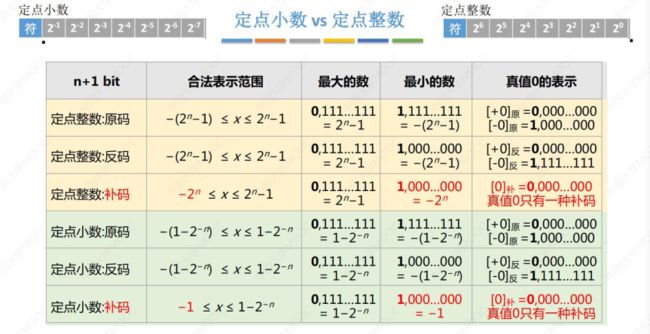
定点小数的表示和运算
- 定点整数、定点小数
- 原码
- 定点小数原、反、补码的转换
- 定点小数的加/减运算
- 定点小数VS定点整数
补码不同于原码、反码,补码的0只有一种表示形式,所以多出来的那位我们人为使它用以表示-1。
例1:
整数补码的加法运算:
小数补码的加法运算:
例2:
整数补码的加法运算:
小数补码的加法运算:
例3:
整数补码的减法运算:
小数补码的加法运算:
2.2 运算方法和运算电路
2.2.0 奇偶校验码*
(大纲已删)
奇偶校验码
例:
重点体会 异或运算
2.2.1 ALU算术逻辑单元
(电路基本原理&加法器设计)
- ALU
- 最基本的逻辑运算
- 复合逻辑
同或:
- 用门电路求偶校验位
- 一位全加器(实现加法运算)
- 串行加法器
- 并行加法器
运算速度很大程度上取决于进位速度
2.2.2 并行进位加法器
- 怎样更快的产生进位?
为了方便观看,记 Gi、Pi :
一般以4个FA作为1个加法器
本小节不是重点,慢慢理解
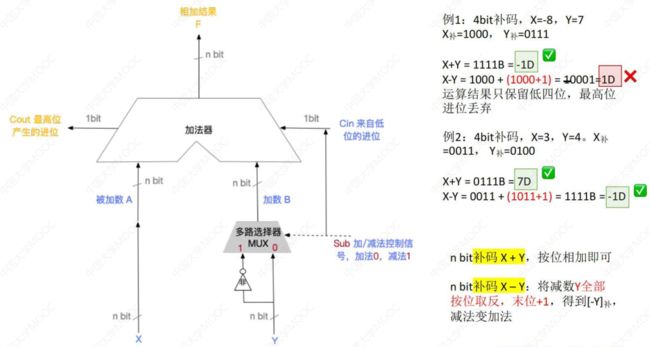
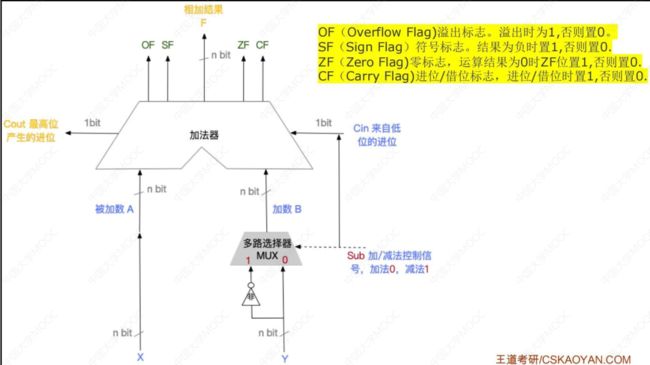
2.2.3 补码加减运算器
- 加法器原理
- 回顾:补码加/减法运算方法
- 实现补码加减运算:
有符号数:
无符号数同:
底层硬件计算逻辑相同,但是 有符号数 和 无符号数 判断溢出的方式不同
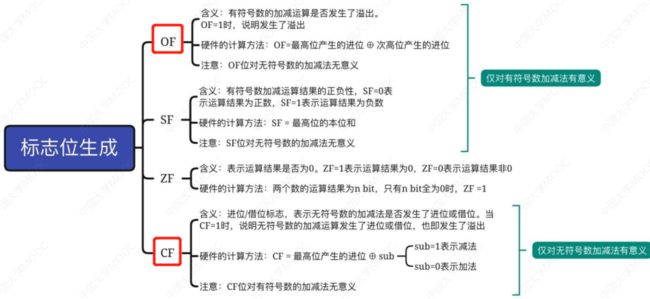
2.2.4 标志位生产
(判断溢出的方式)
2.2.5 移位运算
算数移位
对于10进制:
对于2进制:
⚪ 原码
算数右移:
算数左移:
⚪ 反码
⚪ 补码
- 小总结:
- 应用举例:
计算机的乘法是基于 算数移位 和 加法 进行的
逻辑移位
- 应用举例
循环移位
- 应用举例
对于 大端存储(先存高字节再存低字节)和 小端存储(先存低字节再存高字节) 之间进行转换
2.2.6 定点数运算
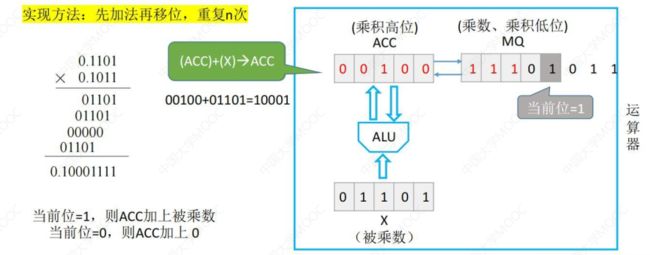
乘法运算
- 实现思想
回忆运算器的基本组成:
· 原码的一位乘法
原码一位乘法:
最低位
下一位的运算同上:
再下一位:
再下一位:
最后的符号位不用参与运算,移位进行了 4 次 (即 n 次)
最后修改符号位:
- 做题手动模拟运算
原码运算时用双符号位或单符号位都可以。但是为了避免和补码运算记混,建议用双符号位。
· 补码的一位乘法
- 补码的一位乘法
辅助位是把MQ扩展了一位来存储
MQ中的最低位指参与乘法运算的最低位(就是不算上 辅助位)
CPU中所有的寄存器长度一般都是统一的,MQ多增加了一位,因此ACC、X也多加一位(多出来的一位可以用来表示 双符号位 的补码)
被乘数采用双符号位的补码,而乘数采用但符号位的补码
- 手算模拟
除法运算
- 实现思想
回忆运算器基本组成:
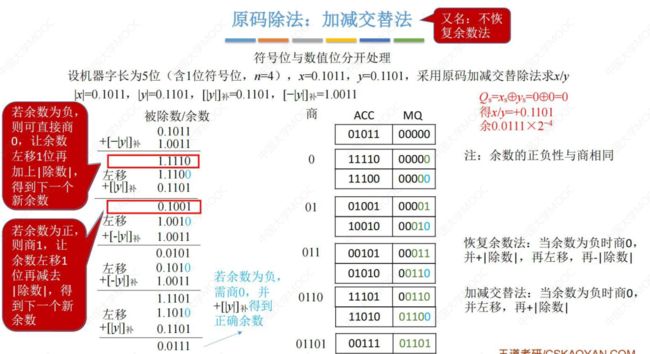
· 原码除法:恢复余数法
默认先上商1:
上商1后计算结果11110送到ACC更新:
ACC检测到符号位为1,即负数,说明应上商0,需要恢复:
ACC、MQ逻辑左移:
确定商的下一位,同上,先上商1:
下一位:
下一位:
下一位:
计算符号位:为0
最终结果:
- 手算模拟:
能否不恢复余数?----> 加减交替法(对恢复余数法的一种优化)
定点小数除法规定 被除数 < 除数,否则结果会大于1,定点小数无法表示大于1的范围。
硬件通过第一步的商来检测:正常情况第一步上商1得到的余数一定要是一个负值(若为正说明被除数 > 除数)
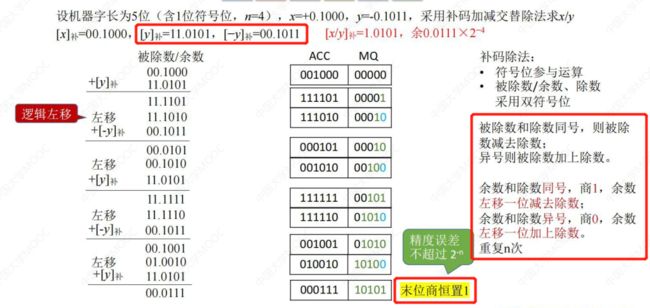
· 补码除法:加减交替法
与原码的加减交替法类似
- 补码加减交替法:
2.2.7 C语言类型转换
2.2.8 数据的存储和排列
- 大小端模式
H:16进制 ; D:10进制 ; B:2进制
- 边界对齐 存储方式
字地址 转 字节地址 :字地址逻辑左移两位(即×4,因为上图中 1字 = 4B)
半字地址 转 字节地址 :半字地址逻辑左移一位
2.3 浮点数的表示与运算
2.3.1 浮点数的表示
- 定点数的局限性
- 从科学计数法理解浮点数
- 浮点数的表示
例:
b的尾数丢失一位,会影响精度,如何优化:
- 浮点数尾数的规格化
仍以上面的 b 为例:
浮点数尾数的规格化:
- 规格化浮点数的特点
负上溢、正上溢已从考试大纲删除
2.3.2 IEEE754
念作 “I triple E”
- 回顾:
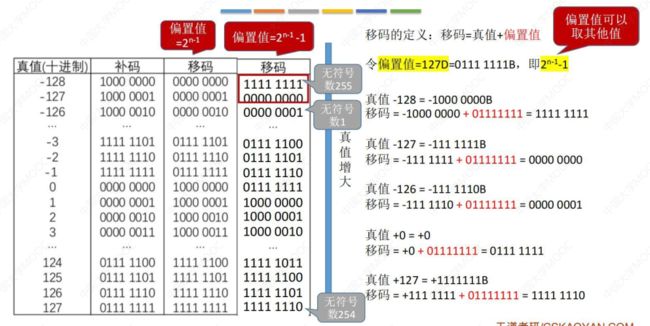
移码偏置值取 2n-1 - 1:
其中:
真值 -128 = - 1000 0000 B
移码 = - 1000 0000 + 0111 1111 偏置值比 -128的绝对值 更小
移码位数只有 8 bit,所有的 ± 运算默认会再进行 mod 28 (即在原有的基础上加上 1 ¦ 0000 ¦ 0000)
故该处:
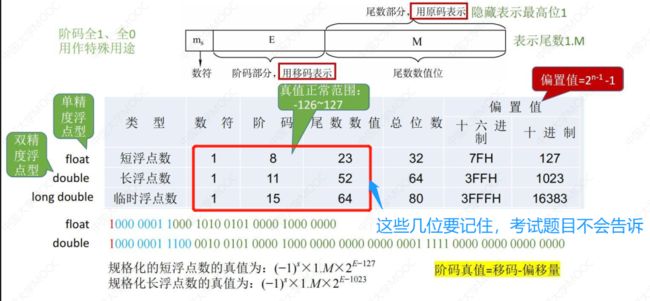
- IEEE754标准
规格化的原码尾数,最高数值位一定是1,因此干脆将其隐藏起来,可以多利用一位。做题时 记得在小数点前加上1,即 1.M才是尾数真正的值
IEEE754中将 阶码全1、全0用作特殊用途,故真值范围为 -126 ~ 127 (原本应为 -128 ~ 127,其中-128为全1、-127为全0,故减去两个数)
上图中 float 偏置值: 2 8 - 1 - 1 = 128 - 1 = 127
double 偏置值: 2 11 - 1 - 1 = 2 10 - 1 - 1 = 1023 即 011¦1111¦1111
计算阶码真值时,可以将移码和偏移量 看作无符号数进行计算
例:
例:
- IEEE754标准单精度浮点型能表示的最小绝对值、最大绝对值
- 若要表示的数绝对值还要更小怎么办?
2.3.3 浮点数的运算
浮点数的加减运算
例:
- 舍入
强制类型转换
考试大多考察32位机器