【数据分析实战】利用python数据清洗后基于机器学习(GBDT和Xgboost算法)对房价预测

导入需要的类库

import pandas as pd    
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
# 忽略警告
warnings.filterwarnings('ignore') 
# 使用 ggplot 画图风格
plt.style.use('ggplot')
%matplotlib inline

导入数据

data = pd.read_csv('train.csv', index_col=0)

该数据是一个维度(1460,80)的数据集。包含了80个特征维度。如果把SalePrice房价作为一个预测值，那么包含了79个特征维度，接下来我们需要对这79个特征维度进行完整的处理，分析。

简单查看数据结构

data.info()

数据有float类型和object类型，我们可以把他们分为两类：数值类型(numerical)数据和类别类型（category）数据。

# 统计数值类型(numerical)特征名，保存为列表
numeric=[f for f in data.drop(['SalePrice'],axis=1).columns 
         if data.drop(['SalePrice'],axis=1).dtypes[f]!='object']
# 统计类别类型（category）特征名，保存为列表
category=[f for f in data.drop(['SalePrice'],axis=1).columns 
          if data.drop(['SalePrice'],axis=1).dtypes[f]=='object']
# 输出数值类型(numerical)特征个数，类型（category）特征个数
print("numeric: {}, category: {}" .format (len(numeric),len(category)))

numeric: 36, category: 43

统计之后发现一共有36+43=79个特征维度。与之前结论吻合。

数据清洗

一份如此庞大的数据集中，可能存在空缺值(NaN)，这些数值会对后续分析产生不利影响，为了满足后续分析的需求，需要在这里对数据进行清洗。

查看数据缺失情况

# 统计每个特征的缺失数
missing = data.isnull().sum()
# 将缺失数从大到小排序
missing.sort_values(inplace=True,ascending=False)
# 选取缺失数大于0的特征
missing = missing[missing > 0]
# 保存含缺失值特征的类型
types = data[missing.index].dtypes
# 计算缺失值百分比
percent = missing / data.shape[0]
# 将缺失值信息整合
missing_data = pd.concat([missing, percent,types],axis=1,
                         keys=['Total', 'Percent','Types'])
# 输出缺失值信息
missing_data

删除缺失数量大于15%的特征维度

如果数据缺失量过大，不管采用什么方式填充，与实际情况的拟合度都会有所偏差，所以对于缺失大于15%的数据统一删除处理。

# 对缺失值超过15%的特征进行删除
data.drop(missing_data[missing_data['Percent'] > 0.15].
          index, axis=1, inplace=True)
# 输出数据维度
print(data.shape)

(1460, 74)

这里删除了6个特征维度，和之前统计的数值吻合。

类别型数据处理

在类别型数据缺失中存在两种情况：
1、本身应该有数据但是缺失。
2、本身就是没有数据，例如建设设施，没有就是没有建设该设施。

情况1用众数填充

data['Electrical'].fillna(data['Electrical'].mode()[0], inplace=True)

情况2用新的类别None代替

cols1 = ['GarageFinish', 'GarageQual', 'GarageType', 'GarageCond', 
         'BsmtFinType2', 'BsmtExposure',
         'BsmtFinType1', 'BsmtQual', 'BsmtCond', 'MasVnrType']
# 依次便利cols1中的特征，对应缺失值用‘None’填充
for col in cols1:
    data[col].fillna('None', inplace=True)

数值类型数据处理

在数据型数据缺失中存在两种情况：
1、本身就是没有数据，例如贴砖面积，本身没有贴砖面积就是空值。
2、本身应该有数据但是缺失。

情况1用0填充

# 由data_description里面的内容的可知，对于数值型数据，如MasVnrArea
#表示砖石贴面面积，如果一个房子本身没有砖石贴面，则缺失值就用0来填补
data['MasVnrArea'].fillna(0, inplace=True)

情况2用None代替

对于 GarageYrBlt车库建造时间，空值表示未建造，可将其离散化，用None填充。但是我们这里希望对年份进行分段处理，对时间特征每20年分一个段，使之呈现出离散状态。

year_map = pd.concat(pd.Series('YearGroup' + str(i+1), 
           index=range(1871+i*20,1891+i*20)) for i in range(0, 7))
data['GarageYrBlt'] = data['GarageYrBlt'].map(year_map)
# 对时间缺失值用‘None’填充
data['GarageYrBlt']= data['GarageYrBlt'].fillna('None')

检查是否还有空缺值

# 常看是否还有空值，最终结果为空即不存在
data.isnull().sum()[data.isnull().sum() > 0]

Series([], dtype: int64)

这里如果用data.isnull().sum()会因为维度过多导致不完全显示，需要调整显示数量，所以，直接用一个Series空集即可。

对SalePrice预测目标进行数据分析

特征维度的数据清洗完成之后，对SalePrice进行一系列数学分析，包括均值，方差，最大最小等值，检查是否正常。

data['SalePrice'].describe()

count 1460.000000
mean 180921.195890
std 79442.502883
min 34900.000000
25% 129975.000000
50% 163000.000000
75% 214000.000000
max 755000.000000

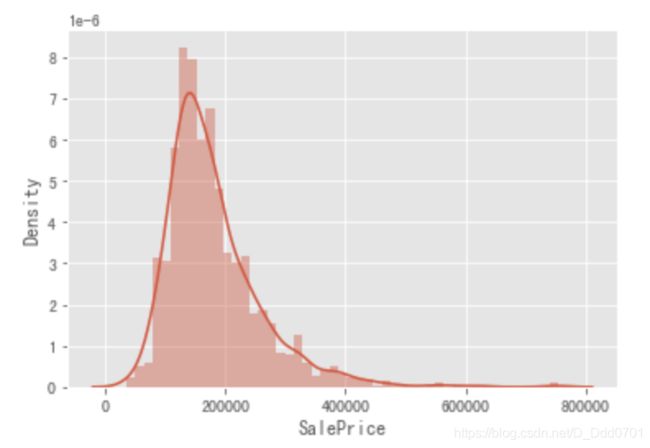
绘制SalePrice概率密度图

sns.distplot(data['SalePrice'],hist=True,kde=True)

偏度峰度计算

我们发现这里的概率密度图并不是呈现标准的正态分布，所以我们需要计算一下偏度和峰度。

# 偏度skewness and 峰度kurtosis计算
# 偏度值离0越远，则越偏
print("Skewness: %f" % data['SalePrice'].skew())
print("Kurtosis: %f" % data['SalePrice'].kurt())

Skewness: 1.882876
Kurtosis: 6.536282

由上面结果可知，偏度大于0.75，则向左偏，采用ln（x+1）进行转化

data['SalePrice'] = np.log1p(data["SalePrice"])
# 画出概率密度图
sns.distplot(data['SalePrice'],hist=True,kde=True)

转化后峰度偏度计算

转化后明显图形更加偏向标准正态分布，再次计算一下峰度和偏度：

print("Skewness: %f" % data['SalePrice'].skew())
print("Kurtosis: %f" % data['SalePrice'].kurt())

Skewness: 0.121347
Kurtosis: 0.809519

删除SalePrice异常值

这里可以采用四分法，在这里就采用一种更简单的方法，我们把基于SalePrice3倍标准差的数值视作异常值，并且删除。

data=data[np.abs(data['SalePrice']-data['SalePrice'].mean())<=(3*data['SalePrice'].std())]

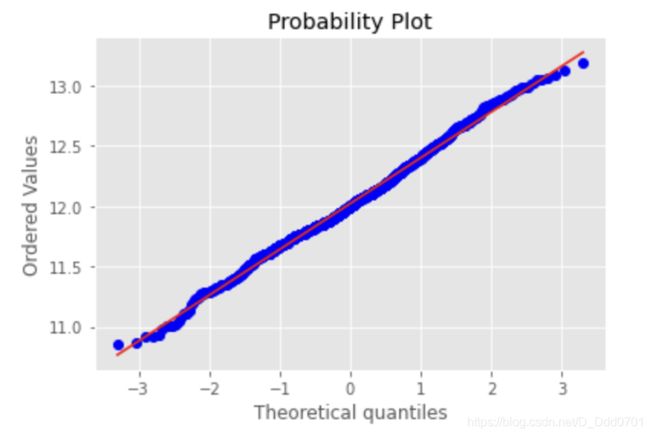
画qq图

qq图斜率表示标准差，截距为均值，查看SalePrice是否服从正态分布，越接近直线，越显正态性。

res = stats.probplot(data['SalePrice'], plot=plt)

此时基本上可以判断这份数据是符合正态分布的。

相关性分析

数值型数据分析

# 计算所有数值型特征与房价的相关系数
corrmat = data.corr()
# 计算与房价相关性大于0.5的特征个数
k = len(corrmat[corrmat['SalePrice'] > 0.5].index)
# 获取前k个重要的特征名
cols = corrmat.nlargest(k,'SalePrice')['SalePrice'].index.tolist()
# 计算该k个特征的相关系数
cm = data[cols].corr()
# 画出可视化热图
plt.figure(figsize=(10,8))
sns.heatmap(cm,annot=True,square=True)

面积特征绘制多变量图

sns.set()
area = ['SalePrice','TotalBsmtSF','1stFlrSF', 'GrLivArea', 'GarageArea']
sns.pairplot(data[area], size = 2.5)

由上图第一行后三个图可知基于’TotalBsmtSF’,‘1stFlrSF’, ‘GrLivArea’,'GarageArea’特征分别存在1、1、2、4个异常值，可剔除掉。

data.drop(data[data['TotalBsmtSF'] > 4000].index, inplace=True)
data.drop(data[data['1stFlrSF'] > 4000].index, inplace=True)
data.drop(data[data['GrLivArea'] > 4000].index, inplace=True)
data.drop(data[data['GarageArea'] > 1240].index, inplace=True)

面积特征峰度偏度计算

print("Skewness: %f" % data['TotalBsmtSF'].skew())
print("Kurtosis: %f" % data['TotalBsmtSF'].kurt())
print("Skewness: %f" % data['1stFlrSF'].skew())
print("Kurtosis: %f" % data['1stFlrSF'].kurt())
print("Skewness: %f" % data['GrLivArea'].skew())
print("Kurtosis: %f" % data['GrLivArea'].kurt())
print("Skewness: %f" % data['GarageArea'].skew())
print("Kurtosis: %f" % data['GarageArea'].kurt())

Skewness: 0.414384
Kurtosis: 1.539572
Skewness: 0.867507
Kurtosis: 1.100841
Skewness: 0.820895
Kurtosis: 0.901041
Skewness: 0.022238
Kurtosis: 0.448625

将偏度大于0.75的’1stFlrSF’, 'GrLivArea’进行ln(x + 1)，转化生成新特征‘ln_1stFlrSF’和‘ln_GrLivArea’。

data['ln_1stFlrSF'] = np.log1p(data["1stFlrSF"])
data['ln_GrLivArea'] = np.log1p(data["GrLivArea"])
print("Skewness: %f" % data['ln_1stFlrSF'].skew())
print("Kurtosis: %f" % data['ln_1stFlrSF'].kurt())
print("Skewness: %f" % data['ln_GrLivArea'].skew())
print("Kurtosis: %f" % data['ln_GrLivArea'].kurt())

Skewness: 0.022909
Kurtosis: -0.200772
Skewness: -0.059680
Kurtosis: -0.241430

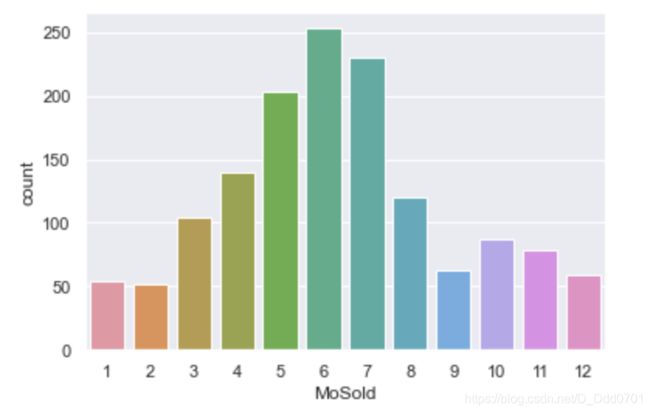
查看非线性特征，不同月份的房子的销售量

sns.countplot(x='MoSold',data=data)

再次统计特征维度数量

numeric = [f for f in data.drop(['SalePrice'], axis=1).columns 
           if data.drop(['SalePrice'], axis=1).dtypes[f] != 'object']
category = [f for f in data.drop(['SalePrice'], axis=1).columns 
            if data.drop(['SalePrice'], axis=1).dtypes[f] == 'object']
# 输出数值类型(numerical)特征个数，类型（category）特征个数
print("numeric: {}, category: {}" .format (len(numeric),len(category)))

numeric: 36, category: 39

对类别类型特征做方差分析

# 定义方差函数，返回p-value值，其值越小对应特征越重要
def anova(frame):
    anv = pd.DataFrame()
    anv['feature'] = category
    pvals = []
    for c in category:
        samples = []
        for cls in frame[c].unique():
            s = frame[frame[c] == cls]['SalePrice'].values
            samples.append(s)
        # stats.f_onewaym模块包用于计算p-value
        pval = stats.f_oneway(*samples)[1]
        pvals.append(pval)
    anv['pval'] = pvals
    # 将特征根据p-valu排序
    return anv.sort_values('pval')

# 将data带入定义的方差函数
a = anova(data)

  feature	pval

7 Neighborhood 2.348768e-237
17 ExterQual 8.553538e-194
29 KitchenQual 2.905300e-184
20 BsmtQual 6.686655e-184
33 GarageFinish 9.518461e-150
32 GarageYrBlt 1.216344e-143
31 GarageType 4.516320e-122
19 Foundation 1.642325e-109
26 HeatingQC 5.024923e-79
23 BsmtFinType1 4.325070e-76
16 MasVnrType 1.706926e-63
14 Exterior1st 1.896956e-58
0 MSZoning 4.750088e-53
15 Exterior2nd 8.502896e-52
34 GarageQual 6.990528e-44
35 GarageCond 1.986807e-43
22 BsmtExposure 3.596751e-43
38 SaleCondition 4.118895e-40
27 CentralAir 1.209771e-36
37 SaleType 1.557651e-35
11 HouseStyle 1.285755e-30
36 PavedDrive 4.658508e-29
28 Electrical 1.035691e-28
21 BsmtCond 1.368291e-28
2 LotShape 7.335546e-28
10 BldgType 1.428896e-13
18 ExterCond 1.043673e-11
24 BsmtFinType2 2.998507e-11
8 Condition1 4.057871e-11
3 LandContour 3.089825e-10
12 RoofStyle 2.513588e-09
25 Heating 8.606465e-08
5 LotConfig 9.219901e-07
30 Functional 9.335996e-07
9 Condition2 3.448231e-03
13 RoofMatl 6.159790e-03
1 Street 9.612655e-02
6 LandSlope 1.406476e-01
4 Utilities 6.144337e-01

重要数据重新整合

数值型和类别型特征维度选出最重要的重新整合：

# 选择相关性大于0.5的重要数值型特征
df = data[cols]
# 将 1stFlrSF 和 GrLivArea 特征ln(x+1)转化
df["1stFlrSF"] = data['ln_1stFlrSF']
df["GrLivArea"] = data['ln_GrLivArea']
# 将时间特征离散化，即没20年分段
df['YearBuilt'] = df['YearBuilt'].map(year_map)
df['YearRemodAdd'] = df['YearRemodAdd'].map(year_map)
# 对非线性特征 MoSold one-hot编码
month = pd.get_dummies(data['MoSold'],prefix='MoSold')
# 合并特征
df = pd.concat([df, month], axis=1)

# 对于类别型数据，跟据方差分析，选取排名重要的25个特征：
features = a['feature'].tolist()[0:25]
# 合并特征
df = pd.concat([df, data[features]], axis=1)

# 查看特征维度
df.shape

(1443, 48)

此时，特征维度已经被降为48个。

特征融合

我们发现，4个面积特征其实可以合并考虑，把4个面积求和得到1个新的特征，实现特征融合。

# 将面积特征相加，构建总面积特征
df["TotalHouse"] = data["TotalBsmtSF"] + data["1stFlrSF"] + data["2ndFlrSF"]
df["TotalArea"] = data["TotalBsmtSF"]+data["1stFlrSF"]+data["2ndFlrSF"]+data["GarageArea"]
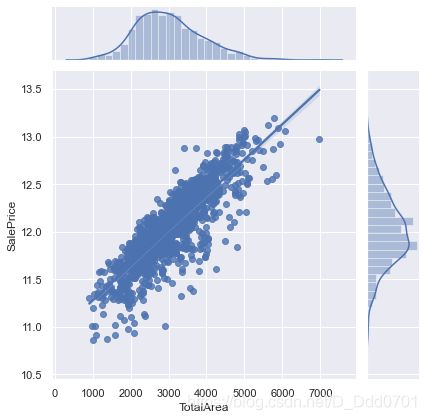
# 画出其回归图
sns.jointplot(x=df["TotalHouse"], y=df['SalePrice'], data = df, kind="reg")
sns.jointplot(x=df["TotalArea"], y=df['SalePrice'], data = df, kind="reg")

由图可知融合的特征较好，TotalHouse、TotalArea分别含有1个异常,可将其剔除掉。

df.drop(df[df['TotalHouse'] > 6000].index, inplace=True)
df.drop(df[df['TotalArea'] > 6500].index, inplace=True)

对其他相关联的特征采用同样的方法融合：

# 继续融合特征
# 将部分相关联的特征进行相加或相乘
df["+_TotalHouse_OverallQual"] = df["TotalHouse"] * data["OverallQual"]
df["+_GrLivArea_OverallQual"] = data["GrLivArea"] * data["OverallQual"]
df["+_BsmtFinSF1_OverallQual"] = data["BsmtFinSF1"] * data["OverallQual"]
df["-_LotArea_OverallQual"] = data["LotArea"] * data["OverallQual"]
df["-_TotalHouse_LotArea"] = df["TotalHouse"] + data["LotArea"]
df["Bsmt"] = data["BsmtFinSF1"] + data["BsmtFinSF2"] + data["BsmtUnfSF"]
df["Rooms"] = data["FullBath"]+data["TotRmsAbvGrd"] 
df["PorchArea"] = data["OpenPorchSF"] + data["EnclosedPorch"] + data["3SsnPorch"] + data["ScreenPorch"]
df["TotalPlace"] = df["TotalBsmtSF"] + data["1stFlrSF"] + data["2ndFlrSF"] + data["GarageArea"] + data["OpenPorchSF"] + data["EnclosedPorch"]+ data["3SsnPorch"] + data["ScreenPorch"]

因为做机器学习的时候无法识别字符串类的信息，我们通常使用虚拟数（dummy）对其转化，例如性别有男、女，我们就用0表示男，1表示女；等级有A、B、C、D，我们就用2表示A，3表示B，4表示C，5表示D。

# 将所有的类别型特征，one-hot编码
df = pd.get_dummies(df)
# 查看数据维度
df.shape

机器学习

导入相关类库

# 构建模型
# 导入GBDT算法
from sklearn.ensemble import GradientBoostingRegressor
# 导入均方误差计算
from sklearn.metrics import mean_squared_error
# 导入标准化模块包
from sklearn.preprocessing import RobustScaler
# 导入划分数据集包，交叉验证包
from sklearn.model_selection import train_test_split,KFold,cross_val_score
# 导入Xgboost算法包
import xgboost as xgb

特征标准化

# 特征标准化
x = RobustScaler().fit_transform(df.drop(['SalePrice'], axis=1).values)
# 提取标签
y = df['SalePrice'].values

5折交叉验证

# 定义验证函数,使用5折交叉验证，采用均方根误差判别，返回均方根误差
def rmse_cv(model):
    # 将数据集shuffle打乱，划分成五分
    kf = KFold(n_splits=5, shuffle=True, random_state=0)
    # 计算均方根误差，其输出结果有五个
    rmse= np.sqrt(-cross_val_score(model,x,y,scoring="neg_mean_squared_error",cv = kf))
    return rmse

5折交叉验证是一种计算均方根误差的方法。它把一堆数据随机分成5份，然后选择其中4个计算均方差。例如数据被分成了ABCDE五组，那么会计算ABCD，ABCE，ABDE，ACDE，BCDE五组分别计算均方差，最后取最好的一个结果当作最终的结果，可以提高模型测试的精度。
当然也可以推广到k折。

GBDT算法

# GBDT算法
# 使用GBDT算法，构建模型
GBoost = GradientBoostingRegressor(n_estimators=3000, learning_rate=0.005,
                                   max_depth=4, max_features='sqrt',
                                   min_samples_leaf=15, min_samples_split=10, 
                                   loss='huber', random_state =5)
score1 = rmse_cv(GBoost)
# 输出五个均方根误差的平均值RSME和其标准差SD,保留4位小数
print("Gradient Boosting score: RSME={:.4f} (SD={:.4f})\n".format(score1.mean(),score1.std()))

Gradient Boosting score: RSME=0.1130 (SD=0.0113)

Xgboost算法

# Xgboost算法,构建模型
Xgboost = xgb.XGBRegressor(colsample_bytree=0.36, gamma=0.042, 
                             learning_rate=0.05, max_depth=3, 
                             min_child_weight=1.88, n_estimators=2200,
                             reg_alpha=0.4640, reg_lambda=0.8571,
                             subsample=0.5213, silent=1,
                             random_state = 1, nthread = -1)
score2 = rmse_cv(Xgboost)
# 输出五个均方根误差的平均值RSME和其标准差SD,保留4位小数
print("Xgboost score: RSME={:.4f} (SD={:.4f})\n".format(score2.mean(),score2.std()))

Xgboost score: RSME=0.1173 (SD=0.0115)

创建训练集和测试集

# 将80%数据作为训练集，20%数据作为测试集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=0)
# 定义回归拟合图,以预测值输入
def drawing(y_hat):
    # 获取预测的测试集从小到大排序的索引
    order = np.argsort(y_hat)
    # 将测试集和预测的测试集按索引排序
    y_test_new = y_test[order]
    y_hat = y_hat[order]
    # 画图展示
    plt.figure(figsize=(8, 6),facecolor='w')
    t = np.arange(len(y_test))
    plt.plot(t, y_test_new, 'b-', linewidth=2, label='True')
    plt.plot(t, y_hat, 'r-', linewidth=2, label='Predicted')
    plt.legend(loc='upper left')
    plt.grid(b=True)
    plt.show()

学习结果

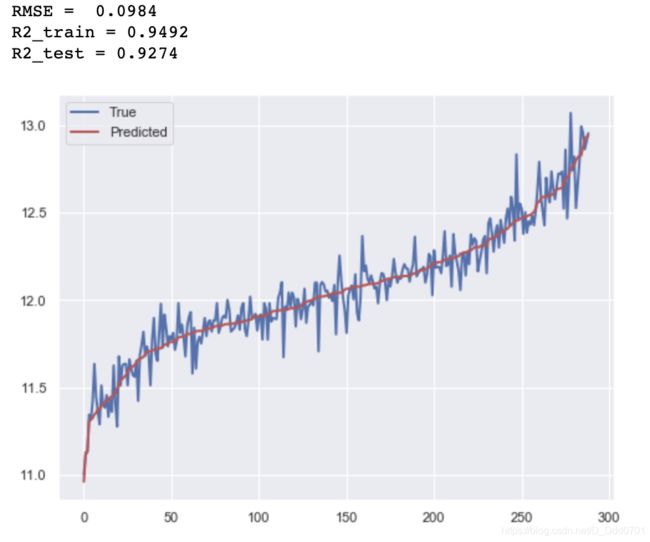
GBDT算法

# 使用GBDT算法，构建模型
# 训练集训练
GBoost.fit(x_train, y_train)
# 测试集结果预测
y_hat1 = GBoost.predict(x_test)
# 分别输出均方根误差RMSE，训练集和测试集的拟合优度R2
print("RMSE =  %.4f" % np.sqrt(np.mean((y_hat1 - y_test) ** 2)))
print('R2_train = %.4f' % GBoost.score(x_train, y_train))
print('R2_test = %.4f' % GBoost.score(x_test, y_test))
# 画出拟合效果图，蓝色表示真实值，红色为预测值
drawing(y_hat1)

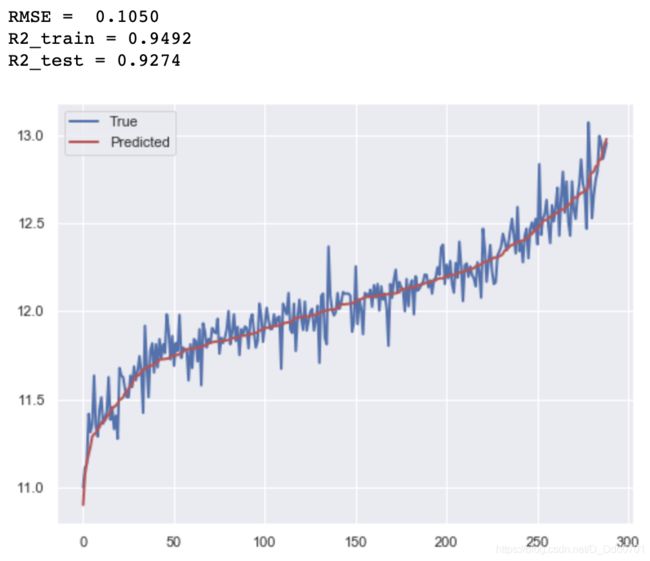
Xgboost算法

# 使用Xgboost算法，构建模型
# 训练集训练
Xgboost.fit(x_train, y_train)
# 测试集结果预测
y_hat2 = Xgboost.predict(x_test)
# 分别输出均方根误差RMSE，训练集和测试集的拟合优度R2
print("RMSE =  %.4f" % np.sqrt(np.mean((y_hat2 - y_test) ** 2)))
print('R2_train = %.4f' % GBoost.score(x_train, y_train))
print('R2_test = %.4f' % GBoost.score(x_test, y_test))
# 画出拟合效果图 ，蓝色表示真实值，红色为预测值
drawing(y_hat2)