优先级队列(堆)的实现,topK问题,堆排序
目录
堆的概念
堆的创建
堆的插入
堆的删除
TopK问题
堆排序
堆的概念
堆是把所有元素按照完全二叉树的顺序存储方式存储到一个一维数组中,根节点最大的为大根堆,根节点最小的为小根堆
这是一个大根堆,要求堆顶元素10比7和5都大.而对7和5之间谁大谁小不作要求
这是一个小根堆,要求堆顶元素3比5和8都小,而对5和8之间谁大谁小不作要求
堆的创建
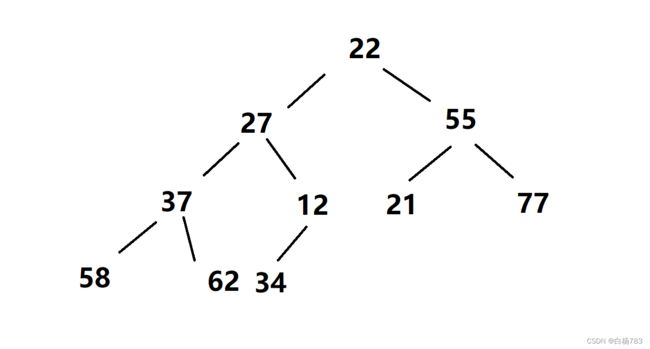
假设现在有集合{22,27,55,37,12,21,77,58,62,34} ,怎样把这个集合中的数据创建为堆呢?
此处我们以创建大根堆为例,如何把上图调整成一个大根堆?
调整过程
1.父亲节点12为根(下标为4),向下调整
2.以37(下标为3),向下调整
3.以55为根(下标为2),向下调整
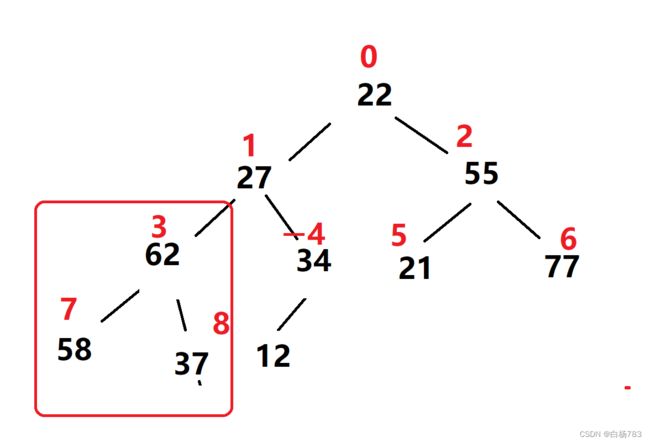
4.27为根(下标为1),向下调整
62比27大,先交换
58比27大,再进行交换
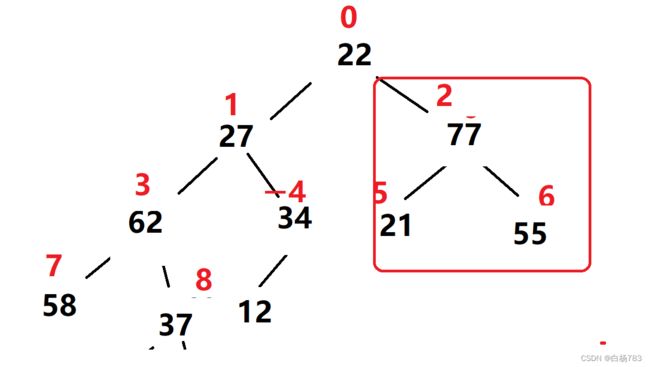
5.最后以22为根(下标为0),向下调整
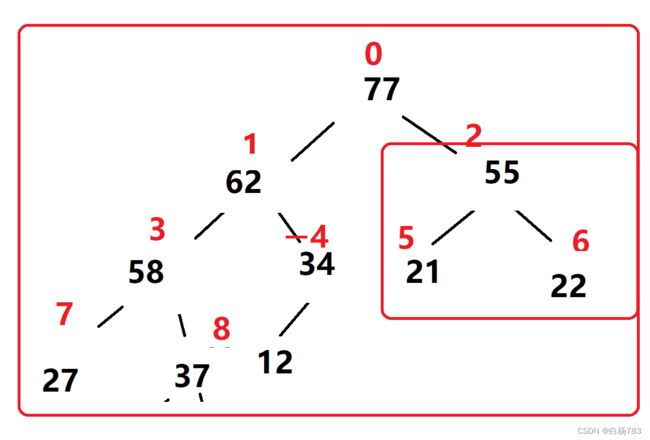
大公告成,此时我们就得到了一个大根堆啦
首先我们采取的是向下调整,找到最后一个父亲节点,此处为12,然后以它为根把它调整成一个大根堆.再调整它前面的一个父亲节点37,把它调整成一个大根堆,依次类推....我们就可以把整颗树调整成一个大根堆
如何找到这个"最后一个父亲节点的下标呢?",我们知道总共有useSize(10)个元素,最后一个元素的下标为child = useSize-1,已知孩子节点求父亲节点:parent = (child-1)/2
拿到父亲节点的下标我们该如何调整这个以父亲节点为根的堆呢?
首先我们得比较它的左孩子和右孩子的最大值与根节点的大小,如果比它大,就交换.因为发生了交换,所有我们不知道它的孩子是否还是一个大根堆,所以还需要调整被交换的孩子为根的堆,此时新的parent = child,新的chid = 2parent+1.什么时候结束呢?当我们得出的孩子的下标大于或等于元素的个数就说明调整完了.
代码实现
public static void main(String[] args) {
int[] array = {22,27,55,37,12,21,77,58,62,34};
createHeap(array);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
System.out.println();
}
public static void createHeap(int[] array){
int child = array.length-1;//最后一个元素的下标
for (int parent = (child-1)/2; parent >=0 ; parent--) {
shiftDown(array,parent,array.length);
}
}
private static void shiftDown(int[] array, int parent, int len) {
int child = 2*parent+1;
while(child < len){
if(child+1 < len && array[child+1]>array[child]){
child++;//此时child一定是左右孩子中最大的
}
//与parent比较大小
if(array[child]>array[parent]){
swap(array,parent,child);//交换
parent = child;
child =2*parent+1;
}else{
break;
}
}
}
private static void swap(int[] array,int x,int y) {
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
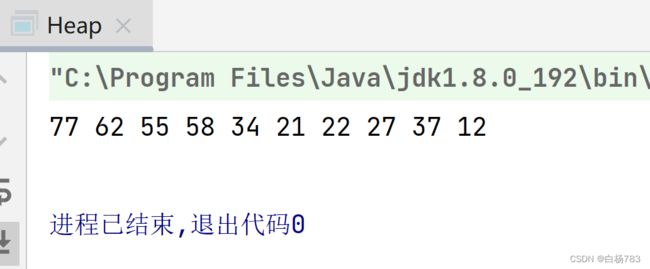
}运行结果
堆的插入
首先我们把要插入的元素放在数组最后,也就是这个堆最后一个节点,此处我们以插入80为例
然后在进行,向上调整,80比34大,交换..这里我们就不需要再管被交换的34了,因为除了被插入的80,其它元素原本都是大根堆,34是父亲节点一定比它的孩子大.
继续向上调整,80比62大,交换,不用管62,它肯定还是一个大根堆
继续向上调整,80比77大交换,大功告成啦!
代码
public static void main(String[] args) {
int[] array = {22,27,55,37,12,21,77,58,62,34};
createHeap(array);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
System.out.println();
//对数组进行扩容
array = Arrays.copyOf(array,array.length+1);
offer(array,80);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
}
public static void offer(int[] array,int val){
array[array.length-1] = val;//把要插入的元素放到最后
int child = array.length-1;
shiftUp(array,child);
}
public static void shiftUp(int[] array ,int child){
int parent = (child-1)/2;
while(child>0){
if(array[parent] < array[child]){
swap(array,parent,child);
child = parent;
parent = (child-1)/2;
}else{
break;
}
}
}结果
堆的删除
堆的删除只能删除对顶元素,简单说下思路,把堆顶元素和最后一个元素交换,再让数组元素个数-1,此是就删除掉了堆顶元素,再对以被交换的元素为根的堆进行向下调整就好了
TopK问题
TopK问题典型的场景是:让你找最大或最小的前k个数据,比如:有10个数据,让你找到前K个最大.最小的数据
很显然最简单的方法是对这10个数据进行排序,然后返回最大/最小的前k个数据.
然而问题是:如果数据量很大,内存装不下怎么办呢?比如假设这里给你10G的数据,让你找出最大或最小的前k个数据.此时如果要是排序的话,我们就需要内存中开辟10G这么大的空间来去存储这么多数据,如果内存没有这么多空间呢?
此时我们就需要使用TopK的思想,比如假设这里要找10G大小的数据中,前K个最大的数据.我们可以使用10G大小的数据中,前K个数据来建立一个小根堆.此时这个小根堆的堆顶元素就是这个堆中最小的元素,拿他和后面的10G-K大小的数据比较,如果堆顶元素比它小,就交换.依次类推,等到全部比较完毕后,此时这个小根堆中所有的元素,就是这10G大小的数据中,前K个最大的数据
这个方法不同在哪呢?我们只需要在内存中开辟一个大小为K的数组来存储数据就可以了,不用把10G大小的数据都放入到内存中
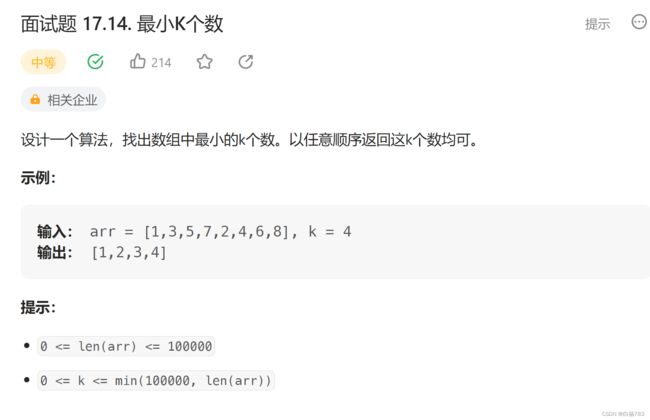
来个例题
力扣
代码
public int[] smallestK(int[] arr, int k) {
if(arr == null || k == 0){
return new int[0];
}
//建立一个大根堆
PriorityQueue maxHeap = new PriorityQueue<>(k,new Comparator(){
@Override
public int compare(Integer o1,Integer o2){
return o2-o1;
}
});
//取出数组中前K个数据放到大根堆中
for(int i = 0;iarr[i]){
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
int[] tmp = new int[k];
for(int i = 0;i 再来一个题:如果让你找出n个数据中,第k小的数据,怎么找?
和刚刚一样,建立一个大小为k的大根堆,遍历剩下的n-k个元素,直接弹出堆顶元素,这就是第k小的值.
因为此时我们堆中存放的是前k个最小的值,而它又是一个大根堆,所以堆顶元素就是第k小的值
堆排序
如果我们要从小到大给一组数据排序,我们应该如何去做呢?
如果我们建立一个小根堆,每次弹出堆顶元素,需要放到一个数组中,这样空间复杂度就大了.(为什么要弹出,因为堆这种结构,本身数据就不是有序的)
所以我们要建立一个大根堆.每次把堆顶元素和最后一个元素交换(下标每次减1)
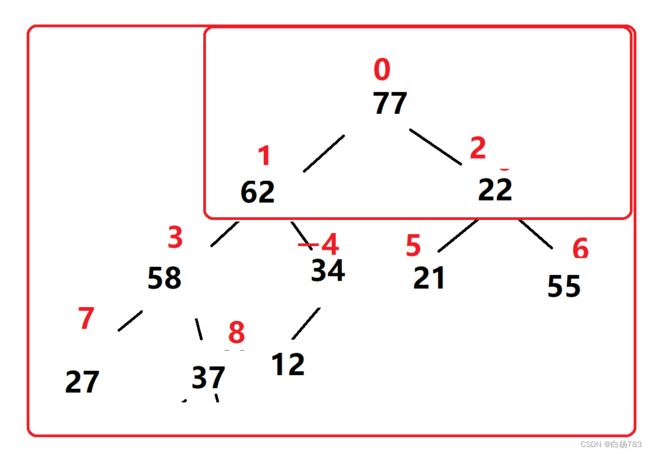
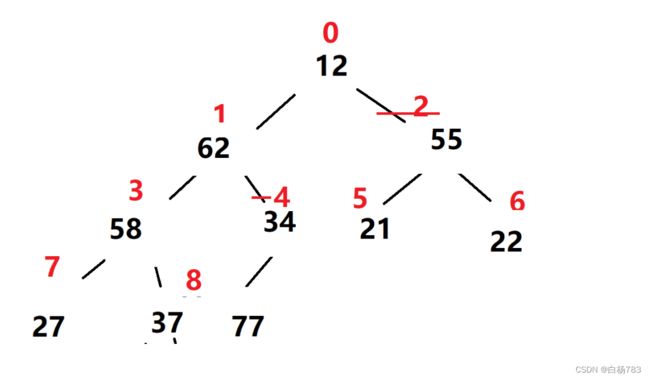
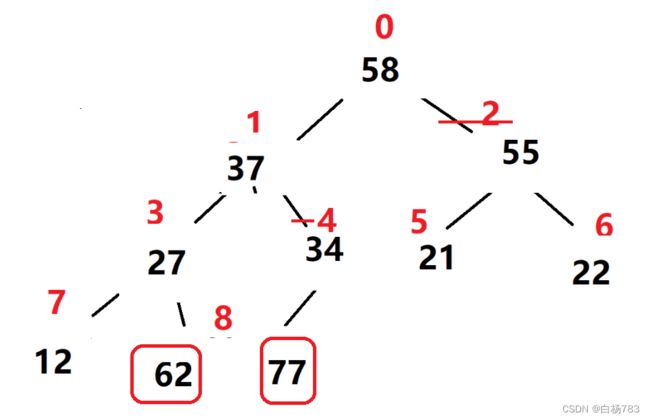
以刚刚这组数据为例,我们先把它建立成一个大根堆
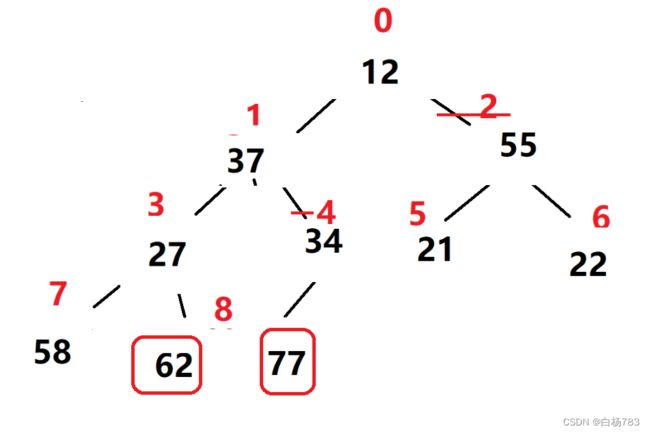
把堆顶元素77和最后一个元素12交换,此时我们的77就是有序的,就不用考虑77了,再重新调整以12为根的这个堆,把它再调整为大根堆.
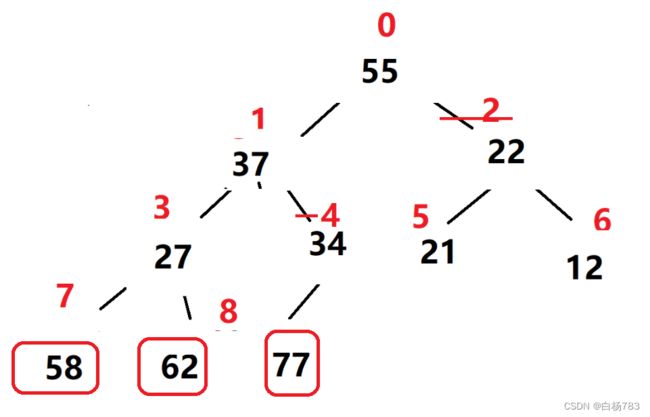
同样,把堆顶元素62和倒数第二个元素62交换,这样62就是有序的,再把剩下的堆向下调整成一个大根堆
同样,把堆顶元素58和倒数第三个元素12进行交换,此时58就是有序的了.再重新把剩下的元素向下调整成一个大根堆
依次类推,最终所有数据都会从小到大,排序完成
代码
public static void main(String[] args) {
int[] array = {22,27,55,37,12,21,77,58,62,34};
heapSort(array);
for (int i = 0; i < array.length; i++) {
System.out.print(array[i]+" ");
}
System.out.println();
}
public static void heapSort(int[] array){
//建立大根堆
createMaxHeap(array);
//堆顶元素和最后一个元素交换
int end = array.length-1;
while (end>0){
swap(array,0,end);
end--;
shiftDown(array,0,end);
}
}
public static void createMaxHeap(int[] array){
int child = array.length-1;//最后一个元素的下标
for (int parent = (child-1)/2; parent >=0 ; parent--) {
shiftDown(array,parent,array.length);
}
}
private static void shiftDown(int[] array, int parent, int len) {
int child = 2*parent+1;
while(child < len){
if(child+1 < len && array[child+1]>array[child]){
child++;//此时child一定是左右孩子中最大的
}
//与parent比较大小
if(array[child]>array[parent]){
swap(array,parent,child);//交换
parent = child;
child =2*parent+1;
}else{
break;
}
}
}
private static void swap(int[] array,int x,int y) {
int tmp = array[x];
array[x] = array[y];
array[y] = tmp;
}运行结果