第十届蓝桥杯大赛软件类决赛(Java 大学A组)
蓝桥杯 2019年国赛真题
Java 大学A组
- 试题 A: 三升序列
- 试题 B: 切割
- 试题 C: 最优旅行
- 试题 D: 骰子制造
- 试题 E: 无方集合
- 试题 F: 大胖子走迷宫
- 试题 G: 估计人数
- 试题 H: 轨道炮
- 试题 I: 矩阵计数
- 试题 J: 分考场
蓝桥杯个人赛软件类历届真题及其解析
试题 A: 三升序列
本题总分: 5 5 5 分
【问题描述】
对于一个字母矩阵,我们称矩阵中的一个三升序列是指在矩阵中找到三个字母,它们在同一行,同一列,或者在同一 45 45 45 度的斜线上,这三个字母从左向右看、或者从上向下看是递增的。
例如,如下矩阵中
YQPD
BKEZ
AFYV
有 B K Z \mathrm{BKZ} BKZ、 B E Z \mathrm{BEZ} BEZ、 A F Y \mathrm{AFY} AFY、 A F V \mathrm{AFV} AFV、 A K P \mathrm{AKP} AKP、 D E F \mathrm{DEF} DEF 等 6 6 6 个三升序列。注意当三个字母是从左下到右上排列时,从左向右看和从上向下看是不同的顺序。
对于下面的 30 30 30 行 50 50 50 列的矩阵,请问总共有多少个三升序列?(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt,内容与下面的文本相同)
VLPWJVVNNZSWFGHSFRBCOIJTPYNEURPIGKQGPSXUGNELGRVZAG
SDLLOVGRTWEYZKKXNKIRWGZWXWRHKXFASATDWZAPZRNHTNNGQF
ZGUGXVQDQAEAHOQEADMWWXFBXECKAVIGPTKTTQFWSWPKRPSMGA
BDGMGYHAOPPRRHKYZCMFZEDELCALTBSWNTAODXYVHQNDASUFRL
YVYWQZUTEPFSFXLTZBMBQETXGXFUEBHGMJKBPNIHMYOELYZIKH
ZYZHSLTCGNANNXTUJGBYKUOJMGOGRDPKEUGVHNZJZHDUNRERBU
XFPTZKTPVQPJEMBHNTUBSMIYEGXNWQSBZMHMDRZZMJPZQTCWLR
ZNXOKBITTPSHEXWHZXFLWEMPZTBVNKNYSHCIQRIKQHFRAYWOPG
MHJKFYYBQSDPOVJICWWGGCOZSBGLSOXOFDAADZYEOBKDDTMQPA
VIDPIGELBYMEVQLASLQRUKMXSEWGHRSFVXOMHSJWWXHIBCGVIF
GWRFRFLHAMYWYZOIQODBIHHRIIMWJWJGYPFAHZZWJKRGOISUJC
EKQKKPNEYCBWOQHTYFHHQZRLFNDOVXTWASSQWXKBIVTKTUIASK
PEKNJFIVBKOZUEPPHIWLUBFUDWPIDRJKAZVJKPBRHCRMGNMFWW
CGZAXHXPDELTACGUWBXWNNZNDQYYCIQRJCULIEBQBLLMJEUSZP
RWHHQMBIJWTQPUFNAESPZHAQARNIDUCRYQAZMNVRVZUJOZUDGS
PFGAYBDEECHUXFUZIKAXYDFWJNSAOPJYWUIEJSCORRBVQHCHMR
JNVIPVEMQSHCCAXMWEFSYIGFPIXNIDXOTXTNBCHSHUZGKXFECL
YZBAIIOTWLREPZISBGJLQDALKZUKEQMKLDIPXJEPENEIPWFDLP
HBQKWJFLSEXVILKYPNSWUZLDCRTAYUUPEITQJEITZRQMMAQNLN
DQDJGOWMBFKAIGWEAJOISPFPLULIWVVALLIIHBGEZLGRHRCKGF
LXYPCVPNUKSWCCGXEYTEBAWRLWDWNHHNNNWQNIIBUCGUJYMRYW
CZDKISKUSBPFHVGSAVJBDMNPSDKFRXVVPLVAQUGVUJEXSZFGFQ
IYIJGISUANRAXTGQLAVFMQTICKQAHLEBGHAVOVVPEXIMLFWIYI
ZIIFSOPCMAWCBPKWZBUQPQLGSNIBFADUUJJHPAIUVVNWNWKDZB
HGTEEIISFGIUEUOWXVTPJDVACYQYFQUCXOXOSSMXLZDQESHXKP
FEBZHJAGIFGXSMRDKGONGELOALLSYDVILRWAPXXBPOOSWZNEAS
VJGMAOFLGYIFLJTEKDNIWHJAABCASFMAKIENSYIZZSLRSUIPCJ
BMQGMPDRCPGWKTPLOTAINXZAAJWCPUJHPOUYWNWHZAKCDMZDSR
RRARTVHZYYCEDXJQNQAINQVDJCZCZLCQWQQIKUYMYMOVMNCBVY
ABTCRRUXVGYLZILFLOFYVWFFBZNFWDZOADRDCLIRFKBFBHMAXX
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
180414
这里程序做的是,枚举三升序列的中间元素,以统计出全部的三升序列,
为了增加代码的重用性,我们使用统计某段连续的元素构成的子序列,从左向右看递增的三升序列程序来统计从上向下看递增的三升序列。
矩阵中的元素可以朝 8 8 8 个方向连续,按行号的增量 x x x 与列号的增量 y y y 构成的二元组 ( x , y ) (x,y) (x,y),分别记为: ( 0 , 1 ) (0,1) (0,1)、 ( − 1 , 1 ) (-1,1) (−1,1)、 ( − 1 , 0 ) (-1,0) (−1,0)、 ( − 1 , − 1 ) (-1,-1) (−1,−1)、 ( 0 , − 1 ) (0,-1) (0,−1)、 ( 1 , − 1 ) (1,-1) (1,−1)、 ( 1 , 0 ) (1,0) (1,0)、 ( 1 , 1 ) (1,1) (1,1)。
其中 ( 0 , 1 ) (0,1) (0,1)、 ( − 1 , 1 ) (-1,1) (−1,1)、 ( 1 , 0 ) (1,0) (1,0)、 ( 1 , 1 ) (1,1) (1,1) 与其余 4 4 4 个方向相逆且均能使用统计 ( 0 , 1 ) (0,1) (0,1) 方向三升序列程序来统计,但我们还能发现 ( − 1 , 1 ) (-1,1) (−1,1) 从上往下看为三升序列时,从左向右恰反,故而再统计一遍其逆方向 ( 1 , − 1 ) (1,-1) (1,−1)。
import java.io.FileInputStream;
public class Test {
static int N = 30, M = 50, K = 5;
int[][] matrix = new int[N][M], offset = {{1, 0}, {0, 1}, {-1, 1}, {1, -1}, {1, 1}};
public static void main(String[] args) { new Test().run(); }
void run() {
try(FileInputStream in = new FileInputStream("inc.txt")) {
int ans = 0, less, more, x, y;
for (int i = 0, bt; i < N; ++i)
for (int j = 0; j < M; ++j) {
do bt = in.read();
while (bt <= 0x20 || bt == 0x7f);
matrix[i][j] = bt;
}
for (int i = 0; i < N; ++i)
for (int j = 0; j < M; ++j)
for (int k = 0; k < K; ++k) {
less = more = 0;
for (x = i, y = j; x >= 0 && y >= 0 && x < N && y < M; x -= offset[k][0], y -= offset[k][1])
if (matrix[x][y] < matrix[i][j]) ++less;
for (x = i, y = j; x >= 0 && y >= 0 && x < N && y < M; x += offset[k][0], y += offset[k][1])
if (matrix[x][y] > matrix[i][j]) ++more;
ans += less * more;
}
System.out.println(ans);
} catch (Exception e) {
e.printStackTrace();
}
}
}
试题 B: 切割
本题总分: 5 5 5 分
【问题描述】
在 4 × 4 4\times4 4×4 的方格矩阵中画一条直线。则直线穿过的方格集合有多少种不同的可能?
这个里直线穿过一个方格当且仅当直线将该方格分割成面积都大于 0 0 0 的两部分。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
267
据说是 267 267 267,但我编的程序计算不出来,先挂着吧。
public class Test {
public static void main(String[] args) { new Test().run(); }
double accuracy = 0.01;
int N = 4, M = 4, ans = 0;
int[][] index = new int[N][M];
boolean[][] zero = new boolean[N + 1][M + 1];
boolean[][] positive = new boolean[N + 1][M + 1];
boolean[] map = new boolean[1 << N * M];
void run() {
for (int i = 0; i < N; ++i)
for (int j = 0; j < M; ++j)
index[i][j] = 1 << i * M + j;
for (double x = 0; x <= N; x += accuracy) {
for (double y = 0; y <= M; y += accuracy) {
total(y / -x, y); // (x1:x, y1:0) (x2:0, y2:y)
total(y / (N - x), -x * y / (N - x)); // (x1:x, y1:0) (x2:N, y2:y)
}
for (double x2 = 0; x2 <= N; x2 += accuracy)
total(M / (x2 - x), -x * M / (x2 - x)); // (x1:x, y1:0) (x2:x2, y2:M)
}
for (double y = 0; y <= M; y += accuracy) {
for (double x = 0; x <= N; x += accuracy)
total((M - y) / x, y); // (x1:0, y1:y) (x2:x, y2:M)
for (double y2 = 0; y2 <= M; y2 += accuracy)
total((y2 - y) / N, y); // (x1:0, y1:y) (x2:N, y2:y2)
}
for (boolean mark : map) if (mark) ++ans;
System.out.println(ans);
}
void total(double k, double b) {
for (int x = 0; x <= N; ++x)
for (int y = 0; y <= M; ++y) {
double tmp = k * x + b - y;
zero[x][y] = abs(tmp) <= 1e-10;
positive[x][y] = tmp > 1e-10;
}
int tot = 0;
for (int x = 0; x < N; ++x)
for (int y = 0; y < M; ++y) {
if (positive[x][y] == positive[x + 1][y] &&
positive[x][y] == positive[x][y + 1] &&
positive[x][y] == positive[x + 1][y + 1]) continue;
if (zero[x][y] && zero[x + 1][y] && zero[x][y + 1] && zero[x + 1][y + 1]) continue;
tot |= index[x][y];
}
map[tot] = true;
}
double abs(double a) { return a > 0 ? a : -a; }
}
试题 C: 最优旅行
本题总分: 10 10 10 分
【问题描述】
中国的高铁四通八达,乘坐方便,小明经常乘坐高铁在城市间旅游。
现在,小明又有了一个长假,他打算继续乘坐高铁旅游。这次,他打算到下面的城市旅游。
上海、广州、长沙、西安、杭州、济南、成都、南京、昆明、郑州、天津、太原、武汉、重庆、南昌、长春、沈阳、贵阳、福州。
小明打算从北京出发,游览以上每个城市正好一次,最终回到北京。在每个城市(除北京外),小明都至少停留 24 24 24 小时。而当小明决定从一个城市去往另一个城市时,他只会选择有直接高铁连接的城市,不会在中途换乘转车。
在试题目录下有一个文件 t r i p . t x t \mathrm{trip.txt} trip.txt 保存了小明可以选择的车次,小明不会选择其他车次。
小明出发的时间是第 1 1 1 天的中午 12 12 12: 00 00 00。请问,小明游览完以上城市正好一次,最终回到北京,最快需要多少分钟(请注意单位为分钟,请注意除北京外的城市需要至少停留 24 24 24 小时,即最少停留 1440 1440 1440 分钟)。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
41613
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.time.LocalTime;
import java.util.*;
public class Test {
public static void main(String[] args) { new Test().run(); }
Map<String, List<Train>> graph = new HashMap();
Map<String, Boolean> visited = new HashMap();
int depth = 0, ans = 0x3f3f3f3f;
void run() {
try(BufferedReader in = new BufferedReader(new InputStreamReader(new FileInputStream("trip.txt"), "GBK"))) {
String line = in.readLine();
while ((line = in.readLine()) != null) {
StringTokenizer token = new StringTokenizer(line);
token.nextToken();
String u = token.nextToken();
String v = token.nextToken();
int start = LocalTime.parse(token.nextToken()).toSecondOfDay() / 60;
int end = LocalTime.parse(token.nextToken()).toSecondOfDay() / 60;
if (!graph.containsKey(u)) {
graph.put(u, new ArrayList());
visited.put(u, false);
}
graph.get(u).add(new Train(v, start, end));
}
dfs("北京", (visited.size() - 1) * 1440 + 720);
System.out.println(ans - 720);
} catch (Exception e) {
e.fillInStackTrace();
}
}
void dfs(String start, int time) {
if (time > ans) return;
if (depth == visited.size() && start.equals("北京")) ans = min(ans, time);
for (Train train : graph.get(start)) {
if (visited.get(train.to)) continue;
visited.put(train.to, true);
++depth;
if (time % 1440 > train.start)
dfs(train.to, time + 1440 - time % 1440 + train.end);
else
dfs(train.to, time - time % 1440 + train.end);
visited.put(train.to, false);
--depth;
}
}
int min(int arg1, int arg2) { return arg1 < arg2 ? arg1 : arg2; }
class Train {
String to;
int start, end;
Train(String to, int start, int end) {
this.to = to;
this.start = start;
this.end = end;
}
}
}
很莫名其妙的一道搜索题,这里没做字符串到整型的映射是因为,你编写完这部分程序,你写的暴力早把结果跑出来了。
想自己跑一遍这个程序的,等上半分钟吧。
试题 D: 骰子制造
本题总分: 10 10 10 分
【问题描述】
骰子是游戏中常用的一个工具,骰子是一个正六面体,六个面分别是 1 1 1 到 6 6 6 点,每种一个,通常情况下, 1 1 1 到 6 6 6 点的样子如下图所示。

其中 1 1 1、 4 4 4、 5 5 5 点旋转 90 90 90、 180 180 180、 270 270 270 度后形状不变,而 2 2 2、 3 3 3、 6 6 6 点旋转 180 180 180 度后形状不变。
小明要制造一批骰子,他希望制造出来后有意思一点,他希望他制造出来的骰子任何两个旋转后都是不相同的。请问,他最多能造出多少个?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
240
伯恩赛德引理
Burnside’s lemma
设 G G G 是一个有限群,作用在集合 X X X 上。对每个 g g g 属于 G G G 令 X g X^g Xg 表示 X X X 中在 g g g 作用下的不动元素。伯恩赛德引理断言轨道数(记作 ∣ X / G ∣ |X/G| ∣X/G∣)由如下公式给出: ∣ X / G ∣ = 1 ∣ G ∣ ∑ g ∈ G ∣ X g ∣ . |X/G|=\frac 1{\left|G\right|}\sum_{g\in G}|X^g|. ∣X/G∣=∣G∣1g∈G∑∣Xg∣. 从而轨道数(是一个自然数或无穷)等于被 G G G 中一个元素保持不动的点个数的平均值(故同样是自然数或无穷)。
—— 摘自 Wiki
更具体地说, X X X 为不考虑旋转后都是否相同的骰子方案集合,显然 ∣ X ∣ = 6 ! × 2 3 |X| = 6!\times2^3 ∣X∣=6!×23, G G G 为骰子上的置换群,容易得知 ∣ G ∣ = 24 |G| = 24 ∣G∣=24(因为阐述 B u r n s i d e ′ s l e m m a \mathrm{Burnside's\ lemma} Burnside′s lemma 的文章中,绝大多数都会以立方体染色为例,经过一系列自然语言描述后,可以得到 ∣ G ∣ = 1 + 6 + 3 + 6 + 8 = 24 |G| = 1 + 6 + 3 + 6 + 8 = 24 ∣G∣=1+6+3+6+8=24), X g X^g Xg 只当 g = e g = e g=e 时不为零,因为骰子六个面都不相同。
所以,最终答案为 1 24 6 ! × 2 3 = 240 \displaystyle{\frac 1{24}6!\times2^3 = 240} 2416!×23=240。
或者可以从组合的方向来思考,设骰子的六个面分别为:顶、底、前、后、左、右,由于某个面必然会出现在骰子上,故我们将 1 1 1 确定到顶而不计入方案数,此时底有 5 5 5 种取法,同样的,我们取某个未取的数作为前,则后有 3 3 3 种取法,左右此时已经确定,但还是有 2 2 2 种排列法,
故,只考虑点数,不考虑花纹,能造出的不相同的骰子至多有 5 × 3 × 2 = 30 5 \times 3 \times 2 = 30 5×3×2=30 个,同时 2 2 2、 3 3 3、 6 6 6 点有两种不同的花纹,故答案为 30 × 2 3 = 240 30 \times 2^3 = 240 30×23=240。
试题 E: 无方集合
本题总分: 15 15 15 分
【问题描述】
小明不是很喜欢完全平方数,他甚至不喜欢加起来是完全平方数的两个数。
今天,他想从 1 1 1 到 100 100 100 中选择一些数组成一个集合,要求不选择任何一个完全平方数,集合中任意两个数相加也不能是完全平方数。请问,小明最多能选出多少个数。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
36
最大独立集
一般图上的最大独立集,容易考虑到 B r o n \mathrm{Bron} Bron– K e r b o s c h \mathrm{Kerbosch} Kerbosch 算法,但朴素的 B K \mathrm{BK} BK 复杂度上界在 O ( 3 n 3 ) O(3^{\frac n3}) O(33n),通常我们难以达到这个上界,
所以我去碰瓷了,莫约跑了 24 24 24 分钟,
N P C \mathrm{NPC} NPC 问题就是恶心,下面给出一种概率性算法,设一般图 G = ( V , E ) G=(V,E) G=(V,E), n = ∣ V ∣ n = |V| n=∣V∣, G G G 的顶点分别为 1 ∼ n 1 \sim n 1∼n,容易在 O ( n 2 ) O(n^2) O(n2) 的复杂度内确定一个 n n n 级排列的元素代表的顶点构成的显然团的大小,跟进一步地说。
设 G G G 的最大团的某个排序为 G ′ = v 1 , v 2 , ⋯ , v m G'=v_1,v_2,\cdots,v_m G′=v1,v2,⋯,vm,我们随机的给出 n n n 级排列 S S S,其中 S S S 存在一个子序列 S ′ = G ′ S' = G' S′=G′(顺序不对就重排 G ′ G' G′), v i v_i vi 在 S S S 中的位置为 w i w_i wi,当 ∀ i \forall i ∀i, s i ∉ G i s_i \not\in G_i si∈Gi,都 ∃ j \exists j ∃j, w j < i ∧ w j ↮ s i w_j wj<i∧wj↔si 时,我们朴素的去确定 S S S 上的显然团,就能确定出 G G G 上的最大团。
细节和“显然团”就看我代码吧,
能力有限就不计算复杂度了。
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Test {
public static void main(String[] args) { new Test().run(); }
int N = 100, times = 100000, ans = 0, m;
boolean[] square = new boolean[2 * N];
List<Integer> G = new ArrayList();
int[] T = new int[N];
void run() {
for (int i = 1; i * i < 2 * N; ++i) square[i * i] = true;
for (int i = 1; i <= N; ++i)
if (!square[i]) G.add(i);
while (times-- > 0) {
Collections.shuffle(G);
m = 0; flag: for (int u : G) {
for (int v = 0; v < m; ++v)
if (square[u + T[v]]) continue flag;;
T[m++] = u;
}
ans = Math.max(ans, m);
}
System.out.println(ans);
}
}
答案不对可以重复运行几次,或调整times增加ans逼近最大团的概率,如是在比赛现场,我会给times再加两个 0 0 0。
试题 F: 大胖子走迷宫
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 15 15 15 分
【问题描述】
小明是个大胖子,或者说是个大大胖子,如果说正常人占用 1 × 1 1 × 1 1×1 的面积,小明要占用 5 × 5 5 × 5 5×5 的面积。
由于小明太胖了,所以他行动起来很不方便。当玩一些游戏时,小明相比小伙伴就吃亏很多。
小明的朋友们制定了一个计划,帮助小明减肥。计划的主要内容是带小明玩一些游戏,让小明在游戏中运动消耗脂肪。走迷宫是计划中的重要环节。
朋友们设计了一个迷宫,迷宫可以看成是一个由 n × n n × n n×n 个方阵组成的方阵,正常人每次占用方阵中 1 × 1 1 × 1 1×1 的区域,而小明要占用 5 × 5 5 × 5 5×5 的区域。小明的位置定义为小明最正中的一个方格。迷宫四周都有障碍物。
为了方便小明,朋友们把迷宫的起点设置在了第 3 3 3 行第 3 3 3 列,终点设置在了第 n − 2 n − 2 n−2 行第 n − 2 n − 2 n−2 列。
小明在时刻 0 0 0 出发,每单位时间可以向当前位置的上、下、左、右移动单位 1 1 1 的距离,也可以停留在原地不动。小明走迷宫走得很辛苦,如果他在迷宫里面待的时间很长,则由于消耗了很多脂肪,他会在时刻 k k k 变成一个胖子,只占用 3 × 3 3 × 3 3×3 的区域。如果待的时间更长,他会在时刻 2 k 2k 2k 变成一个正常人,只占用 1 × 1 1 × 1 1×1 的区域。注意,当小明变瘦时迷宫的起点和终点不变。
请问,小明最少多长时间能走到迷宫的终点。注意,小明走到终点时可能变瘦了也可能没有变瘦。
【输入格式】
输入的第一行包含两个整数 n , k n, k n,k。
接下来 n n n 行,每行一个由 n n n 个字符组成的字符串,字符为 + + + 表示为空地,字符为 ∗ * ∗ 表示为阻碍物。
【输出格式】
输出一个整数,表示答案。
【样例输入】
9 5
+++++++++
+++++++++
+++++++++
+++++++++
+++++++++
***+*****
+++++++++
+++++++++
+++++++++
【样例输出】
16
【评测用例规模与约定】
对于 30 % 30\% 30% 的评测用例, 1 ≤ n ≤ 50 1 ≤ n ≤ 50 1≤n≤50。
对于 60 % 60\% 60% 的评测用例, 1 ≤ n ≤ 100 1 ≤ n ≤ 100 1≤n≤100。
对于所有评测用例, 1 ≤ n ≤ 300 , 1 ≤ k ≤ 1000 1 ≤ n ≤ 300,1 ≤ k ≤ 1000 1≤n≤300,1≤k≤1000。
b f s \mathrm{bfs} bfs,需要一定的枝剪。
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Deque;
public class Main {
public static void main(String[] args) { new Main().run(); }
int[][] offset = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}, {0, 0}, {-1, -1}, {-1, 1}, {1, -1}, {1, 1}};
void run() {
try(BufferedReader in = new BufferedReader(new InputStreamReader(System.in))) {
String line = in.readLine(), temp[] = line.split(" ");
int n = Integer.parseInt(temp[0]);
int k = Integer.parseInt(temp[1]);
boolean[][][] map = new boolean[3][n + 2][n + 2];
boolean[][] visited = new boolean[n + 1][n + 1];
for (int i = 1; i <= n; ++i) {
line = in.readLine();
for (int j = 1; j <= n; ++j)
map[0][i][j] = line.charAt(j - 1) == '+';
}
for (int g = 1; g <= 2; ++g)
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j) {
boolean flag = true;
for (int l = 0; l < 9; ++l)
if (!map[g - 1][i + offset[l][0]][j + offset[l][1]]) {
flag = false;
break;
}
if (flag) map[g][i][j] = true;
}
Deque<Node> queue = new ArrayDeque();
queue.offer(new Node(3, 3, 0));
visited[3][3] = true;
while (!queue.isEmpty()) {
Node now = queue.poll();
if (now.x == n - 2 && now.y == n - 2) {
System.out.println(now.time);
return;
}
int z = 2;
if (now.time >= k) z = 1;
if (now.time >= 2 * k) z = 0;
++now.time;
for (int i = 0, x, y; i < 4; ++i) {
x = now.x + offset[i][0];
y = now.y + offset[i][1];
if (map[z][x][y] && !visited[x][y]) {
queue.offer(new Node(x, y, now.time));
visited[x][y] = true;
}
}
if (z > 0) queue.offer(now);
}
} catch (IOException e) {
e.printStackTrace();
}
}
class Node {
int x, y, time;
Node(int x, int y, int time) {
this.x = x;
this.y = y;
this.time = time;
}
}
}
试题 G: 估计人数
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 20 20 20 分
【问题描述】
给定一个 N × M N\times M N×M 的方格矩阵,矩阵中每个方格标记 0 0 0 或者 1 1 1 代表这个方格是不是有人踩过。
已知一个人可能从任意方格开始,之后每一步只能向右或者向下走一格。走了若干步之后,这个人可以离开矩阵。这个人经过的方格都会被标记为 1 1 1,包括开始和结束的方格。注意开始和结束的方格不需要一定在矩阵边缘。
请你计算至少有多少人在矩阵上走过。
【输入格式】
输入第一行包含两个整数 N 、 M N、M N、M。
以下 N N N 行每行包含 M M M 个整数 ( 0 / 1 ) (0/1) (0/1),代表方格矩阵。
【输出格式】
输出一个整数代表答案。
【样例输入】
5 5
00100
11111
00100
11111
00100
【样例输出】
3
【评测用例规模与约定】
对于所有评测用例, 1 ≤ N , M ≤ 20 1 ≤ N, M ≤ 20 1≤N,M≤20,标记为 1 1 1 的方格不超过 200 200 200 个。
最小路径覆盖
经典的模板,铸就标准的零分。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) { new Main().run(); }
int V, E, match[], visited[];
boolean graph[][];
void run() {
try(BufferedReader in = new BufferedReader(new InputStreamReader(System.in))) {
String line = in.readLine(), temp[] = line.split(" ");
int n = Integer.parseInt(temp[0]);
int m = Integer.parseInt(temp[1]);
int[][] map = new int[n + 1][m + 1];
for (int i = 0; i < n; ++i) {
line = in.readLine();
for (int j = 0; j < m; ++j)
if (line.charAt(j) == '1') map[i][j] = ++V;
}
visited = new int[V + 1];
match = new int[V + 1];
graph = new boolean[V + 1][V + 1];
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
if (map[i][j] > 0) {
if (map[i + 1][j] > 0)
graph[map[i][j]][map[i + 1][j]] = true;
if (map[i][j + 1] > 0)
graph[map[i][j]][map[i][j + 1]] = true;
}
for (int k = 1; k <= V; ++k)
for (int i = 1; i <= V; ++i)
for (int j = 1; j <= V; ++j)
if (graph[i][k] & graph[k][j]) graph[i][j] = true;
for (int i = 1; i <= V; ++i)
if (dfs(i, i)) ++E;
System.out.println(V - E);
} catch (IOException e) {
e.printStackTrace();
}
}
boolean dfs(int x, int flag) {
for (int y = 1; y <= V; ++y)
if (graph[x][y] && visited[y] != flag) {
visited[y] = flag;
if (match[y] == 0 || dfs(match[y], flag)) {
match[y] = x;
return true;
}
}
return false;
}
}
试题 H: 轨道炮
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 20 20 20 分
【问题描述】
小明在玩一款战争游戏。地图上一共有 N N N 个敌方单位,可以看作 2 D 2\mathrm D 2D 平面上的点。其中第 i i i 个单位在 0 0 0 时刻的位置是 ( X i , Y i ) (X_i, Y_i) (Xi,Yi),方向是 D i D_i Di (上下左右之一,用 ’ U ’ / ’ D ’ / ’ L ’ / ’ R ’ ’\mathrm U’/’\mathrm D’/’\mathrm L’/’\mathrm R’ ’U’/’D’/’L’/’R’ 表示),速度是 V i V_i Vi。
小明的武器是轨道炮,只能使用一次,不过杀伤力巨大。小明可以选择在某个非负整数时刻释放轨道炮,轨道炮一次可以消灭在一条直线 (平行于坐标轴) 上的所有敌方单位。
请你计算小明最多能消灭多少敌方单位。
【输入格式】
输入第一行包含一个整数 N N N。
以下 N N N 行每行包含 3 3 3 个整数 X i , Y i , V i X_i, Y_i, V_i Xi,Yi,Vi,以及一个大写字符 D i D_i Di。
【输出格式】
输出一个整数代表答案。
【样例输入】
4
0 0 1 R
0 10 1 R
10 10 2 D
2 3 2 L
【样例输出】
3
【评测用例规模与约定】
对于所有评测用例, 1 ≤ N ≤ 1000 , − 1000000 ≤ X i , Y i ≤ 1000000 , 0 ≤ V i ≤ 1000000 1 ≤ N ≤ 1000,−1000000 ≤ X_i, Y_i ≤ 1000000,0 ≤ V_i ≤ 1000000 1≤N≤1000,−1000000≤Xi,Yi≤1000000,0≤Vi≤1000000。
大模拟,
N ≥ 1 N \geq 1 N≥1,故必然有一个敌方单位会被消灭,所以只用遍历所有敌方单位,求出包含消灭该单位的时间片段里,最大消灭数即可。
蓝桥云课 上该题打着 贪心 标签,没看出来哪能贪。
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.io.IOException;
import java.util.HashMap;
import java.util.Map;
public class Main {
public static void main(String[] args) { new Main().run(); }
void run() {
int n = nextInt(), V;
int[] X = new int[n];
int[] Y = new int[n];
int[] Vx = new int[n];
int[] Vy = new int[n];
for (int i = 0; i < n; ++i) {
X[i] = nextInt();
Y[i] = nextInt();
V = nextInt();
switch (nextChar()) {
case 'U': Vy[i] = V; break;
case 'D': Vy[i] = -V; break;
case 'L': Vx[i] = -V; break;
case 'R': Vx[i] = V; break;
}
}
System.out.println(max(calc(X, Vx, n), calc(Y, Vy, n)));
}
int calc(int[] X, int[] V, int n) {
int res = 0;
for (int i = 0; i < n; ++i) {
Map<Integer, Integer> map = new HashMap();
int max = 0, cnt = 1;
for (int j = i + 1; j < n; ++j) {
if (V[i] == V[j]) {
if (X[i] == X[j]) ++cnt;
} else {
int x = X[i] - X[j];
int v = V[j] - V[i];
int t = x / v;
if (t < 0 || x % v != 0) continue;
Integer up = map.get(t);
up = up != null ? up + 1 : 1;
max = max(max, up);
map.put(t, up);
}
}
res = max(res, max + cnt);
}
return res;
}
int max(int arg1, int arg2) { return arg1 > arg2 ? arg1 : arg2; }
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
StreamTokenizer nextToken(StreamTokenizer in) {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return in;
}
int nextInt() { return (int)nextToken(in).nval; }
char nextChar() { return nextToken(in).sval.charAt(0); }
}
试题 I: 矩阵计数
时间限制: 1.0 s 1.0\mathrm s 1.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 25 25 25 分
【问题描述】
一个 N × M N\times M N×M 的方格矩阵,每一个方格中包含一个字符 O O O 或者字符 X X X。
要求矩阵中不存在连续一行 3 3 3 个 X X X 或者连续一列 3 3 3 个 X X X。
问这样的矩阵一共有多少种?
【输入格式】
输入一行包含两个整数 N N N 和 M M M。
【输出格式】
输出一个整数代表答案。
【样例输入】
2 3
【样例输出】
49
【评测用例规模与约定】
对于所有评测用例, 1 ≤ N , M ≤ 5 1 ≤ N, M ≤ 5 1≤N,M≤5。
状压 dp
在一个 N × M N\times M N×M 、每个方格都填上了字符 O O O 的方格矩阵上,自顶向下地将 O O O 替换为 X X X,可以预见的是,当前的摆放方案某个方格由 O O O 变 X X X 是否合法,取决于当前列上两格,以及当前行的 X X X 分布,容易想到将 X X X 的摆放方案以行为单位组织,具体地说。
设有一个长度为 M M M 的 3 3 3 进制串 f i f_i fi,串中第 j j j 位表示至 i i i 行 j j j 列以及该单元格向上数共连续地摆有多少个 X X X,由于我们是按行组织,故而转移也是考虑按行进行,状态 f i f_i fi 能摆放在 g i − 1 g_{i-1} gi−1 下,需满足 f i f_i fi 每一个数位上的数字不能大于 1 1 1( f i f_i fi 只表示单行),且不存在连续的三个数位上都非是非零数字(行合法), f i + g i − 1 f_i + g_{i-1} fi+gi−1 不存在某一数位上的数字大于等于 3 3 3(列合法),则能转移到新的状态 f i ′ f_i' fi′, f i ′ f_i' fi′ 的第 k k k 位 f i ′ [ k ] = { 0 f i [ k ] = 0 f i [ k ] + g i − 1 [ k ] o t h e r w i s e f_i'[k] = \begin{cases}0& f_i[k] = 0\\f_i[k]+g_{i-1}[k] &otherwise\end{cases} fi′[k]={0fi[k]+gi−1[k]fi[k]=0otherwise.
状压 d p \mathrm{dp} dp 就那样,蓝桥也玩不出花来。
import java.util.Scanner;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Main {
public static void main(String[] args) { new Main().run(); }
int ans, N, M = 1, K = 3;
void run() {
Scanner in = new Scanner(System.in);
int n = in.nextInt(), m = in.nextInt();
for (; m > 0; --m) M *= 3;
List<Integer>[] linked = new List[M];
int[] checked = new int[M];
int[] mapping = new int[M];
for (int i = 0; i < M; ++i)
if (check(i, 3)) {
mapping[i] = N;
checked[N] = i;
linked[N++] = new ArrayList();
}
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
if (check(checked[i], 2)){
int buf = leftAdd(checked[i], checked[j]);
if (buf >= 0) linked[mapping[buf]].add(j);
}
int[][] dp = new int[n + 1][N];
dp[0][0] = 1;
for (int k = 1; k <= n; ++k)
for (int i = 0; i < N; ++i)
for (int j : linked[i])
dp[k][i] += dp[k - 1][j];
for (int i = 0; i < N; ++i) ans += dp[n][i];
System.out.println(ans);
}
boolean check(int n, int k) {
int cnt = 0;
while (n > 0) {
if (n % K > 0) ++cnt;
else cnt = 0;
if (n % K >= k) return false;
if (cnt >= K) return false;
n /= K;
}
return true;
}
int leftAdd(int n, int m) {
int res = 0, k = 1, cnt = 0;
for (int t; n > 0 || m > 0; n /= 3, m /= 3, k *= K) {
t = n % K;
if (t > 0) {
++cnt;
t += m % K;
if (t >= K || cnt == K) return -1;
res += t * k;
} else cnt = 0;
}
return res;
}
}
离线打表
限制范围内的 N 、 M N、M N、M 都极小,可能的组合也只有 25 25 25 种,自然有一种朴素的解法,即我们先暴搜预处理出这 25 25 25 种组合对应的结果,然后编写程序直接输出即可。
下面程序直接将 A C \mathrm{AC} AC 代码复制到粘贴板了。
然后我就发现这道题枝剪深搜随便过,
I \mathrm I I 题这么出是真的没看懂。
import java.awt.*;
import java.awt.datatransfer.StringSelection;
public class Test {
public static void main(String[] args) { new Test().run(); }
int N = 5, M = 5, K = 3, buf;
boolean[][] X = new boolean[N + K + 1][M + K + 1];
void run() {
StringBuilder main = new StringBuilder();
main.append("import java.util.Scanner;\n\n");
main.append("public class Main {\n\n");
main.append(" public static void main(String[] args) { new Main().run(); }\n\n");
main.append(" int[][] ans = {{},\n");
for (int n = 1; n <= N; ++n) {
main.append(" {0");
for (int m = 1; m <= M; ++m) {
buf = 0;
dfs(n + K, m + K, K, K);
main.append(", ");
main.append(buf);
}
main.append("},\n");
}
main.append(" };\n\n");
main.append(" void run() {\n");
main.append(" Scanner in = new Scanner(System.in);\n");
main.append(" System.out.println(ans[in.nextInt()][in.nextInt()]);\n");
main.append(" }\n}");
Toolkit.getDefaultToolkit().
getSystemClipboard().
setContents(
new StringSelection(main.toString()), null);
}
void dfs(int n, int m, int i, int j) {
if (i == n) ++buf;
else {
if (j == m) dfs(n, m, i + 1, K);
else {
dfs(n, m, i, j + 1);
if (X[i - 1][j] && X[i - 2][j]) return;
if (X[i][j - 1] && X[i][j - 2]) return;
X[i][j] = true;
dfs(n, m, i, j + 1);
X[i][j] = false;
}
}
}
}
面向编程的编程。
试题 J: 分考场
时间限制: 10.0 s 10.0\mathrm s 10.0s 内存限制: 512.0 M B 512.0\mathrm{MB} 512.0MB 本题总分: 25 25 25 分
【问题背景】
古语有云 : : :春风得意马蹄疾,一日看尽长安花。
当然在一场考试中所有人都春风得意马蹄疾是不可能的,尤其是碰到一些毒瘤出题人的时候。
【问题描述】
又到了每月一次的月考,又是 x f \mathrm{xf} xf 老师出题。
上一次 x f \mathrm{xf} xf 老师出的题太毒瘤了,平均分只有 40 40 40 多,同学们都非常不满意,毕竟别的科的平均分都是 80 80 80 多。
这次 x f \mathrm{xf} xf 为了不被同学们寄刀片,想了一个办法:只公布所有考场的平均分的平均分。这样他就可以通过调整考场的分配方式,使得平均分显得高。(每个考场都可以容纳无限人)
每次考试也不是所有同学都参加的,只有学号在 [ l , r ] [l,r] [l,r] 这个区间中的同学会参加。
他想知道对于每次考试,他调整过考场后,所有考场的平均分的平均分的最大值。
当然,同学们也可能会努力学习或整日颓废使成绩发生改变。
【输入格式】
输入的第一行包含一个整数 n n n。
第二行包含 n n n 个整数,第 i i i 个数 v i v_i vi,表示开始时每个同学的成绩。
第三行包含一个整数 q q q,表示有 q q q 次操作。
之后 q q q 行,每行描述一个操作,第一个数表示操作类型。
如果操作为 1 p x 1\ p\ x 1 p x,表示学号为 p p p 的同学分数变为 x x x。
如果操作为 2 l r k 2\ l\ r\ k 2 l r k, 表示把学号在 [ l , r ] [l,r] [l,r] 中的同学分成 k k k 个考场,求这 k k k 个考场的平均分的平均分的最大值。
【输出格式】
对于每个 2 2 2 操作输出一行,四舍五入保留正好 3 3 3 位小数。
【样例输入】
5
5 3 4 2 1
5
2 1 4 3
1 4 8
2 3 5 3
1 2 2
2 1 3 2
【样例输出】
3.833
4.333
4.000
【样例说明】
第一个操作询问学号在 [ 1 , 4 ] [1, 4] [1,4] 之间的同学分成 3 3 3 个考场的平均分的平均分的最大值,最优策略是 : : : { 1 } , { 2 , 4 } , { 3 } \{1\}, \{2, 4\}, \{3\} {1},{2,4},{3},平均分是 5 1 + 3 + 2 2 + 4 1 3 \frac {\frac 51+\frac{3 + 2}2+\frac 41}3 315+23+2+14。
第二个操作把学号为 4 4 4 的同学的分数变为 8 8 8。
第三个操作询问学号在 [ 3 , 5 ] [3, 5] [3,5] 之间的同学分成 3 3 3 个考场的平均分的平均分的最大值,最优策略是 : : : { 3 } , { 4 } , { 5 } \{3\}, \{4\}, \{5\} {3},{4},{5}。
第四个操作把学号为 2 2 2 的同学分数变为 2 2 2。
第五个操作询问学号在 [ 1 , 3 ] [1, 3] [1,3] 之间的同学分成 2 2 2 个考场的平均分的平均分的最大值,最优策略是 : : : { 1 } , { 2 , 3 } \{1\}, \{2,3\} {1},{2,3}。
【评测用例规模与约定】
对于全部评测用列, n ≤ 200000 , q ≤ 200000 n ≤ 200000, q ≤ 200000 n≤200000,q≤200000, 任意时刻同学的分数 v i ≤ 1 0 9 , k ≤ r − l + 1 v_i ≤ 10^9,k ≤ r - l + 1 vi≤109,k≤r−l+1。
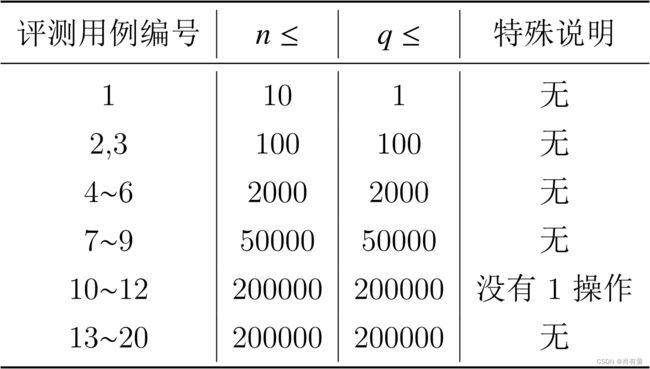
评测时将使用 10 10 10 个评测用例测试你的程序,每个评测用例的限制如下 : : :
贪心
考虑操作 2 2 2 的结果最优性,显然可以将操作 2 l r k 2\ l\ r\ k 2 l r k 对应的结果表示为: 1 k ∑ i = l r v i w i , ∑ i = l r w i = r − l + 1 \frac 1k\sum_{i = l}^r\frac {v_i}{w_i},\quad\sum_{i = l}^rw_i = r - l + 1 k1i=l∑rwivi,i=l∑rwi=r−l+1 也就是对于每一个操作 2 2 2,我们实质要做的操作是,将 r − l + 1 r-l+1 r−l+1 拆分成 k k k 个正整数之和作学号在 [ l , r ] [l,r] [l,r] 间的同学的成绩的除数( w i w_i wi 作 w i w_i wi 次),使得商之和最大,显然将 k − 1 k - 1 k−1 个 1 1 1 分配给成绩最高的 k − 1 k-1 k−1 名同学时,除非交换成绩相同的同学,不然无论如何都会使商之和变小,此时即为找到一个最优解。
还有就是 n 、 q n、q n、q 的规模都很大,若是使用比较型排序求出 1 ∼ k − 1 1 \sim k - 1 1∼k−1 大,最坏复杂度在 O ( q n log n ) O(qn\log n) O(qnlogn) 显然会超时,但我们只需要知道 1 ∼ k − 1 1 \sim k - 1 1∼k−1 大的和,以及学号在 [ l , r ] [l,r] [l,r] 间的同学的成绩的和,容易想到树状数组套动态开点权值线段树二分第 k k k 大将复杂度优化至 O ( q log 2 n ) O(q\log^2 n) O(qlog2n),不过考虑到时间足足有 10 s 10\mathrm s 10s 秒,随机构造的数据下 b f \mathrm{bf} bf 都绰绰有余了。
下面给出数据结构嵌套的解法,希望基础薄弱的读者斟酌后阅读。
不过也不一定对。
import java.io.*;
public class Main {
public static void main(String[] args) { new Main().run(); }
int n, N = 200001, inf = (int)1e9, cur = 0;
void run() {
PrintWriter out = new PrintWriter(System.out);
n = nextInt();
for (int i = 1; i <= n; ++i) root[i] = ++cur;
for (int i = 1; i <= n; ++i)
add(i, v[i] = nextInt(), 1);
int n, m, opt, l, r, K, k, g;
long s1, s2;
for (int q = nextInt(); q > 0; --q) {
opt = nextInt();
l = nextInt();
r = nextInt();
if (opt == 1) {
add(l, -v[l], -1);
add(l, v[l] = r, 1);
} else {
k = nextInt();
g = r - l + 1;
s1 = s2 = n = m = 0;
for (; r > 0; r &= r - 1) {
rbuf[n++] = root[r];
s1 += tsum[r];
}
for (--l; l > 0; l &= l - 1) {
lbuf[m++] = root[l];
s1 -= tsum[l];
}
K = k;
l = 0;
r = inf;
while (l < r) {
int tot = 0;
long buf = 0;
for (int i = 0; i < n; ++i) {
tot += cnt[rs[rbuf[i]]];
buf += sum[rs[rbuf[i]]];
}
for (int i = 0; i < m; ++i) {
tot -= cnt[rs[lbuf[i]]];
buf -= sum[rs[lbuf[i]]];
}
if (K > tot) {
s2 += buf;
K -= tot;
r = l + r >> 1;
for (int i = 0; i < n; ++i) rbuf[i] = ls[rbuf[i]];
for (int i = 0; i < m; ++i) lbuf[i] = ls[lbuf[i]];
} else {
l = l + r + 2 >> 1;
for (int i = 0; i < n; ++i) rbuf[i] = rs[rbuf[i]];
for (int i = 0; i < m; ++i) lbuf[i] = rs[lbuf[i]];
}
}
out.printf("%.3f\n", (s2 + (double)(s1 - s2) / (g - k + 1)) / k);
}
}
out.flush();
}
int[] root = new int[N], v = new int[N], ls = new int[N << 4], rs = new int[N << 4], cnt = new int[N << 4], lbuf = new int[32], rbuf = new int[32];
long[] sum = new long[N << 4], tsum = new long[N];
void add(int i, int a, int k) {
while (i <= n) {
update(root[i], 0, inf, a, k);
tsum[i] += a;
i += i & -i;
}
}
void update(int rt, int l, int r, int a, int k) {
cnt[rt] += k;
sum[rt] += a;
if (l < r) {
int mid = l + r >> 1;
if (a <= mid) {
if (ls[rt] == 0) ls[rt] = ++cur;
update(ls[rt], l, mid, a, k);
} else {
if (rs[rt] == 0) rs[rt] = ++cur;
update(rs[rt], mid + 1, r, a, k);
}
}
}
StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}