KMP算法详解 通俗易懂
概述
KMP算法要解决的问题就是在字符串（也叫主串）中的模式（pattern）定位问题。
我现在有两个字符串，我们是否可以判断出其中的一个是另一个字符串的字串，如：
ABCD是否为QWEABCJE的字串，显然并不是它的字串，因为必须是连续匹配的，中间不能被分割。
通常我们以前的做法就是暴力解法，设置两个指针，不匹配时主串的指针就往后走，当发现一个匹配时，字串和主串的指针就开始一起动，如果发现字串还没到结尾却突然两个字符串不相等时，子串就必须回溯到第一个字符，主串也回溯到上一次的字符的下一个位置重新开始找第一个匹配的字符……。
但如果我给的两个字符串比较极端如："111111112"、"1112"，这时就会疯狂回溯，时间复杂度就是O(N×M)，NM是字符串的长度。
KMP算法
KMP刚开始也是和暴力递归一样，从左往右依次考查每一个开头，主串的某一个位置开头如果能匹配子字符串，则返回该位置，但是对此做了优化。
1.求出next数组
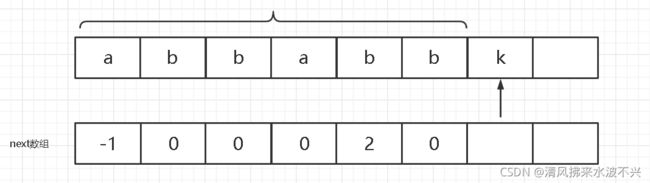
也就是求出子字符串第K个字符前面的所有字符(0~k-1)的最长的前缀和后缀的最大匹配长度
入图，子字符串为abbabbk，我们从0开始，第0个字符前面没有字符了就规定为-1；下一个是一号元素为b，b前面只有一个a，因为前缀和后缀不能取相同的整体(否则必相等)，所以b为0；再是2号元素也是b，此时前缀取1位为a，后缀也取1位为b不相等，不能取2了，所以也为0……
再来看K，因为前后缀各取3位且相等，且在所有(虽然在本例没有)相等的里面3最大，所以取3
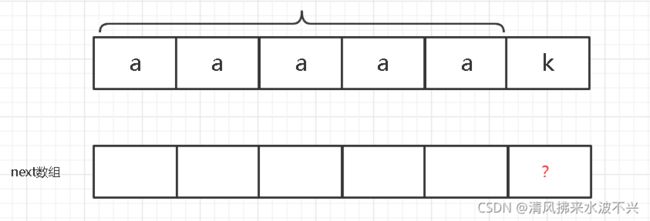
在看一个例子
子数组为次，怎么求问号的数字？ 如下？为4
我们需要求出所有的子字符串的前缀、后缀的最大匹配长度以构成一个next数组
2.步骤
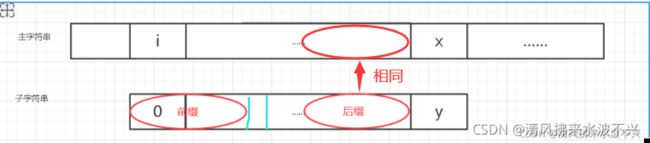
加入下图的子字符串从0位置到y-1位置一路都和主字符串i位置到x-1位置都相等，但是x和y位置又不相等了，按照经典算法，此时我要回溯回去，子字符串要重新从0开始和主字符串的i+1位置开始重新匹配，是吗？
KMP算法是这样做的，我们已经知道了y位置的前缀和后缀的最大匹配长度，假如就是下面的，前缀和后缀肯定是相同的。
此时你可以找出，既然前缀和后缀必然相同，那么下面的等式也必然相同，因为刚刚已经顺利的匹配过他两了，确认相同才走到x和y的位置，所以也就有了前缀和主字符串的那一块也相等。
因此我们就没必要在去重复匹配了，此时子字符串的指针就直接来到前缀后面那个绿色的地方即可，继续和主字符串的x的位置往后开始比较。就是把子字符串移过去了一样。
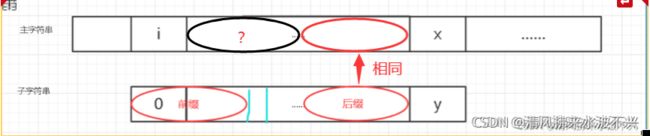
还有个问题就是，你一下子移动了这么多步，你怎么知道中间还有没有匹配的呢？中间可能匹配的是不是被漏掉了啊？也就是下图中黑色圆圈的未知区域被省掉了
3.证明
我来证明证明这中间的一部分位置无论如何都是匹配不出的
用以前的图来证明，前缀和后缀等都是一样的，只是移动了位置，如果K那个位置可以和子字符串相匹配，那么绿色圈里面的数据肯定是相等的吧。
然而，我们以前推论过，x和y前面一路都是相等的，再x和y的位置才不相等停下来，这也就突然又多了一个圈，多加的那个区域和主字符串的绿色区域相等，又因为 两个绿色区域是相等的，所以子字符串的两个区域也相等，这就出问题了，因为他们相等而且比我们以前求得y的最大前缀和后缀相等的区域大，所以就矛盾了。
所以你可以大胆的跳。
4.例子
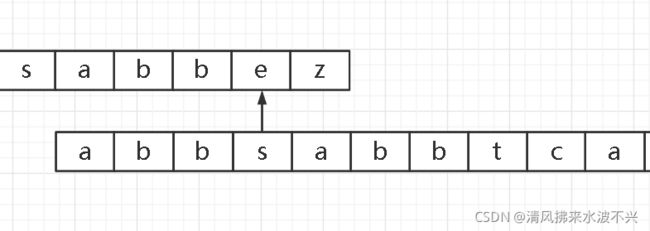
先拿个例子来看看是如何实现的，有下面两个字符串，此时前面的都相等，现在已近匹配到e和w不相等，现在得到w的next数组里的值为7
所以子字符串移动到第7个索引位置，也就是t，与主字符串的e开始重新比较
发现还是不相等，再得到t位置的next数组值为3，重新回到索引为3的位置，即s
还是不相等，但是s位置的next数组值此时为0，此时从头开始，即a开始
不相等，但是已经到头了为-1不能再移了，然后主字符串移动一个位置到z开始和子字符串重新开始比较……
5.求next数组
现在最后一步即我们的next数组怎么求出来，可以找出规律： 0号位置恒定-1，1号为0
假设我现在要求空白位置的next值，则看看前一个字符？的next值为多少(已经求出)，它是6，因此我们从数组的6号元素和？相比较，如果6号即b和？相等，则空白处的next值等于？的next值+1，如果不相等，则跳到6号元素的next值的位置即2号位置和？比较，如果相等就等于2+1，
如果不想等就继续跳，直到跳到0位置和？比，如果还不相等就为0；和前面的证明一样
代码如下：
public int[] getNext(char[] s) {
int[] next = new int[s.length];
next[0] = -1;
if (s.length == 1) return next;
next[1] = 0;
int cn = 0;//和i-1比的下标
int i = 2;
while (i < next.length) {
if (s[i - 1] == s[cn]) {
next[i++] = ++cn; //代表匹配成功，+1操作
} else if (cn > 0) {//不匹配，跳到前面再比较
cn = next[cn];
} else {
next[i++] = 0;//不能再跳了
}
}
return next;
}代码
public int KMP(String s1, String s2) {
char[] c1 = s1.toCharArray();
char[] c2 = s2.toCharArray();
int[] next = getNext(c2);
int i = 0, j = 0;
while (i < c1.length && j < c2.length) {
if (c1[i] == c2[j]) {
i++;
j++;
} else if (next[j] == -1) {//子字符串到头了,或者写成j==0
i++;
} else {
//子字符串回溯到next的位置
j = next[j];
}
}
//如果子字符串到末尾了，则从主字符串的当前位置减去子字符串的长度得到正确开始匹配的结果
return j == c2.length ? i - j : -1;
}总结
现在主串的长度位N，子串的长度为M，getNext函数的时间复杂度为O(M)，KMP函数的时间复杂度除去getNext也就是O(N)，因为N>M所以KMP算法的时间复杂度为O(N)