NewOJ 2022 Contest 1题解

比赛链接：http://oj.ecustacm.cn/contest.php?cid=1023

题目总览

题目	TAG	难度	补题链接
质数	质数	☆	http://oj.ecustacm.cn/problem.php?id=1700
01卡片	模拟、$DP$	☆☆	http://oj.ecustacm.cn/problem.php?id=1701
数位和	模拟、枚举	☆☆	http://oj.ecustacm.cn/problem.php?id=1702
地图	$dfs$、记忆化搜索	☆☆☆	http://oj.ecustacm.cn/problem.php?id=1703
消消乐	模拟	☆☆	http://oj.ecustacm.cn/problem.php?id=1704
完美数组	二分答案	☆☆☆	http://oj.ecustacm.cn/problem.php?id=1705
窗户	模拟、枚举	☆☆☆	http://oj.ecustacm.cn/problem.php?id=1706
寻宝	最短路	☆☆☆☆	http://oj.ecustacm.cn/problem.php?id=1707
传送阵	动态规划、树状数组	☆☆☆☆	http://oj.ecustacm.cn/problem.php?id=1708

A 质数

题意：

Tag： 质数

难度： ☆

思路： 从$20222022$开始往上枚举即可。由于质数密度很大，所以最多找几十次就会出现质数。

#include
using namespace std;
bool is_prime(int x)//素数判断
{
    if(x <= 1)return false;
    for(int i = 2; i * i <= x; i++)
        if(x % i == 0)return false;
    return true;
}
int main()
{
    for(int i = 20222022; ; i++)
    {
        if(is_prime(i))
        {
            cout<<i<<endl;
            break;
        }
    }
    return 0;
}

B 01卡片

题意：

Tag： 模拟、$DP$

难度： ☆☆

思路： 填空题：直接暴力模拟即可，最终输出答案。直接提交可能会超时，可以本地算出答案后提交结果。

#include
using namespace std;
int main()
{
    int num_1 = 0, num_0 = 0;
    for(int i = 1; i <= 20222022; i++)
    {
        int x = i;
        while(x){
            if(x&1)num_1++;
            else num_0++;
            x >>= 1;
        }
    }
    cout<<num_0<<" "<<num_1<<endl;
    return 0;
}

进阶做法：

考虑$dp[n]$表示$1-n$二进制表示中数字$0$的数量。

例如$1-6$中二进制，记$s[i]$表示$i$的二进制表示中0的数量：

数字	二进制	奇偶性	$s$
1	1	奇	0
2	10	偶	1
3	11	奇	0
4	100	偶	2
5	101	奇	1
6	110	偶	1

$dp[6]=(S[1]+S[3]+S[5])+(S[2]+S[4]+S[6])$

其中$1$、$3$、$5$末尾均为$1$，对$0$没有贡献，则有
$$S[1]+S[3]+S[5]=S[0]+S[1]+S[2]=dp[2]$$

其中$2$、$4$、$6$末尾均为$0$，对$0$的贡献为$3$次，则有：
$$S[2]+S[4]+S[6]=3+S[1]+S[2]+S[3]=3+dp[3]$$

相当于$dp[6]=3+dp[2]+dp[3]$，扩展一下，对于所有的偶数有：
$$dp[n]=dp[n/2]+dp[n/2-1]+n/2$$
类似的对于奇数有：
$$dp[n]=2\ast dp[n/2]+n/2$$
此处的除法均为向下取整。

类似地，对于$1$的个数也可以类似计算，这样就可以在$O(log(n))$时间内求解$1-n$的二进制中$0$的个数和$1$的个数。

#include
using namespace std;
int Zero(int x)
{
    if(x <= 1)return 0;
    if(x & 1) return 2 * Zero(x / 2) + x / 2;
    else return Zero(x / 2) + Zero(x / 2 - 1) + x / 2;
}
int One(int x)
{
    if(x <= 1)return x;
    if(x & 1) return 2 * One(x / 2) + x / 2 + 1;
    else return One(x / 2) + One(x / 2 - 1) + x / 2;
}
int main()
{
    cout<<Zero(20222022)<<" "<<One(20222022)<<endl;
    return 0;
}

C 数位和

题意：

Tag： 模拟、枚举

难度： ☆☆

思路： 根据题意写出$f$函数和$s$函数，对于$1-2022$每个数字先计算出每个数字的$s$值。

然后暴力枚举$x$、$y$、$z$即可。本地计算结果，提交答案。

也可以在枚举过程中剪枝，例如$s[x]$至少大于等于$3$，使得提交暴力枚举的代码也不会超时。

存在线性复杂度的做法，提示：前缀和。

#include
using namespace std;

int f(int x)
{
    if(x < 10)return 0;
    int ans = 0;
    while(x)ans += x % 10, x /= 10;
    return ans;
}
int s(int x)
{
    int ans = 0;
    while(x)
    {
        ans++;
        x=f(x);
    }
    return ans;
}
int a[3000];
int main()
{
    for(int i = 1; i <= 2022; i++)
        a[i] = s(i);
    int ans = 0;
    for(int x = 2022; x >= 1; x--)if(a[x] >= 3)
        for(int y = x - 1; y >= 1; y--)if(a[x] > a[y] && a[y] >= 2)
            for(int z = y - 1; z >= 1; z--)if(a[y] > a[z])
                ans++;
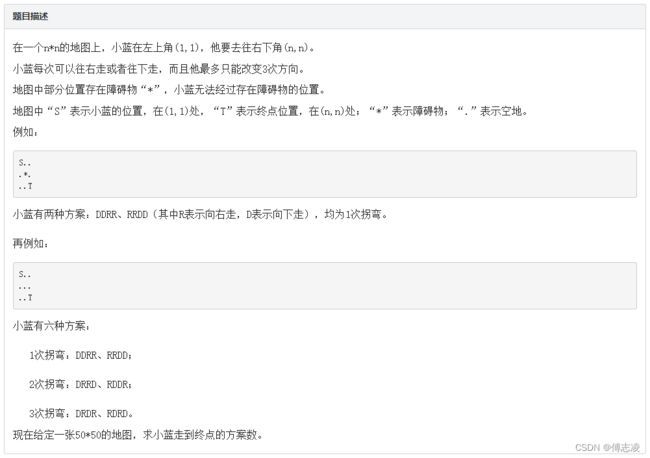
    cout<<ans<<endl;
    return 0;
}

D 地图

题意：

Tag： $dfs$、记忆化搜索

难度： ☆☆☆

思路： 从起点到终点最多改变$3$次方向，那么在搜索的过程中还需要额外维护当前方向、目前已经转弯次数。

记$dp[i][j][k][dir]$表示起点为$(i,j)$，已经经历过$3$次转弯，当前方向为$dir$的方案数。

1. $dir$向右时：$dp[i][j][k][dir]=dp[i][j+1][k][dir]+dp[i+1][j][k+1][!dir]$
2. $dir$向下时：$dp[i][j][k][dir]=dp[i][j+1][k+1][!dir]+dp[i+1][j][k][dir]$

边界：

1. $i,j$越界、转弯次数超过$3$次、障碍物时，方案数均为$0$
2. $i=j=n$，方案数为$1$

使用$dfs$+记忆化搜索求出$dp$数组即可。

注意提交时只输出答案。

#include
using namespace std;
int n, k;
char Map[55][55];
int dir[][2] = {0, 1, 1, 0};
int dp[55][55][2][4];
int dfs(int x, int y, int d, int step)
{
    if(x > n || y > n)return 0;     //越界
    if(Map[x][y] == '*')return 0;   //障碍物
    if(step > k)return 0;           //转弯次数超过k
    if(x == n && y == n)return 1;   //终点
    if(dp[x][y][d][step])return dp[x][y][d][step];  //记忆化搜索
    int ans = 0;
    for(int i = 0; i <= 1; i++)     //两种方向
        ans += dfs(x + dir[i][0], y + dir[i][1], i, step + (i != d));
    return dp[x][y][d][step] = ans;
}

int main()
{
    n = 50;
    k = 3;
    for(int i = 1; i <= n; i++)cin >> (Map[i] + 1);
    memset(dp, 0, sizeof(dp));
    int ans = 0;
    if(Map[1][2] != '*')ans += dfs(1, 2, 0, 0);
    if(Map[2][1] != '*')ans += dfs(2, 1, 1, 0);
    cout<<ans<<endl;
    return 0;
}

E 消消乐

题意：

Tag： 模拟

难度： ☆☆

思路： 直接模拟即可，用两个数组$X[i]$，$Y[i]$记录数字$i$所在的行和列。同时用两个数组$Sx$、$Sy$记录每行、每列剩余的数字数量。

当$Sx,Sy$在模拟过程中出现了$0$，此时输出答案即可。

#include
using namespace std;
int X[10005], Y[10005];
int Sx[105], Sy[105];

int main()
{
    int n, x;
    cin >> n;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            cin >> x, X[x] = i, Y[x] = j;
    for(int i = 1; i <= n; i++)
        Sx[i] = Sy[i] = n;
    for(int i = 1; i <= n * n; i++)
    {
        cin >> x;
        Sx[X[x]]--, Sy[Y[x]]--;
        if(!Sx[X[x]] || !Sy[Y[x]]){
            cout<<x<<endl;break;
        }
    }
    return 0;
}

F 完美数组

题意：

Tag： 二分答案

难度： ☆☆☆

思路： 可以发现，删去的数字越多，越容易变成完美数组。

这说明答案存在单调性，利用二分答案，假设最小代价为$x$，则可以直接将两个数组中所有小于等于$x$的数字全部删除，直接根据完美数组的定义$O(n)$判断即可。

总的时间复杂度$O(nlog(m))$，其中$m$为数组元素中最大值。

#include
using namespace std;
const int maxn = 1e6 + 10;
int n, a[maxn], b[maxn];
//判断将所有小于等于x的数组删除后，能否使得两个数组都变成完美数组
bool check(int x)
{
    bool first = true;  //判断是否两两配对
    int pre;            //前一个的数值
    for(int i = 1; i <= n; i++)
        if(a[i] > x)
        {
            if(first)first = false, pre = a[i];
            else {
                if(pre != a[i])return false;
                first = true;
            }
        }
    if(!first)return false;
    for(int i = 1; i <= n; i++)
        if(b[i] > x)
        {
            if(first)first = false, pre = b[i];
            else {
                if(pre != b[i])return false;
                first = true;
            }
        }
    if(!first)return false;
    return true;
}
int main()
{
    scanf("%d", &n);
    int ans = 0, left = 0, right = 0;
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]), right = max(right, a[i]);
    for(int i = 1; i <= n; i++)
        scanf("%d", &b[i]), right = max(right, b[i]);
    while(left <= right)    //二分答案
    {
        int mid = (left + right) >> 1;
        if(check(mid))ans = mid, right = mid - 1;
        else left = mid + 1;
    }
    printf("%d\n", ans);
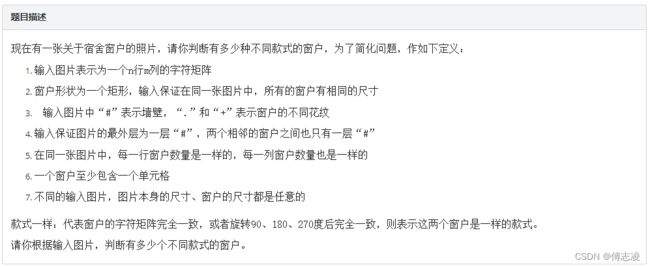
    return 0;
}

G 窗户

题意：

Tag： 模拟、枚举

难度： ☆☆☆

思路： 首先需要找出窗户的位置。根据题目定义，假设窗户左上角为$(i,j)$，则有$(i-1,j-1),(i-1,j),(i,j-1)$均为$\#$。

据此可以找出所有窗户的左上角，然后对于每个窗户找出这个窗户的长和宽。

不同的窗户需要判断是否相同，可以用set去重。每个窗户有4种旋转表示，选择最小的字典序作为窗户的唯一表示。

#include
using namespace std;
int n, m;
char Map[125][125];
char s[125][125];

void Rotate(int n, int m)
{
    char tmp[125][125];
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            tmp[i][j] = s[i][j];
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            s[j][n + 1 - i] = tmp[i][j];
}

//将左上角为(x,y)的窗户变成string
string canonize(int x, int y)
{
    int xx = x, yy = y;//右下角坐标(xx, yy)
    while(xx + 1 <= n && Map[xx + 1][y] != '#')
        xx++;
    while(yy + 1 <= m && Map[x][yy + 1] != '#')
        yy++;
    //将窗户拷贝到tmp中
    for(int i = x; i <= xx; i++)
        for(int j = y; j <= yy; j++)
            s[i - x + 1][j - y + 1] = Map[i][j];
    string ans;
    int n = xx - x + 1, m = yy - y + 1;
    for(int _ = 1; _ <= 4; _++)//四次旋转
    {
        string now;
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
                now += s[i][j];
            now += '#';
        }
        if(ans.size() == 0 || now < ans)
            ans = now;
        //将tmp数组旋转90度
        Rotate(n, m);
        swap(n, m);
    }
    return ans;
}
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        cin >> (Map[i] + 1);
    set<string>s;//存储所有窗户
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        if(Map[i - 1][j - 1] == '#' && Map[i][j - 1] == '#' && Map[i - 1][j] == '#')
            s.insert(canonize(i, j));
    cout<<s.size()<<endl;
    return 0;
}

H 寻宝

题意：

Tag： 最短路

难度： ☆☆☆☆

思路： 首先将所有红宝石的点连到点$S$、 所有蓝宝石的点连到$T$，题目变成找一个连通块，正好从$1$出发，包含$S$和$T$。

也就相当于找一条路径，路径的起点是$1$，终点有两个，分别为$S$和$T$，求最短路。

这个所有的最短路相当于一个$Y$字形的岔路，底部为起点$1$，上面分别为$S$和$T$，前半部分可以重叠。

可以枚举分叉点，对于每个分叉点$i$，需要求解$1$到$i$、$i$到$S$、$i$到$T$的最短路。

相当于需要求出$1$到所有点、所有点到$S$、所有点到$T$的最短路。

三次$dijkstra$预处理出三个距离即可，对于后面两次$dijkstra$，需要在反向图上进行求解。

#include
using namespace std;
const int INF = 1e9 + 7;
const int maxn = 1e5 + 10;
struct edge
{
    int v, w;
    edge(){}
    edge(int v, int w):v(v), w(w){}
};
struct Heapnode
{
    int u, d;
    Heapnode(){}
    Heapnode(int u, int d):u(u), d(d){}
    bool operator < (const Heapnode& a)const
    {
        return d > a.d;
    }
};
vector<edge>G[maxn];
vector<edge>rG[maxn];
bool vis[maxn];
int d1[maxn], d2[maxn], d3[maxn];
int n, m, k;
void add(int u, int v, int w)
{
    G[u].push_back(edge(v, w));
    rG[v].push_back(edge(u, w));
}
void dijkstra(int s, int d[], vector<edge>G[])
{
    for(int i = 1; i <= n + 2; i++)
        vis[i] = 0, d[i] = INF;
    priority_queue<Heapnode>q;
    q.push(Heapnode(s, 0));
    d[s] = 0;
    while(!q.empty())
    {
        Heapnode now = q.top();
        q.pop();
        int u = now.u;
        if(vis[u])continue;
        vis[u] = 1;
        for(auto x : G[u])
        {
            int v = x.v, w = x.w;
            if(d[v] > d[u] + w)
            {
                d[v] = d[u] + w;
                q.push(Heapnode(v, d[v]));
            }
        }
    }
}
int main()
{
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= m; i++)
    {
        int x;
        scanf("%d", &x);
        add(x, n + 1, 1);
    }
    for(int i = 1; i <= k; i++)
    {
        int x;
        scanf("%d", &x);
        add(x, n + 2, 1);
    }
    for(int u = 1; u <= n; u++)
    {
        int k, v;
        scanf("%d", &k);
        while(k--)
        {
            scanf("%d", &v);
            add(u, v, 1);
        }
    }
    dijkstra(1, d1, G);
    dijkstra(n + 1, d2, rG);
    dijkstra(n + 2, d3, rG);
    long long ans = INF;
    for(int i = 1; i <= n; i++)
        ans = min(ans, (long long)d1[i] + d2[i] + d3[i]);
    if(ans == INF)puts("impossible");
    else printf("%lld\n", ans - 2);
    return 0;
}

I 传送阵

题意：

Tag： 动态规划、树状数组

难度： ☆☆☆☆

思路： 如果不存在传送门，到达终点的距离为$2\ast n$，如果使用第$i$个传送门，可以节省传送门传送的距离，即从起点到终点的距离。

$dp[i]$表示前$i$个传送门中，使用第$i$个传送门可以省下最大的距离。

根据$dp$定义可以找出状态转移方程：
$$\begin{array}{rl}dp[i]& =max\{dp[j]+x2[i]-x1[i]+y2[i]-y1[i]\}=max\{dp[j]+dis[i]\}\\ j满足& ：x2[j]\le x1[i],y2[j]\le y1[i]\end{array}$$$dis$数组在读入时计算。

可以在$O(n^2)$的时间复杂度暴力转移，从$j$到$i$要满足$j$的终点小于等于$i$的起点。

二维约束条件下的动态规划，可以使用数据结构（树状数组、线段树）进行优化。

将传送门拆成两个点，按照$x$作为第一关键字，$y$作为第二关键字，这样排序后，可以确保$x$递增，后续只需判断$y$的相对大小。

对于起点：当前起点的$x$肯定比之前的$x$大，只要判断比当前的$y$小的终点的dp最大值，可以使用树状数组维护前缀最大值。

使用树状数组时需要对$y$坐标进行离散化。

对于终点：只需要把对应$dp$值放入树状数组即可。

#include
#define lowbit(x) ((x) & (-x))
using namespace std;
const int INF = 1e9 + 7;
const int maxn = 2e5 + 10;
typedef long long ll;
int n, m, tot;
struct node
{
    int x, y;
    int idx, tag;
}a[maxn];
int b[maxn];
bool cmp(node a, node b)
{
    return a.x < b.x || a.x == b.x && a.y < b.y;
}
ll tree[maxn], dp[maxn], dis[maxn];
//树状数组维护前缀最小值
ll query(int x)
{
    ll ans = 0;
    while(x)
        ans = max(ans, tree[x]), x -= lowbit(x);
    return ans;
}
void update(int x, ll d)
{
    while(x < maxn)
        tree[x] = max(tree[x], d), x += lowbit(x);
}
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++)
    {
        ++tot;
        scanf("%d%d", &a[tot].x, &a[tot].y);
        a[tot].idx = i;
        a[tot].tag = 0;//起点
        dis[i] -= a[tot].x + a[tot].y;
        ++tot;
        scanf("%d%d", &a[tot].x, &a[tot].y);
        a[tot].idx = i;
        a[tot].tag = 1;//终点
        dis[i] += a[tot].x + a[tot].y;
    }
    sort(a + 1, a + 1 + tot, cmp);
    //y坐标值进行离散化
    int cnt = 0;
    for(int i = 1; i <= tot; i++)
        b[++cnt] = a[i].y;
    sort(b + 1, b + 1 + cnt);
    cnt = unique(b + 1, b + 1 + cnt) - (b + 1);
    for(int i = 1; i <= tot; i++)
        a[i].y = lower_bound(b + 1, b + 1 + cnt, a[i].y) - b;

    //更新dp
    for(int i = 1; i <= tot; i++)
    {
        if(a[i].tag == 0)//起点
            dp[a[i].idx] = query(a[i].y) + dis[a[i].idx];
        else
            update(a[i].y, dp[a[i].idx]);
    }
    ll ans = 2 * n;
    for(int i = 1; i <= m; i++)
        ans = min(ans, 2LL * n - dp[i]);
    cout<<ans<<endl;
    return 0;
}