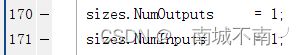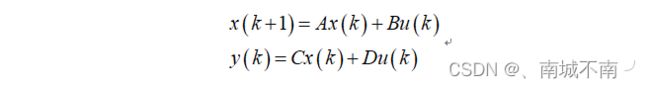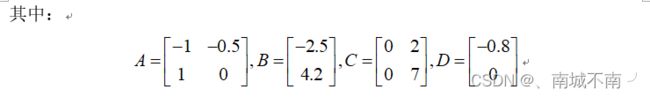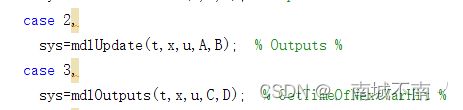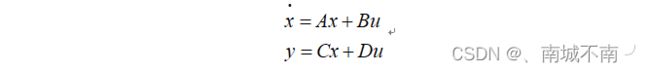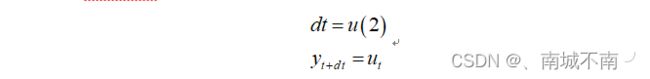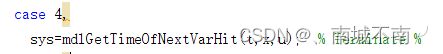S-function的使用
说明:《MATLAB/Simulink系统仿真超级学习手册》石良臣 matlab2018a——仅作为笔记。
S-function使用说明
相关概念
1、直接馈通
2、动态维矩阵
3、采样时间和偏移量
(1)连续采样时间
(2)连续但微步长固定采样时间
(3)离散采样时间
(4)可变采样时间
(5)继承采样时间
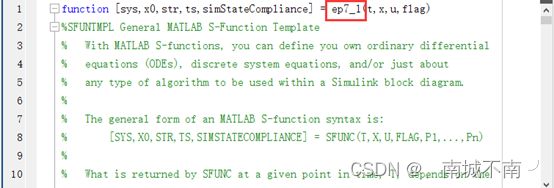
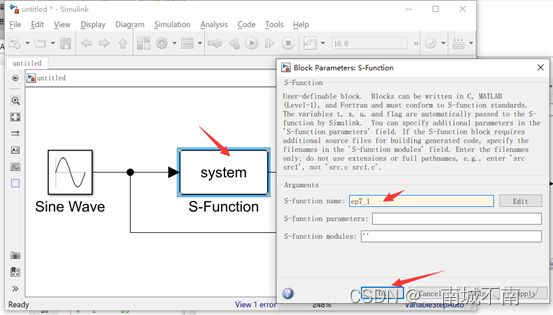
例7-1 y=2u
7.1.5向S-function传递参数
注:使用S-function parameters 区域输入用户自定义参数。
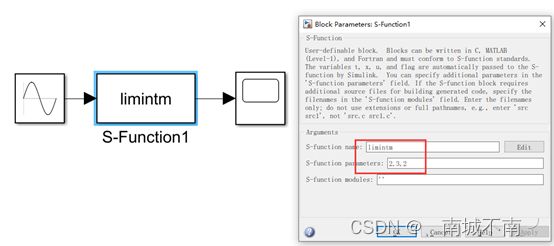
使用范例limintm。
三个参数:上边界、下边界、初始条件。
7.1.6何时使用S-function
包括:
- 向simulink中增加一些新的通用模块;
- 增加作为硬件设备驱动程序的模块;
- 将已有的C代码组合到仿真中;
- 使用一组数据方程式来对系统进行描述;
- 使用可视化动作;
7.2 工作原理
Simulink模块包括:一组输入、一组状态、一组输出。输出位采样时间、输入和模块状态的函数。
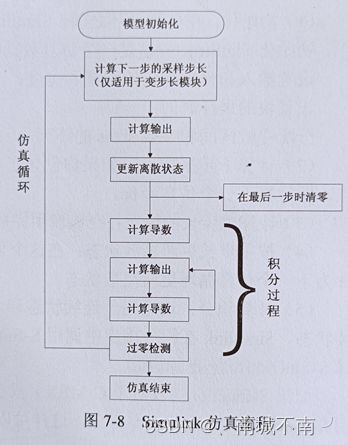
7.2.3 S-function仿真流程
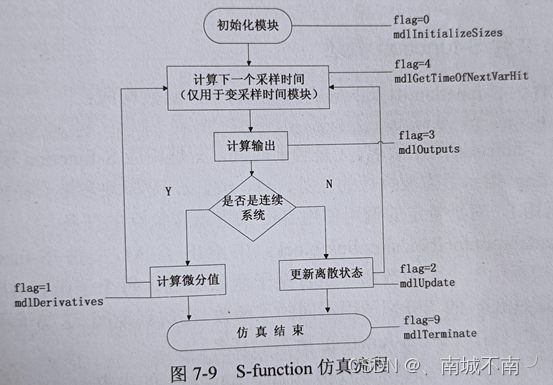
S-function包含主函数和6个功能子函数:mdlInitializeSizes初始化、mdlDerivatives连续状态微分、mdlUpdate离散状态更新、mdlOutputs模块输出、mdlGetTimeOfNextVarHit计算下次采样时刻、mdlTerminate仿真结束。
Flag:仿真流程标志向量。
7.2.4 S-function回调程序
执行的任务:
- 初始化;
- 计算下步采样点;
- 计算主步长的输出;
- 按主步长更新离散状态;
- 计算积分。
7.3 编写M文件S-function
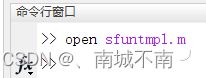
自带模板:open sfuntmpl.m
函数:
[sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag,p1,pl,…)注释:t——时间;x——状态向量;u——块的输入;flag——执行的任务;p1,pl,…——模块参数。
7.3.3 S-function的输出
sys——一个通用的返回参数。
x0——初始状态(除flag=0外,其余忽略)
str——保留以后使用。
ts——一个两列的矩阵。(采样时间、偏移量)
每个时间步(连续采样时间)都运行【0,0】;按照连接块的速率运行【-1,0】;仿真开始的0.1秒后每0.25秒(离散采样时间)运行一次【0.25,0.1】;
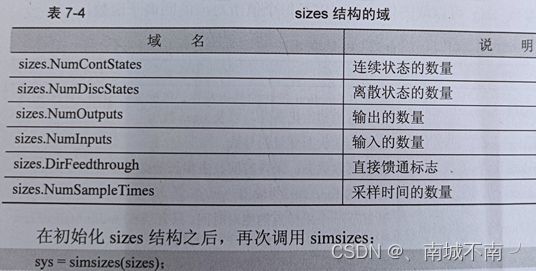
7.3.4定义S-function的模块特性
sizes = simsizes;%%返回一个未初始化的sizes结构。
7.3.5 M文件S-function实例
程序:
function [sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag)
%主函数
%主函数包含四个输出:
% sys数组包含某个子函数返回的值
% x0为所有状态的初始化向量
% str是保留参数,总是一个空矩阵
% Ts返回系统采样时间
%函数的四个输入分别为采样时间t、状态x、输入u和仿真流程控制标志变量flag
%输入参数后面还可以接续一系列的附带参数simStateCompliance
%注意:编写自己的S-function时,应该把函数名sfuntmpl改为S-function中对应的名字
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
%主函数结束
%% %下面是各个子函数,即各个回调过程
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
%初始化回调子函数
%提供状态、输入、输出、采样时间数目和初始状态的值
%初始化阶段,标志变量flag首先被置为0,S-function首次被调用时
%该子函数首先被调用,且为S-function模块提供下面信息
%该子函数必须存在
sizes = simsizes; %生成sizes数据结构,信息被包含在其中
sizes.NumContStates = 0; %连续状态数,缺省为0
sizes.NumDiscStates = 0; %离散状态数,缺省为0
sizes.NumOutputs = 0; %输出个数,缺省为0
sizes.NumInputs = 0; %输入个数,缺省为0
sizes.DirFeedthrough = 1; %是否存在直馈通道,1表示存在,0表示不存在
sizes.NumSampleTimes = 1; %采样时间个数,至少是一个
sys = simsizes(sizes); %返回size数据结构所包含的信息
x0 = []; %设置初始状态
str = []; %保留变量置空
ts = [0 0]; %设置采样时间
simStateCompliance = 'UnknownSimState';
function sys=mdlDerivatives(t,x,u)
%计算导数回调子函数
%给定t,x,u计算连续状态的导数,可以在此给出系统的连续状态方程
%该子函数可以不存在
sys = []; %sys表示状态导数,即dx
%%
function sys=mdlUpdate(t,x,u)
%状态更新回调子函数
%给定t、x、u计算离散状态的更新
%每个仿真步内必然调用该子函数,不论是否有意义
%除了在此描述系统的离散状态方程外,还可以在此添加其他每个仿真步内都必须执%行的代码
sys = []; %sys表示下一个离散状态,即x(k+1)
%%
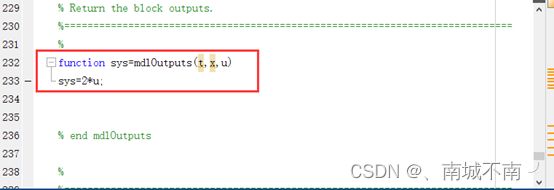
function sys=mdlOutputs(t,x,u)
%计算输出回调函数
%给定t,x,u计算输出,可以在此描述系统的输出方程
%该子函数必须存在
sys = []; %sys表示输出,即y
%%
function sys=mdlGetTimeOfNextVarHit(t,x,u)
%计算下一个采样时间
%仅在系统是变采样时间系统时调用
sampleTime = 1; %设置下一次采样时间是在1s以后
sys = t + sampleTime; %sys表示下一个采样时间点
%%
function sys=mdlTerminate(t,x,u)
%仿真结束时要调用的回调函数
%在仿真结束时,可以在此完成仿真结束所需的必要工作
sys = [];
例子7-2 用S-function实现Gain增益模块
1、将模板sfuntmpl.m另存为ep7_2.m,并修改主函数定义,增加新的输出参数gain,修改函数名为ep7_2。
function [sys,x0,str,ts,simStateCompliance] = ep7_2(t,x,u,flag,gain)2、增益参数是用来计算输出值的,所以需要对mdlOutput的调用进行修改;
case 3,
sys=mdlOutputs(t,x,u,gain);
3、修改mdlInitializeSizes初始化回调子函数。
设置输入输出个数均为1。
4、修改mdlOutputs子函数。
function sys=mdlOutputs(t,x,u,gain)
%计算输出回调函数
sys = gain * u;
5、保存ep7_2.m,建立系统模型。
补充:可以封装,
6、运行仿真。
2、用S-function实现离散系统。
例7-3 用S-function实现单位延迟。
单位延迟的差分方程为:
y(k+1)=u(k)
这相当于在每个仿真步长对采样做一阶保持。等价的状态方程表达为
x(k+1)=u(k)
y(k)=x(k)
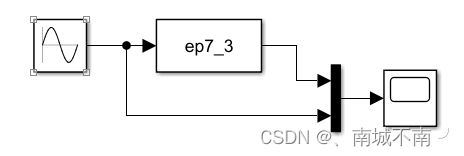
(1)将模板sfuntmpl.m另存为ep7_3.m,并修改主函数名为ep7_3。
命令行:open sfuntmpl.m
function [sys,x0,str,ts,simStateCompliance] = ep7_3(t,x,u,flag)(2)修改子函数。
sizes.NumDiscStates = 1;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
x0 = 0;
ts = [0.5 0];%采样时间为0.5s
(3)对mdlUpdate和mdlOutputs子函数做修改。
function sys=mdlUpdate(t,x,u)
sys = u;
function sys=mdlOutputs(t,x,u)
sys = x;
(4)保存文件,搭建系统模型。
例7-4 用S-function实现下面离散系统。
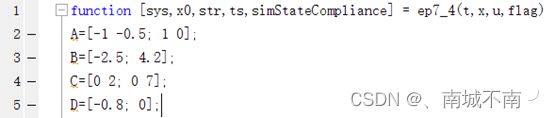
1、将模板sfuntmpl.m另存为ep7_4.m,并修改主函数名为ep7_4,并在主函数主体中输入矩阵A,B,C,D的值。
function [sys,x0,str,ts,simStateCompliance] = ep7_4(t,x,u,flag)
A=[-1 -0.5; 1 0];
B=[-2.5; 4.2];
C=[0 2; 0 7];
D=[-0.8; 0];
2、状态的更新和输出依赖于参数A,B,C,D,因此需要对mdlUpdate和mdlOutputs的调用做修改。
3、从A,B,C,D的维数中可以看出状态变量个数为2,输出变量个数为2,输入变量个数为1,修改mdlInitializeSizes初始化回调子函数。
4、修改和子函数,以满足对离散状态方程的实现:
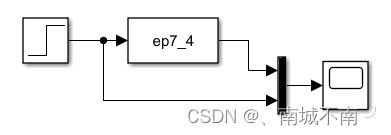
5、保存文件,搭建系统模型并运行。
3.用S-function实现连续系统。
首先对mdlInitializeSizes子函数进行修改,包括确定连续状态的个数、状态初始值、采样时间设置。另外,还要编写mdlDerivatives子函数,将状态的导数向量通过sys变量返回。
如果系统状态不止一个,可以通过索引x(1)、x(2)等得到各个状态。修改后的mdlOutputs中应该包含系统的输出方程。
例7-5 用S-function实现一个积分器。
对于一个积分器,输入与输出之间的关系为
(1)将模板sfuntmpl.m另存为ep7_5,并修改主函数名为ep7_5。
![]()
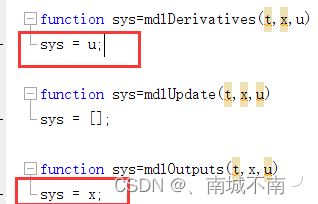
(2)修改mdlInitializeSizes子函数:
(3)对mdlDerivatives和mdlOutputs子函数做修改:
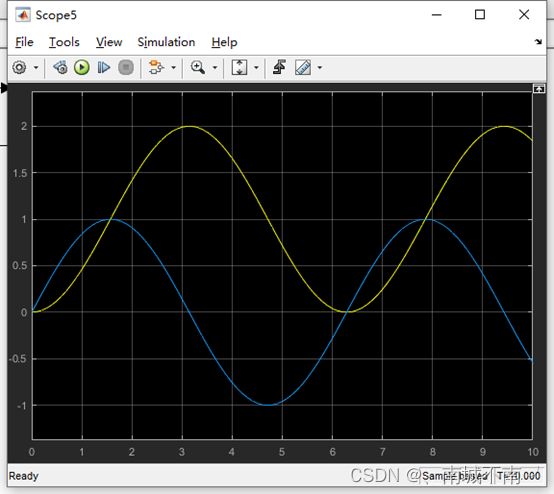
(4)保存文件,运行。
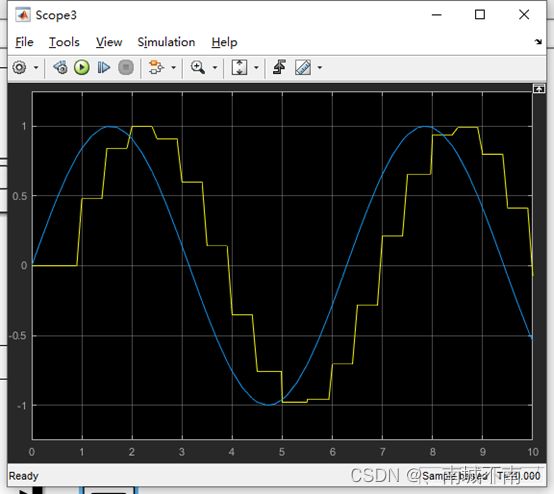
蓝线为正弦信号,黄线为积分后的1-cos(t)。
例7-6 用S-function实现下面的连续系统。
为了增强S-function模块的实用性,现要求系数矩阵A、B、C、D以及系统状态的初始值均可在参数对话框中设计。
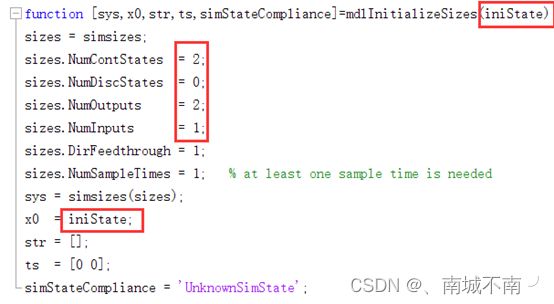
(1)将模板sfuntmpl.m另存为至ep7_6,并修改主函数名为ep7_6,添加参数A、B、C、D以及iniState。
function [sys,x0,str,ts,simStateCompliance] = ep7_6(t,x,u,flag,A,B,C,D,iniState)(2)调用初始化子函数时将参数iniState传递至mdlInitializeSizes子函数,状态导数和输出依赖于参数A,B,C,D以及iniState,因此需要对mdlInitializeSizes、mdlUpdate和mdlOutputs的调用做修改。
(3)修改mdlInitializeSizes初始化回调函数:
其中,初始值x0设为iniState,表示由外部设定。
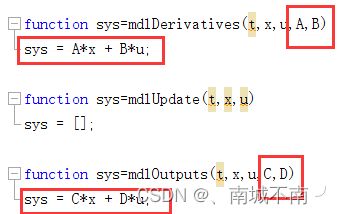
(4)对mdlUpdate和mdlOutputs子函数做修改:
(5)保存文件,搭建系统模型,并仿真。
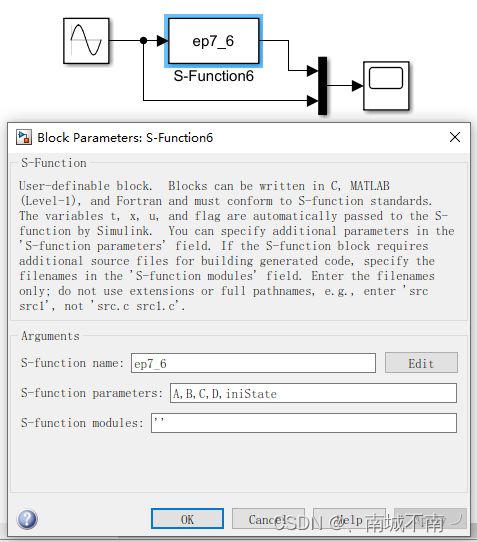
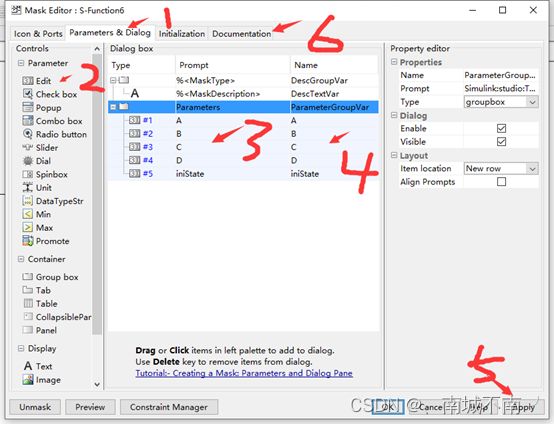
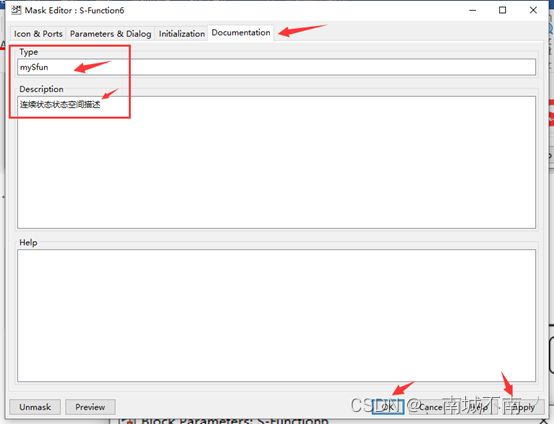
(6)对S-function模块进行封装。选择——菜单命令Diagrm——Mask——Create Mask,并编辑封装编辑器中的Parameters选项卡和Documentation选项卡。
(7)双击S-function,设置参数。
(8)运行系统仿真。
4、用S-function实现混合系统。
混合系统:既包含离散状态,又包含连续状态的系统。
例7-7 用S-function实现固定步长的混合系统。
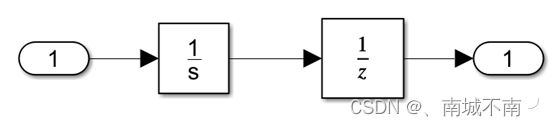
利用simulink自带的一个例子mixedm.m来说明如何实现,其作用相当于一个连续积分系统与一个离散单位延迟串联的系统。
(1)命令行:edit mixedm
(2)主函数部分:
dperiod = 1;
doffset = 0;%设置离散采样周期和偏移量。
switch flag % Initialization %
case 0
[sys,x0,str,ts]=mdlInitializeSizes(dperiod,doffset); % Derivatives %
%向初始化子函数传递离散采样周期和偏移量
case 1
sys=mdlDerivatives(t,x,u); % Update %
case 2,
sys=mdlUpdate(t,x,u,dperiod,doffset); % Output %
%向mdlUpdate状态更新子函数传递离散采样周期和偏移量
case 3
sys=mdlOutputs(t,x,u,doffset,dperiod);% Terminate %
%mdlOutputs输出子函数传递离散采样周期和偏移量
case 9 %case{4,9}
sys = []; % do nothing
%flag为4,因为是固定步长,所以不需要mdlGetTimeOfNextVarHit子函数
%flag为9,即simulink终止时,这里无特殊任务,所以也不需要
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
(3)初始化mdlInitializeSizes子函数
sizes = simsizes;
sizes.NumContStates = 1;%连续状态个数为1
sizes.NumDiscStates = 1;%离散状态个数为1
sizes.NumOutputs = 1;%输出个数为1
sizes.NumInputs = 1;%输入个数为1
sizes.DirFeedthrough = 0;%没有前馈
sizes.NumSampleTimes = 2;%两个采样时间
sys = simsizes(sizes);
x0 = ones(2,1);
str = [];
ts = [0 0; %一个采样时间是[0 0]表示连续系统% sample time
dperiod doffset]; %离散系统的采样时间
(4)mdlDerivatives、mdlUpdate、mdlOutputs子函数:
function sys=mdlDerivatives(t,x,u)
sys = u; %连续系统是一积分环节
% end mdlDerivatives
% mdlUpdate
% Handle discrete state updates, sample time hits, and major time step
% requirements.
function sys=mdlUpdate(t,x,u,dperiod,doffset)
% next discrete state is output of the integrator
if abs(round((t - doffset)/dperiod) - (t - doffset)/dperiod) < 1e-8
%如果仿真时间在采样点的正负1e-8范围内,更新状态,否则保持不变。
sys = x(1); %离散系统是一延迟环节
else
sys = [];
end
% end mdlUpdate
% mdlOutputs
% Return the output vector for the S-function
function sys=mdlOutputs(t,x,u,doffset,dperiod)
% Return output of the unit delay if we have a
% sample hit within a tolerance of 1e-8. If we
% don't have a sample hit then return [] indicating
% that the output shouldn't change.
if abs(round((t - doffset)/dperiod) - (t - doffset)/dperiod) < 1e-8
%如果仿真时间在采样点的正负1e-8范围内,输出,否则保持不变。
sys = x(2); %输出采样时间
else
sys = [];
end
% end mdlOutputs
(5)建立系统模型,并运行仿真。
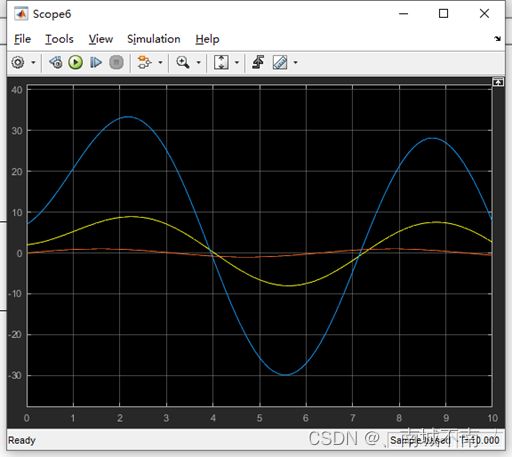
结论:蓝线为正弦信号,黄线为输出信号,可以看出正弦信号积分后,在经单位延迟离散采样的结果。
例7-8 用S-function实现变步长的混合系统。
自带例子vsfunc.m,其作用相当于下面系统:
其中,u(2)表示输入u的第二个分量,ut表示时刻t输入u的值,y_t+dt表示时刻t+dt输出y的值。
(1)命令行:edit vsfunc
(2)主函数部分,因为要执行mdlGetTimeOfNextVarHit子函数,所以flag为4时要调用该函数:
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u); % Terminate %
(3)mdlInitializeSizes初始化子函数
sizes.NumContStates = 0;
sizes.NumDiscStates = 1;%离散状态个数为1
sizes.NumOutputs = 1;%输出个数为1
sizes.NumInputs = 2;%输出个数为2
sizes.DirFeedthrough = 1;%有前馈
ts = [-2 0]; %变步长采样时间 % variable sample time
(4)其他子函数:
function sys=mdlUpdate(t,x,u)
sys = u(1);
function sys=mdlOutputs(t,x,u)
sys = x(1);
function sys=mdlGetTimeOfNextVarHit(t,x,u)
sys = t + u(2); %时间步长变化
结论:变步长系统的实现关键在于对采样时间ts和子函数mdlGetTimeOfNextVarHit的设置。
5、simulink自带S-function实例。
目录marlabroot\simulink\blocks下包含了许多M文件S-function。
命令行:sfundemos (查看相关实例)
或者在Simulink\User-Defined Functions模块库中打开。