MATLAB模糊控制器

        说明：以下例子均来自此书——《MATLAB/Simulink系统仿真超级学习手册》石良臣 matlab2018a ，仅作为读书笔记。

1、

2、

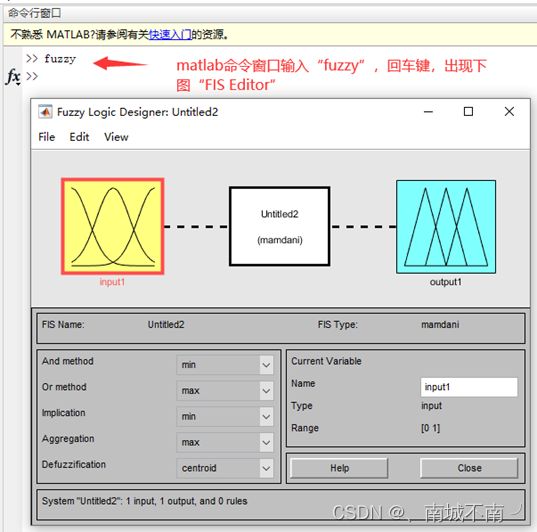
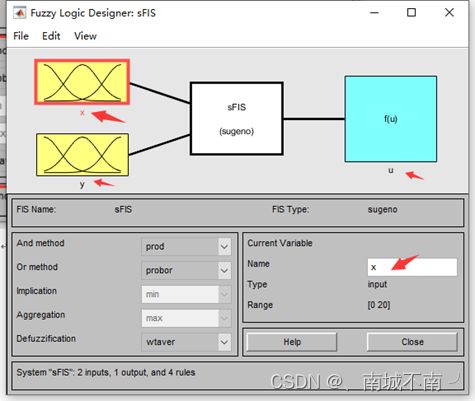
系统结构显示区：显示系统的输入输出个数以及模糊规则条数。

模糊逻辑区：显示并可编辑模糊逻辑预算、模糊推理、聚合和反模糊化方法。

3、菜单栏

 4、

 

 5、编辑FIS的维数。

6、编辑FIS输入输出变量的名称

 

 7、编辑FIS的名称

方法一：File——Export——To Workspace ，（暂时将FIS保存于工作空间，在命名）。

方法二：File——Export——To File，（将FIS保存至文件，这种方式不易丢失数据）。

 8、编辑模糊逻辑推理的具体算法。

（1）Mamdani型

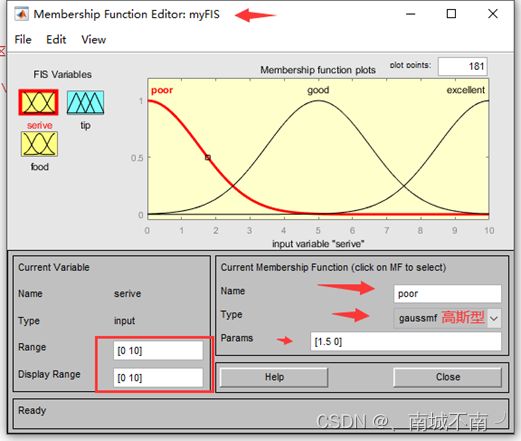
 二、隶属函数编辑器

1、MF编辑器界面介绍

 

 2、Mamdani型MF编辑

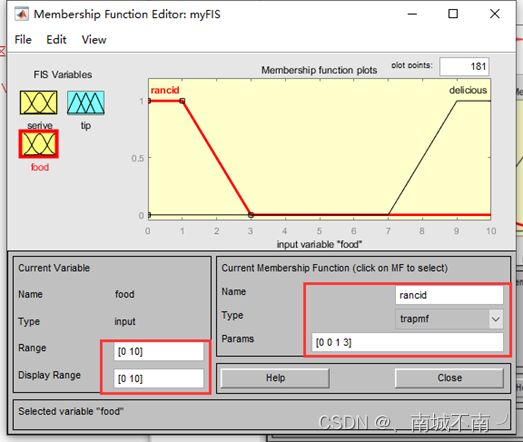
（1）编辑输入变量的论域和显示范围

（2）增加覆盖输入变量模糊子集的数目

方法一：Edit——Add MFs，

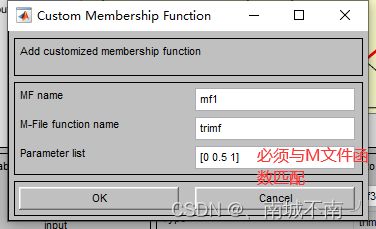
 方法二：Edit——Add Custom MF

 （3）编辑隶属函数曲线

（4）删除模糊子集

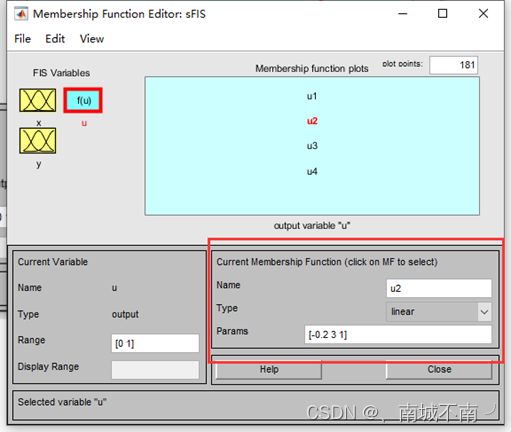
3、Sugeno型MF的编辑

不同：Mamdani型输出的是模糊子集；Sugeno型输出的是线性函数。

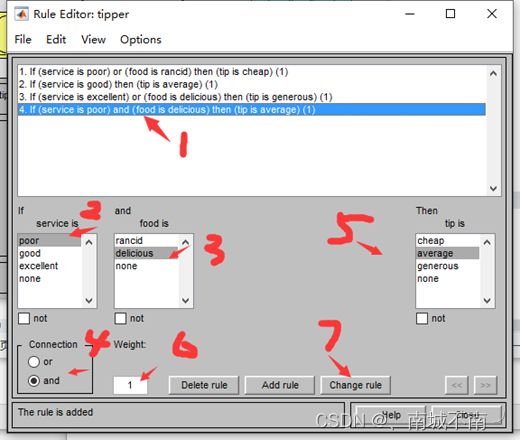
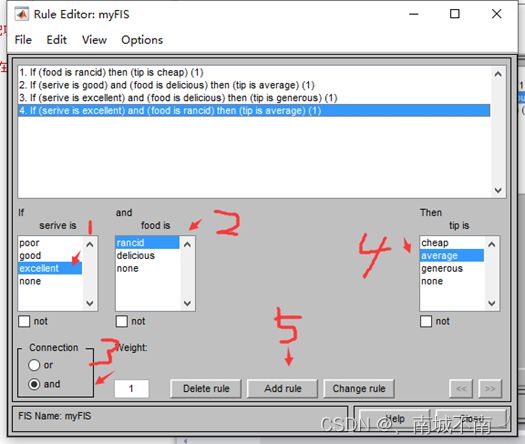
三、模糊规则编辑器

模糊规则就是输入变量和输出变量之间的模糊蕴含关系，编辑模糊规则之前

，必须先完成模糊系统的结构、模糊推理的类型和输入变量的模糊化编辑。

1、Rule编辑器界面简介

 

 

 

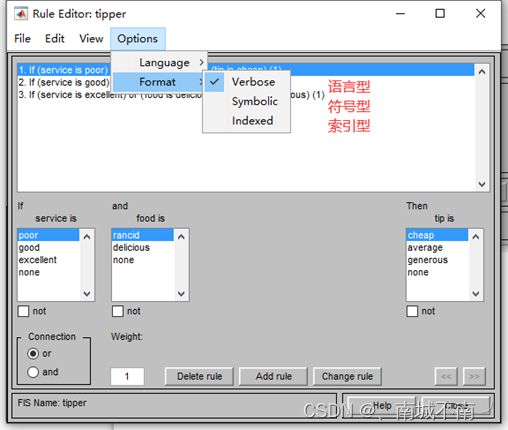
 2、模糊规则的格式

（1）语言型

每行末尾必须写上（p），p在区间[0,1]上，表示该条规则的权重。

例如：

 （2）符号型

例如：

 （3）索引型

 3、模糊规则的编辑

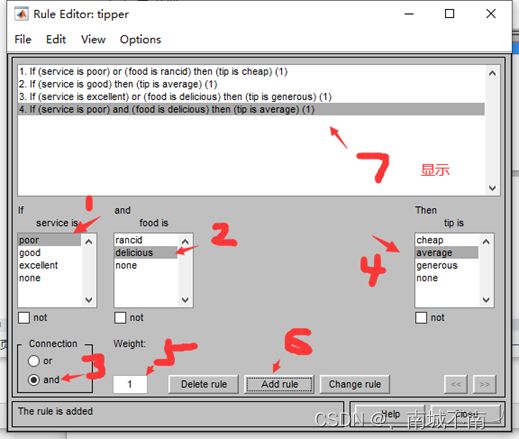
（1）添加模糊规则

（2）修改模糊规则

 （3）删除模糊规则

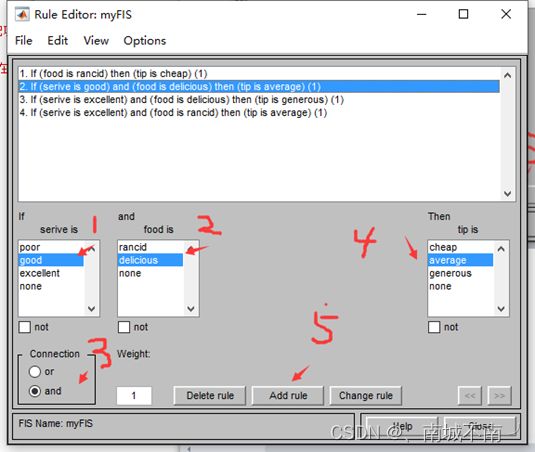
例题11-1

规律：

如果食物难吃，则小费很少；

如果餐厅服务一般但食物好吃，则小费比较接近平均；

如果餐厅服务很好而食物好吃，则小费会很多；

如果餐厅服务很好而食物难吃，则小费比较接近平均。

创建过程：

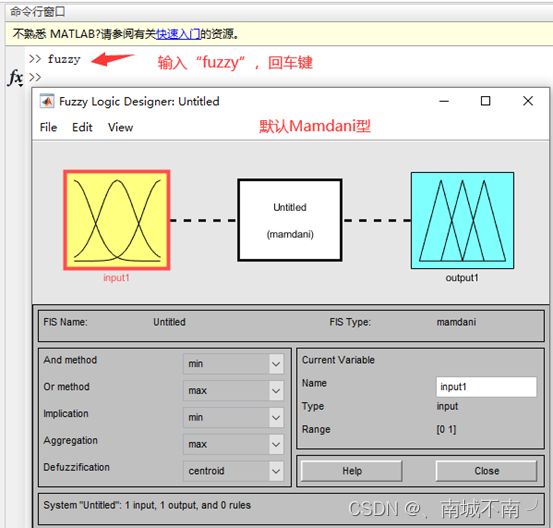
        （1）创建一个新的模糊推理系统

在MATLLAB命令窗口中输入fuzzy，按回车键确认。

 

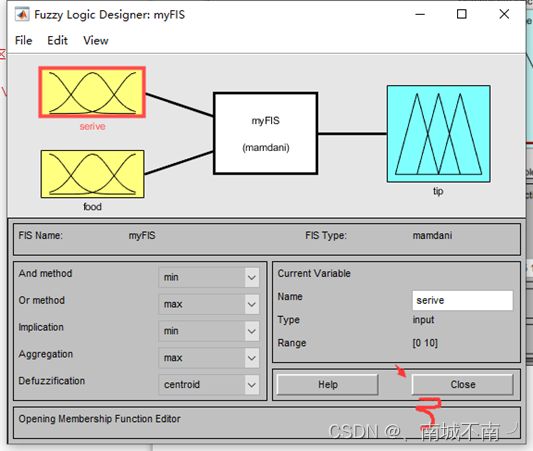
         （2）确定模糊推理系统的结构（默认Mamdani）

（三个都修改名称）

 （3）编辑模糊逻辑推理的具体算法（一般默认）

 

 （4）编辑输入、输出变量

 

 

 （5）编辑模糊规则

 

 

 

 （6）退出并保存模糊推理系统

 

 

 

 完成。

 四、模糊规则观察器

任意编辑器窗口“view”打开。

 

 五、曲面观察器

任意编辑器窗口“view”打开。

 当输入变量多余两个时，只能把两个之外的变量取成定值，显示在Ref,Input参量输入右侧的编辑框内，也可以在此编辑框内设置其他变量的取值。

例11-2

利用命令“fuzzy tipper”输出MATLAB自带图像，打开输出变量曲线观察器，分别研究每个输入变量对输出变量的影响。

解：

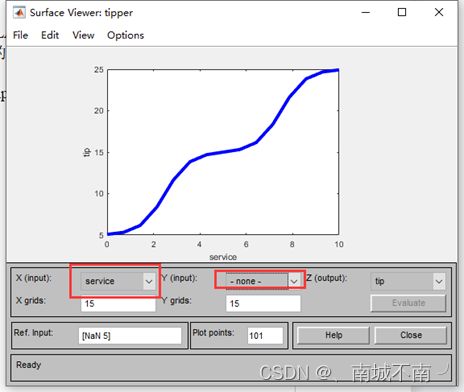
（1）输入变量service对输出变量tip的影响

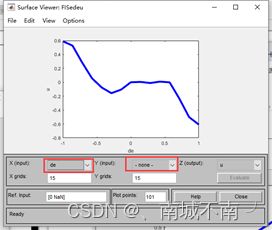
在X（input）编辑框内选择service，在Y（input）编辑框内选择-none-，就可以得到tip关于service的关系曲线：

 

（2）输入变量food对输出变量tip的影响

在X（input）编辑框内选择food，在Y（input）编辑框内选择-none-，就可以得到tip关于food的关系曲线：

六、模糊系统设计实例

当一个系统的内部结构不清楚，无法建立其数学模型时，如果它具有局部线性的特点并能进行分段描述，就可以用Sugeno型模糊进行描述。

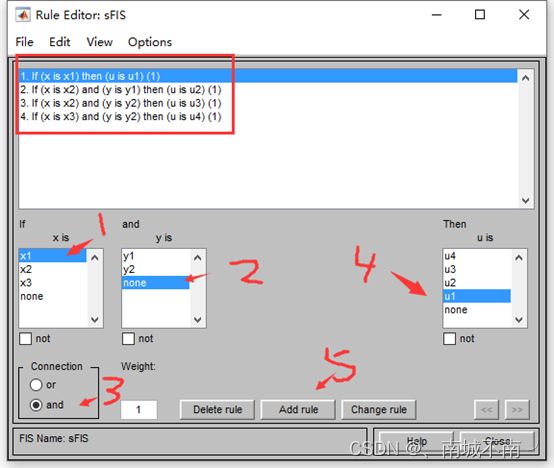
例：11-3一个系统，其输入为x和y，输出为u，根据大量的输入、输出数据，分析得出了四条模糊规则：

Rule: if x is x1 then u=u1=x+0.5;

Rule: if x is x2 and y is y1 then u=u2=-0.2x+3y+1;

Rule: if x is x2 and y is y2 then u=u3=0.3x+0.4y+5;

Rule: if x is x3 and y is y3 then u=u4=0.7x+0.1y-0.6;

输入变量x∈[0，20]，y∈[-5，15]，x1,x2,x3为涵盖输入变量x论域的模糊子集，y1,y2为涵盖输入变量y论域的模糊子集。

解：

（1）创建一个新的模糊推理系统

 （2）确定模糊系统的结构

 （3）编辑模糊逻辑推理的具体算法

 

 （4）编辑输入、输出变量

 双击输入输出变量x1

X2

 

X3

 Y1

 

Y2

 U1

 U2

 U3

 U4

 （5）编辑模糊规则

（6）观察模糊推理过程

由于本例中没有用到OR或方法，所以它对输出结果没有影响。而另外两个模糊逻辑推理算法的不同会导致输出结果大不相同。

（7）观察整个论域上输出变量与输入变量之间的关系

 

 

 七、11.4模糊控制系统仿真

1、MATLAB函数

（1）打开模糊推理系统GUI的函数

（2）对FIS进行操作的函数

2、FIS与模糊逻辑控制器连接

（1）把FIS导入工作空间

如：sFIS=readfis(‘sFIS’)

如：readfis——回车——选中文件。

如：

 （2）将FIS嵌入模糊控制器模块

 

3、模糊控制系统仿真的基本步骤：

（1）创建FIS文件；

（2）建立FIS文件与模糊控制器的连接；

（3）构建模糊控制系统的仿真模型；

（4）进行系统仿真。

八、构建模糊控制系统仿真模型的方法，并对仿真模型进行仿真。

例11-4一智能仿生人工腿中的执行电机传递函数可表示为

G(s)=6068s(s2+110s+6068)

试建立其闭环系统，并比较PID控制器与模糊控制器对闭环系统的控制性能。

解：

1、建立模糊逻辑控制系统

（1）在MATLAB命令窗口中输入fuzzy，创建一个新的FIS（Mamdani型）。

（2）编辑输入、输出变量

以闭环系统误差e及其de为两个输入变量，被控对象的控制输入u为输出变量。考虑到控制目标为跟踪单位阶跃信号，则e的论域为[-1，1]，de的论域为[-1，1]。同时为了满足控制输入的上界限制，取u的论域为[-2，2].。

 

 

 （3）制定、编辑模糊规则

当误差e为NB负大时，无论误差率de如何，控制输入都应该为NB负大，以尽快减小误差。

所以有规则Rule1： if e is NB then u is NB。

当误差e为NS负小时，就要考虑误差率的影响。如果de为NB负大，会导致e更负，所以控制输入仍然应该为NB负大；如果de为ZE零或PS正小，则需要较小的控制输入以帮助误差e恢复至零；如果de为PB正大，则不怎么需要控制输入。所以有下面的规则。

Rule2：if e is NS and de is NB then u is NB。

Rule3：if e is NS and de is NS then u is NB。

Rule4：if e is NS and de is ZE then u is NS。

Rule5：if e is NS and de is PS then u is NS。

Rule6：if e is NS and de is PB then u is ZE。

当误差e接近于零，即为ZE时，主要矛盾集中于稳定性，这时较小的控制输入会更加适合小幅度的调整，所以有下面的规则。

Rule7：if e is ZE and de is NB then u is PS。

Rule8：if e is ZE and de is NS then u is ZE。

Rule9：if e is ZE and de is ZE then u is ZE。

Rule10：if e is ZE and de is PS then u is ZE。

Rulell：if e is ZE and de is PB then u is NS。

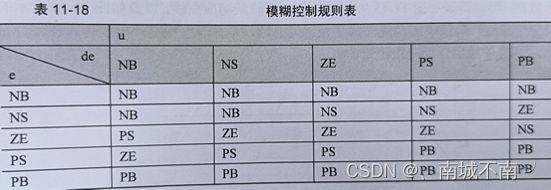
对称地可以得出余下的6条规则，表11-18为模糊控制规则表。

 

 （4）导入工作空间

 （5）建立仿真模型

 

 运行仿真，阶跃响应曲线非常平稳，没有超调量，没有振荡，效果比较好。

 2、利用PID控制器建立仿真模型

 

          根据Ziegler-Nichols调参方法，可以确定出一组PID参数：P=66、I=66/0.0403、D=66*0.0101、N=100，这组参数使得闭环系统稳定。

        运行仿真，虽然系统较快地趋于稳定，但产生了多次振荡，超调量很大，且控制输入也较大，不合符实际需求。

 3、对被控对象加入随机干扰，再次建立模糊逻辑控制系统。

 

        运行仿真，由于随机扰动的加入，响应曲线会一直处于波动状态，但基本稳定在1附近，这说明模糊逻辑控制器有一定的干扰抑制作用。

 4、Rule观察器

 

 5、Surface观察器

 

 八、MATLAB自带模糊控制系统实例

 

（结构文件列表）核心：tank=readfis(‘tank’)

        FIS由五个部分组成，即FIS编辑器、隶属函数编辑器、模糊规则编辑器、模糊规则观察器、曲面观察器。