轮胎特性图绘制
参考文献《基于“魔术公式”的轮胎动力学仿真分析》。
1、 不同垂直载荷Fz的纵向力Fx图
(1)搭建simulink模型。
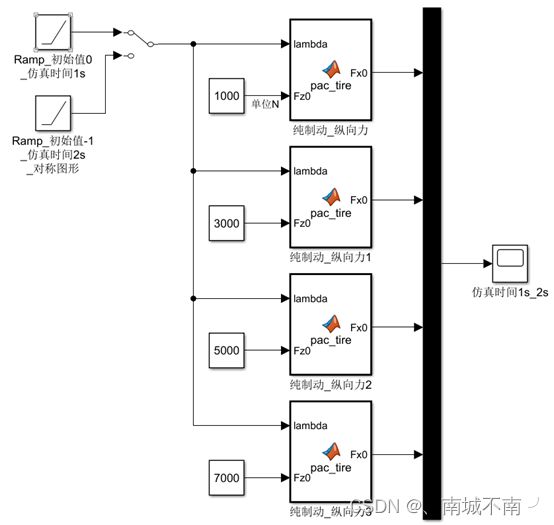
(2)在matlab function 模块中创建魔术公式轮胎。
function Fx0 = pac_tire(lambda,Fz0)
%魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
% gamma = 0;%外倾角为0。
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
Fz=Fz0/1000;%单位:kN。
%% 纵向力Fx
a0=1.65;
a1=-21.3;
a2=1144;
a3=49.6;
a4=226;
a5=0.069;
a6=-0.006;
a7=0.056;
a8=0.486;
%% 参数Fx
Cx=a0;%曲线形状因子
Dx=(a1*Fz^2+a2*Fz);%峰值因子(曲线的最大值)
BCDx=(a3*Fz^2+a4*Fz)*exp(-a5*Fz);
Bx=BCDx/(Cx*Dx);%刚度因子
Ex=a6*Fz^2+a7*Fz+a8;%曲线曲率因子(曲线最大值附近的形状)
% Shx=a9*Fz+a10;%曲线的水平方向漂移
Shx=0;
Svx=0;%曲线的垂直方向漂移
X=(lambda*100+Shx);%此处lambda*100;lambda∈【0,1】。
% Fx0=(a1*Fz^2+a2*Fz)*sin(a0*atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-(a6*Fz^2+a7*Fz+a8)*(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))))));
Fx0=Dx*sin(Cx*atan(Bx*X-Ex*(Bx*X-atan(Bx*X)))) + Svx;
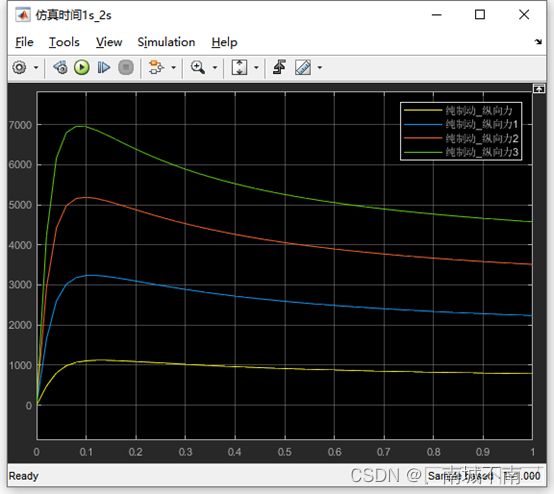
(3)仿真工况一:Ramp模块的初始值设置为0,仿真时间设置为1s。
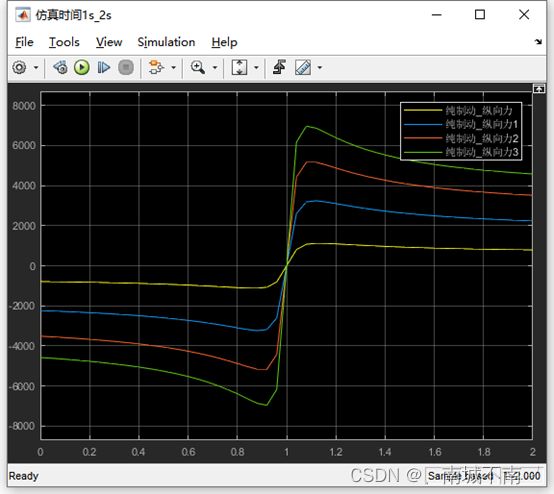
仿真工况二:Ramp模块的初始值设置为-1,仿真时间设置为2s。
2、 不同垂直载荷Fz的侧向力Fy图。
(1)搭建simulink模型。
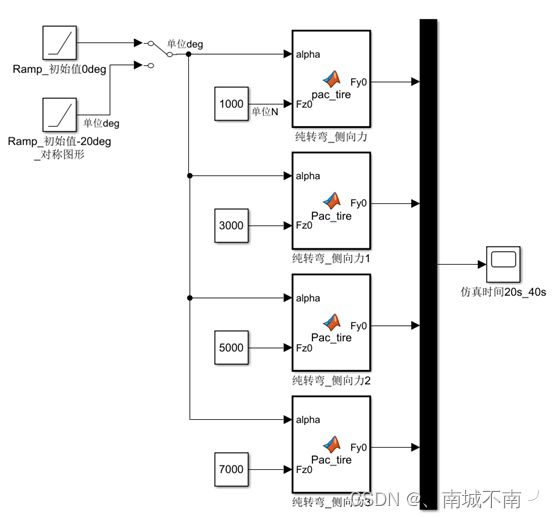
(2)在matlab function 模块中创建魔术公式轮胎。
function Fy0 = pac_tire(alpha,Fz0)
%魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
gamma = 0;%外倾角为0。
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
Fz=Fz0/1000;%单位:kN。
%% 稳态纯转向工况下侧向力Fy0
%拟合参数Fy0
b0=1.3;
b1=-22.1;
b2=1011;
b3=1078;
b4=1.82;
b5=0.208;
b6=0;
b7=-0.354;
b8=0.707;
b9=0.028;
b10=0;
b11=14.8;
b12=0.022;
%% 参数Fy0
Cy=b0;
Dy=(b1*Fz^2+b2*Fz);
%有点不一样
BCDy=b3*sin(b4*atan(b5*Fz))*(1-b12*abs(gamma));%gamma为外倾角。
By=BCDy/(Cy*Dy);
Ey=b6*Fz^2+b7*Fz+b8;
Shy=b9*gamma;
Svy=(b10*Fz^2+b11*Fz)*gamma;
%
Y=alpha+Shy;%侧偏角alpha_y
%Fy0——正的测偏角,负的侧偏力。
Fy0=-Dy*sin(Cy*atan(By*Y-Ey*(By*Y-atan(By*Y)))) + Svy;
(3)仿真工况一:Ramp模块的初始值设置为0deg,仿真时间设置为20s。

仿真工况二:Ramp模块的初始值设置为20deg,仿真时间设置为40s。
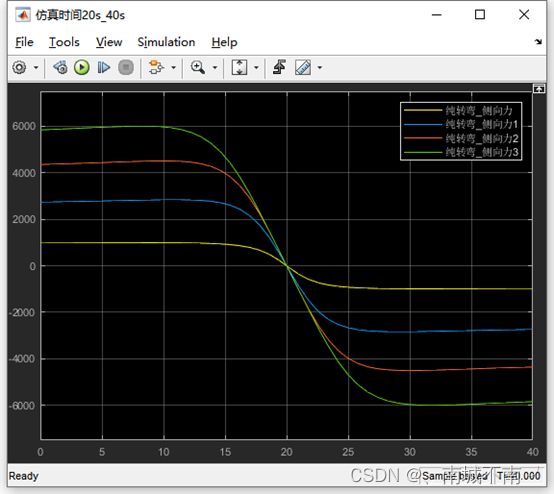
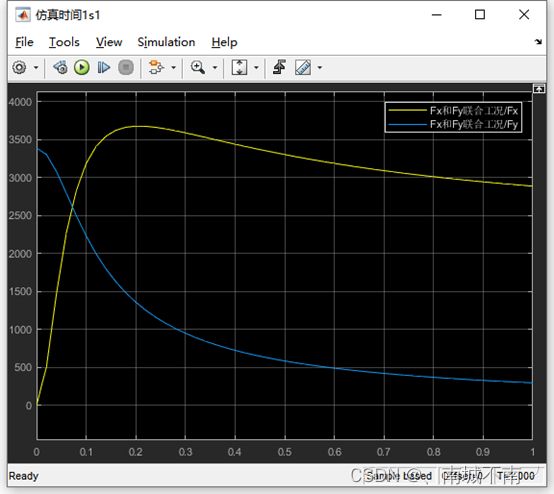
3、侧偏角为5°时,纵向力Fx和侧向力Fy,随滑移率的变化曲线。
(1)搭建simulink模型。

(2)在matlab function 模块中创建魔术公式轮胎。
function [Fx,Fy] = pac_tire(lambda,alpha,Fz0)
%魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
gamma = 0;%外倾角为0。
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
% 纵向力中的lambda=lambda*100;%滑移率【0%,100%】。
Fz=Fz0/1000;%单位:kN。
%% 纵向力Fx
a0=1.65;
a1=-21.3;
a2=1144;
a3=49.6;
a4=226;
a5=0.069;
a6=-0.006;
a7=0.056;
a8=0.486;
%% 参数Fx
Cx=a0;%曲线形状因子
Dx=(a1*Fz^2+a2*Fz);%峰值因子(曲线的最大值)
BCDx=(a3*Fz^2+a4*Fz)*exp(-a5*Fz);
Bx=BCDx/(Cx*Dx);%刚度因子
Ex=a6*Fz^2+a7*Fz+a8;%曲线曲率因子(曲线最大值附近的形状)
Shx=0;%曲线的水平方向漂移
Svx=0;%曲线的垂直方向漂移
X=(lambda*100+Shx);%此处lambda*100;lambda∈【0,1】。
% Fx0=(a1*Fz^2+a2*Fz)*sin(a0*atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-(a6*Fz^2+a7*Fz+a8)*(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))))));
Fx0=Dx*sin(Cx*atan(Bx*X-Ex*(Bx*X-atan(Bx*X)))) + Svx;
%% %魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
% 侧偏力中的alpha=alpha*180/pi;%单位换算rad_to_deg。
%% 稳态纯转向工况下侧向力Fy0
%拟合参数Fy0
b0=1.3;
b1=-22.1;
b2=1011;
b3=1078;
b4=1.82;
b5=0.208;
b6=0;
b7=-0.354;
b8=0.707;
b9=0.028;
b10=0;
b11=14.8;
b12=0.022;
%% 参数Fy0
Cy=b0;
Dy=(b1*Fz^2+b2*Fz);
BCDy=b3*sin(b4*atan(b5*Fz))*(1-b12*abs(gamma));%gamma为外倾角。
By=BCDy/(Cy*Dy);
Ey=b6*Fz^2+b7*Fz+b8;
Shy=b9*gamma;
Svy=(b10*Fz^2+b11*Fz)*gamma;
Y=alpha+Shy;%侧偏角alpha_y
%% %Fy0——正的测偏角(deg),负的侧偏力。
Fy0=-Dy*sin(Cy*atan(By*Y-Ey*(By*Y-atan(By*Y)))) + Svy;
%% %联合仿真工况
sigma_x=lambda/(1+abs(lambda));%此处lambda输入【0,1】。
sigma_y=tan(alpha*pi/180)/(1+abs(lambda));%此处alpha的单位为rad。
sigma=sqrt(sigma_x^2+sigma_y^2);
Fx=sign(lambda)*Fx0*sigma_x/sigma;
Fy=sign(alpha)*Fy0*sigma_y/sigma;
% %联合仿真工况
% sigma_x=-lambda/(1+abs(lambda));%此处lambda输入【0,1】。
% sigma_y=-tan(alpha*pi/180)/(1+abs(lambda));%此处alpha的单位为rad。
% sigma=sqrt(sigma_x^2+sigma_y^2);
% Fx=Fx0*sigma_x/sigma;
% Fy=Fy0*sigma_y/sigma;
(3)仿真工况:Ramp模块的初始值设置为0,仿真时间设置为1s。
4、载荷4kN,外倾角为0,不同侧偏角。
(1)搭建simulink模型。

(2)在matlab function 模块中创建魔术公式轮胎。
function [Fx,Fy] = pac_tire(lambda,alpha,Fz0)
%魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
gamma = 0;%外倾角为0。
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
% 纵向力中的lambda=lambda*100;%滑移率【0%,100%】。
Fz=Fz0/1000;%单位:kN。
%% 纵向力Fx
a0=1.65;
a1=-21.3;
a2=1144;
a3=49.6;
a4=226;
a5=0.069;
a6=-0.006;
a7=0.056;
a8=0.486;
%% 参数Fx
Cx=a0;%曲线形状因子
Dx=(a1*Fz^2+a2*Fz);%峰值因子(曲线的最大值)
BCDx=(a3*Fz^2+a4*Fz)*exp(-a5*Fz);
Bx=BCDx/(Cx*Dx);%刚度因子
Ex=a6*Fz^2+a7*Fz+a8;%曲线曲率因子(曲线最大值附近的形状)
Shx=0;%曲线的水平方向漂移
Svx=0;%曲线的垂直方向漂移
X=(lambda*100+Shx);%此处lambda*100;lambda∈【0,1】。
% Fx0=(a1*Fz^2+a2*Fz)*sin(a0*atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-(a6*Fz^2+a7*Fz+a8)*(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))))));
Fx0=Dx*sin(Cx*atan(Bx*X-Ex*(Bx*X-atan(Bx*X)))) + Svx;
%% %魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
% 侧偏力中的alpha=alpha*180/pi;%单位换算rad_to_deg。
%% 稳态纯转向工况下侧向力Fy0
%拟合参数Fy0
b0=1.3;
b1=-22.1;
b2=1011;
b3=1078;
b4=1.82;
b5=0.208;
b6=0;
b7=-0.354;
b8=0.707;
b9=0.028;
b10=0;
b11=14.8;
b12=0.022;
%% 参数Fy0
Cy=b0;
Dy=(b1*Fz^2+b2*Fz);
BCDy=b3*sin(b4*atan(b5*Fz))*(1-b12*abs(gamma));%gamma为外倾角。
By=BCDy/(Cy*Dy);
Ey=b6*Fz^2+b7*Fz+b8;
Shy=b9*gamma;
Svy=(b10*Fz^2+b11*Fz)*gamma;
Y=alpha+Shy;%侧偏角alpha_y
%% %Fy0——正的测偏角(deg),负的侧偏力。
Fy0=-Dy*sin(Cy*atan(By*Y-Ey*(By*Y-atan(By*Y)))) + Svy;
%% %联合仿真工况
sigma_x=lambda/(1+abs(lambda));%此处lambda输入【0,1】。
sigma_y=tan(alpha*pi/180)/(1+abs(lambda));%此处alpha的单位为rad。
sigma=sqrt(sigma_x^2+sigma_y^2);
Fx=sign(lambda)*Fx0*sigma_x/sigma;
Fy=sign(alpha)*Fy0*sigma_y/sigma;
% %联合仿真工况
% sigma_x=-lambda/(1+abs(lambda));%此处lambda输入【0,1】。
% sigma_y=-tan(alpha*pi/180)/(1+abs(lambda));%此处alpha的单位为rad。
% sigma=sqrt(sigma_x^2+sigma_y^2);
% Fx=Fx0*sigma_x/sigma;
% Fy=Fy0*sigma_y/sigma;
(3)仿真工况一:Ramp模块的初始值设置为0deg,仿真时间设置为1s。
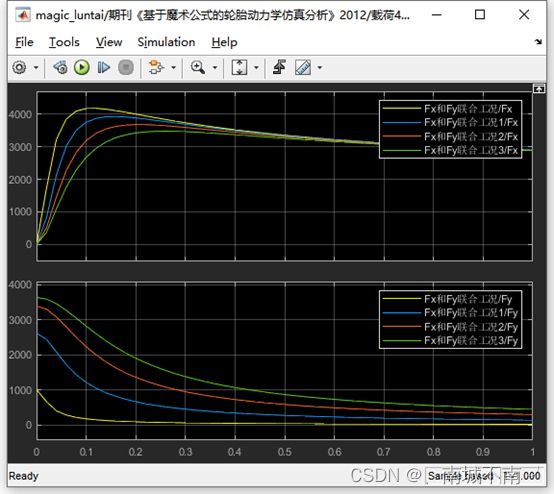
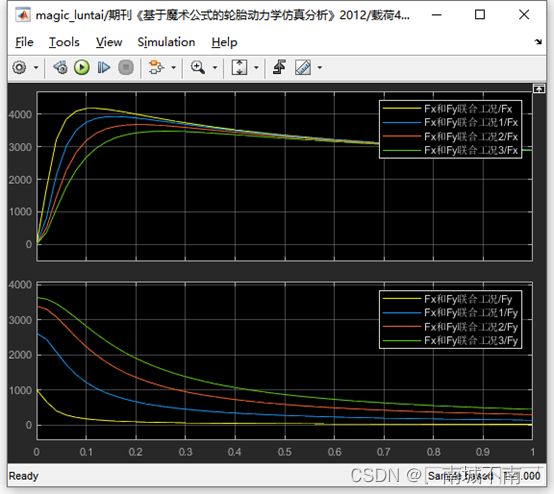
(4)在matlab中绘制附着椭圆图。
1)代码
%matlab绘图命令
clc
x1=Fx(:,1);
x2=Fx(:,2);
x3=Fx(:,3);
x4=Fx(:,4);
y1=Fy(:,1);
y2=Fy(:,2);
y3=Fy(:,3);
y4=Fy(:,4);
hold on
plot(x1,y1);
plot(x2,y2);
plot(x3,y3);
plot(x4,y4);
legend("1°","3°","5°","7°");
xlabel("纵向力Fx");
ylabel("侧向力Fy" );
2)附着椭圆
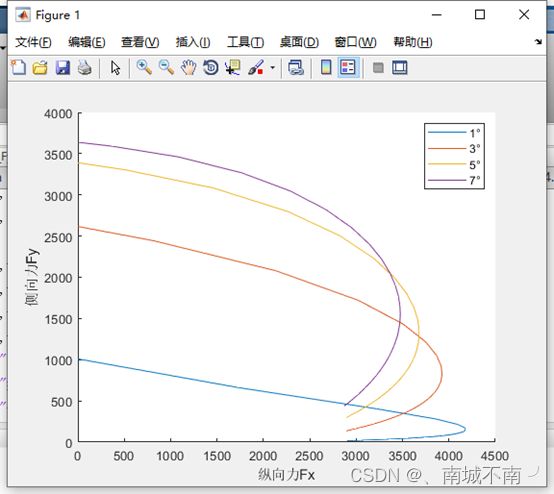
5、不同路面附着系数mu下的侧偏力曲线。
(1)搭建simulink模型。
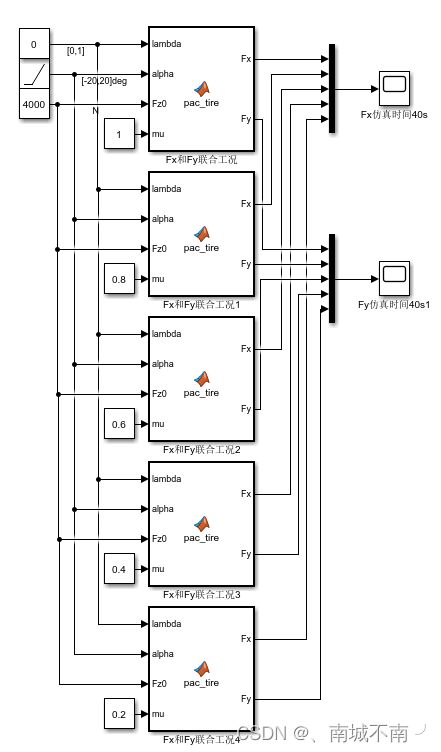
(2)在matlab function 模块中创建魔术公式轮胎。
function [Fx,Fy] = pac_tire(lambda,alpha,Fz0,mu)
%魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
gamma = 0;%外倾角为0。
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
% 纵向力中的lambda=lambda*100;%滑移率【0%,100%】。
Fz=Fz0/1000;%单位:kN。
%% 纵向力Fx
a0=1.65;
a1=-21.3;
a2=1144;
a3=49.6;
a4=226;
a5=0.069;
a6=-0.006;
a7=0.056;
a8=0.486;
%% 参数Fx
Cx=a0;%曲线形状因子
Dx=(a1*Fz^2+a2*Fz) * mu;%峰值因子(曲线的最大值)
BCDx=(a3*Fz^2+a4*Fz)*exp(-a5*Fz);
Bx=BCDx/(Cx*Dx);%刚度因子
Ex=a6*Fz^2+a7*Fz+a8;%曲线曲率因子(曲线最大值附近的形状)
Shx=0;%曲线的水平方向漂移
Svx=0;%曲线的垂直方向漂移
X=(lambda*100+Shx);%此处lambda*100;lambda∈【0,1】。
% Fx0=(a1*Fz^2+a2*Fz)*sin(a0*atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-(a6*Fz^2+a7*Fz+a8)*(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))-atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*(x+(a9*Fz+a10))))));
Fx0=Dx*sin(Cx*atan(Bx*X-Ex*(Bx*X-atan(Bx*X)))) + Svx;
%% %魔术轮胎公式——期刊《基于魔术公式的轮胎动力学仿真分析》2012
%不考虑车轮外倾角和漂移的影响,拟合出的以下参数(即gamma=0;Sh=Sv=0。)
% 侧偏力中的alpha=alpha*180/pi;%单位换算rad_to_deg。
%% 稳态纯转向工况下侧向力Fy0
%拟合参数Fy0
b0=1.3;
b1=-22.1;
b2=1011;
b3=1078;
b4=1.82;
b5=0.208;
b6=0;
b7=-0.354;
b8=0.707;
b9=0.028;
b10=0;
b11=14.8;
b12=0.022;
%% 参数Fy0
Cy=b0;
Dy=(b1*Fz^2+b2*Fz) * mu;
BCDy=b3*sin(b4*atan(b5*Fz))*(1-b12*abs(gamma));%gamma为外倾角。
By=BCDy/(Cy*Dy);
Ey=b6*Fz^2+b7*Fz+b8;
Shy=b9*gamma;
Svy=(b10*Fz^2+b11*Fz)*gamma;
Y=alpha+Shy;%侧偏角alpha_y
%% %Fy0——正的测偏角(deg),负的侧偏力。
Fy0=-Dy*sin(Cy*atan(By*Y-Ey*(By*Y-atan(By*Y)))) + Svy;
%% %联合仿真工况
sigma_x=lambda/(1+abs(lambda));%此处lambda输入【0,1】。
sigma_y=tan(alpha*pi/180)/(1+abs(lambda));%此处alpha的单位为rad。
sigma=sqrt(sigma_x^2+sigma_y^2);
Fx=sign(lambda)*Fx0*sigma_x/sigma;
Fy=sign(alpha)*Fy0*sigma_y/sigma;
(3)仿真工况一:Ramp模块的初始值设置为-20deg,仿真时间设置为40s。
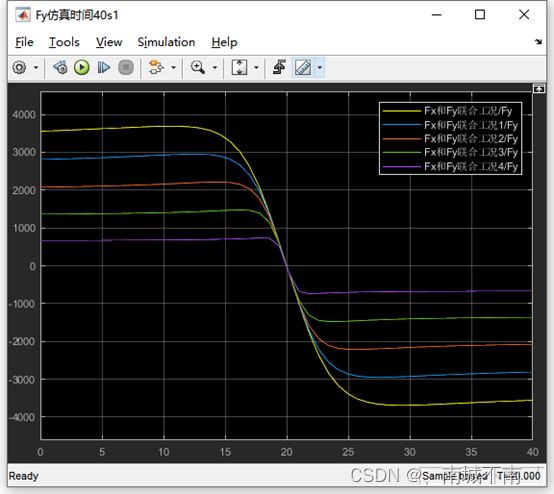
5、使用carsim软件中的轮胎参数表格绘制三维图。
将carsim中轮胎参数excel表格另存,表格重命名为“轮胎参数”。
![]()
轮胎参数excel表格中的数据命名如下:
![]()
%% 三维魔术轮胎曲线拟合
% y=d*sin(c*atan(b*x-e*(b*x-atan(b*x))));%魔术公式轮胎
%% 使用工具箱z=f(x,y)——Fx/Fy/Mz=(lambda/alpha,Fz);对应X——;Y——Fz;z——ZZ;
% y=(a1*y^2+a2*y)*y*sin(c*atan(b*x-e*(b*x-atan(b*x))));%曲线拟合公式
% % Fx0=(a1*Fz^2+a2*Fz)*sin(a0*atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*lambda*100-(a6*Fz^2+a7*Fz+a8)*(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*lambda*100-atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*lambda*100))));
% % Fy0=-(b1*Fz^2+b2*Fz)*sin(b0*atan((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*alpha-(b6*Fz^2+b7*Fz+b8)*((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*alpha-atan((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*alpha))));
% % Mz=(c1*Fz^2+c2*Fz)*sin(c0*atan(((c3*Fz^2+c4*Fz)*exp(-c5*Fz)/(c0*(c1*Fz^2+c2*Fz)))*alpha-(c6*Fz^2+c7*Fz+c8)*(((c3*Fz^2+c4*Fz)*exp(-c5*Fz)/(c0*(c1*Fz^2+c2*Fz)))*alpha-atan(((c3*Fz^2+c4*Fz)*exp(-c5*Fz)/(c0*(c1*Fz^2+c2*Fz)))*alpha))));
%% x——使用工具箱拟合参数
% % Fx0=(a1*Fz^2+a2*Fz)*sin(a0*atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*x*100-(a6*Fz^2+a7*Fz+a8)*(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*x*100-atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*x*100))));
% % Fy0=-(b1*Fz^2+b2*Fz)*sin(b0*atan((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*x-(b6*Fz^2+b7*Fz+b8)*((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*x-atan((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*x))));
% % Mz=(c1*Fz^2+c2*Fz)*sin(c0*atan(((c3*Fz^2+c4*Fz)*exp(-c5*Fz)/(c0*(c1*Fz^2+c2*Fz)))*x-(c6*Fz^2+c7*Fz+c8)*(((c3*Fz^2+c4*Fz)*exp(-c5*Fz)/(c0*(c1*Fz^2+c2*Fz)))*x-atan(((c3*Fz^2+c4*Fz)*exp(-c5*Fz)/(c0*(c1*Fz^2+c2*Fz)))*x))));
%% Excel表格数据由Carsim得到
clc;close all;clear
%% 轮胎纵向力Fx
lambda=xlsread("轮胎数据","Fx","A2:A52");%第一列
Fz1=xlsread("轮胎数据","Fx","B1:I1")/1000;%单位kN。%第一行
y11=xlsread("轮胎数据","Fx","B2:B52");%列%%y11-y81数据主要用于使用工具箱进行曲线拟合效果观察。
y21=xlsread("轮胎数据","Fx","C2:C52");
y31=xlsread("轮胎数据","Fx","D2:D52");
y41=xlsread("轮胎数据","Fx","E2:E52");
y51=xlsread("轮胎数据","Fx","F2:F52");%列
y61=xlsread("轮胎数据","Fx","G2:G52");
y71=xlsread("轮胎数据","Fx","H2:H52");
y81=xlsread("轮胎数据","Fx","I2:I52");
zz=xlsread("轮胎数据","Fx","B2:I52");%框选Fx\Fy\Mz的取值范围【左上角,右下角】
figure(1)
[x,y]=meshgrid(lambda,Fz1);%二维图%%%[x, y] = meshgrid(x,y);% 快速生成网格所需的数据
z=zz';%转置。
% subplot(1,2,1)
Fx=mesh(x,y,z);%%三维网格图mesh(x,y,z);%%x是n维向量,y是m维向量,z是m*n维向量
% subplot(1,2,2)
% surf(x,y,z) % (X(j), Y(i), Z(i,j))是线框网格线的交点
axis vis3d % 冻结屏幕高宽比,使得一个三维对象的旋转不会改变坐标轴的刻度显示
%% 标注x
xlabel("滑移率(S)");
ylabel("垂直载荷(Fz)");
zlabel("纵向力Fx");
%% 轮胎侧向力Fy
alpha=xlsread("轮胎数据","Fy","A2:A52");%第一列
Fz2=xlsread("轮胎数据","Fy","B1:I1")/1000;%单位kN。%第一行
y12=xlsread("轮胎数据","Fy","B2:B52");%列
y22=xlsread("轮胎数据","Fy","C2:C52");
y32=xlsread("轮胎数据","Fy","D2:D52");
y42=xlsread("轮胎数据","Fy","E2:E52");
y52=xlsread("轮胎数据","Fy","F2:F52");%列
y62=xlsread("轮胎数据","Fy","G2:G52");
y72=xlsread("轮胎数据","Fy","H2:H52");
y82=xlsread("轮胎数据","Fy","I2:I52");
zz2=xlsread("轮胎数据","Fy","B2:I52");%框选Fx\Fy\Mz的取值范围【左上角,右下角】
figure(2)
[x2,y2]=meshgrid(alpha,Fz2);%二维图
z2=zz2';%转置。
Fy=mesh(x2,y2,z2);%三维图
surf(x2,y2,z2) % (X(j), Y(i), Z(i,j))是线框网格线的交点
%% 标注y
xlabel("侧偏角alpha/(°)");
ylabel("垂直载荷Fz/(N)");
zlabel("侧偏力Fy/(N)");
%% 轮胎回正力矩
alpha=xlsread("轮胎数据","Mz","A2:A52");%第一列
Fz3=xlsread("轮胎数据","Mz","B1:I1")/1000;%单位kN。%第一行
y13=xlsread("轮胎数据","Mz","B2:B52");%列
y23=xlsread("轮胎数据","Mz","C2:C52");
y33=xlsread("轮胎数据","Mz","D2:D52");
y43=xlsread("轮胎数据","Mz","E2:E52");
y53=xlsread("轮胎数据","Mz","F2:F52");%列
y63=xlsread("轮胎数据","Mz","G2:G52");
y73=xlsread("轮胎数据","Mz","H2:H52");
y83=xlsread("轮胎数据","Mz","I2:I52");
zz3=xlsread("轮胎数据","Mz","B2:I52");%框选Fx\Fy\Mz的取值范围【左上角,右下角】
figure(3)
[x3,y3]=meshgrid(alpha,Fz3);%二维图
z3=zz3';%转置。
subplot(1,2,1)
Mz=mesh(x3,y3,z3);%三维网格图mesh(x,y,z)
subplot(1,2,2)
surf(x3,y3,z3) % (X(j), Y(i), Z(i,j))是线框网格线的交点
%% 标注z
xlabel("侧偏角alpha/(°)");
ylabel("垂直载荷Fz/(kN)");
zlabel("回正力矩Mz(N)");
%% 读取 Microsoft Excel 电子表格文件
%% num = xlsread(filename,sheet,xlRange)
%SSE为方差
%均方根植接近于1是最好的。
%% 标注
% xlabel("滑移率/侧偏角");
% ylabel("垂直载荷Fz");
% zlabel("纵向力Fx/侧偏力Fy/回正力矩Mz");
%% 魔术公式轮胎
%% Fx
% Cx=a0;%曲线形状因子
% Dx=(a1*Fz^2+a2*Fz);%峰值因子(曲线的最大值)
% BCDx=(a3*Fz^2+a4*Fz)*exp(-a5*Fz);
% Bx=BCDx/(Cx*Dx);%刚度因子
% Ex=(a6*Fz^2+a7*Fz+a8);%曲线曲率因子(曲线最大值附近的形状)
% X=lambda*100;%滑移率使用百分比。
% Fx0=Dx*sin(Cx*atan(Bx*X-Ex*(Bx*X-atan(Bx*X))));
% % Bx=((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)));
% % Fx0=(a1*Fz^2+a2*Fz)*sin(a0*atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*lambda*100-(a6*Fz^2+a7*Fz+a8)*(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*lambda*100-atan(((a3*Fz^2+a4*Fz)*exp(-a5*Fz)/(a0*(a1*Fz^2+a2*Fz)))*lambda*100))));
%% Fy——忽略外倾角。
% Cy=b0;
% Dy=(b1*Fz^2+b2*Fz);
% % BCDy=b3*sin(b4*atan(b5*Fz))*(1-b12*abs(gamma));%gamma为外倾角。
% BCDy=b3*sin(b4*atan(b5*Fz));
% By=BCDy/(Cy*Dy);
% Ey=(b6*Fz^2+b7*Fz+b8);
% Y=alpha;
% Fy0=-Dy*sin(Cy*atan(By*Y-Ey*(By*Y-atan(By*Y))));%Fy0——正的测偏角(deg),负的侧偏力。
% % By=(b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)));
% % Fy0=-(b1*Fz^2+b2*Fz)*sin(b0*atan((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*alpha-(b6*Fz^2+b7*Fz+b8)*((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*alpha-atan((b3*sin(b4*atan(b5*Fz))/(b0*(b1*Fz^2+b2*Fz)))*alpha))));
结束。


