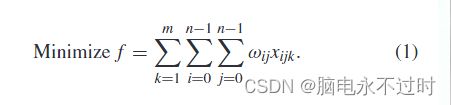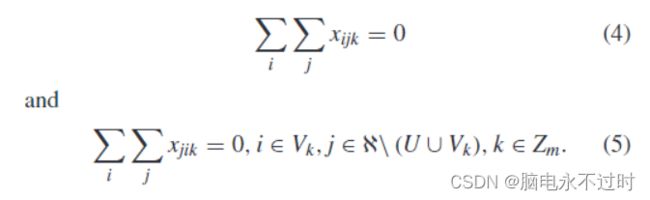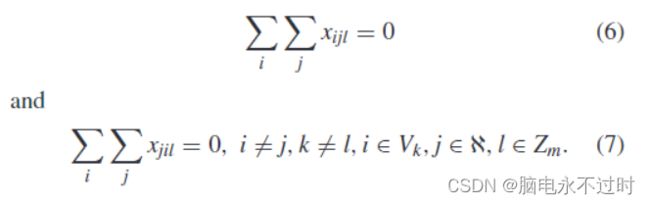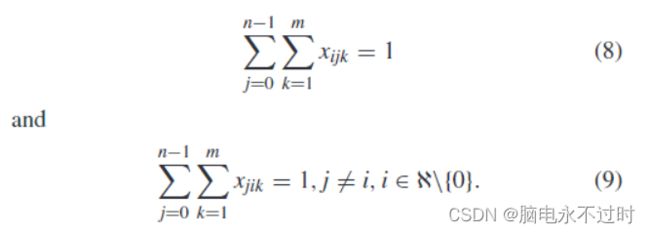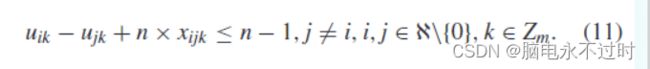颜色旅行商问题
英文：Colored Traveling Salesman Problem
摘要：
多旅行商问题是一个重要的组合优化问题。它已被广泛且成功地应用于多旅行商（销售人员）共享公共工作空间（城市集）的实际案例中。然而，它不能代表一些应用程序问题，即多个旅行商不仅有自己的专属任务，而且彼此共享一组任务。这项工作提出了一种新的MTSP，用于处理此类情况，被称为有色人种旅行推销员问题colored traveling salesman problem（CTSP）。定义了两种类型的城市组，即每组唯一颜色的专属城市供销售人员访问，以及一组多种颜色的共享城市供所有销售人员访问。有证据表明，CTSP是NP难的，多点MTSP和多个单个旅行推销员问题是其特例。我们提出了一种用于CTSP的双染色体编码遗传算法，并分析了相应的解空间。然后，通过结合贪婪、爬山（HC）和模拟退火（SA）操作来改进遗传算法，以获得更好的性能。通过实验，揭示了精确求解方法的局限性，并对所提出的遗传算法的性能进行了比较。结果表明，SAGA可以获得最佳的解决方案质量，而HCGA应该是在解决方案质量和计算时间之间做出良好权衡的选择
引言
多重TSP问题是由旅行商问题（TSP）推广而来的，是一个众所周知的组合优化问题[1]。它旨在确定一个总成本最低的序列，让多个销售人员在给定的一组内访问每个城市一次，并最终返回他们的家乡。MTSP和TSP出现在各种需要解决调度、规划、路线和/或排序问题的应用程序中。在[15]中报告了TSP在机器调度和排序以及车辆路线方面的应用。它们也出现在电路布线[17]和统计数据分析领域，包括排序和聚类对象，例如[32]中的基因排序和[19]中的蛋白质聚类。由于多目标优化算法的最新进展，例如，使用分解和蚁群的多目标进化算法[20]、基于分解的模因算法[21]、雪堆游戏优化[46]、physarum优化[26]，可以显著促进多目标TSP的应用，一种称为多目标多种群的共同进化技术[48]、基于高斯分类器的进化策略[50]、粒子群优化[51]-[56]和基于片段的搜索来改进进化算法[25]。论文[4]对MTSP的应用进行了很好的总结。例如，Gorenstein[14]报道了一本多版本期刊的印刷进度安排。Carter和Ragsdale[5]强调了它在预印本插页广告调度中的应用。报道了在机组人员调度[22]、[40]、[49]、面试调度[13]、劳动力平衡[28]和热轧调度[41]中的应用。自主机器人或车辆运动规划[3]，[33]，[47]代表了MTSP的一个重要应用领域。SarielTa l a y等人[35]以及Toth和Vigo[42]研究了一个车辆路线问题。Cheong和White[7]研究了如何根据实时交通拥堵数据动态确定TSP的行程。最近利用MTSP来规划[9]中无人飞行器所需区域的访问顺序。结果表明，它显著降低了在拥堵的城市环境中实际大小的接送的预期总旅行成本。
从本质上讲，MTSP是对实际问题的抽象，其中涉及多个执行人员（旅行推销员）并共享一个共同的工作空间（城市集）。换句话说，每个销售人员都可以访问MTSP的每个城市。然而，在某些应用程序问题中，并非所有执行个体都具有相同的工作空间。以图1所示的典型多机工程系统multimachine engineering system（MES）的调度为例。单个机器的工作空间不相同，但彼此部分重叠。因此，每台机器不仅要在其专属工作空间中独立执行操作，还要在重叠的工作空间中与其他机器一起完成所有任务。
由于工作空间部分重叠，MTSP无法用于制造执行系统的调度问题建模。然而，这样一个问题的基本要素，即目标、机器个体和任务，仍然可以分别与MTSP的目标、销售人员和城市相匹配。不幸的是，在MTSP中找不到不同任务组在MES中专属和共享工作空间的对应方。通过抽象这些调度问题，我们提出了一种新的具有不同颜色城市集的MTSP，称为有色TSP（CTSP）。这是一个普遍的问题，源于但不限于多机系统的调度问题。因此，它值得在理论和实践上进行大量的研究。
和TSP和MTSP一样，CTSP是NP难的。此外，与MTSP相比，限制性访问使其解决方案更加困难和耗时。许多适当规模的MTSP实例可以通过使用一些精确的方法来解决，例如切割平面法、分支和切割法以及众所周知的分支和定界程序。Gavish和Srikanth[11]提出了一种求解大规模对称MTSP实例的分枝定界算法。结果表明，非欧几里得问题和欧几里得问题的大小分别可达500个城市和10个推销员，以及100个城市和十个推销员。
事实证明，启发式方法比精确方法更快、更有效地求解大型MTSP，可能是以牺牲解的最优性为代价的。因此，它们适用于解决那些令人满意的解决方案就足够了的情况。[18]、[31]、[38]和[43]中也提出了几种从TSP方法扩展而来的人工神经网络方法来求解MTSP.
遗传算法（GA）[45]代表了另一个方向。Zhang等人[49]和Tang等人[41]使用遗传算法来解决热轧调度引起的MTSP。它被转换为单个TSP，并用修改的遗传算法求解。Carter和Ragsdale[6]为MTSP提出了一种新的两部分染色体和相关算子。计算测试表明，他们的方法产生的搜索空间较小，在许多情况下，比那些只有一两条染色体的方法产生更好的解决方案。
Ghafurian和Javadian[12]、Ryan等人[33]和Song等人[39]开发了蚁群、禁忌搜索和模拟退火（SA）算法来求解MTSP。Shim等人[36]提出了一种具有分解的分布混合估计算法来解决多目标MSTP。Sodge等人[37]比较了用于求解MTSP的各种进化计算算法，包括邻域吸引子方案、“收缩包裹”算法、粒子群算法、蒙特卡罗算法、遗传算法和进化策略。
Li等人[23]将CTSP称为MTSP*，并提出了GA解决方案。然而，CTSP并不是以数学上严格的方式制定的。本文的主要贡献是：1）给出了CTSP的正式定义，并通过比较它们的解决方案空间大小，揭示了CTSP、MTSP以及MTSP和TSP组合之间的差异；2） 开发三个GA以有效解决CTSP；以及3）通过实验比较了三种GA的性能和通过LINGO的精确解。比较结果是广泛的，可以用来帮助工程师为特定的CTSP应用选择合适的算法。
接下来，第二节定义并制定CTSP。第三节回顾了GA，并提出了三个改进的GA。第四节对所提出的算法进行了实验和性能比较。本文在第五节中总结。
二、CTSP的定义
A.CTSP定义
假设一个CTSP有m个推销员和n个城市，其中m
V i代表销售人员划分并返回的仓库。我们给销售员i分配颜色i。∀a∈Vi，它的颜色是i，只有销售员i才能访问它。∀a∈U，它的色集是（a）⊆Z m，其中|（a）|>1，如果i∈（a），销售员i可以访问a。CTSP的目标是以最小的总旅行成本确定G上的m个哈密顿循环。这里，每个互斥集的所有顶点都必须由指定的销售人员访问一次，共享集的任何节点都必须由销售人员访问一遍。
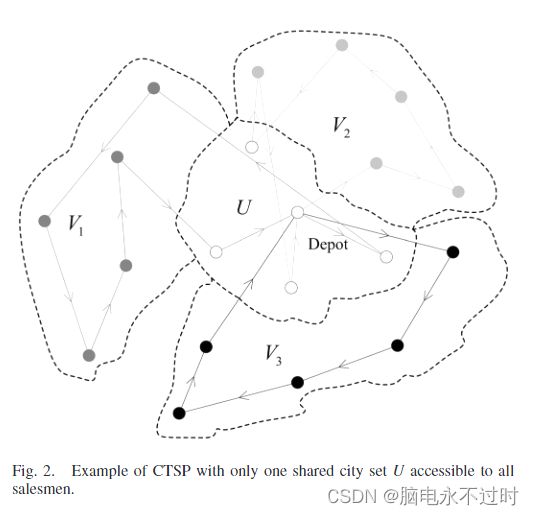
在CTSP中，共享城市集U的组成可以是各种各样的。最常见的一种是U由所有m个销售人员共享，即∀a∈U，color（a）=Zm。一个例子如图2所示。V1−V3区域中的顶点分别代表销售人员1–3的专属城市。U是所有销售人员中唯一的共享城市。销售人员i可以访问Vi U。
当di=0∈U，∀i∈Zm和∀a∈U，c（a）=Zm时，CTSP的整数规划模型如下所示。如果第k个推销员通过边（i，j）, 二元变量
=1，i
j，i，j∈Ş，并且k∈Zm，；否则＝0。
是在第k个销售人员从仓库到节点i的旅程中访问的节点数。问题的目标函数是：
受以下限制：首先，每个销售人员从城市0（仓库）出发并返回，即：
以及：
销售人员k不能从他自己的专属城市开始访问其他销售人员的专属城市，而销售人员k以外的销售人员也被禁止访问后者的专属城市。
销售员l ( l k ) 既不能从销售员k的专属城市开始，也不能返回到k的专属城市。
除城市0外，每个城市都必须由一个销售员精确访问一次：
一个销售员可能会访问一个共享的城市，如果是这样的话，就需要一对进入和离开
Ş\{0}中的节点之间任何不相连的子路线的形成都被以下与（10）相结合的方程所禁止
定理1:CTSP是NP难的。
证据：根据其定义，CTSP是从MTSP中修改而来的，将其城市划分为多个专属城市集和一个共享城市集，并由（4）-（7）制定了额外的可达到的限制。设每个V i，i∈Z m只包含一个城市，并从U中移除城市0。该模型成为多阶段MTSP的一个模型。另一方面，当U＝｛0｝时，对于具有相同仓库0的多个单个TSP，该模型变为一个模型。TSP和MTSP已被证明是NP难[5]，[6]。随着U或V i的恢复，模型的时间复杂性不会因其操作而改变。因此，CTSP是NP难的。
从证据来看，我们得到了以下结果。
推论1：多点MTSP和多个单一TSP是CTSP的特殊情况。
考虑TSP和（由几个单独的TSP组成的）MTSP的组合，每个TSP在一个专属城市集上，而一个MTSP在一个共同城市集上（给定相同的多个销售人员）。CTSP是否可以转换为这样的组合进行解决？答案不是。前者要求多个销售人员在访问所有独家城市或相反的城市后，访问所有共享城市。在CTSP中，销售人员以任意顺序访问不同的城市，包括专属城市和共享城市。因此，由于额外的城市访问限制（可达性），对于相同的问题大小，CTSP的解决方案空间大小不同于这种组合和MSTP。
聚类TSP[8]、[10]、[27]和广义TSP[16]是TSP的两种变体。二者都定义在与TSP相同的图G上。前者旨在确定G上的最小代价哈密顿循环，其中任何簇的顶点都是连续的，而后者旨在找到最小代价回路，其中每个簇恰好出现一个顶点。据作者所知，没有任何工作能将他们与多个销售人员进行概括。CTSP与他们不同，因为它有多个销售人员和不同的共享和专属城市集群。
三、 用于CTSP的GA
A.双染色体表示和解空间分析
由于CTSP的组合复杂性，有必要使用启发式方法来解决相当大的问题。GA代表了一种启发式方法，许多研究人员已经将其应用于TSP和MTSP[5]，[6]，[30]。Li等人[23]开发了一种基本的遗传算法来解决CTSP。[6]中使用的现有单染色体和两部分染色体编码方案由于其城市访问要求而不适用于CTSP。我们将第二节中建模的CTSP的解决方案表示为十进制编码的双染色体，即城市和推销员染色体，个体长度为n−1。所有销售人员的仓库0没有在染色体中编码，而是被添加到最终解决方案中以满足（2）和（3）。第一条染色体具有n−1个城市的排列，而第二条染色体在第一条染色体的相应位置为每个共享和排他性城市分配一个销售员，遵循由（4）–（7）和（10）表示的城市销售员匹配关系。根据（8）和（9），给定任何一代人，一个城市在一个人身上只能出现一次。解决方案编码防止了子巡回的形成，正如（10）和（11）所做的那样
图3显示了n=10和m=3的CTSP编码示例。城市染色体中的基因1和2分别是销售员1的专属城市，销售员2的基因3和4，以及销售员3的基因5和6。它代表了必须满足的城市销售人员匹配关系。共享城市是基因7-10，可以分配给任何销售人员。城市2、8、7和1（按顺序）由销售人员1访问。类似地，销售人员2访问城市10、4和3（按该顺序），销售人员3访问城市9、5和6（按该次序）。
给定一个有m个推销员和n个城市的CTSP，推销员i的独占城市数为ni，共享城市数为n0，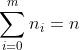
。
定理2：具有双色体编码的CTSP的解空间大小是
。
证明：对于一个拥有n个城市的城市染色体，无论是专属城市还是共享城市，都有n！排列。给定城市的排列，由于城市-销售人员匹配关系（4）-（9）:一，对于任何专属城市，只有一个分配给指定的销售人员；二，对于n0个共享城市中的每一个，都有m个分配给所有销售人员。因此，对于任何城市的排列，销售人员都有
的排列。CTSP的一种解决方案是城市染色体和推销员染色体的组合。因此，CTSP的解空间大小，即双染色体的排列和组合，必须是。
定理3：具有相同大小和双染色体编码的CTSP的解空间大小小于MTSP的解空间，但大于MTSP和TSP的组合的解空间。
证明：如[6]所示，具有双染色体编码的MTSP的解决方案大小为n！米。CTSP n！的解决方案空间大小！m n 0小于n！米。TSP和MTSP的结合意味着每个销售人员对一个专属城市集的访问被视为几个独立的TSP，所有销售人员对共享城市集的参观被视为一个MTSP。解决方案是将两个部分的结果结合起来。对于TSP i，它的城市排列是n i！。将m个TSP视为一个总数，其排列是m！对于具有n0个共享城市的MTSP部分，其排列为n0！m n 0。因此，TSP和MTSP组合的解空间大小是置换（πm1（n i！）×m！）×（n0！mn0）。它比n小！m n 0。因此，结论成立。
这使得CTSP在本质上不同于MSTP以及TSP和MTSP的组合，因为它们在相同问题规模和城市访问限制方面的解决方案空间大小。任何销售人员都可以访问MSTP城市集中的任何城市，而任何销售人员可以访问自己的专属城市和CTSP中任何订单的共享城市。与TSP和MTSP的结合不同，CTSP并非没有要求所有共享城市都必须在他所有的专属城市或相反的城市之后访问。
B.基本GA
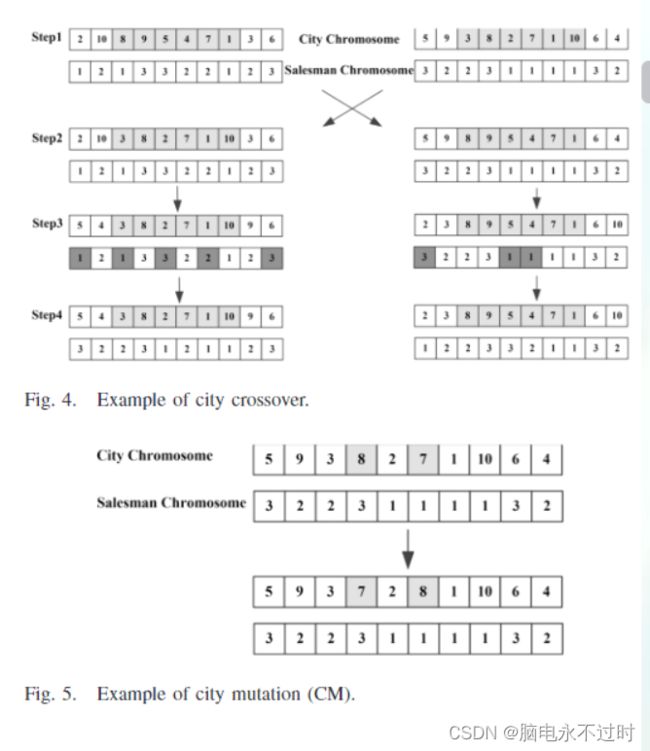
Li等人[23]采用轮盘赌方法和精英策略相结合的方式作为选择操作。他们比较了三对交叉和突变算子的组成，结果表明城市交叉和突变（CCM）的组合具有最好的性能。城市交叉操作是一种改进的部分匹配交叉操作。图4,5显示了双染色体与城市染色体的单次交叉的交叉过程。
首先，从给定父母的两个城市个体中随机选择两个具有相同范围的片段，然后交换这两个片段，从而产生两个新的个体。第二，用符合上述两个片段之间基因交换关系的基因替换两条城市染色体片段外的冗余基因，直到没有多余基因残留。最后，检查每个专属城市是否分配给了正确的销售人员，并纠正错误的分配（如果有的话）。城市交叉的一个例子如图4所示。在步骤1中，灰色的交叉片段被选择到两条城市染色体中，然后它们在相同位置的基因被逐一交换。交换关系为8-3、9-8、5-2、4-7、7-1和1-10。交换会产生两个新的个体，如步骤2所示。在这种交换关系之后，两个片段之外的冗余基因被逐步替换，直到没有发现冗余基因。例如，根据交换关系8-3，位于左城市染色体最后一秒位置的重复基因3应该被8取代。然而，在替换之后，新的基因8仍然是重复的，并且必须根据交换关系9-8再次被基因9替换。由此产生的左侧染色体中的独占城市5、3、7、1和6以及右侧染色体中的城市2、5和4被分配给了错误的销售人员。第4步将他们重新分配给正确的销售人员，并产生两个可行的人选。
双染色体的城市突变过程包括两个步骤，即首先选择城市染色体中的一对基因进行交换；第二，如果需要的话，按照城市推销员匹配关系校正推销员染色体中的两个对应基因。在图5中，选择并交换了基因8和7。它们是共享的城市，可以分配给任何销售人员。因此，城市销售人员匹配关系得到满足，从而突变结束。
适应度函数用于反映如何实现CTSP目标。适应度值越大越好，但总成本越低越好。因此，我们将解x的总成本f的倒数作为适应度函数。
基本遗传算法的过程包括选择、CCM和适应度计算。Li等人[23]指出遗传算法的进化缓慢，很容易陷入局部最优。
C.贪婪初始化的GA(GAG)
贪婪算法在每一步做出的决策可能不会达到全局最优，而是达到局部最优。然而，它可以迅速获得令人满意的解决方案，因为它避免了花费巨大的精力来用尽所有可能性来找到最佳解决方案。我们使用它来优化遗传算法第一步随机生成的初始种群中的个体。高质量的初始种群可以加速遗传算法的种群进化，以快速达到令人满意的解。我们将这种改进的算法命名为具有贪婪初始化的遗传算法，简而言之，就是遗传算法(GAG。
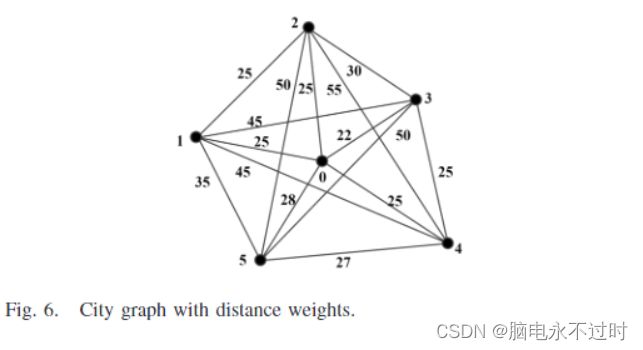
关于CTSP，城市访问需要满足附近的要求。也就是说，当前城市的销售人员选择下一个离它最近的城市。它可以通过重新排序来优化解决方案。例如，如图6所示，随机生成的就诊序列为0→ 2.→ 5.→ 3.→ 1.→ 4.→ 距离之和为25+50+50+45+45+25=240。可以优化为0→ 3.→ 4.→ 5.→ 1.→ 2.→ 0通过使用贪婪算法。新的距离太阳是22+25+27+35+25+25=159，比原来的要小得多。请注意，在某些情况下，边缘权重可能不是距离，例如交通流[44]，然后应将其转换为适当的距离值。
GAG中初始种群的生成过程如下。
步骤1：确定当前初始种群中的个体数量是否等于设定数量N。如果是，请退出。
第二步：随机生成一个城市序列，将独占城市分配给指定的销售人员，将共享城市随机分配给所有销售人员。由此产生的序列被命名为个体a。
第三步：通过最短距离标准对a的城市序列进行重新排序，以最小化访问成本，并获得个人a′。
步骤4：检测群体中是否已经存在a’。如果是，请返回步骤2；否则，将其插入到总体中，然后返回到步骤1。
D.登山GA（HCGA） Hill-Climbing GA
爬山算法利用邻域搜索技术，像爬山一样，在单个方向上进行搜索，以提高解决方案的质量[24]。从现有节点开始，它使用邻域点选择方法生成新的解决方案，并将其与现有节点的值进行比较。如果前者较大，则用前者替换后者；否则，返回后者并将其设置为最大值。重复向上攀爬的过程，直到达到最高点。该算法的局部搜索能力很强，是用于局部最优搜索的常用方法。
所提到的GAG作为一种全局搜索算法，除了个人适合度之外，不利用个人的信息来指导搜索。它的收敛性能是有限的。爬山算法具有很强的局部搜索能力，并且它的搜索是根据个体的质量来引导的。为了提高遗传算法的局部搜索能力，可以通过爬山操作来选择每一代的最佳个体。具体来说，如果通过爬山获得了一个更好的个体，它会取代原来的个体；注意，HCGA也采用了贪婪算法来优化初始种群。
邻域点的选择极大地影响了爬山算法，本工作采用了两点交换。给定有m（≥2）个推销员的CTSP，应该通过这种选择策略选择2M个基因。每次基因交换后，必须重新计算适应度。爬坡操作包括以下步骤。
步骤1：确定执行当前交换的第i个销售员是否是第m个销售员，即i=m。如果是，请退出。
第2步：从a的城市染色体中选择分配给第i个销售员的两个城市基因。交换它们，获得个体a′。
步骤3：确定a′的适应度值是否大于a′的适合度值。如果是，则让a=a′；否则，保留a。
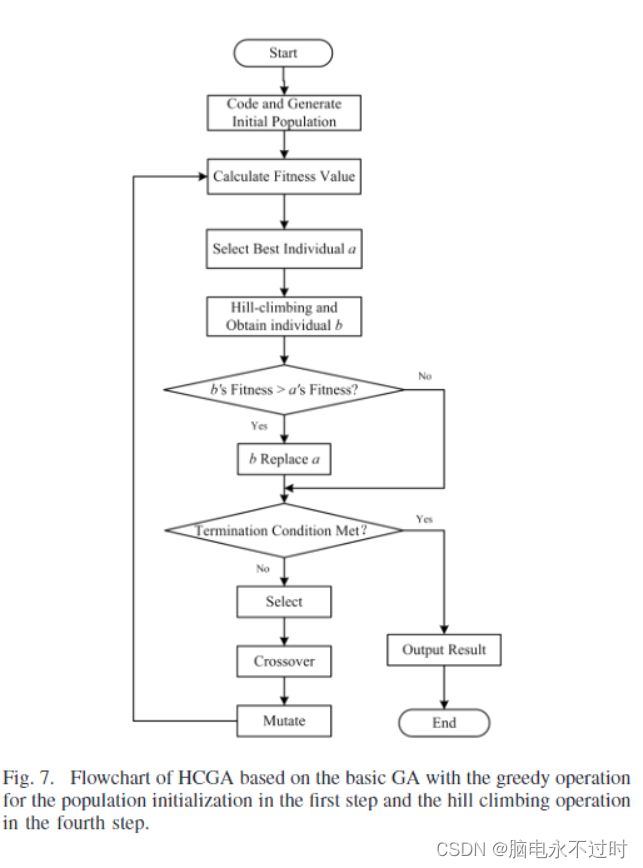
步骤4：设i＝i+1，然后返回步骤1。HCGA的主要程序如图7所示。
图7：基于基本GA的HCGA流程图，第一步是群体初始化的贪心操作，第四步是爬坡操作。
E.SAGA
SA（模拟退火）是一种通用的概率元启发式算法，用于在大搜索空间中定位给定函数的全局最优的良好近似值的全局优化问题[2]。特别是，在搜索过程中，它不仅接受了一个更好的解决方案，而且通过遵循Metropolis准则，以缓慢接近零的概率接受了一个更差的解决方案。它可以跳出局部最优区域，并保证其收敛性能。SA可以用于提高上述GAG的收敛性。
CTSP的解和最优解依次与SA中每个粒子的状态和粒子的最低能量状态相似。CTSP达到最短路径的目标函数对应于SA能量函数。通过设置适当的初始温度并遵循设计的一些冷却计划，SA可以解决CTSP。
SA和GA可以以两种常见的方式组合，即分别在选择、交叉和突变之前和之后对：1）每个个体和2）GA群体中最好的个体进行SA。由于种群数量大，染色体长，前者需要太多时间。相反，这项工作采用了后者。
SAGA程序如下所示。
步骤1：设置初始温度t0，并生成初始历元l=0的GA，P（0）的初始种群。
步骤2：如果满足GA的终止条件，则进入步骤7；否则，计算种群P（l）中每个个体的适应度，并根据获得的适应度值对个体进行选择、交叉和突变，以获得新的种群P1。
步骤3：选择P1中最好的个体作为SA的初始解x 0。让当前温度t 0，当前冷却次数k=0。
步骤4：如果在每个温度下都达到迭代步长，则转到步骤5。否则，从当前解x的邻域中随机选择一个可行的邻域x′，并用Metropolis准则确定是否接受它。即，计算f=f（x′）−f（x），如果f≤0，则x=x′；否则，如果exp（−f/t k）>r，其中r是通过对（0，1）上的均匀分布进行采样而获得的随机数，则重复步骤4。
步骤5：设k=k+1，t k=α•t k，其中α是冷却系数。证明SA的终止条件是否满足。如果没有，请转到步骤4。
步骤6：将P1中的原始个体替换为SA获得的个体，以获得新的群体P2。Letl=l+1，P（l）=P2。转到步骤2
步骤7：输出结果。
SAGA的流程图类似于图7所示，其中需要用SA代替爬山操作。
四、 实验和结果
进行了实验，比较了所提出的算法在求解CTSP方面的性能。首先，LINGO软件作为整数规划的综合工具，用于精确求解给定的整数规划模型。通过一组实验说明了LINGO精确解的不足。然后，通过案例研究，可以观察测试算法的具体演变和求解过程，并随后分析它们的收敛速度和求解质量。最后，使用几个不同大小的CTSP案例，对它们的求解质量和计算时间进行了全面的统计分析和比较。
A.LINGO与GA之比较
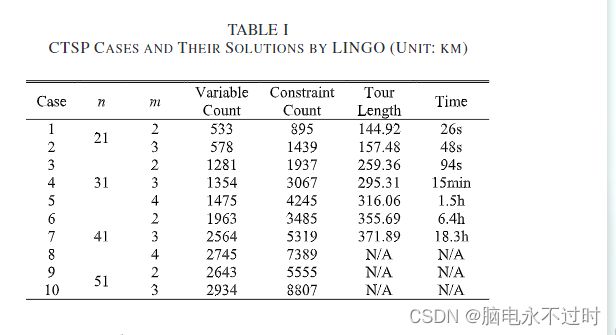
在表I中，设计了十个CTSP案例，其中所有城市数据都来自TSP集合TSPLIB中的数据集eil51，引用于http://people.sc.fsu.edu/~jburkardt/datasets/tsp/tsp.html。共享和独占城市集的具体划分包含在在线补充文件中。使用的计算机是运行Windows 7（32位）的Dell Inspiron 620s，CPU为Intel Corei3，RAM为2 GB，频率为3.30 GHz。结果如表I所示。
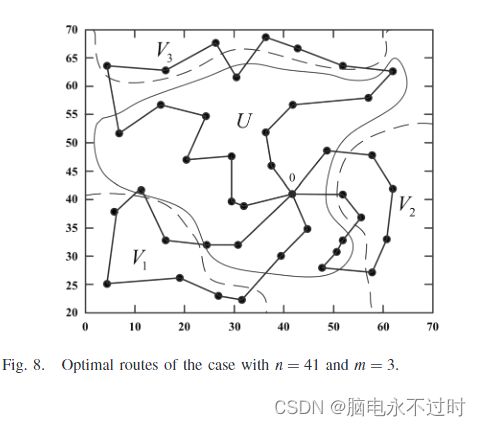
对应于第七种解决方案的最佳路线如图8所示。但后三种情况无法在两天内解决。销售人员在其专属城市和共享城市之间穿梭的设置如图8所示。请注意，将TSP和MTSP结合起来是不可能获得这样的解决方案的。
与MTSP相比，销售人员对专属城市访问的限制使其解决方案更加困难和耗时。当CTSP的大小很小时，例如，n＜41时，LINGO可以快速解决问题。然而，随着n和m的增加，时间消耗急剧增加。例如，给定n=31的两种情况，当m=2时，所消耗的时间仅为94秒，而当m=3时，则增加到15分钟。这主要是由于约束数量的急剧增加，即如表I的第四列所示，m=2有1937个约束，而m=3有3067个约束。这导致计算时间的大幅增加。对于m=3的两种情况，对于n=21、31和41，消耗的时间分别为26s、94s和6.4h。变量和约束的数量呈指数级增长。随着CTSP规模的进一步增加，其精确求解变得越来越困难。例如，从n=41和m=4开始，其解决方案不能在两天内通过LINGO获得。
接下来，我们确认在CTSP的求解中，GA是否比精确方法更快、更有效。我们将参数，即群体的大小设置为30，交叉概率设置为0.7，突变概率设置为0.1。每个算法运行十次，最大epoch为2000。设定与SA操作相关的参数，即初始温度为100，冷却总时间60，每个温度下的步长30，以及退火系数0.9。
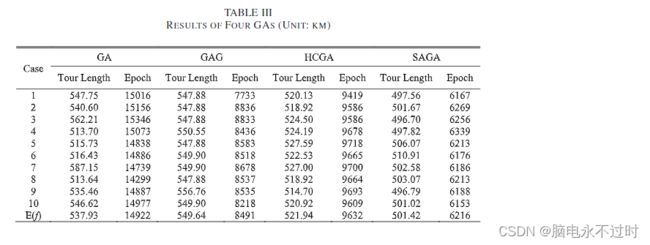
表II列出了表I中的10个案例和4个GA的结果。随着案例大小的增加，GA所花费的时间的增加要比LINGO慢得多。例如，对于三个销售人员和不断增加的城市的情况，GA的时间消耗的增加不超过40秒，而LINGO的时间消耗增加了十倍或更多。对于31个城市的案例，随着销售人员的增加，他们在LINGO上花费的时间增加了约10倍和6倍，但在GA上的时间波动很小，不到8秒。
遗传算法总是可以获得一个解，但不一定是最优解。根据表II，在2000个epoch的终止条件下，使用HCGA和SAGA的解决方案接近使用LINGO的可用精确解决方案。SAGA实现了最佳的解决方案质量，平均、最大和最小误差分别为3.54、9.8和0.56km。GA适用于解决（由于最优解决方案成本过高）但（高质量解决方案就足够）的情况。
B.GA情况研究
n=51和m=4的CTSP如图10所示，其中U是共享城市集，V 1−V 4分别是销售人员1−4的专属城市集（访问区域）。使用了前面提到的同一台计算机。接下来，将GA、GAG、HCGA和SAGA四种算法应用于解决该问题，并对它们的性能进行了比较。根据我们的经验，算法的终止条件变为10分钟，以确保它们之间的公平性，而它们的其他参数保持不变。结果如表III所示。
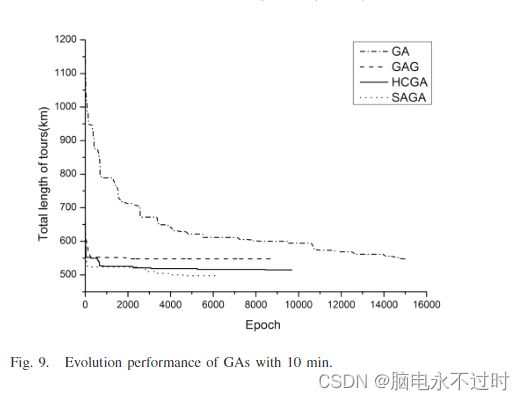
1） 收敛速度：为了比较它们的收敛速度，我们绘制了它们获得的个体的最佳收敛过程，如图9所示。GA中最佳初始个体的总行程约为1200公里。通过贪婪操作，GAG、HCGA和SAGA中初始种群的质量大大提高。对于相同的时间终止条件，它们比基本GA收敛得更快。四个GA分别在第15000个、第8500个、第9600个和第6200个epoch终止。然而，后三个GA的实际进化分别在第8000、850和5000个时期更早完成。基本GA的收敛非常缓慢，并且进化似乎不会在大约15000世结束。这显然比其他的要耗时得多。
此外，SAGA是其中最好的，而HCGA在收敛速度上优于GAG。在没有爬山操作的情况下，由于其在本地搜索方面的弱点，GAG需要大约2000个历元才能进化到总行程为550公里的结果；而SAGA和HCGA仅花费约150和300个时期来实现相同或更好的结果。在HCGA的演化结束于第8500个历元，总行程约为520km后，SAGA可以继续演化，直到第5000个历元左右，总行程长度约为500km。
2） 解决方案质量：从图9中，我们发现GA和GAG都很难在第15000个和第8500个时期达到最佳结果，总行程长度分别约为540和550。很明显，在达到GAG的相同结果后，HCGA可以继续收敛到更好的解，如图9所示，由于爬山操作的强大局部搜索能力。但在9500个epoch左右，它停止了。它可能会陷入局部最优。
SAGA十次实验的平均行程长度为501.42。与GA、GAG和HCGA相比，它分别实现了37个、49个和21个单位的行程缩短。这表明SA运算可以提高遗传算法的收敛性能和逃离局部最优的可能性。使用SAGA的最佳解决方案的总行程长度为496.70，如图10所示。
总之：1）由于在遗传算法中引入了SA运算，SAGA的收敛速度在三种考虑的遗传算法中是最高的；2）SAGA可以更容易地摆脱局部最优，并在四种算法中产生更好的解。
C、 遗传算法的分组实验
1） 实验设置：我们设计了三组，11个实验案例，对算法的性能进行综合分析。CTSP的三组依次分配的城市规模，分别为51、76和101。所有城市数据均来自TSPLIB中的数据集eil51、eil76和eil101，共享城市集和各种独占城市集根据表IV进行分组。城市分布如在线补充文件所示。表IV是参考Taguchi方法进行设计和优化的。其中，尽可能平均地划分每种情况下的不同专属城市集，共享城市在所有城市中的比例在0.2到0.5之间波动。这可以防止CTSP成为MTSP或多个单独的TSP。这三组包括各种典型案例。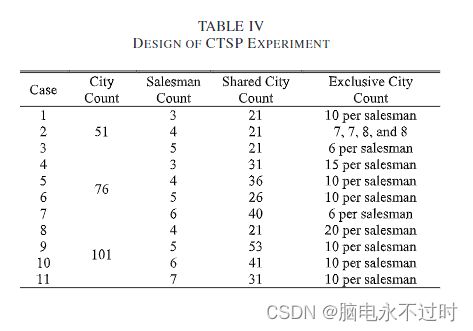
将所提出的四种算法应用于解决这些情况。为了解决方案质量比较的公平性，允许每个算法的解决方案充分发展。因此，所有GA的最大epoch被设置为10000。随着城市数量的增加，GA的初始种群规模应该相应增加。每个病例的初始人群规模设置为40人。四种算法的交叉率和突变率分别设置为相同的0.9和0.1。对于HCGA，爬山次数被设置为50，而对于SAGA，初始温度被设置为100，退火次数为50，每个温度下的迭代次数为30，冷却系数为0.9。
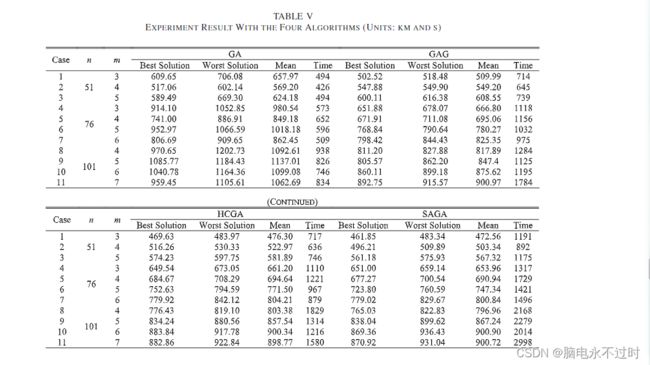
2） 解决方案质量：表五给出了表四中设计的分组实验的结果。每个案例通过使用每种算法运行十次。表五记录了每种情况下十个样本的最佳、最差和平均解的统计数据以及相应的时间消耗。通过观察表V，我们发现无论最佳、最差和平均解如何，GA获得的解的质量在所有情况下都是最差的。其背后的原因是其收敛速度慢，容易陷入局部最优，如图所示。其余算法、GAG、HCGA和SAGA实现了更好的解质量。
通过使用贪婪操作，GA的初始种群变得更好。然而，遗传算法最大的缺陷仍然存在于遗传算法中，即容易陷入局部最优。由于HCGA引入了爬山操作来增强GAG的局部搜索能力，因此它在每个最佳和平均结果上几乎都优于GAG。然而，对于101个城市的案例，前者的解决方案质量比后者差。原因是病例数量的增加更有可能导致爬山的挑战性问题，例如收敛到局部最大值、山脊和小巷。SAGA几乎取得了其中最好的结果。其原因是SA本身是一种全局算法，能够摆脱局部最优，而爬山算法只是一种局部算法。此外，SAGA最佳解决方案的增长随着案例规模的增加而最为稳定。
3） 时间消耗：
我们试图根据表V中给出的实验结果来分析GA的时间消耗。所有算法的时间消耗都随着城市规模的增长而增加。例如，随着城市数量从51增加到101，基本GA和SAGA分别消耗471到836秒和1086到2365秒的平均时间。同时，从结果中可以观察到算法的时间消耗的不同增长率。SAGA的增长最大，其次是HCGA、GAG和基本GA。这表明贪婪、爬山和SA操作的引入会导致更多的计算时间，并且案例的大小越大，计算时间就越长。
对于相同大小的情况，从最小到最大的时间消耗顺序为GA、GAG和HCGA，以及SAGA。例如，为了解决101个城市和4个销售人员的情况，GA消耗938 s，GAG 1284 s，爬山1829 s，SAGA 2168 s。这表明贪婪初始化或爬山的引入消耗了额外的时间。因此，对于相同的案例大小，GAG需要比GA更多的计算时间。HCGA比GAG更耗费时间来达到相同的终止时期。SAGA同时利用贪婪初始化策略和SA，后者比爬山更复杂。因此，它比HCGA更耗时。
在相同城市数的情况下，算法的时间消耗与销售人员的增长没有一致性。例如，在101个城市的案例中，所有GA消耗的时间并不仅仅是增加或减少。这表明，对于一个算法来说，其解决CTSP的时间消耗可能受到许多因素的影响，包括销售人员数量、共享城市集和独占城市集的划分。计算时间和这些因素之间的关系非常复杂。目前的实验很难分析，我们打算在未来考虑。
D.总结和讨论
CTSP适用于一些应用程序问题，在这些问题中，多个旅行的个人不仅要处理他们自己的专属任务，还要处理允许其中一个执行的共享任务组。例如，包含径向排列的单个机器的多个机器系统的调度，这些机器的工作空间共享一个公共部分，可以公式化为CTSP来解决。如图1所示的MES的调度可以转换为具有两个销售人员的CTSP的典型情况。
在制定问题之前，应按照一些过程要求对要由多台机器执行的任务（如平面或空间的点、线和曲线）进行划分和分配。然后，应该将分配的任务抽象为图的顶点。顶点和单个机器最终分别被建模为CTSP中的城市和销售人员。具体地说，每组专属（共享）工作被表示为一组专属（共享的）城市。调度目标是为每台机器搜索作业序列，使得所有机器的总作业执行成本最小。它可以通过相应的CTSP的目标函数来制定，并对访问成本进行适当的定义。
根据上述实验结果，如果只考虑解决方案质量，SAGA是解决实际尺寸的CTSP的最佳选择；而如果需要在相对较短的时间内获得良好的解决方案，则建议使用HCGA。据作者所知，Gavish和Srikanth[11]解决的最大规模MTSP有500个城市。由于CTSP对城市可达性和城市分区对销售人员的限制，对于相同的问题规模，它需要比MTSP更多的时间和内存，因此我们将这些大规模案例推迟到未来的研究中。
V.结论
在本文中，我们提出了一种新的MTSP，称为CTSP，不同的销售人员拥有专属的城市集，并共享一组共同的城市。它源于多个个人在不同但部分重叠的工作空间中协同工作的应用程序。本文以数学上严谨的方式阐述了这个新问题。我们提出了三种遗传算法，即贪婪初始化遗传算法、爬坡遗传算法和模拟退火遗传算法，它们是在基本遗传算法的基础上改进而来的。利用其中的双染色体编码推导了解的空间大小。分析了CTSP、MTSP以及MTSP和TSPs的组合之间的差异。通过与四种遗传算法的比较，揭示了LINGO软件精确求解CTSP方法的能力和局限性。通过实验，全面比较了遗传算法在进化率、求解质量和时间消耗方面的性能。结果表明，SAGA可以获得最佳解决方案，而HCGA可以在相对较短的时间内获得高质量的解决方案。未来的工作旨在处理现有方法无法处理的大型CTSP及其在MES优化操作中的应用。人们非常希望快速评估CTSP最优解的下界，它可以作为一个指标来评估和比较不同的智能优化方法[20]、[21]、[25]、[26]、[46]、[48]、[50]-[62]的解质量。快速方法[64]-[72]可以用于这种目的。