蓝桥杯·3月份刷题集训Day03
本篇博客旨在记录自已打卡蓝桥杯3月份刷题集训,同时会有自己的思路及代码解答希望可以给小伙伴一些帮助。本人也是算法小白,水平有限,如果文章中有什么错误之处,希望小伙伴们可以在评论区指出来,共勉。
文章目录
-
- 集训A
-
- A1、扫雷
- A2、含2天数
- 集训B
-
- B1、杨辉三角形
- B2、谈判
- 集训C
-
- C1、买不到的数目
- C2、画廊
- 最后
集训A
A1、扫雷
题目:在一个 n 行 m 列的方格图上有一些位置有地雷,另外一些位置为空。
请为每个空位置标一个整数,表示周围八个相邻的方格中有多少个地雷。
输入格式:
输入的第一行包含两个整数 n,m。
第 2 行到第 n+1 行每行包含 m 个整数,相邻整数之间用一个空格分隔。如果对应的整数为 0,表示这一格没有地雷。如果对应的整数为 1,表示这一格有地雷。
其中,1≤n,m≤100 分钟后还是在当天。
输出格式:
输出 n 行,每行 m 个整数,相邻整数之间用空格分隔。
对于没有地雷的方格,输出这格周围的地雷数量。对于有地雷的方格,输出 9。
输入输出样例:
输入
3 4
0 1 0 0
1 0 1 0
0 0 1 0
输出
2 9 2 1
9 4 9 2
1 3 9 2
运行限制:
- 最大运行时间:1s
- 最大运行内存: 128M
解题代码:
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
/**
* 2021 模拟赛 模拟 暴力
* 扫雷
* @author QIA
* @create 2023-03-24-9:43
*/
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int map[][] = new int[n+2][m+2];
int result[][] = new int[n+2][m+2];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
map[i][j] = sc.nextInt();
}
}
int sum = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if(map[i][j] == 1) {
result[i][j] = 9; // 存在地雷赋给9
}else {
sum = map[i][j] + map[i-1][j-1] + map[i-1][j] + map[i-1][j+1] +
map[i][j-1] + map[i][j+1] + map[i+1][j-1] + map[i+1][j] + map[i+1][j+1];
result[i][j] = sum;
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
System.out.print(result[i][j] + " ");
}
System.out.println();
}
}
}
A2、含2天数
题目:
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝特别喜欢 22,今年是公元 20202020 年,他特别高兴,因为每天日历上都可以看到 22。
如果日历中只显示年月日,请问从公元 19001900 年 11 月 11 日到公元 99999999 年 1212 月 3131 日,一共有多少天日历上包含 22。即有多少天中年月日的数位中包含数字 22。
运行限制:
- 最大运行时间:1s
- 最大运行内存: 128M
解题代码:
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
//判断输入的数是否含2
static boolean check(int a) {
while (a > 0) {
if (a % 10 == 2)
return true;
a /= 10;
}
return false;
}
public static void main(String[] args) {
int[] day = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int ans = 0;
for (int i = 1900; i <= 9999; i++) {
if ((i % 4 == 0 && i % 100 != 0) || i % 400 == 0) {//闰年
day[1] = 29;
} else {
day[1] = 28;
}
// if(check(i)) //如果在这里判断,每一年只会判断一次,少判断了,要把年月日合起来,有了就算
// ans++;
for (int month = 1; month <= 12; month++) {
// if(check(month))
// ans++;
for (int d = 1; d <= day[month - 1]; d++) {
if (check(d) || check(i) || check(month))
ans++;
}
}
}
System.out.println(ans);
}
}
集训B
B1、杨辉三角形
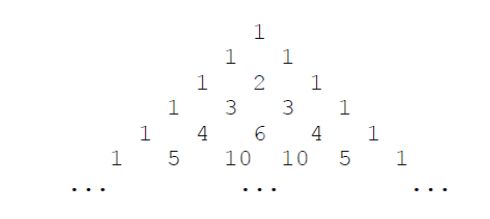
题目:下面的图形是著名的杨辉三角形:
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列: 1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯
给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
输入格式:
输入一个整数 N。
输出格式:
输出一个整数代表答案。
输入输出样例:
输入
6
输出
13
评测用例规模与约定:
对于 20 的评测用例,1≤N≤10; 对于所有评测用例,1≤N≤1000000000。
运行限制:
- 最大运行时间:1s
- 最大运行内存: 256M
解题代码:
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
//在此输入您的代码...
long num = scan.nextLong();
int loc=1;
boolean flag =true;
if(num==1){
System.out.println(1);
flag=false;
}
for(int i=16;i>1;i--){//从内侧第16根开始找,i表示层间索引,j表
if(flag){
int j =2*i;
while(comb(i, j)<=1e9){
if(comb(i, j)==num){
loc = j*(j+1)/2+i+1;
System.out.print(loc);
flag=false;
break;
}
j++;
}
}
}
if(flag){
System.out.print(num*(num+1)/2+2);
}
scan.close();
}
public static long comb(int a,int b){
long res =1;
int c =1;
for(int i=b;i>0&&i>=(b-a+1);i--,c++){
res*=i;
res/=c;
}
return res;
}
}
B2、谈判
题目:在很久很久以前,有 n 个部落居住在平原上,依次编号为 1 到 n。第 i 个部落的人数为 ti。
有一年发生了灾荒。年轻的政治家小蓝想要说服所有部落一同应对灾荒,他能通过谈判来说服部落进行联合。
每次谈判,小蓝只能邀请两个部落参加,花费的金币数量为两个部落的人数之和,谈判的效果是两个部落联合成一个部落(人数为原来两个部落的人数之和)。
输入格式:
输入的第一行包含一个整数 n,表示部落的数量。
第二行包含 n 个正整数,依次表示每个部落的人数。
其中,1≤n≤1000,1≤*ti*≤104。
输出格式:
输出一个整数,表示最小花费。
输入输出样例:
输入
4
9 1 3 5
输出
31
运行限制:
- 最大运行时间:1s
- 最大运行内存: 128M
解题代码:
import java.util.Arrays;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
int len = sc.nextInt();
int[] nums = new int[len];
for(int i=0;i<len;i++) {
nums[i] = sc.nextInt();
}
Arrays.sort(nums);
int sum = 0;
// 找到规律前两个数加(n-1)次,后面的数字加(n-其下标)次
for(int i=1;i<=len;i++) {
sum = sum+i*nums[len-i];
}
// 注意到nums[0]多加了一次
sum = sum-nums[0];
System.out.println(sum);
sc.close();
}
}
集训C
C1、买不到的数目
题目:小明开了一家糖果店。他别出心裁:把水果糖包成 4 颗一包和 7 颗一包的两种。糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是 17。大于 17 的任何数字都可以用 4 和 7 组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入格式:
输入两个正整数,表示每种包装中糖的颗数(都不多于 1000 )。
输出格式:
输出一个正整数,表示最大不能买到的糖数。
不需要考虑无解的情况
输入输出样例:
输入
4 7
输出
17
运行限制:
- 最大运行时间:3s
- 最大运行内存: 64M
解题代码:
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int a=scan.nextInt();
int b=scan.nextInt();
System.out.println(a*b-(a+b));
scan.close();
}
}
C2、画廊
题目:小蓝办了一个画展,在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思,小蓝没有等距陈列自己的作品,而是按照更有艺术感的方式陈列。
在画廊的左边陈列了 L 幅作品,在画廊的右边陈列了 R 幅作品,左边的作品距离画廊的起点依次为 u*1,u2,⋅⋅⋅,uL,右边的作品距离画廊起点依次为 v1,v2, ⋅⋅⋅ , vR。
每周,小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的,但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。
小蓝从画廊的起点的正中央(左右两边的中点)出发,整理好每一幅画,最终到达画廊的终点的正中央。已知画廊的宽为 w。
请问小蓝最少带着工具走多长的距离?
输入格式:
输入的第一行包含四个整数 L,R,d,w,表示画廊左边和右边的作品数量,以及画廊的长度和宽度。
第二行包含 L 个正整数 u*1,*u 2, ⋅⋅⋅ , uL,表示画廊左边的作品的位置。
第三行包含 R 个正整数 v*1,v2 , ⋅⋅⋅ , vR,表示画廊右边的作品的位置。
其中有,1 ≤ L , R ≤ 500 , 1 ≤ d ≤ 105,1 ≤ w ≤ 105, 0 ≤ u 1 < u2 < ⋅⋅⋅ < uL ≤ d , 0 ≤ v1 < v 2 < ⋅⋅⋅ < vR ≤ d 。
输出格式:
输出一个实数,四舍五入保留两位小数,表示小蓝最少带着工具走的距离。
输入输出样例:
输入
3 3 10 2
1 3 8
2 4 6
输出
14.71
运行限制:
- 最大运行时间:1s
- 最大运行内存: 128M
解题代码:
import java.util.Scanner;
public class Main {
static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int l = sc.nextInt();
int r = sc.nextInt();
int d = sc.nextInt();
double w = sc.nextDouble();
double wr = w / 2;
int[] ls = new int[l + 1];
int[] rs = new int[r + 1];
for (int i = 1; i < l + 1; i++) {
ls[i] = sc.nextInt();
}
for (int i = 1; i < r + 1; i++) {
rs[i] = sc.nextInt();
}
double[][][] dp = new double[l + 1][r + 1][2];
for (int i = 0; i < l + 1; i++) {
for (int j = 0; j < r + 1; j++) {
dp[i][j][0] = INF;
dp[i][j][1] = INF;
}
}
double a = f(wr, ls[1]);
double b = f(wr, rs[1]);
dp[1][0][0] = a;
dp[0][1][1] = b;
for (int i = 2; i < l + 1; i++) {
dp[i][0][0] = a + ls[i] - ls[1];
}
for (int i = 2; i < r + 1; i++) {
dp[0][i][1] = b + rs[i] - rs[1];
}
for (int i = 1; i < l + 1; i++) {
for (int j = 1; j < r + 1; j++) {
dp[i][j][0] = Math.min(dp[i - 1][j][0] + ls[i] - ls[i - 1], dp[i - 1][j][1] + f(w,ls[i] - rs[j]));
dp[i][j][1] = Math.min(dp[i][j - 1][1] + rs[j] - rs[j - 1], dp[i][j - 1][0] + f(w,rs[j] - ls[i]));
}
}
double ltop=dp[l][r][0]+f(wr,d-ls[l]);
double rtop=dp[l][r][1]+f(wr,d-rs[r]);
System.out.printf("%.2f",Math.min(ltop, rtop));
}
private static double f(double a, double b) {
return Math.sqrt(a * a + b * b);
}
}
最后
有帮助的话,希望可以点赞❤️+收藏⭐,谢谢各位大佬~~