动态规划——线性dp
基于数字三角形问题扩展
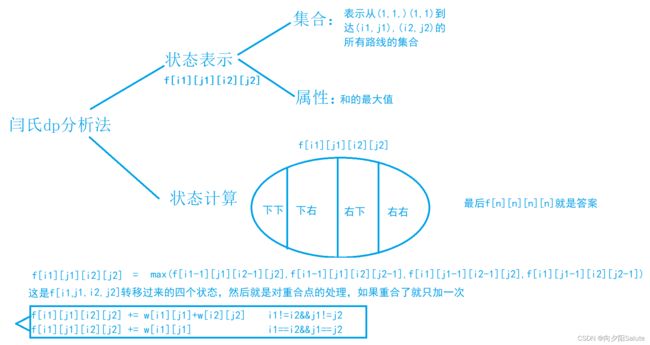
参考闫氏 d p 分析法 参考闫氏dp分析法 参考闫氏dp分析法
方格取数
f [ i 1 ] [ j 1 ] [ i 2 ] [ j 2 ] 表示( 1 , 1 )到( i 1 , j 1 )和( 1 , 1 )到 ( i 2 , j 2 ) 和的最大值 f[i1][j1][i2][j2]表示(1,1)到(i1,j1)和(1,1)到(i2,j2)和的最大值 f[i1][j1][i2][j2]表示(1,1)到(i1,j1)和(1,1)到(i2,j2)和的最大值
利用最后一步不同的思想,找个集合可以由四种状态转移过来 利用最后一步不同的思想,找个集合可以由四种状态转移过来 利用最后一步不同的思想,找个集合可以由四种状态转移过来
分别是 ( i 1 , j 1 ) 由 ( i 1 − 1 , j 1 ) 向下得来或者 ( i 1 , j 1 − 1 ) 向右得来的两种情况和 ( i 2 , j 1 ) 分别由 ( i 2 − 1 , j 2 ) , ( i 2 , j 2 − 1 ) 两种情况组合而成 分别是(i1,j1)由(i1-1,j1)向下得来或者(i1,j1-1)向右得来的两种情况和(i2,j1)分别由(i2-1,j2),(i2,j2-1)两种情况组合而成 分别是(i1,j1)由(i1−1,j1)向下得来或者(i1,j1−1)向右得来的两种情况和(i2,j1)分别由(i2−1,j2),(i2,j2−1)两种情况组合而成
这个题还有个限制就是每个方格只能取一次,所有 ( i 1 , j 1 ) , ( i 2 , j 2 ) 到了相同的点只需要加一次权值 这个题还有个限制就是每个方格只能取一次,所有(i1,j1),(i2,j2)到了相同的点只需要加一次权值 这个题还有个限制就是每个方格只能取一次,所有(i1,j1),(i2,j2)到了相同的点只需要加一次权值
四维代码
#include 四维的 f [ i 1 ] [ j 1 ] [ i 2 ] [ j 2 ] 是 ( 1 , 1 ) ( 1 , 1 ) 到 ( i 1 , j 1 ) ( i 2 , j 2 ) 路线的集合 四维的f[i1][j1][i2][j2]是(1,1)(1,1)到(i1,j1)(i2,j2)路线的集合 四维的f[i1][j1][i2][j2]是(1,1)(1,1)到(i1,j1)(i2,j2)路线的集合
我们发现重合点一定是偏移量相同时 ( i 1 + j 1 = = i 2 + j 2 ) 才可能重合 我们发现重合点一定是偏移量相同时(i1+j1==i2+j2)才可能重合 我们发现重合点一定是偏移量相同时(i1+j1==i2+j2)才可能重合
上面那个思路 i 1 + j 1 和 i 2 + j 2 是没关系的,但我们可以加一个 k 当作偏移量 上面那个思路i1+j1和i2+j2是没关系的,但我们可以加一个k当作偏移量 上面那个思路i1+j1和i2+j2是没关系的,但我们可以加一个k当作偏移量
k = i 1 + j 1 = i 2 + j 2 k=i1+j1=i2+j2 k=i1+j1=i2+j2
这样 f [ k ] [ i 1 ] [ i 2 ] 就相当于偏移量相同的 ( 1 , 1 ) ( 1 , 1 ) 到 ( i 1 , k − i 1 ) ( i 2 , k − i 2 ) 这样f[k][i1][i2]就相当于偏移量相同的(1,1)(1,1)到(i1,k-i1)(i2,k-i2) 这样f[k][i1][i2]就相当于偏移量相同的(1,1)(1,1)到(i1,k−i1)(i2,k−i2)
这样我们就实现了代码的优化 这样我们就实现了代码的优化 这样我们就实现了代码的优化
三维代码
#include 扩展 扩展 扩展
传字条的题目与这个题目的区别就是重复的点不可以过,而这个题是重复的点可以过但取为 0 传字条的题目与这个题目的区别就是重复的点不可以过,而这个题是重复的点可以过但取为0 传字条的题目与这个题目的区别就是重复的点不可以过,而这个题是重复的点可以过但取为0
但是相同的代码可以同样 a c 原因就是在递推的过程中虽然枚举了重复的点,但这个重复的点一定不是最优解,会被最终的最优解覆盖掉,最终答案也一定是不含重复点的两条路线的最大和 但是相同的代码可以同样ac原因就是在递推的过程中虽然枚举了重复的点,但这个重复的点一定不是最优解,会被最终的最优解覆盖掉,最终答案也一定是不含重复点的两条路线的最大和 但是相同的代码可以同样ac原因就是在递推的过程中虽然枚举了重复的点,但这个重复的点一定不是最优解,会被最终的最优解覆盖掉,最终答案也一定是不含重复点的两条路线的最大和