蓝桥杯模板题目
A:::::::::::::::小王子单链表(链表)
题目描述
小王子有一天迷上了排队的游戏,桌子上有标号为 1−10 的 10 个玩具,现在小王子将他们排成一列,可小王子还是太小了,他不确定他到底想把那个玩具摆在哪里,直到最后才能排成一条直线,求玩具的编号。已知他排了 M 次,每次都是选取标号为 X 个放到最前面,求每次排完后玩具的编号序列。
要求一:采用单链表解决
输入描述
第一行是一个整数 M,表示小王子排玩具的次数。
随后 M 行每行包含一个整数 X,表示小王子要把编号为 X 的玩具放在最前面。
输出描述
共 M 行,第 i 行输出小王子第 i 次排完序后玩具的编号序列。
输入输出样例
示例 1
输入
5
3
2
3
4
2
输出
3 1 2 4 5 6 7 8 9 10
2 3 1 4 5 6 7 8 9 10
3 2 1 4 5 6 7 8 9 10
4 3 2 1 5 6 7 8 9 10
2 4 3 1 5 6 7 8 9 10#include
#include
using namespace std;
list a;
int m[15];
int M;
int main(){
cin>>M;
for(int i=1;i<=10;i++){
a.push_back(i);
}
while(M--){
int x;
cin>>x;
a.remove(x);
a.push_front(x);
for(list::iterator it=a.begin();it!=a.end();it++){
cout<<*it<<' ';
}
cout<
B:::::::::::::::蓝桥公园(Floyd)
题目描述
小明喜欢观景,于是今天他来到了蓝桥公园。
已知公园有 N 个景点,景点和景点之间一共有 M 条道路。小明有 Q 个观景计划,每个计划包含一个起点 st 和一个终点 ed,表示他想从 st 去到 ed。但是小明的体力有限,对于每个计划他想走最少的路完成,你可以帮帮他吗?
输入描述
输入第一行包含三个正整数 N,M,QN,M,Q
第 2 到 M+1 行每行包含三个正整数 u,v,w,表示 u↔v 之间存在一条距离为 w 的路。
第 M+2 到 M+Q−1 行每行包含两个正整数 st,ed,其含义如题所述。
1≤N≤400,1≤M≤2N×(N−1),Q≤103,11≤u,v,st,ed≤n,1≤w≤109
输出描述
输出共 QQ 行,对应输入数据中的查询。
若无法从 stst 到达 eded 则输出 -1−1。
输入输出样例
示例 1
输入
3 3 3
1 2 1
1 3 5
2 3 2
1 2
1 3
2 3
输出
1
3
2#include
#include
#include
using namespace std;
long long n,m,q; //n个 景点,m条路,q个计划;
long long lu[1000][1000];
int main(){
memset(lu,0x3f3f3f3f3f3f3f3f,sizeof(lu));
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
lu[i][i]=0;
}
for(int i=1;i<=m;i++){
long long a,b,c;
cin>>a>>b>>c;
lu[a][b]=lu[b][a]=min(lu[a][b],c);
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(lu[i][j]>lu[i][k]+lu[k][j]){
lu[i][j]=lu[i][k]+lu[k][j];
}
}
}
}
for(int i=0;i>a>>b;
if(lu[a][b]==0x3f3f3f3f3f3f3f3f){
cout<<-1< C:::::::::::::::付账问题
题目描述
几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。
现在有 n 个人出去吃饭,他们总共消费了 S 元。其中第 i 个人带了 ai元。幸运的是,所有人带的钱的总数是足够付账的,但现在问题来了:每个人分别要出多少钱呢?
为了公平起见,我们希望在总付钱量恰好为 S 的前提下,最后每个人付的钱的标准差最小。这里我们约定,每个人支付的钱数可以是任意非负实数,即可以不是 1 分钱的整数倍。你需要输出最小的标准差是多少。
标准差的介绍:标准差是多个数与它们平均数差值的平方平均数,一般用于刻画这些数之间的"偏差有多大"。形式化地说,设第 ii个人付的钱为 bi 元,那么标准差为 :
输入描述
第一行包含两个整数 n、Sn、S;
第二行包含 n 个非负整数 1, ⋯, an。
其中,n≤5×105,0≤ai≤109 。
输出描述
输出最小的标准差,四舍五入保留 4 位小数。
保证正确答案在加上或减去 10−9 后不会导致四舍五入的结果发生变化。
输入输出样例
示例
输入
5 2333
666 666 666 666 666
输出
0.0000#include
#include
#include
using namespace std;
long long n,s;
double a[500005];
double avg;
int main(){
cin>>n>>s;
for(int i=0;i>a[i];
}
avg=s*1.0/n;
sort(a,a+n);
double ans=0;
for(int i=0;i D:::::::::::::::最大子矩阵(线段树)
问题描述
小明有一个大小为 N×M 的矩阵, 可以理解为一个 N 行 M 列的二维数组。
我们定义一个矩阵 mm 的稳定度 f(m) 为 f(m)=max(m)−min(m), 其中 max(m) 表示矩阵 mm 中的最大值, min(m) 表示矩阵 m 中的最小值。
现在小明想要从这个矩阵中找到一个稳定度不大于 limit 的子矩阵, 同时他还希望这个子矩阵的面积越大越好 (面积可以理解为矩阵中元素个数)。
子矩阵定义如下: 从原矩阵中选择一组连续的行和一组连续的列, 这些行列交点上的元素组成的矩阵即为一个子矩阵。
输入格式
第一行输入两个整数 N,M, 表示矩阵的大小。
接下来 N 行, 侮行输入 M 个整数,表示这个矩阵。
最后一行输入一个整数 limit, 表示限制。
辎出格式
输出一个整数. 分别表示小明选择的子矩阵的最大面积。
样例输入
3 4
2 0 7 9
0 6 9 7
8 4 6 4
8
样例输出
6
样例说明
满足稳定度不大于 8 的且面积最大的子矩阵总共有三个, 他们的面积都是 6 (粗体表示子矩阵元素)
2 0 7 9
0 6 9 7
8 4 6 4
2 0 7 9
0 6 9 7
8 4 6 4
2 0 7 9
0 6 9 7
8 4 6 4
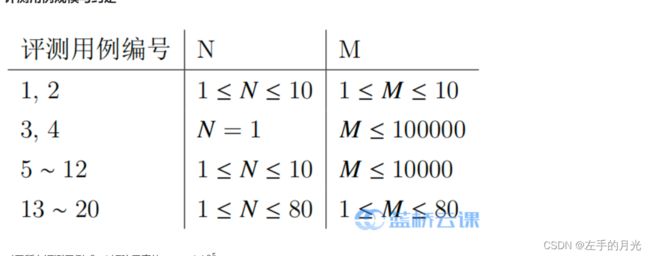
评测用例规模与约定
#include
using namespace std;
const int maxn = 1e5 + 7;
typedef long long ll;
const int mod = 998244353;
int a[101][maxn] , nowa[maxn] , nowi[maxn], n , m , k;
int ma[maxn << 2],mi[maxn << 2];
void build(int l , int r,int rt){
if(l == r){
ma[rt] = nowa[l];
mi[rt] = nowi[l];
return ;
}
int mid = (l + r) / 2;
build(l , mid , rt << 1);
build(mid + 1 , r , rt << 1 | 1);
ma[rt] = max(ma[rt << 1] , ma[rt << 1 | 1]);
mi[rt] = min(mi[rt << 1] , mi[rt << 1 | 1]);
}
int queryma(int L,int R,int l , int r,int rt){
int res = 0;
if(L <= l && R >= r){
return ma[rt];
}
int mid = (l + r) / 2;
if(L <= mid) res = max(res , queryma(L , R , l , mid , rt << 1));
if(R > mid) res = max(res , queryma(L , R , mid + 1 , r , rt << 1 | 1));
return res;
}
int querymi(int L,int R,int l , int r,int rt){
int res = 1e9;
if(L <= l && R >= r){
return mi[rt];
}
int mid = (l + r) / 2;
if(L <= mid) res = min(res , querymi(L , R , l , mid , rt << 1));
if(R > mid) res = min(res , querymi(L , R , mid + 1 , r , rt << 1 | 1));
return res;
}
int cal(int u , int d){
for(int i = 1; i <= m; i ++){
int ma = 0 , mi = 1e9;
for(int j = u; j <= d; j ++){
ma = max(ma , a[j][i]);
mi = min(mi , a[j][i]);
}
// printf ("%d %d\n",ma , mi);
nowa[i] = ma;nowi[i] = mi;
}
build(1 , m , 1);
int r = 1 , ans = 0;
// printf ("%d>>>>>>\n",queryma(1 , 1 , 1 , m ,1));
for(int l = 1; l <= m; l ++){
while(r <= m && queryma(l , r ,1 , m , 1) - querymi(l , r , 1 , m , 1) <= k){
r ++;
}
ans = max(ans , (d - u + 1) * (r - l));
// printf ("%d %d????\n",l , r);
}
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i ++){
for(int j = 1; j <= m; j ++){
scanf("%d",&a[i][j]);
}
}
scanf("%d",&k);
// printf ("%d\n",cal(1 , 3));
int ans = 0;
for(int i = 1; i <= n; i ++){
for(int j = i; j <= n; j ++){
ans = max(ans , cal(i , j));
}
}
printf ("%d\n",ans);
return 0;
} E:::::::::::::::跳跃(dp,dfs,bfs)
题目描述
小蓝在一个 n 行 m 列的方格图中玩一个游戏。
开始时,小蓝站在方格图的左上角,即第 1 行第 1 列。
小蓝可以在方格图上走动,走动时,如果当前在第 r 行第 c 列,他不能走到行号比 r 小的行,也不能走到列号比 c 小的列。同时,他一步走的直线距离不超过 3。
例如,如果当前小蓝在第 3 行第 5列,他下一步可以走到第 3 行第 6列、第 3 行第 7 列、第 3 行第 8 列、第 4 行第 5 列、第 4 行第 6列、第 4 行第 7 列、第 5 行第 5 列、第 5 行第 6 列、第 6 行第 5 列之一。
小蓝最终要走到第 n 行第 m 列。
在图中,有的位置有奖励,走上去即可获得,有的位置有惩罚,走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值,奖励为正,惩罚为负。
小蓝希望,从第 1 行第 1 列走到第 n 行第 m 列后,总的权值和最大。请问最大是多少?
输入描述
输入的第一行包含两个整数 n,m,表示图的大小。
接下来 n 行,每行 m 个整数,表示方格图中每个点的权值。
输出描述
输出一个整数,表示最大权值和。
输入输出样例
示例 1
输入
3 5
-4 -5 -10 -3 1
7 5 -9 3 -10
10 -2 6 -10 -4
输出
15dp解法:
#include
#include
#include
using namespace std;
int a[9][2]={{-1,0},{-2,0},{-3,0},{0,-1},{0,-2},{0,-3},{-1,-1},{-2,-1},{-1,-2}};
int n,m;
int b[105][105];
int dp[105][105];
bool check(int x,int y){
return x>=1&&x<=n&&y>=1&&y<=m;
}
int main(){
memset(b,-1e9,sizeof(b));
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>b[i][j];
}
}
dp[1][1]=b[1][1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int ans=0;
for(int v=0;v<9;v++){
int tx=i+a[v][0];
int ty=j+a[v][1];
if(check(tx,ty)){
dp[i][j]=max(dp[i][j],dp[tx][ty]+b[i][j]);
}
}
}
}
cout< dfs解法:
#include
#include
#include
using namespace std;
int a[9][2]={{1,0},{2,0},{3,0},{0,1},{0,2},{0,3},{1,1},{2,1},{1,2}};
int n,m;
int b[105][105];
bool c[105][105];
int res=-1e9;
bool check(int x,int y){
return x>=1&&x<=n&&y>=1&&y<=m;
}
void dfs(int x,int y,int ans){
if(x==n&&y==m){
res=max(ans,res);
return;
}
for(int i=0;i<9;i++){
int tx=x+a[i][0];
int ty=y+a[i][1];
if(check(tx,ty) && ! c[tx][ty]){
c[tx][ty]=1;
dfs(tx,ty,ans+b[tx][ty]);
c[tx][ty]=0;
}
}
}
int main(){
memset(b,-1e9,sizeof(b));
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>b[i][j];
}
}
dfs(1,1,b[1][1]);
cout< F:::::::::::::::蓝肽子序列(LCS最长公共子序列)
题目描述
L 星球上的生物由蛋蓝质组成,每一种蛋蓝质由一类称为蓝肽的物资首尾连接成一条长链后折叠而成。
生物学家小乔正在研究 L 星球上的蛋蓝质。她拿到两个蛋蓝质的蓝肽序列,想通过这两条蓝肽序列的共同特点来分析两种蛋蓝质的相似性。
具体的,一个蓝肽可以使用 1 至 5 个英文字母表示,其中第一个字母大写,后面的字母小写。一个蛋蓝质的蓝肽序列可以用蓝肽的表示顺序拼接而成。
在一条蓝肽序列中,如果选取其中的一些位置,把这些位置的蓝肽取出,并按照它们在原序列中的位置摆放,则称为这条蓝肽的一个子序列。蓝肽的子序列不一定在原序列中是连续的,中间可能间隔着一些未被取出的蓝肽。
如果第一条蓝肽序列可以取出一个子序列与第二条蓝肽序列中取出的某个子序列相等,则称为一个公共蓝肽子序列。
给定两条蓝肽序列,找出他们最长的那个公共蓝肽子序列的长度。
输入描述
输入两行,每行包含一个字符串,表示一个蓝肽序列。字符串中间没有空格等分隔字符。
其中有 ,两个字符串的长度均不超过 1000。
输出描述
输出一个整数,表示最长的那个公共蓝肽子序列的长度。
输入输出样例
示例
输入
LanQiaoBei
LanTaiXiaoQiao
输出
2#include
#include
using namespace std;
string a;
string b;
string a1[1005];
string b1[1005];
int dp[1005][1005];
int main(){
cin>>a>>b;
int len1=a.size();
int len2=b.size();
int len3=0,len4=0;
for(int i=0;i='A'){
len3++;
}
a1[len3]+=a[i];
}
for(int i=0;i='A'){
len4++;
}
b1[len4]+=b[i];
}
for(int i=1;i<=len3;i++){
for(int j=1;j<=len4;j++){
if(a1[i]==b1[j]){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
}
cout< G:::::::::::::::背包与魔法(01背包优化一维)
问题描述
小蓝面前有 N 件物品, 其中第 i 件重量是 Wi, 价值是 Vi 。她还有一个背包, 最大承重是 M 。
小蓝想知道在背包称重范围内, 她最多能装总价值多少的物品?
特别值得一提的是, 小蓝可以使用一个魔法 (总共使用一次), 将一件物品 的重量增加 K, 同时价值秝倍。(当然小蓝也可以不使用魔法)
输入格式
第一行包含 3 个整数 N、M 和 KK 。
以下 N 行, 每行两个整数 Wi 和 V_{i}Vi 。
输出格式
一个整数代表答案。
样例输入
3 10 3
5 10
4 9
3 8
样例输出
26
样例说明
选择第二件和第三件物品, 同时对第二件物品使用魔法。
#include
#include
using namespace std;
int n,m,k;
int wi[2005];
int vi[2005];
int dp[10010][2];
int main(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
cin>>wi[i]>>vi[i];
}
for(int i=1;i<=n;i++){
for(int j=m;j>=wi[i];j--){
dp[j][0]=max(dp[j][0],dp[j-wi[i]][0]+vi[i]);
if(j>=wi[i]+k){
dp[j][1]=max(dp[j][1],max(dp[j-wi[i]][1]+vi[i],dp[j-wi[i]-k][0]+vi[i]*2));
}
}
}
cout< 01背包模板:
#include
using namespace std;
const int N=1010;
int v[N],w[N],f[N];
int n,m;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d%d",&v[i],&w[i]);
for(int i=1;i<=n;i++)
for(int j=m;j>=v[i];j--)
{
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
printf("%d",f[m]);
return 0;
}
G:::::::::::::::本质上升序列(线性dp)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano等等。 小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个? 例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
#include
#include
using namespace std;
string a;
int dp[205];
int main(){
a="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
int len=a.size();
for(int i=0;ia[j]){
dp[i]+=dp[j];
}else if(a[i]==a[j]){
dp[i]=dp[i]-dp[j];
}
}
}
int ans=0;
for(int i=0;i H:::::::::::::::买不到的数目(悲蜀定理 dp)
题目描述
小明开了一家糖果店。他别出心裁:把水果糖包成 4 颗一包和 7 颗一包的两种。糖果不能拆包卖。
小朋友来买糖的时候,他就用这两种包装来组合。当然有些糖果数目是无法组合出来的,比如要买 10 颗糖。
你可以用计算机测试一下,在这种包装情况下,最大不能买到的数量是 17。大于 17 的任何数字都可以用 4 和 7 组合出来。
本题的要求就是在已知两个包装的数量时,求最大不能组合出的数字。
输入描述
输入两个正整数,表示每种包装中糖的颗数(都不多于 1000 )。
输出描述
输出一个正整数,表示最大不能买到的糖数。
不需要考虑无解的情况
输入输出样例
示例
输入
4 7
输出
17
运行限制
- 最大运行时间:3s
- 最大运行内存: 64M
悲蜀定理:
#inlcude
using namesapce std;
int a,b;
int main(){
cout<<(a-1)*(b-1)-1;
return 0;
} dp做法:
#include
using namespace std;
int a,b;
bool dp[1000005];
int ans;
int main() {
cin>>a>>b;
int c=a*b;
int xiao=min(a,b);
int da=max(a,b);
dp[da]=1;
dp[xiao]=1;
for(int i=1;i<=c;i++){
if(dp[i]){
dp[i+da]=1;
dp[i+xiao]=1;
}
}
for(int i=1;i I:::::::::::::::重复字符串(二维map)
题目描述
如果一个字符串 S 恰好可以由某个字符串重复 K 次得到,我们就称 S 是 K 次重复字符串。例如 abcabcabc 可以看作是 abc 重复 3 次得到,所以 abcabcabc 是 3 次重复字符串。
同理 aaaaaa 既是 2 次重复字符串、又是 3 次重复字符串和 6 次重复字符串。
现在给定一个字符串 S,请你计算最少要修改其中几个字符,可以使 S 变为一个 K 次字符串?
输入描述
输入第一行包含一个整数 K。
第二行包含一个只含小写字母的字符串 S。
其中,1≤K≤105,1≤∣S∣≤105。其中 ∣S∣ 表示 S 的 长度。
输出描述
输出一个整数代表答案。如果 S 无法修改成 K 次重复字符串,输出 −1。
输入输出样例
示例 1
输入
2
aabbaa
输出
2#include
#include
#include J:::::::::::::::回路计数(记忆化搜索)
题目描述
蓝桥学院由 21 栋教学楼组成,教学楼编号 1 到 21。对于两栋教学楼 a 和 b,当 a 和 b 互质时,a 和 b 之间有一条走廊直接相连,两个方向皆可通行,否则没有直接连接的走廊。
小蓝现在在第一栋教学楼,他想要访问每栋教学楼正好一次,最终回到第一栋教学楼(即走一条哈密尔顿回路),请问他有多少种不同的访问方案?
两个访问方案不同是指存在某个 i,小蓝在两个访问方法中访问完教学楼 i 后访问了不同的教学楼。
提示:建议使用计算机编程解决问题。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
#include
#include
#include
const int maxn=21;
const int maxs=1<>i)&1)==0)continue;
if(g[i][pos]==1){
dp[state-(1<