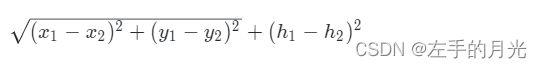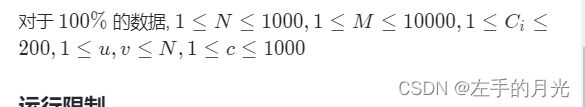带刷，带刷，刷起来！！！

A:::::::::::::::::::通电（最小生成树，Prim，Kruskal）

题目描述

2015 年，全中国实现了户户通电。作为一名电力建设者，小明正在帮助一带一路上的国家通电。

这一次，小明要帮助 n 个村庄通电，其中 1 号村庄正好可以建立一个发电站，所发的电足够所有村庄使用。

现在，这 n 个村庄之间都没有电线相连，小明主要要做的是架设电线连接这些村庄，使得所有村庄都直接或间接的与发电站相通。

小明测量了所有村庄的位置（坐标）和高度，如果要连接两个村庄，小明需要花费两个村庄之间的坐标距离加上高度差的平方，形式化描述为坐标为(x1​,y1​) 高度为 h1​ 的村庄与坐标为 (x2​,y2​) 高度为h2​ 的村庄之间连接的费用为

高度的计算方式与横纵坐标的计算方式不同。

由于经费有限，请帮助小明计算他至少要花费多少费用才能使这 n 个村庄都通电。

输入描述

输入的第一行包含一个整数 n ，表示村庄的数量。

接下来 n 行，每个三个整数 x,y,h，分别表示一个村庄的横、纵坐标和高度，其中第一个村庄可以建立发电站。

其中，1≤n≤1000，0≤x,y,h≤10000。

输出描述

输出一行，包含一个实数，四舍五入保留 2 位小数，表示答案。

输入输出样例

示例

输入

4
1 1 3
9 9 7
8 8 6
4 5 4

输出

17.41

#include 
#include 
#include 
#include 
using namespace std;
int n;
struct node{
	int x,y,h;
};
struct node1{
	int qi,zhong;
	double juli;
	node1(int qiqi,int zhongzhong,double julijuli){
		qi=qiqi;
		zhong=zhongzhong;
		juli=julijuli;
	}
};
int fa[10005];
int find(int x){
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}
bool panduan(int x,int y){
	int tx=find(x);
	int ty=find(y);
	if(tx==ty) return false;
	fa[tx]=ty;
	return true;
}
node dian[1005];
vector f;
bool cmp(node1 x,node1 y){
	return x.juli>n;
	for(int i=1;i<=n;i++){
		int x,y,h;
		cin>>x>>y>>h;
		dian[i].x=x;
		dian[i].y=y;
		dian[i].h=h; 
	}
	
	
	for(int i=1;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			double s= sqrt((dian[i].x-dian[j].x)*(dian[i].x-dian[j].x)+(dian[i].y-dian[j].y)*(dian[i].y-dian[j].y))+(dian[i].h-dian[j].h)*(dian[i].h-dian[j].h);
			f.push_back(node1(i,j,s));
		}
	}
	sort(f.begin(),f.end(),cmp);
	for(int i=1;i<=n;i++){
		fa[i]=i;
	}
	double ans=0;
	int len=f.size();
	for(int i=0;i

B:::::::::::::::::::正约数（唯一分解定理）

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

定义阶乘  n!=1×2×3×⋅⋅⋅×n。

请问 100! （100 的阶乘）有多少个正约数。

#include 
using namespace std;
int a[100];
long long ans=1;
int main(){

    for(int i=2;i<=100;i++){
        int n=i;
        for(int j=2;j<=n;j++){
            while(n%j==0 && n!=0){
                a[j]++;
                n=n/j;
            }
            
        }
    }
    for(int i=1;i<=100;i++){
        ans=(a[i]+1)*ans;
    }
    cout<

 C:::::::::::::::::::迷宫（BFS）

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可以通行的地方。

010000
000100
001001
110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这 个它的上、下、左、右四个方向之一。

对于上面的迷宫，从入口开始，可以按 DRRURRDDDR 的顺序通过迷宫， 一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫（30 行 50 列），请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。

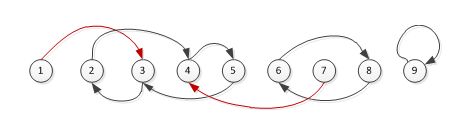
请注意在字典序中D

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

#include 
#include  
using namespace std;
char s[4]={'D','L','R','U'};
int b[4][2]={{1,0},{0,-1},{0,1},{-1,0}}; 

struct node{
    int x;
    int y;
    string a;
    int bushu;
    node(int xx,int yy,string aa,int aaa){
        x=xx;
        y=yy;
        a=aa;
        bushu=aaa;
    }
};
char a[35][55];
bool c[35][55];
queue q;
int guding;
void bfs(int xxx,int yyy){
    c[xxx][yyy]=1;
    q.push(node(xxx,yyy,"",0));
    while(!q.empty()){
        int xx=q.front().x;
        int yy=q.front().y;
        if(xx==29 && yy==49){
            cout<=0 && tx<30 && ty>=0 && ty<50 && !c[tx][ty] && a[tx][ty]=='0'){
        
                q.push(node(tx,ty,q.front().a+s[i],q.front().bushu++));
                c[tx][ty]=1;
            }
        }
        q.pop();
    }
}
int main(){
    for(int i=0;i<30;i++){
        for(int j=0;j<50;j++){
            cin>>a[i][j];
        }
    }
    bfs(0,0);           //(0,0)开始， 
    return 0;
}

  D:::::::::::::::::::发现环（并查集，DFS）

题目描述

小明的实验室有 N 台电脑，编号 1⋯N。原本这 N 台电脑之间有N−1 条数据链接相连，恰好构成一个树形网络。在树形网络上，任意两台电脑之间有唯一的路径相连。

不过在最近一次维护网络时，管理员误操作使得某两台电脑之间增加了一条数据链接，于是网络中出现了环路。环路上的电脑由于两两之间不再是只有一条路径，使得这些电脑上的数据传输出现了 BUG。

为了恢复正常传输。小明需要找到所有在环路上的电脑，你能帮助他吗？

输入描述

输入范围：

第一行包含一个整数 N 。

以下 N 行每行两个整数 a,b，表示 a 和 b 之间有一条数据链接相连。

其中， 1≤N≤105，1≤a,b≤N。

输入保证合法。

输出描述

按从小到大的顺序输出在环路上的电脑的编号，中间由一个空格分隔。

输入输出样例

示例

输入

5
1 2
3 1
2 4
2 5
5 3

输出

1 2 3 5

#include 
#include 
#include 
#include 
using namespace std;
int n;
int fa[100005];
bool vis[100005];
int find(int x){
	if(fa[x]==-1) return x;
	return fa[x]=find(fa[x]);
}
vector s[100005];

int qi,end1;
int flage;
bool pl;
int j[100005];
int mm=0;

void print(int step)
{
    sort(j+1,j+1+step);
    for(int i=1;i<=step;i++)
      cout<>n;
	memset(fa,-1,sizeof(fa));
	for(int i=0;i>a>>b;
	
		if(find(a)==find(b)){
			qi=a,end1=b;
		}else{
		fa[find(a)]=b;
      	s[a].push_back(b);
		s[b].push_back(a);
    }
	}
	dfs(qi,1);
	return 0;
}

  E:::::::::::::::::::大臣的旅费（双DFS）

题目描述

很久以前，T 王国空前繁荣。为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T 国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。

J 是 T 国重要大臣，他巡查于各大城市之间，体察民情。所以，从一个城市马不停蹄地到另一个城市成了 J 最常做的事情。他有一个钱袋，用于存放往来城市间的路费。

聪明的 J 发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第 x 千米到第 x +1 千米这一千米中（ x 是整数），他花费的路费是 x +10 这么多。也就是说走 1 千米花费 11，走 2 千米要花费 23。

J 大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入描述

输入的第一行包含一个整数 n，表示包括首都在内的 T 王国的城市数。

城市从 1 开始依次编号，1 号城市为首都。

接下来 n -1 行，描述 T 国的高速路（ T 国的高速路一定是 n -1 条）。

每行三个整数 Pi​,Qi​,Di​，表示城市 P_iPi​ 和城市 Qi​ 之间有一条高速路，长度为 Di​ 千米。

输出描述:

输出一个整数，表示大臣 J 最多花费的路费是多少。

输入输出样例

示例

输入

5
1 2 2
1 3 1
2 4 5
2 5 4

输出

135

样例说明

大臣 J 从城市 4 到城市 5 要花费 135 的路费。

 这道题好恶心，用dfs最后一个例题，数值较大，开足内存卡内存，不开内存，运行错误，用两遍dfs。

单个：80%

 

#include 
#include 
#include 
#include 
using namespace std;
int n;
int a[1010][1010];
vector g[10010];
int c;

bool vis[10010];
long long ans;
long long p;
void dfs(int qi,int zhong,long long bu){
	if(bu>ans){
		return;
	} 
	if(qi==zhong){
		ans=min(ans,bu);

		p=max(p,ans);
		return;
	}
	int len=g[qi].size();
	for(int i=0;i>n;
  if(n==1 || n==0){
    cout<<0;
    return 0;
  }
	for(int i=1;i>p>>q>>d;
		a[p][q]=a[q][p]=d; 
		g[p].push_back(q);
		g[q].push_back(p);
	}

	for(int i=1;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			ans=1e9;
			vis[i]=1;
			dfs(i,j,0);

			vis[i]=0;
			c++;
		}
	}

	cout<

两遍：

#include 
#include
using namespace std;
const int N =100010;

int n;
struct Edge
{
  int id,w;
};
vector h[N];
int dist[N];

void dfs(int u,int father,int distance)
{
  dist[u] = distance;

  for(auto node : h[u])   
    if(node.id!= father)   
      dfs(node.id,u,distance + node.w);
}

int main()
{
  scanf("%d",&n);
  for(int i=0;idist[u]) u=i;


  dfs(u,-1,0);

  for(int i=1;i<=n;i++)
    if(dist[i]>dist[u]) u=i;
 int v = dist[u];


printf("%lld\n",10*v + v*(v+1ll)/2);
  return 0;
}

  F:::::::::::::::::::最小公倍数（高精度）

题目描述

为什么 1 小时有 60 分钟，而不是 100 分钟呢？这是历史上的习惯导致。

但也并非纯粹的偶然：60 是个优秀的数字，它的因子比较多。

事实上，它是 1 至 6 的每个数字的倍数。即 1,2,3,4,5,6 都是可以除尽 60。

我们希望寻找到能除尽 1 至 n 的的每个数字的最小整数。

不要小看这个数字，它可能十分大，比如 n = 100, 则该数为：

69720375229712477164533808935312303556800

输入描述

输入一个数字 (N<100)。

输出描述

输出出 1 ~ nn 的最小公倍数。

输入输出样例

示例

输入

6

输出

 

60

 #include
#include
using namespace std;
int prime[101],ans=0;
void prime_it(){
    for(int i=1;i<=100;i++)prime[i]=i;
    for(int i=2;i<=100;i++){
        for(int j=2;j<=i-1;j++)if(prime[i]%prime[j]==0)prime[i]/=prime[j];
    }
}
int num[101],len=1;
int main(){
    int n;
    prime_it();
    while(cin>>n){
        memset(num,0,sizeof(num));
        num[1]=1,len=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=len;j++){
                num[j]*=prime[i];
            }
            for(int j=1;j<=len;j++){
                num[j+1]+=num[j]/10;
                num[j]%=10;
            }
            while(num[len+1]){
                len++;
                num[len+1]=num[len]/10;
                num[len]%=10;
            }
        }
        for(int i=len;i>=1;i--)cout<

   G:::::::::::::::::::排列叙述（全排列）

题目描述

如果用 a b c d 这 4 个字母组成一个串，有 4!=24 种，如果把它们排个序，每个串都对应一个序号：

abcd 0

abdc 1

acbd 2

acdb 3

adbc 4

adcb 5

bacd 6

badc 7

bcad 8

bcda 9

bdac 10

bdca 11

cabd 12

cadb 13

cbad 14

cbda 15

cdab 16

cdba 17

⋯

现在有不多于 10 个两两不同的小写字母，给出它们组成的串，你能求出该串在所有排列中的序号吗？

输入描述

输入一行，一个串。

输出描述

输出一行，一个整数，表示该串在其字母所有排列生成的串中的序号。注意：最小的序号是 0。

输入输出样例

示例

输入

bdca

输出

11

 

#include 
#include 
#include 
using namespace std;
string arr;
long long ans=0;
int main(){
	cin>>arr;
	string arr1=arr;
	sort(arr1.begin(),arr1.end());
	if(arr1==arr){
		cout<<0;
		return 0;
	}
	while(next_permutation(arr1.begin(),arr1.end())){
		if(arr1==arr){
			break;
		}
		ans++;
	}
	cout<

   H:::::::::::::::::::小朋友崇拜圈（DFS）

题目描述

班里 NN 个小朋友，每个人都有自己最崇拜的一个小朋友（也可以是自己）。

在一个游戏中，需要小朋友坐一个圈，每个小朋友都有自己最崇拜的小朋友在他的右手边。

求满足条件的圈最大多少人？

小朋友编号为 1,2,3,⋯N。

输入描述

输入第一行，一个整数 N（3

接下来一行 N 个整数，由空格分开。

输出描述

要求输出一个整数，表示满足条件的最大圈的人数。

输入输出样例

示例

输入

9
3 4 2 5 3 8 4 6 9

输出

4

样例解释

如下图所示，崇拜关系用箭头表示，红色表示不在圈中。

显然，最大圈是[2 4 5 3] 构成的圈。

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

#include 
using namespace std;
int a[300005];
bool vis[300005];
int n;
bool p;
int ans;
void dfs(int x,int y,int an){
	if(x==y && an>1){
		ans=max(ans,an);
		return;
	}
	if(!vis[x]){
		vis[x]=1;
		dfs(a[x],y,an+1);
		vis[x]=0;
	}
	
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<=n;i++){
			p=false;
			dfs(i,i,0);
	} 
	cout<

   I:::::::::::::::::::出差（Dijkstra）

问题描述

A 国有 N 个城市, 编号为 1…N 。小明是编号为 1 的城市中一家公司的员 工, 今天突然接到了上级通知需要去编号为 N 的城市出差。

由于疫情原因, 很多直达的交通方式暂时关闭, 小明无法乘坐飞机直接从 城市 1 到达城市 N, 需要通过其他城市进行陆路交通中转。小明通过交通信息 网, 查询到了M 条城市之间仍然还开通的路线信息以及每一条路线需要花费的 时间。

同样由于疫情原因, 小明到达一个城市后需要隔离观察一段时间才能离开 该城市前往其他城市。通过网络, 小明也查询到了各个城市的隔离信息。(由于 小明之前在城市 1 , 因此可以直接离开城市 1 , 不需要隔离）

由于上级要求, 小明希望能够尽快赶到城市 N, 因此他求助于你, 希望你 能帮他规划一条路线, 能够在最短时间内到达城市 N 。

输入格式

第 1 行: 两个正整数 N,M,N 表示 A 国的城市数量, M 表示末关闭的路 线数量

第 2 行: N 个正整数, 第 i 个整数 Ci​ 表示到达编号为 i 的城市后需要隔离 的时间

第 3…M+2 行: 每行 3 个正整数,u,v,c, 表示有一条城市 u 到城市 v 的 双向路线仍然开通着, 通过该路线的时间为 c

输出格式

第 1 行: 1 个正整数, 表示小明从城市 1 出发到达城市 N 的最短时间（到 达城市 N, 不需要计算城市 N 的隔离时间）

样例输入

4 4
5 7 3 4
1 2 4
1 3 5
2 4 3
3 4 5

样例输出

13

样例说明

评测用例规模与约定

 

运行限制

• 最大运行时间：1s
• 最大运行内存: 512M

#include 
#include 
#include 
using namespace std;
int n,m;     //n个城市，m条路线 
int geli[10005];   //到每个城市的隔离时间 
int luxian[10005][10005];
int juli[10005];          //到一点的最短距离 
bool vis[10005];
int dj(){
    memset(juli,0x3f3f3f3f,sizeof(juli));
    juli[1]=0;      //距离起点为0 
    geli[1]=0;      //出自己城市不隔离 
    geli[n]=0;      //到达终点不需要隔离 
    for(int i=1;i<=n;i++){
        int s=-1;
        for(int j=1;j<=n;j++){
            if(!vis[j]&&((s==-1)||(juli[j]>n>>m;
    for(int i=1;i<=n;i++){
        cin>>geli[i];
    }
    memset(luxian,0x3f3f3f3f,sizeof(luxian));  //无穷大
    for(int i=1;i<=n;i++){
        luxian[i][i]=0;                    //自己到自己为0 
    } 
    for(int i=0;i>a>>b>>c;
        luxian[a][b]=luxian[b][a]=min(c,luxian[a][b]);
    }
    int ans=dj(); 
    cout<

    J:::::::::::::::::::百亿富翁（单调栈）

题目描述

这天小明买彩票中了百亿奖金，兴奋的他决定买下蓝桥公司旁的一排连续的楼房。

已知这排楼房一共有 N 栋，编号分别为 1∼N，第 ii 栋的高度为 hi​。

好奇的小明想知道对于每栋楼，左边第一个比它高的楼房是哪个，右边第一个比它高的楼房是哪个（若不存在则输出 −1）。但由于楼房数量太多，小明无法用肉眼直接得到答案，于是他花了 1 个亿来请你帮他解决问题，你不会拒绝的对吧？

输入描述

第 1 行输入一个整数 N，表示楼房的数量。

第 2 行输入 N 个整数（相邻整数用空格隔开），分别为h1​,h2​,...,hN​，表示楼房的高度。

1≤N≤7×105，1≤hi​≤109。

输出描述

输出共两行。

第一行输出 N 个整数，表示每栋楼左边第一栋比自己高的楼的编号。

第二行输出 N 个整数，表示每栋楼右边第一栋比自己高的楼的编号。

输入输出样例

示例 1

输入

5
3 1 2 5 4 

输出

-1 1 1 -1 4
4 3 4 -1 -1

 

 

#include 
#include 
using namespace std;
int n;
long long a[700005];
stack st;
int l[700005];
int r[700005];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int i=1;i<=n;i++){
		while(st.size() && a[st.top()]<=a[i]) st.pop();
		if(st.size()){
			l[i]=st.top();
		}else{
			
			l[i]=-1;
		}
		st.push(i);
	}

	while(!st.empty()){
		st.pop();
	}
	
	for(int i=n;i>=1;i--){
		while(st.size() && a[st.top()]<=a[i]) st.pop();
		if(st.size()){
			r[i]=st.top();
		}else{
			r[i]=-1;
		}
		st.push(i);
	}
	for(int i=1;i<=n;i++){
		cout<