【图论】图的定义和术语

本文为图论总结，介绍基本的图的定义和术语及简单定理。

基本术语

序列中顶点不重复出现的路径称为简单路径。

顶点 $v$ 的所有相邻顶点集合记作 $N(v)$。

将度为 0 的顶点称为孤立的，度为 1 度顶点称为悬挂的。入度记作 ${\mathrm{deg}}^{-}(v)$，出度记作 ${\mathrm{deg}}^{+}(v)$。

对于有向图，忽略有向边后得到的无向图称为基本无向图。

握手定理

设 $G=(V,E)$ 是有 $m$ 条边的无向图则：
$$2m=\sum _{v\in V}\mathrm{deg}(v)$$
即使出现多重边和环，上式依然成立。直观解释是：每条边贡献 2 个度。

有向图的握手定理：
$$\sum _{v\in V}{\mathrm{deg}}^{-}(v)=\sum _{v\in V}{\mathrm{deg}}^{+}(v)=|E|$$

连通图

如果任意两个顶点都是连通的，则图称为连通图

连通分量指的是无向图中的极大连通子图

有向图中，如果每对顶点间都存在路径，则称为强连通图。有向图中的极大连通子图称作有向图的强连通分量

一个连通图的生成树是极小连通子图，其含有图中全部顶点，但只有足以构成树的 $n-1$ 条边。如果在生成树上加一条边，必定构成一个环。

如果一个图有 $n$ 个顶点和小于 $n-1$ 条边，则是非连通图。如果多于 $n-1$ 条边，则一定有环。

如果恰有一个顶点的入度为 0，其余顶点的入度均为 1，则是一颗有向树。

特殊的简单图

完全图

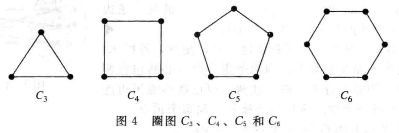
圈图

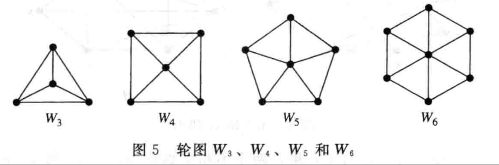
轮图

$n$ 立方体

二分图

将简单图 $G$ 的顶点集分成两个不相交的非空集合 $V_1,V_2$，使得图中每一条边都各连接 $V_1,V_2$ 中的一个顶点（即两个非空子集内部顶点间没有边），则 $G$ 称为二分图，称 $(V_1,V_2)$ 为 $G$ 的顶点集的一个二部划分。

判断一个简单图是否为二分图的准则：一个简单图为二分图，当且仅当能够对图中每个顶点赋予两种不同的颜色，并使得没有两个相邻的顶点被赋予相同的颜色。

完全二分图 $K_{m,n}$ 是顶点集划分成分别含有 $m$ 和 $n$ 个顶点的两个子集的图，并且两个顶点之间有边当且仅当两个顶点属于不同的子集。

二分图和匹配

类似于给员工分配工作的问题，每个工作只能分配给一个员工，每个员工只能执行一个工作。匹配 $M$ 就是图中边集 $E$ 的子集，该子集没有两条关联相同的顶点。包含边数最多的匹配称为最大匹配。

若 $|M|=|V_1|$，则称 $M$ 是从 $V_1$ 到 $V_2$ 的完全匹配。霍尔婚姻定理给出了完全匹配的充要条件。

带有二部划分 $(V_1,V_2)$ 的二分图 $G=(V,E)$ 中有一个从 $V_1$ 到 $V_2$ 的完全匹配当且仅当对于 $V_1$ 的所有子集 $A$，有 $|N(A)|\ge |A|$。直观解释是，在每个小区域内 $A$ 的领域个数多余 $A$ 集合中顶点个数，即每个小区域内 $A$ 中顶点都能完全匹配。

从旧图构造新图

子图：从图中删除边和顶点，不删除保留边的端点。子图与原图不相等时称为真子图。

导出的子图：只删除点及其连接的点生成出的子图。

边的收缩：删除端点为 $u,v$ 的边 $e$，把 $u,v$ 合并为新的顶点 $w$，对应边也进行合并。

图的并集：顶点和边集同时取并集

有帮助的话点个赞和关注吧