Removing the bias of integral pose regression阅读笔记
这里只写了Removing the bias of integral pose regression方法和自己实现的代码
H ( p ) \mathbf{H}\left(\mathbf{p}\right) H(p)表示热力图
H ~ ( p ) = exp ( β ⋅ H ( p ) ) ∑ p ′ ∈ Ω exp ( β ⋅ H ( p ′ ) ) , β > 0 \tilde{\mathbf{H}}(\mathbf{p})=\frac{\exp (\beta \cdot \mathbf{H}(\mathbf{p}))}{\sum_{\mathbf{p}^{\prime} \in \Omega} \exp \left(\beta \cdot \mathbf{H}\left(\mathbf{p}^{\prime}\right)\right)}, \quad \beta>0 H~(p)=∑p′∈Ωexp(β⋅H(p′))exp(β⋅H(p)),β>0
其中 Ω \Omega Ω表示整张图的坐标
C = ∑ p ′ ∈ Ω exp ( β ⋅ H ( p ′ ) ) C=\sum_{\mathbf{p}^{\prime} \in \Omega} \exp \left(\beta \cdot \mathbf{H}\left(\mathbf{p}^{\prime}\right)\right) C=p′∈Ω∑exp(β⋅H(p′))
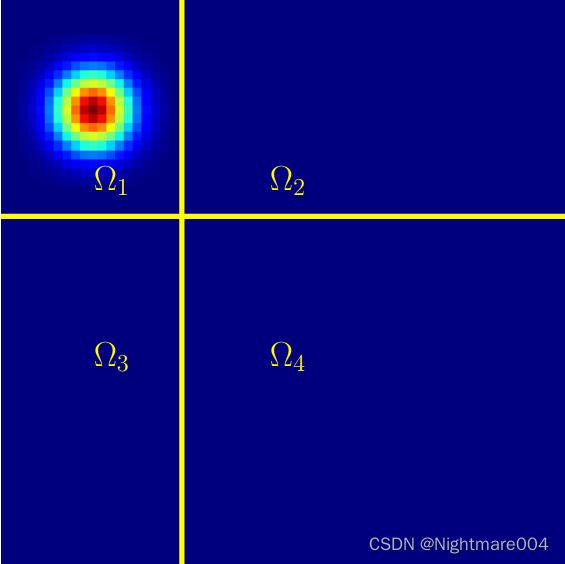
其中 Ω 1 , Ω 2 , Ω 3 , Ω 4 \Omega_1, \Omega_2, \Omega_3, \Omega_4 Ω1,Ω2,Ω3,Ω4 分别表示左上,右上,左下,右下
( x 0 , y 0 ) \left(x_0, y_0\right) (x0,y0)是没有偏差的坐标
J r = ( x r y r ) = ∑ p ∈ Ω H ~ ( p ) ⋅ p \mathbf{J}^r = \begin{pmatrix} x_r\\ y_r \end{pmatrix} = \sum_{\mathbf{p} \in \Omega} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p} Jr=(xryr)=p∈Ω∑H~(p)⋅p
J r o = ( x 0 y 0 ) = C C − h w J r − ( h 2 w 2 ( C − h w ) h w 2 2 ( C − h w ) ) \mathbf{J}^{r o}=\begin{pmatrix} x_0 \\ y_0 \end{pmatrix}=\frac{C}{C-hw}\mathbf{J}^r -\begin{pmatrix} \frac{h^2 w}{2(C-h w)} \\ \frac{h w^2}{2(C-h w)} \end{pmatrix} Jro=(x0y0)=C−hwCJr−(2(C−hw)h2w2(C−hw)hw2)
(不过论文里是 J r o = ( x 0 y 0 ) = C C − h w J r − ( h w 2 2 ( C − h w ) h 2 w 2 ( C − h w ) ) \mathbf{J}^{r o}=\begin{pmatrix} x_0 \\ y_0 \end{pmatrix}=\frac{C}{C-hw}\mathbf{J}^r -\begin{pmatrix} \frac{h w^2}{2(C-h w)} \\ \frac{h^2 w}{2(C-h w)} \end{pmatrix} Jro=(x0y0)=C−hwCJr−(2(C−hw)hw22(C−hw)h2w),不知道为什么)
推导
左上
以 2 x 0 , 2 y 0 2x_0,2y_0 2x0,2y0将整张图划分为4个区域

由于其他地方的值比较接近于0,所以热力图可以近似表示为
H ~ ( p ) ≈ { exp ( β ⋅ H ( p ) ) C , p ∈ Ω 1 1 C , p ∉ Ω 1 \tilde{\mathbf{H}} \left(p\right) \approx \begin{cases} \frac{\exp (\beta \cdot \mathbf{H}(\mathbf{p}))}{C},& p\in \Omega_1\\ \frac{1}{C},& p\not\in \Omega_1 \end{cases} H~(p)≈{Cexp(β⋅H(p)),C1,p∈Ω1p∈Ω1
因此
J r = ∑ p ∈ Ω H ~ ( p ) ⋅ p = ∑ p ∈ Ω 1 H ~ ( p ) ⋅ p + ∑ p ∈ Ω 2 , Ω 3 , Ω 4 H ~ ( p ) ⋅ p = w 1 J 1 + w 2 J 2 + w 3 J 3 + w 4 J 4 \begin{aligned} \mathbf{J}^r & =\sum_{\mathbf{p} \in \Omega} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p} \\ & =\sum_{\mathbf{p} \in \Omega_1} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}+\sum_{\mathbf{p} \in \Omega_2, \Omega_3, \Omega_4} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}\\ &= w_1 \mathbf{J}_1 + w_2 \mathbf{J}_2 + w_3 \mathbf{J}_3 + w_4 \mathbf{J}_4 \end{aligned} Jr=p∈Ω∑H~(p)⋅p=p∈Ω1∑H~(p)⋅p+p∈Ω2,Ω3,Ω4∑H~(p)⋅p=w1J1+w2J2+w3J3+w4J4
其中每个区域的中心点坐标为
J 1 = ( x 0 y 0 ) J 2 = ( x 0 2 y 0 + w − 2 y 0 2 ) = ( x 0 y 0 + w 2 ) J 3 = ( 2 x 0 + h − 2 x 0 2 y 0 ) = ( x 0 + h 2 y 0 ) J 4 = ( x 0 + h 2 y 0 + w 2 ) \mathbf{J}_1 = \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix}\\ \mathbf{J}_2 = \begin{pmatrix} x_0\\ 2y_0 + \frac{w - 2y_0}{2}\\ \end{pmatrix} = \begin{pmatrix} x_0\\ y_0 + \frac{w}{2}\\ \end{pmatrix}\\ \mathbf{J}_3 = \begin{pmatrix} 2x_0 + \frac{h - 2 x_0}{2}\\ y_0\\ \end{pmatrix} = \begin{pmatrix} x_0 + \frac{h}{2} \\ y_0\\ \end{pmatrix}\\ \mathbf{J}_4 = \begin{pmatrix} x_0 + \frac{h}{2}\\ y_0 + \frac{w}{2}\\ \end{pmatrix} J1=(x0y0)J2=(x02y0+2w−2y0)=(x0y0+2w)J3=(2x0+2h−2x0y0)=(x0+2hy0)J4=(x0+2hy0+2w)
权重
w 2 = 2 x 0 ( w − 2 y 0 ) C w 3 = 2 ( h − 2 x 0 ) y 0 C w 4 = ( h − 2 x 0 ) ( w − 2 y 0 ) C w 1 = 1 − w 2 − w 3 − w 4 w_2 = \frac{2x_0\left(w - 2y_0\right)}{C}\\ w_3 = \frac{2\left(h - 2x_0\right)y_0}{C}\\ w_4 = \frac{\left(h - 2x_0\right)\left(w - 2y_0\right)}{C}\\ w_1 = 1 - w_2 - w_3 - w_4 w2=C2x0(w−2y0)w3=C2(h−2x0)y0w4=C(h−2x0)(w−2y0)w1=1−w2−w3−w4
(计算方法就是区域的像素个数乘 1 C \frac{1}{C} C1
因此
J r = ( w 1 x 0 + w 2 x 0 + w 3 ( x 0 + h 2 ) + w 4 ( x 0 + h 2 ) w 1 y 0 + w 2 ( y 0 + w 2 ) + w 3 y 0 + w 4 ( y 0 + w 2 ) ) = ( x 0 + ( w 3 + w 4 ) h 2 y 0 + ( w 2 + w 4 ) w 2 ) = ( ( 1 − h w C ) x 0 + h w C h 2 ( 1 − h w C ) y 0 + h w C w 2 ) \begin{aligned} \mathbf{J}^r &= \begin{pmatrix} w_1 x_0 + w_2 x_0 + w_3 \left(x_0 + \frac{h}{2}\right) + w_4\left(x_0 + \frac{h}{2}\right)\\ w_1 y_0 + w_2 \left(y_0 + \frac{w}{2}\right) + w_3 y_0 + w_4\left(y_0 + \frac{w}{2}\right)\\ \end{pmatrix}\\ &= \begin{pmatrix} x_0 + \left(w_3 + w_4\right)\frac{h}{2}\\ y_0 + \left(w_2 + w_4\right)\frac{w}{2}\\ \end{pmatrix}\\ &=\begin{pmatrix} \left(1-\frac{h w}{C}\right) x_0+\frac{h w}{C} \frac{h}{2}\\ \left(1-\frac{h w}{C}\right) y_0+\frac{h w}{C} \frac{w}{2} \end{pmatrix} \end{aligned} Jr=(w1x0+w2x0+w3(x0+2h)+w4(x0+2h)w1y0+w2(y0+2w)+w3y0+w4(y0+2w))=(x0+(w3+w4)2hy0+(w2+w4)2w)=((1−Chw)x0+Chw2h(1−Chw)y0+Chw2w)
可以解出来
J r o = ( x 0 y 0 ) = ( C C − h w x r − h 2 w 2 ( C − h w ) C C − h w y r − h w 2 2 ( C − h w ) ) \mathbf{J}^{r o}=\begin{pmatrix} x_0 \\ y_0 \end{pmatrix}=\begin{pmatrix} \frac{C}{C-h w} x_r-\frac{h^2 w}{2(C-h w)} \\ \frac{C}{C-h w} y_r-\frac{h w^2}{2(C-h w)} \end{pmatrix} Jro=(x0y0)=(C−hwCxr−2(C−hw)h2wC−hwCyr−2(C−hw)hw2)
右上
以 2 x 0 , 2 ( w − y 0 ) 2x_0,2(w-y_0) 2x0,2(w−y0)将整张图划分为4个区域

由于其他地方的值比较接近于0,所以热力图可以近似表示为
H ~ ( p ) ≈ { exp ( β ⋅ H ( p ) ) C , p ∈ Ω 2 1 C , p ∉ Ω 2 \tilde{\mathbf{H}} \left(p\right) \approx \begin{cases} \frac{\exp (\beta \cdot \mathbf{H}(\mathbf{p}))}{C},& p\in \Omega_2\\ \frac{1}{C},& p\not\in \Omega_2 \end{cases} H~(p)≈{Cexp(β⋅H(p)),C1,p∈Ω2p∈Ω2
因此
J r = ∑ p ∈ Ω H ~ ( p ) ⋅ p = ∑ p ∈ Ω 2 H ~ ( p ) ⋅ p + ∑ p ∈ Ω 1 , Ω 3 , Ω 4 H ~ ( p ) ⋅ p = w 2 J 2 + w 1 J 1 + w 3 J 3 + w 4 J 4 \begin{aligned} \mathbf{J}^r & =\sum_{\mathbf{p} \in \Omega} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p} \\ & =\sum_{\mathbf{p} \in \Omega_2} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}+\sum_{\mathbf{p} \in \Omega_1, \Omega_3, \Omega_4} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}\\ &= w_2 \mathbf{J}_2 + w_1 \mathbf{J}_1 + w_3 \mathbf{J}_3 + w_4 \mathbf{J}_4 \end{aligned} Jr=p∈Ω∑H~(p)⋅p=p∈Ω2∑H~(p)⋅p+p∈Ω1,Ω3,Ω4∑H~(p)⋅p=w2J2+w1J1+w3J3+w4J4
其中每个区域的中心点坐标为
J 1 = ( x 0 w − 2 ( w − y 0 ) 2 ) = ( x 0 y 0 − w 2 ) J 2 = ( x 0 y 0 ) J 3 = ( 2 x 0 + h − 2 x 0 2 w − 2 ( w − y 0 ) 2 ) = ( x 0 + h 2 y 0 − w 2 ) J 4 = ( x 0 + h 2 y 0 ) \mathbf{J}_1 = \begin{pmatrix} x_0\\ \frac{w - 2\left(w - y_0\right)}{2}\\ \end{pmatrix} = \begin{pmatrix} x_0\\ y_0-\frac{w}{2}\\ \end{pmatrix}\\ \mathbf{J}_2 = \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix}\\ \mathbf{J}_3 = \begin{pmatrix} 2x_0 + \frac{h - 2x_0}{2}\\ \frac{w - 2\left(w - y_0\right)}{2}\\ \end{pmatrix} = \begin{pmatrix} x_0 + \frac{h}{2}\\ y_0-\frac{w}{2}\\ \end{pmatrix}\\ \mathbf{J}_4 = \begin{pmatrix} x_0 + \frac{h}{2}\\ y_0\\ \end{pmatrix} J1=(x02w−2(w−y0))=(x0y0−2w)J2=(x0y0)J3=(2x0+2h−2x02w−2(w−y0))=(x0+2hy0−2w)J4=(x0+2hy0)
权重
w 1 = 2 x 0 ( 2 y 0 − w ) C w 3 = ( h − 2 x 0 ) ( 2 y 0 − w ) C w 4 = 2 ( h − 2 x 0 ) ( w − y 0 ) C w 2 = 1 − w 1 − w 3 − w 4 w_1 = \frac{2x_0\left(2y_0-w\right)}{C}\\ w_3 = \frac{\left(h - 2x_0\right)\left(2y_0 - w\right)}{C}\\ w_4 = \frac{2\left(h - 2x_0\right)\left(w - y_0\right)}{C}\\ w_2 = 1 - w_1 - w_3 - w_4 w1=C2x0(2y0−w)w3=C(h−2x0)(2y0−w)w4=C2(h−2x0)(w−y0)w2=1−w1−w3−w4
(计算方法就是区域的像素个数乘 1 C \frac{1}{C} C1
因此
J r = ( w 1 x 0 + w 2 x 0 + w 3 ( x 0 + h 2 ) + w 4 ( x 0 + h 2 ) w 1 ( y 0 − w 2 ) + w 2 y 0 + w 3 ( y 0 − w 2 ) + w 4 y 0 ) = ( x 0 + ( w 3 + w 4 ) h 2 y 0 − ( w 1 + w 3 ) w 2 ) = ( ( 1 − h w C ) x 0 + h w C h 2 ( 1 − h w C ) y 0 + h w C w 2 ) \begin{aligned} \mathbf{J}^r &= \begin{pmatrix} w_1 x_0 + w_2 x_0 + w_3 \left(x_0 + \frac{h}{2}\right) + w_4\left(x_0 + \frac{h}{2}\right)\\ w_1 \left(y_0 - \frac{w}{2}\right) + w_2 y_0 + w_3 \left(y_0 - \frac{w}{2}\right) + w_4y_0\\ \end{pmatrix}\\ &= \begin{pmatrix} x_0 + \left(w_3 + w_4\right)\frac{h}{2}\\ y_0 - \left(w_1 + w_3\right)\frac{w}{2}\\ \end{pmatrix}\\ &=\begin{pmatrix} \left(1-\frac{h w}{C}\right) x_0+\frac{h w}{C} \frac{h}{2}\\ \left(1-\frac{h w}{C}\right) y_0+\frac{h w}{C} \frac{w}{2} \end{pmatrix} \end{aligned} Jr=(w1x0+w2x0+w3(x0+2h)+w4(x0+2h)w1(y0−2w)+w2y0+w3(y0−2w)+w4y0)=(x0+(w3+w4)2hy0−(w1+w3)2w)=((1−Chw)x0+Chw2h(1−Chw)y0+Chw2w)
可以解出来
J r o = ( x 0 y 0 ) = ( C C − h w x r − h 2 w 2 ( C − h w ) C C − h w y r − h w 2 2 ( C − h w ) ) \mathbf{J}^{r o}=\begin{pmatrix} x_0 \\ y_0 \end{pmatrix}=\begin{pmatrix} \frac{C}{C-h w} x_r-\frac{h^2 w}{2(C-h w)} \\ \frac{C}{C-h w} y_r-\frac{h w^2}{2(C-h w)} \end{pmatrix} Jro=(x0y0)=(C−hwCxr−2(C−hw)h2wC−hwCyr−2(C−hw)hw2)
左下
以 2 ( h − x 0 ) , 2 y 0 2(h - x_0),2y_0 2(h−x0),2y0将整张图划分为4个区域
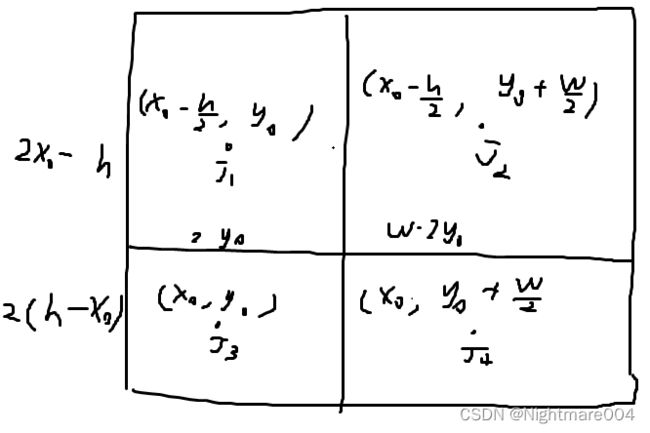
由于其他地方的值比较接近于0,所以热力图可以近似表示为
H ~ ( p ) ≈ { exp ( β ⋅ H ( p ) ) C , p ∈ Ω 3 1 C , p ∉ Ω 3 \tilde{\mathbf{H}} \left(p\right) \approx \begin{cases} \frac{\exp (\beta \cdot \mathbf{H}(\mathbf{p}))}{C},& p\in \Omega_3\\ \frac{1}{C},& p\not\in \Omega_3 \end{cases} H~(p)≈{Cexp(β⋅H(p)),C1,p∈Ω3p∈Ω3
因此
J r = ∑ p ∈ Ω H ~ ( p ) ⋅ p = ∑ p ∈ Ω 3 H ~ ( p ) ⋅ p + ∑ p ∈ Ω 1 , Ω 2 , Ω 4 H ~ ( p ) ⋅ p = w 3 J 3 + w 1 J 1 + w 2 J 2 + w 4 J 4 \begin{aligned} \mathbf{J}^r & =\sum_{\mathbf{p} \in \Omega} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p} \\ & =\sum_{\mathbf{p} \in \Omega_3} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}+\sum_{\mathbf{p} \in \Omega_1, \Omega_2, \Omega_4} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}\\ &= w_3 \mathbf{J}_3 + w_1 \mathbf{J}_1 + w_2 \mathbf{J}_2 + w_4 \mathbf{J}_4 \end{aligned} Jr=p∈Ω∑H~(p)⋅p=p∈Ω3∑H~(p)⋅p+p∈Ω1,Ω2,Ω4∑H~(p)⋅p=w3J3+w1J1+w2J2+w4J4
其中每个区域的中心点坐标为
J 1 = ( h − 2 ( h − x 0 ) 2 y 0 ) = ( x 0 − h 2 y 0 ) J 2 = ( x 0 − h 2 2 y 0 + w − 2 y 0 2 ) = ( x 0 − h 2 y 0 + w 2 ) J 3 = ( x 0 y 0 ) J 4 = ( x 0 y 0 + w 2 ) \mathbf{J}_1 = \begin{pmatrix} \frac{h - 2(h-x_0)}{2}\\ y_0\\ \end{pmatrix}= \begin{pmatrix} x_0 - \frac{h}{2}\\ y_0\\ \end{pmatrix} \\ \mathbf{J}_2 = \begin{pmatrix} x_0 - \frac{h}{2}\\ 2y_0 + \frac{w - 2y_0}{2}\\ \end{pmatrix}= \begin{pmatrix} x_0 - \frac{h}{2}\\ y_0 + \frac{w}{2}\\ \end{pmatrix}\\ \mathbf{J}_3 = \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix}\\ \mathbf{J}_4 = \begin{pmatrix} x_0\\ y_0 + \frac{w}{2}\\ \end{pmatrix} J1=(2h−2(h−x0)y0)=(x0−2hy0)J2=(x0−2h2y0+2w−2y0)=(x0−2hy0+2w)J3=(x0y0)J4=(x0y0+2w)
权重
w 1 = 2 ( 2 x 0 − h ) y 0 C w 2 = ( 2 x 0 − h ) ( w − 2 y 0 ) C w 4 = 2 ( h − x 0 ) ( w − 2 y 0 ) C w 3 = 1 − w 1 − w 2 − w 4 w_1 = \frac{2\left(2x_0 - h\right)y_0}{C}\\ w_2 = \frac{\left(2x_0 - h\right)\left(w - 2y_0\right)}{C}\\ w_4 = \frac{2\left(h - x_0\right)\left(w - 2y_0\right)}{C}\\ w_3 = 1 - w_1 - w_2 - w_4 w1=C2(2x0−h)y0w2=C(2x0−h)(w−2y0)w4=C2(h−x0)(w−2y0)w3=1−w1−w2−w4
(计算方法就是区域的像素个数乘 1 C \frac{1}{C} C1
因此
J r = ( w 1 ( x 0 − h 2 ) + w 2 ( x 0 − h 2 ) + w 3 x 0 + w 4 x 0 w 1 y 0 + w 2 ( y 0 + w 2 ) + w 3 y 0 + w 4 ( y 0 + w 2 ) ) = ( x 0 − ( w 1 + w 2 ) h 2 y 0 + ( w 2 + w 4 ) w 2 ) = ( ( 1 − h w C ) x 0 + h w C h 2 ( 1 − h w C ) y 0 + h w C w 2 ) \begin{aligned} \mathbf{J}^r &= \begin{pmatrix} w_1 \left(x_0 - \frac{h}{2}\right) + w_2 \left(x_0 - \frac{h}{2}\right) + w_3 x_0 + w_4 x_0\\ w_1 y_0 + w_2 \left(y_0+\frac{w}{2}\right) + w_3 y_0 + w_4 \left(y_0+\frac{w}{2}\right)\\ \end{pmatrix}\\ &= \begin{pmatrix} x_0 - \left(w_1 + w_2\right)\frac{h}{2}\\ y_0 + \left(w_2 + w_4\right)\frac{w}{2}\\ \end{pmatrix}\\ &=\begin{pmatrix} \left(1-\frac{h w}{C}\right) x_0+\frac{h w}{C} \frac{h}{2}\\ \left(1-\frac{h w}{C}\right) y_0+\frac{h w}{C} \frac{w}{2} \end{pmatrix} \end{aligned} Jr=(w1(x0−2h)+w2(x0−2h)+w3x0+w4x0w1y0+w2(y0+2w)+w3y0+w4(y0+2w))=(x0−(w1+w2)2hy0+(w2+w4)2w)=((1−Chw)x0+Chw2h(1−Chw)y0+Chw2w)
可以解出来
J r o = ( x 0 y 0 ) = ( C C − h w x r − h 2 w 2 ( C − h w ) C C − h w y r − h w 2 2 ( C − h w ) ) \mathbf{J}^{r o}=\begin{pmatrix} x_0 \\ y_0 \end{pmatrix}=\begin{pmatrix} \frac{C}{C-h w} x_r-\frac{h^2 w}{2(C-h w)} \\ \frac{C}{C-h w} y_r-\frac{h w^2}{2(C-h w)} \end{pmatrix} Jro=(x0y0)=(C−hwCxr−2(C−hw)h2wC−hwCyr−2(C−hw)hw2)
右下
以 2 ( h − x 0 ) , 2 ( w − y 0 ) 2(h - x_0),2(w-y_0) 2(h−x0),2(w−y0)将整张图划分为4个区域

由于其他地方的值比较接近于0,所以热力图可以近似表示为
H ~ ( p ) ≈ { exp ( β ⋅ H ( p ) ) C , p ∈ Ω 4 1 C , p ∉ Ω 4 \tilde{\mathbf{H}} \left(p\right) \approx \begin{cases} \frac{\exp (\beta \cdot \mathbf{H}(\mathbf{p}))}{C},& p\in \Omega_4\\ \frac{1}{C},& p\not\in \Omega_4 \end{cases} H~(p)≈{Cexp(β⋅H(p)),C1,p∈Ω4p∈Ω4
因此
J r = ∑ p ∈ Ω H ~ ( p ) ⋅ p = ∑ p ∈ Ω 4 H ~ ( p ) ⋅ p + ∑ p ∈ Ω 1 , Ω 2 , Ω 3 H ~ ( p ) ⋅ p = w 4 J 4 + w 1 J 1 + w 2 J 2 + w 3 J 3 \begin{aligned} \mathbf{J}^r & =\sum_{\mathbf{p} \in \Omega} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p} \\ & =\sum_{\mathbf{p} \in \Omega_4} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}+\sum_{\mathbf{p} \in \Omega_1, \Omega_2, \Omega_3} \tilde{\mathbf{H}}(\mathbf{p}) \cdot \mathbf{p}\\ &= w_4 \mathbf{J}_4 + w_1 \mathbf{J}_1 + w_2 \mathbf{J}_2 + w_3 \mathbf{J}_3 \end{aligned} Jr=p∈Ω∑H~(p)⋅p=p∈Ω4∑H~(p)⋅p+p∈Ω1,Ω2,Ω3∑H~(p)⋅p=w4J4+w1J1+w2J2+w3J3
其中每个区域的中心点坐标为
J 1 = ( h − 2 ( h − x 0 ) 2 w − 2 ( w − y 0 ) 2 ) = ( x 0 − h 2 y 0 − w 2 ) J 2 = ( x 0 − h 2 y 0 ) J 3 = ( x 0 y 0 − w 2 ) J 4 = ( x 0 y 0 ) \mathbf{J}_1 = \begin{pmatrix} \frac{h-2(h-x_0)}{2}\\ \frac{w-2(w-y_0)}{2}\\ \end{pmatrix}= \begin{pmatrix} x_0 - \frac{h}{2}\\ y_0 - \frac{w}{2}\\ \end{pmatrix} \\ \mathbf{J}_2 = \begin{pmatrix} x_0 - \frac{h}{2}\\ y_0\\ \end{pmatrix}\\ \mathbf{J}_3 = \begin{pmatrix} x_0\\ y_0-\frac{w}{2}\\ \end{pmatrix}\\ \mathbf{J}_4 = \begin{pmatrix} x_0\\ y_0\\ \end{pmatrix} J1=(2h−2(h−x0)2w−2(w−y0))=(x0−2hy0−2w)J2=(x0−2hy0)J3=(x0y0−2w)J4=(x0y0)
权重
w 1 = ( 2 x 0 − h ) ( 2 y 0 − w ) C w 2 = 2 ( 2 x 0 − h ) ( w − y 0 ) C w 3 = 2 ( h − x 0 ) ( 2 y 0 − w ) C w 4 = 1 − w 1 − w 2 − w 3 w_1 = \frac{\left(2x_0 - h\right)\left(2y_0 - w\right)}{C}\\ w_2 = \frac{2\left(2x_0 - h\right)\left(w - y_0\right)}{C}\\ w_3 = \frac{2\left(h - x_0\right)\left(2y_0 - w\right)}{C}\\ w_4 = 1 - w_1 - w_2 - w_3 w1=C(2x0−h)(2y0−w)w2=C2(2x0−h)(w−y0)w3=C2(h−x0)(2y0−w)w4=1−w1−w2−w3
(计算方法就是区域的像素个数乘 1 C \frac{1}{C} C1
因此
J r = ( w 1 ( x 0 − h 2 ) + w 2 ( x 0 − h 2 ) + w 3 x 0 + w 4 x 0 w 1 ( y 0 − w 2 ) + w 2 y 0 + w 3 ( y 0 − w 2 ) + w 4 y 0 ) = ( x 0 − ( w 1 + w 2 ) h 2 y 0 − ( w 1 + w 3 ) w 2 ) = ( ( 1 − h w C ) x 0 + h w C h 2 ( 1 − h w C ) y 0 + h w C w 2 ) \begin{aligned} \mathbf{J}^r &= \begin{pmatrix} w_1 \left(x_0 - \frac{h}{2}\right) + w_2 \left(x_0 - \frac{h}{2}\right) + w_3 x_0 + w_4 x_0\\ w_1 \left(y_0 - \frac{w}{2}\right) + w_2 y_0 + w_3 \left(y_0 - \frac{w}{2}\right) + w_4 y_0\\ \end{pmatrix}\\ &= \begin{pmatrix} x_0 - \left(w_1 + w_2\right)\frac{h}{2}\\ y_0 - \left(w_1 + w_3\right)\frac{w}{2}\\ \end{pmatrix}\\ &=\begin{pmatrix} \left(1-\frac{h w}{C}\right) x_0+\frac{h w}{C} \frac{h}{2}\\ \left(1-\frac{h w}{C}\right) y_0+\frac{h w}{C} \frac{w}{2} \end{pmatrix} \end{aligned} Jr=(w1(x0−2h)+w2(x0−2h)+w3x0+w4x0w1(y0−2w)+w2y0+w3(y0−2w)+w4y0)=(x0−(w1+w2)2hy0−(w1+w3)2w)=((1−Chw)x0+Chw2h(1−Chw)y0+Chw2w)
可以解出来
J r o = ( x 0 y 0 ) = ( C C − h w x r − h 2 w 2 ( C − h w ) C C − h w y r − h w 2 2 ( C − h w ) ) \mathbf{J}^{r o}=\begin{pmatrix} x_0 \\ y_0 \end{pmatrix}=\begin{pmatrix} \frac{C}{C-h w} x_r-\frac{h^2 w}{2(C-h w)} \\ \frac{C}{C-h w} y_r-\frac{h w^2}{2(C-h w)} \end{pmatrix} Jro=(x0y0)=(C−hwCxr−2(C−hw)h2wC−hwCyr−2(C−hw)hw2)
#!/usr/bin/env python
# _*_ coding:utf-8 _*_
import torch
from heatmap import get_heatmap_coordination_batch
from soft_argmax import spatial_expectation2d, spatial_soft_argmax2d
from torch import tensor
from torch.nn.functional import mse_loss
if __name__ == '__main__':
x = torch.zeros(1, 4, 512, 512, dtype=torch.float).cuda()
batch, channel, height, width = x.shape
x[:, 0, 0, 0] = 1
x[:, 1, 0, width-1] = 1
x[:, 2, height-1, 0] = 1
x[:, 3, height-1, width-1] = 1
beta = tensor(15.0)
bias_coordination = spatial_soft_argmax2d(x, beta, normalized_coordinates=False, remove_bias=False)
remove_bias_coordination = spatial_soft_argmax2d(x, beta, normalized_coordinates=False, remove_bias=True)
remove_bias_coordination = torch.clamp(remove_bias_coordination, min=torch.tensor(0, device=x.device), max=torch.tensor([height, width], device=x.device))
ans = get_heatmap_coordination_batch(x)
print(bias_coordination)
print()
print(remove_bias_coordination)
print()
print(ans)
print()
print(mse_loss(bias_coordination, ans, reduction='sum'))
print()
print(mse_loss(remove_bias_coordination, ans, reduction='sum'))
虽然说,最终确实使得landmark距离真实的landmark比较近,但是在训练的时候loss贼大
然后这个remove bias有可能超出图片范围(比如<0或者>Height)
至于怎么训练,我是没调出来