【论文笔记 · RL】Learning Phase Competition for Traffic Signal Control

Learning Phase Competition for Traffic Signal Control

摘要

FRAP模型基于交通信号控制中相位竞争的思想：当两个交通信号出现竞争时，应该给交通流动更大的相位高优先级。通过相位竞争建模，模型实现了对交通流中翻转、旋转等情况的对称不变性。

介绍

目前的交通信号控制系统SCATS、SCOOT等都基于设计好的交通信号计划。但是其不能适应动态的复杂交通流。

当前，强化学习作为一种可行的解决方案已经被用于现实场景的交通信号控制中。强化学习模型能够直接通过与环境交互学习控制策略。为了实现这个目的，一种典型的方法是为每个交叉路口设置一个Agent，Agent通过做完动作后环境的反馈，来优化奖励。

这些强化学习模型能有效对2或4个信号相位的交叉路口进行控制。但对于8相位的交叉路口，研究发现会出现状态空间爆炸的问题。在2相位问题中，只有4个直行车道，假设状态定义为每个车道上的车辆数和当前信号相位，每个车道的车辆容量为n，则2相控制问题的状态空间大小为$2\times n^4$。而在8相位问题中，有4个直行车道和4个左转车道，状态空间大小会增加到$8\times n^8$。所以其挑战是减少问题空间并更有效地寻找不同场景，故强化学习算法需要在最小范围里找到最优解。

之前的强化学习方法独立输入8车道并利用回归得到$Q(s,a)$，因此其需要尝试在各种状态上尝试8种动作，大约$(8\times n^8)\times 8$个样本才能获得最终估计。

但是实际上不需要这么多样本，如上图中两个场景是镜像的。但是现有的Agent会将上面两个场景表示为不同状态，故其学习了第一种场景，仍然不能处理第二种场景的情况。

而我们更希望在训练过程中，模型能够观察1种场景就能解决经过对称、旋转的其他7种场景。

FRAP

根据这个思想，文章提出了FRAP模型，其能够关注不同交通流动间的关系。这个想法基于交通信号控制种竞争的原理：

• 更大的交通流动预示着对绿灯更大的需求；
• 当两个交通流动发生冲突，将更高需求设为更高优先级。

FRAP首先预测各个信号相位的需求，然后对相位间的竞争进行建模。通过对相位竞争建模，FRAP能够实现对称不变性。利用这种对称不变性并在对称状态间实现知识共享，FRAP可以将搜索空间从$64\times n^8$缩减到$16\times n^4$。本文使用Ape-X DQN作为基础模型，从而来验证FRAP的作用。

论文贡献

• 设计了基于强化学习的交通信号控制模型FRAP，通过对不同信号相位的竞争关系进行建模，FRAP能够实现对称不变性；
• 在对真实世界数据的综合实验中，FRAP较现存强化学习模型收敛更快；
• FRAP能够处理不同道路结构、不同交通流、复杂真实世界的相位设置以及多路口环境。

问题定义

省略

强化学习环境

在该问题中，一个Agent仅观察一个独立交叉路口的交通状况，并且能据此改变交通信号。Agent的目标是学习策略以控制信号，从而来优化行驶时间。交通信号控制问题能够被形式化地表达为马尔可夫决策过程$<\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{R},\gamma >$。

问题1

在给定状态观察集合$\mathcal{S}$和动作集合$\mathcal{A}$的情况下，奖励函数$\mathcal{R}$为$\mathcal{S}\times \mathcal{A}\to \mathbb{R}$，特别是${\mathcal{R}}_s^a=\mathbb{E}[R_{t+1}|S_t=s,A_t=a]$。Agent的目标是学习策略$\pi (A_t=a|S_t=s)$，来最好的采取动作$a$获得状态$s$，从而来获取最大的反馈：
$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots =\sum _{m=0}^{\infty }{\gamma }^m{R}_{t+m+1}$$
Agent的相关定义如下：

• **状态：**交通流动$i$的机动车数量${\mathrm{f}}_i^v$以及当时的交通信号相位${\mathrm{f}}_i^s$。
• **动作：**选择下一时刻的相位。
• **奖励：**交通流动的平均队列长度。

这里文章使用了队列长度来等同于行驶时间，这已经被证明是有效的。

思路

模型概览

文章采用了Ape-X DQN来解决强化学习问题。模型采用交通流动的状态特征作为输入，预测每个动作的分数。这可以用贝尔曼公式形式化描述出来：
$$Q(s_t,a_t)=R(s_t,a_t)+\gamma \max Q(s_{t+1},a_{t+1})$$
FRAP基于两条特别的规则：

• **竞争规则：**更大的交通溜达代表着对绿灯更高的需求，当两种信号出现冲突，应该给更高需求的相位高优先级。
• **不变性规则：**信号控制应该对旋转、对称具有不变性。

算法框架

Ape-X DQN，标准的深度强化学习可以被分为两个部分，包括执行和学习。执行部分包括部署多个具有不同策略的参与者与环境交互，并将观察到的数据存储到经验存储器中。学习部分适用于对经验存储器中的训练数据进行采样，从而来更新模型。两个部分同时运行。

相位不变信号控制设计

文章将相位分数预测分为三个阶段：相位需求建模（Phase demand modeling）、相位对表示（Phase pair representation）、相位对竞争（Phase pair competition）。

相位需求建模

在这个阶段，需要得到每个信号相位的需求表示。我们可以直接从模拟器中化的任意交通流动$i,i\in \{1,\dots ,8\}$的状态，包括机动车数量${\mathrm{f}}_i^v$和当前的信号相位${\mathrm{f}}_i^s$，并将其作为输入，将其传入两层全连接层以生成对绿灯的需求表示${\mathrm{d}}_i$：
$$\begin{gathered} {\mathrm{h}}_i^v=\text{ReLU}({\mathrm{W}}^v{\mathrm{f}}_i^v+{\mathrm{b}}^v),{\mathrm{h}}_i^s=\text{ReLU}({\mathrm{W}}^s{\mathrm{f}}_i^s+{\mathrm{b}}^s) \\ {\mathrm{d}}_i=\text{ReLU}({\mathrm{W}}^h[{\mathrm{h}}_i^v,{\mathrm{h}}_i^s]+{\mathrm{b}}^h) \end{gathered}$$
模型中，可学习的参数在所有交通流动中共享。

最终通过将两个不冲突的交通流动信号进行加和，就可以得到任意相位$\mathrm{p}$的需求表示：
$$\mathrm{d}(\mathrm{p})={\mathrm{d}}_i+{\mathrm{d}}_j,where{\mathrm{p}}_i={\mathrm{p}}_j=1$$

相位对表示

对于每个相位$\mathrm{p}$，文章提出了相位对$\mathrm{p},\mathrm{q},\mathrm{q}\ne \mathrm{p}$。给定相位对$(\mathrm{p},\mathrm{q})$和需求，模型的目标是获得$\mathrm{p}$和$\mathrm{q}$的竞争表示。

通过将相位对的需求表示进行组合，再将所有相位对的向量进行聚合，即可得到相位对需求嵌入体积$\mathrm{D}$，$\mathrm{D}$的大小为$8\times 7\times l_1$，$l_1$是单个相位对需求嵌入向量的长度。

文章采用了$K$层$1\times 1$的卷积层，并将$\mathrm{D}$作为输入，从而获得相位对需求表示。其能被形式化的表示为：
$${\mathrm{H}}_k^d=\text{ReLU}({\mathrm{W}}_k^d\cdot {\mathrm{H}}_{k-1}^r+{\mathrm{b}}_k^d)$$
其中，${\mathrm{H}}_0^d=\mathrm{D}$。这些$1\times 1$的卷积核同样在不同相位对间共享参数。

相位竞争掩码

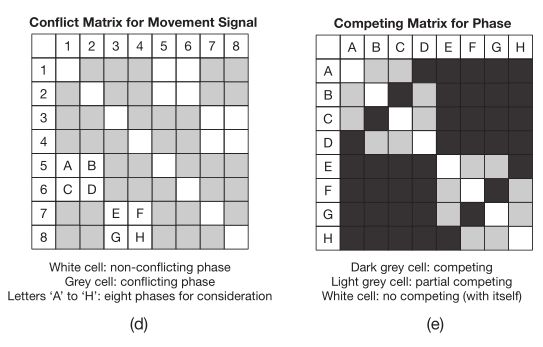
如上图所示，在相位对$(\mathrm{p},\mathrm{q})$中可能存在两种不同的关系：

• 部分竞争：如图e中的相位对A和B，他们共享一个交通流动；
• 完全竞争：如图e中的相位对A和D，他们不共享任何交通流动。

在确定相位对后，模型将搜索竞争矩阵并且将关系投影到嵌入向量$\mathrm{e}(\mathrm{p},\mathrm{q})$上。将所有相位对的嵌入向量聚合可以得到关系嵌入体积$\mathrm{E}$。这里与相位对需求表示建模相同，同样使用$K$层$1\times 1$卷积层：
$${\mathrm{H}}_k^r=\text{ReLU}({\mathrm{W}}_k^r\cdot {\mathrm{H}}_{k-1}^r+{\mathrm{b}}_k^r)$$
其中，${\mathrm{H}}_0^r=\mathrm{E}$。

相位对竞争

这个阶段，模型将相位对需求表示和相位竞争掩码作为输入，并预测每个相位的分数。

相位竞争表示${\mathrm{H}}^c$可以通过相位需求${\mathrm{H}}_K^d$和相位竞争掩码${\mathrm{H}}_K^r$相乘得到：
$${\mathrm{H}}^c={\mathrm{H}}_K^d\otimes {\mathrm{H}}_K^r$$
然后，再通过一层$1\times 1$卷积层可获得竞争结果矩阵$\mathrm{C}$，其中每一行代表相位$\mathrm{p}$与其他竞争对手的相对优先性：
$$\mathrm{C}=\text{ReLU}({\mathrm{W}}^c\cdot {\mathrm{H}}^c+{\mathrm{b}}^c)$$
最终，将每个相位$\mathrm{p}$的相对优先性相加获得相位$\mathrm{p}$的分数。Agent选择最高分作为动作。

讨论

模型设计的不变性

通过建模过程，可以对相位进行对称，这使得FRAP能够利用交通信号控制中的对称特性，缩小搜索空间。

比如，再每条交通流的最大车辆数为$n$，交通信号仅为0或1的情况下，模型能够通过$2^2\times n^2$种可能的两个交通流的特征组合获得相位表示。然后两个相位被配对（一个相位对）来进行竞争，并且在所有相位对间共享相位竞争模型。这样对8个动作的$Q$值进行回归时，就只需要观测$(2^2\times n^2)\times (2^2\times n^2)=16\times n^4$个样本。

对不同环境的适应性

FRAP模型能够适用于各种交通环境（大中小流量）、各种交通信号设置（4相位、8相位）和各种道路结构（三交叉路口、四交叉路口、五交叉路口）。FRAP呢能够从一个环境中学习后，移植到另一个环境中并且获得高分。

多交叉路口环境应用

FRAP在交叉路口中也表现良好。

实验

实验设置

本文使用CityFLow模拟平台，将交通数据作为输入，模拟器能够为模型提供交通情况的观测并执行信号控制动作。与真实世界一致，绿灯以后设置了3s黄灯和2s全红灯。

在交通数据集中，每辆车没描述为$(o,t,d)$，其中$o$是起始位置，$t$是时间，$d$是终点位置。

在多交叉路口网络中，文章使用了真实路网。在单交叉路口中，除非其他特殊规定，路网将设为一个拥有300米路段的四向交叉路口。

数据集

文章使用了济南、杭州和亚特兰大的数据集。

**济南：**文章收集了济南7个十字路口的监控摄像头数据。该数据集中每条记录包含摄像头的位置、车辆到达十字路口的时间以及车辆信息。

**杭州：**该数据集记录了2018年4月1日到2018年4月30日的杭州6个路口的监控摄像头数据，记录完成，数据处理方法于济南数据类似。

**亚特兰大：**该数据集由8台摄像机记录了2006年11月8日亚特兰大Peachtree Street的主干道。该车辆轨迹数据集提供了研究区域内车辆的精确位置，共考虑了五个交叉路口。

比较方法

• **Fixedtime：**固定时间控制采用确定的周期和相位时间计划，其广泛应用于稳定交通流。
• **SOTL：**自组织交通信号控制（SOTL）是一种能够基于等待车辆数量的手动调节阈值的自适应交通信号灯调节方法。
• **Formula：**该方法根据交通状况计算出合理的交通信号周期长度，然后根据交通流量比率来决定每个阶段分配的时间。
• **DRL：**这个方法采用了DQN框架进行信号灯控制，并将描述车辆在道路上位置的图像作为状态图像。
• **IntelliLight：**该DRL方法具有更精细的网络结构，在两相信号控制中表现良好。
• **A2C：**该方法采用了最优的Actor-Critic方法，利用等待时间和车辆数来描述交通状态。

参数设置

• Adam学习率设置为$1e-3$
• 每一轮训练中，从内存中采样1000个样本，以20的batch_size进行训练
• 3个Actor并行以实现Ape-X DQN框架
• 将10s设置为两次动作的间隔（根据实验，该因素不敏感）

评价指标

行驶时间。

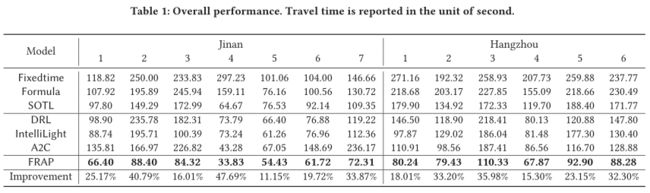
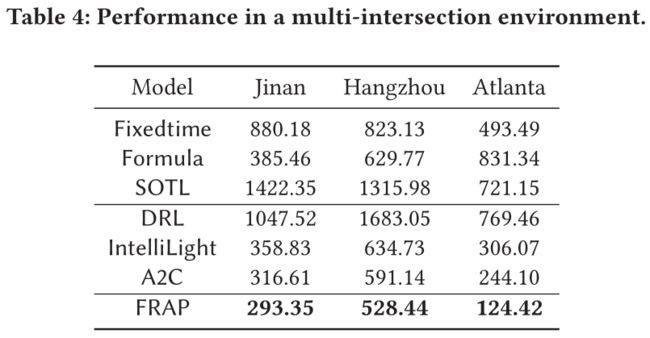
整体性能表现

模型比较

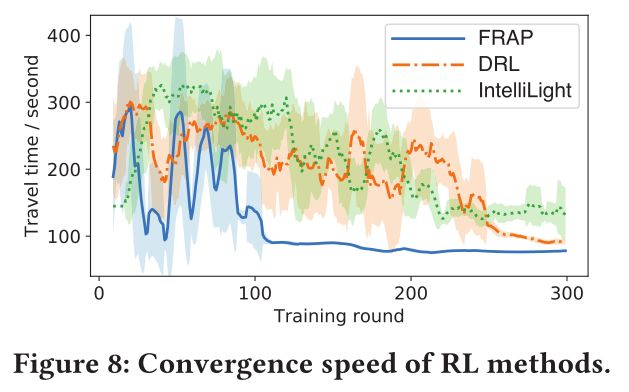
收敛速度

FRAP利用了交通信号控制的对称特性和Ape-X DQN框架提高采样效率。

模型特点

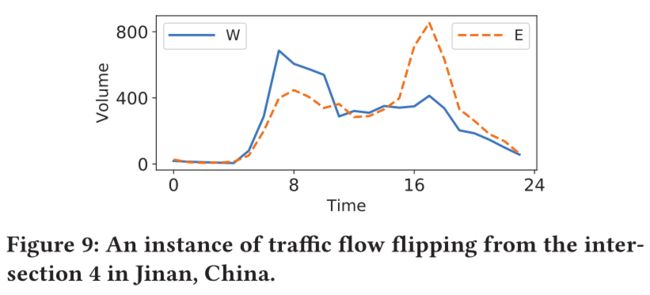
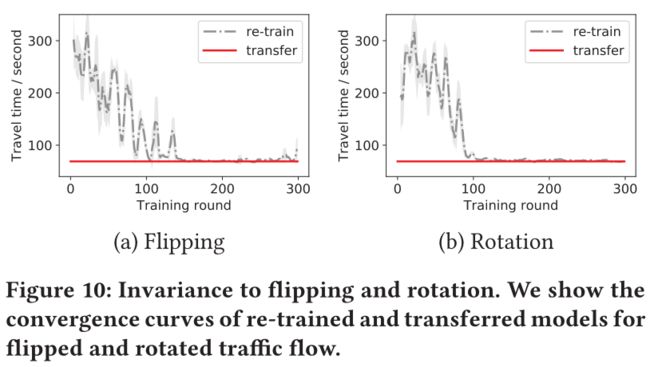
翻转与旋转不变性

真实世界中，存在上下班高峰期，可能存在翻转与旋转。如上图，上午8点左右西线交通大于东线，而下午5点，关系反过来。

由于先前的RL方法没有使用交通信号控制中的对称特性，在流量发生剧烈变化时，需要重新训练模型。而FRAP保证了其不容易收到该极端变化的影响。

上图显示了FRAP对翻转和旋转的不变性。该实验中在原始交通流中训练出一个模型，并在对应翻转和旋转的交通流上进行测试。文章及将该模型与两个重新训练的波形进行比较，可见该模型与重新训练的模型具有几乎相同的性能，节约了训练成本。

对不同交通流量的适应性

从直觉上，如果一个模型在大交通流上搜索了足够状态，其就能够移植到相对较轻的交通流。但是，由于较大的状态空间，现有的RL方法不能看到足够的样本，从而传递到不同的交通流。

FRAP模型设计利用了交通信号控制的对称比例，提高了数据的效率，从而具有更好的可移植性。

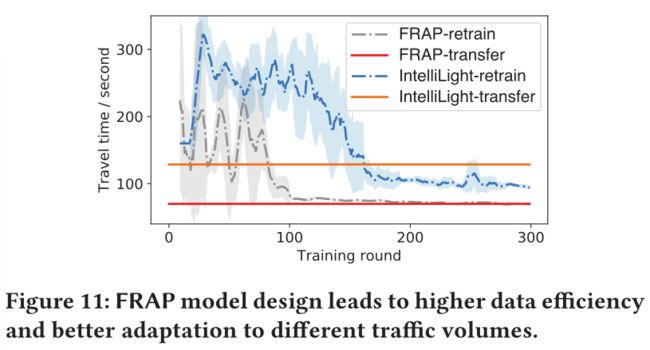
文章选择了FRAP和IntelliLight模型，使用济南数据集最大车流量最大的路口2进行训练，并评估了他们在交通流较小的路口1的性能。

两种模型都搜索了相同的状态空间并且收敛到交叉路口2的最佳值。从图11中，我们可以看到，FRAP的转移模型与重新训练的模型的性能几乎相同，而IntelliLight的重新训练模型与转移模型之间存在明显的差距。这表明所提出的FRAP模型设计显著提高了采样效率，有利于适应不同的交通流。

8相设置的灵活性

在传统交通中，4相设置（A、D、E、H）的交叉路口仍然很常见。

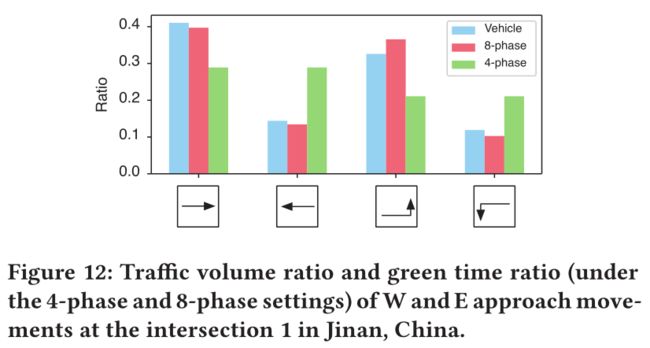
尽管4相设置简单并在某些时候有效，但具有严重的局限性，其在两个相反的方向，直行或左转信号的绿色时间总是相同的。当两个方向的车流量不平衡时，会造成行驶时间的消极影响。而8相设置则可以使来自一个入口的车辆独占通过。

在本实验中，证明了8相设置比4相设置更加灵活，可以更快、更合理地通过。

如上图，在济南1号路口，当东西方向车流量差异较大时，8相设置下学习的策略可以相应调整绿灯时间，而4相设置下学习的策略则会在交通流量较小的路段浪费大量时间。

8相设置花费了66.40s，4相设置用了81.97s。

不同环境下的实验

不同交叉路口结构

该实验中，文章根据济南市交通流的均值和方差，为每个路口结构合成了一个典型的交通流。

对于3向路口，文章禁止了一些神经元来使得其与路口结构兼容，此外，将不存在的交通流动用0填补。对于5向路口，添加了另一个相位并进行了与4向路口同样的处理。

多路口环境

文章选择了济南、杭州和亚特兰大$3\times 4$，$4\times 4$和$1\times 5$的路口网格用于测试。其中济南和杭州的数据选取数据较为丰富的区域，并且做了必要的数据填充。

学习策略解读

对8:00到20:00间的数据进行测试，文章根据具体策略计算分配给每个动作的绿灯时间，并将其归一化，得到绿灯率。同时，还计算了每个交通流动的车流量占比。

如图13所示，FRAP的绿灯时间比与每小时交通流量的百分比同步良好，而其他基线方法如SOTL和DRL将绿灯时间分配给每个动作更加随机和不规则。

在选定时间内，4个左转交通流动的车流量小于4个直行交通流动。因此，一个好的策略应该是为直行车辆分配更多的绿灯时间。