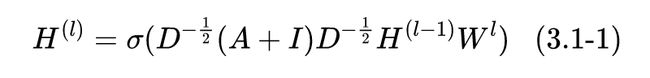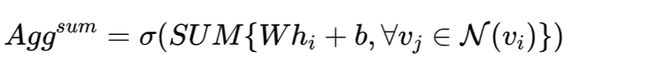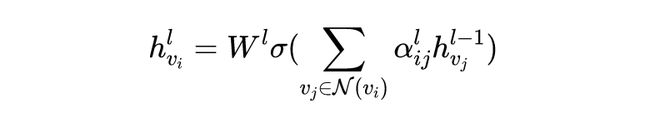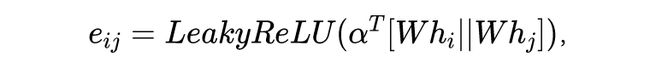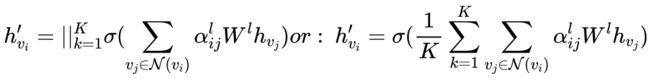图表示学习极简教程
![]()
©PaperWeekly 原创 · 作者|陈凌灏
单位|西安电子科技大学本科生
研究方向|数据挖掘
![]()
Introduction
随着 Deep Learning 的爆火,图数据挖掘和 CV、NLP 等领域一样,存在着“爆发式”发展的趋势。更加准确地说,笔者认为图数据挖掘正处在爆发的前夜。本文主要从基于图结构的表示学习和基于图特征的表示学习两个角度简要介绍图表示学习的现状和自己的认识。
在非图的表示学习中,研究者们主要考虑的是每一个研究对象的特征(姓名、年龄、身高等)信息。然而,研究对象是存在于客观世界的主体,存在一定的图结构信息(QQ、微信好友,师生关系等都构成了图网络)。如何对图结构进行表示学习以表示图的结构信息是一个很重要的 topic。
图表示学习的主要目标是:将结点映射为向量表示的时候尽可能多地保留图的拓扑信息。图表示学习主要分为基于图结构的表示学习和基于图特征的表示学习。
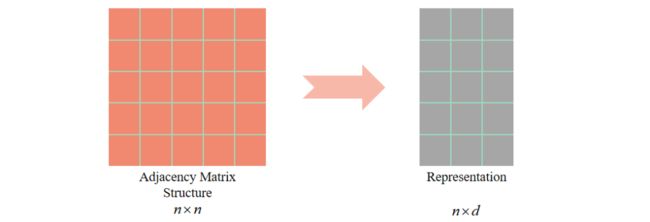
如图1,基于图结构的表示学习对结点的向量表示只来源于图的拓扑结构( x 的邻接矩阵表达的图结构),只是对图结构的单一表示,缺乏对图结点特征消息的表示。
如图2,基于图特征的表示学习对结点的向量表示既包含了图的拓扑信息( x 的邻接矩阵表达的图结构)也包含了已有的特征向量( 个维度为 包含结点特征的向量,如姓名、年龄、身高等信息)。
▲ 图1:基于图结构的表示学习
▲ 图2:基于图特征的表示学习
通过上述的介绍,我们可以知道图表示学习的 task 就是用 个向量表示图上的 个结点,这样我们就可以将一个难以表达的拓扑结构转化为可以丢进炼丹炉的 vector 啦。
![]()
基于图结构的表示学习
在我们的图表示学习中,我们希望 Embedding 出来的向量在图上“接近”时在向量空间也“接近”。对于第 2 个“接近”,就是欧式空间两个向量的距离。对于第一个“接近”,可以有很多的解释:
1-hop:两个相邻的结点就可以定义为临近;
k-hop:两个 阶临近的结点也可以定义为临近;
具有结构性:结构性相对于异质性而言。异质性关注的是结点的邻接关系;结构性将两个结构上相似的结点定义为“临近”。比方说,某两个点是各自小组的中心,这样的两个节点就具有结构性。
因此,针对上述的一些观点,就有了下列的模型:
2.1 DeepWalk
DeepWalk [1] 的方法采用了 Random walk 的思想进行结点采样。
具体参见图 3,我们首先根据用户的行为构建出一个图网络;随后通过 Random walk 随机采样的方式构建出结点序列(例如:一开始在 A 结点,A->B,B 又跳到了它的邻居结点 E,最后到 F,得到"A->B->E->F"序列);对于序列的问题就是 NLP 中的语言模型,因为我们的句子就是单词构成的序列。
接下来我们的问题就变成 Word2vec(词用向量表示)的问题,我们可以采用 Skip-gram [2] 的模型来得到最终的结点向量。可以说这种想法确实是十分精妙,将图结构转化为序列问题确实是非常创新的出发点。
在这里,结点走向其邻居结点的概率是均等的。当然,在有向图和无向图中,游走的方式也不一样。无向图中的游走方式为相连即可走;而有向图中则是只沿着“出边”的方向走。
▲ 图3:DeepWalk(图源:阿里的paper)
2.2 Node2vec
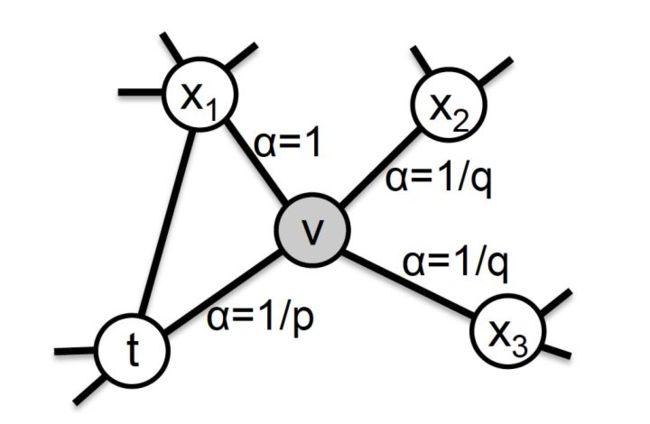
之前所述的 Random Walk 方法中,一个结点向邻居结点游走的概率是相等的。这种等概率的游走操作似乎是比较 naive 的,对此,Node2vec [3] 的提出就是对结点间游走概率的定义。在图 4 中,我们看到当从结点 t 跳跃到结点 v 之后,算法下一步从结点 v 向邻居结点跳跃的概率是不同的。
▲ 图4:Node2vec结点的跳转概率示意
具体的跳转概率(这里的“概率”不是严格的概率,实际上要对下面这个公式进行归一化处理)定义为:
该公式中 后项表示权重, 定义如下:
在上面的公式中,从结点 v 回跳到上一个结点 t 的 为 ;从结点 v 跳到 t、v 的公共邻居结点的 为 1;从结点v跳到其他邻居的 为 。
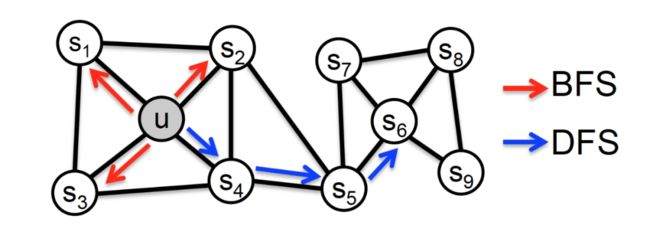
根据上述的方法,我们就可以获得节点间的跳转概率了。我们发现,当 p 比较小的时候,结点间的跳转类似于 BFS,结点间的“接近”就可以理解为结点在邻接关系上“接近”;当 q 比较小的时候,结点间的跳转类似于 DFS,节点间的“接近”就可以视作是结构上相似。具体可借助图 5 理解。
▲ 图5:p、q取值不同时结点的游走趋势
2.3 Metapath2vec, LINE and so on
针对异构图而言,其结点的属性不同,采样的方式也与传统的图网络不同,需要按照定义的 Meta-Path [4] 规则进行采样。采样的样例可类似于“电影-导演-主演”这样的方法进行采样。
对于唐建等人提出的 LINE [5] 中,他们认为 1-hop 和 2-hop 临近的结点为“接近”的结点。关于 Embedding 的技术还有很多,这里就不作详述啦。
![]()
基于图特征的表示学习
在基于图特征的表示学习中,由于加入了结点的特征矩阵 (姓名、年龄、身高等这样的特征),需要同基于图结构的表示学习区别开来。这一类的模型通常被叫做“图神经网络”。在这里,笔者需要安利~~(非利益相关)~~一本非常值得读的书《深入浅出图神经网络》!
3.1 GCN
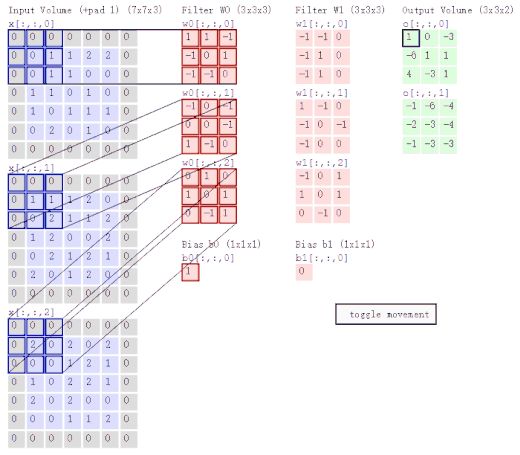
Graph Convolutional Networks [6](图卷积网络)是非常基本第一个 GNN 模型。在讨论 GCN 之前,我们先来看一下 CNN(卷积神经网络)是怎么做卷积运算的。如图 6 所示,CNN 的两个主要特点是局部感知与权值共享。换句话说,就是聚合某个像素点周围的像素特征。
▲图6:卷积神经网络示意
类似地,在 GCN 中,新的特征也是对上一层邻居结点特征的聚合,公式如下:
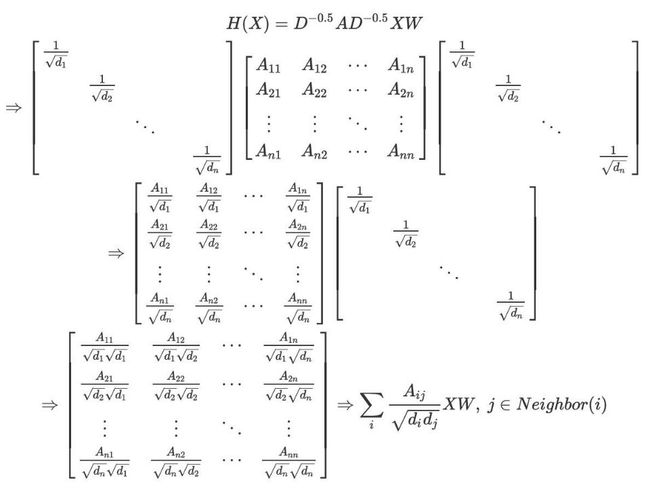
其中 是邻接矩阵, 是顶点的度矩阵(对角阵), 是单位阵,W 是神经网络层与层之间传播的系数矩阵。此外 表示的是该层的结点特征矩阵,第一层的特征矩阵 是原始的结点特征矩阵 。也许有人会有疑问,DNN 的输入应该是一个向量,为什么这里用的是矩阵的表示呢?其实,这里的矩阵可以视作是由多个向量组成的,可以类比于 CNN 中的“多通道”概念。我们来看一下下面的公式推演:
根据上面的推导,我们不难从最后一个公式中看看出结点 在下一层的表示是由其所有的邻居结点 所构成集合 来决的。
因此,我们换一个视角,从每一个结点的角度来看GCN的公式。我们可以发现公式 (3.1-1) 可以表示为:
其中 是第 层网络中结点 的向量表示, 是第层网络上一结点 的向量表示 表示的是结点 的邻居结点构成的集合。公式(3.1-1)、公式(3.1-2)和上面的一堆推导可以说是殊途同归。其核心的意思都表示的是“邻居结点的聚合”。
从直观层面,GCN 的含义就是“聚合”的含义。然而,从图信号角度对 GCN 进行分析,又会是一番新的境界。笔者曾尝试参悟其中的奥妙,结果学了好久发现对我这种没学过信号的菜鸡来说,确实是究极难懂,希望今后悟透了再把这里补上去。
3.2 GraphSAGE
GCN 提出之后,同年的 NIPS 上 GraphSAGE [7] 也横空出世,其主要的特点是固定的采样倍率和不同的聚合方式。
3.2.1 采样倍率
在 GCN 中,我们采用的聚合方式是将一个结点的所有邻居进行聚合。若每一层结点的平局邻居结点个数为 ,那么经过 层的聚合后,结点的聚合代价为 。若 ,那么每个结点就要有 1111 个结点参与计算,要是乘上所有的结点个数,计算的代价简直 credible。
对于邻居节点的聚合,GraphSAGE 在一个 epoch 中,作者并未将某个结点所有的邻居结点进行聚合,而是设置一个定值 ,在第 层选择邻居的时候只从中选最多只选择 个邻居结点进行聚合,计算的复杂度大致在 这个水平。这一改进对 GNN 的落地有着重要意义。
3.2.2 聚合方式
结点聚合应该满足:
对聚合结点的数量自适应:向量的维度不应随邻居结点和总结点个数改变。
聚合操作对聚合结点具有排列不变性:e.g. 。
显然,在优化过程中,模型的计算要是可导的。
根据上述的几点原则,作者提出了几种聚合方式:
池化算子(pooling):
max denotes the element-wise max operator.
LSTM 聚合:
与平均聚合相比,LSTM 聚合具有更大的表达能力。但是,重要的是 LSTM 并不具有排列不变性,因为它们是以顺序方式处理其输入。因此,需要将 LSTM 应用于节点邻居的随机排列,这可以使 LSTM 适应无序集合。
3.3 GAT
自从有了 Attention 机制之后,似乎万物皆可 Attention 了。在图学习中,Graph Attention Network [8] 就是引入了注意力机制的 GNN。说到底,GAT 还是对邻居结点信息的聚合:
其中 是结点 与其相邻结点 之间的权重系数, 的计算公式为:
其中 是 concat 操作,权重参数向量 。这个公式乍一看比较复杂,其实是由两个部分组成。如图 7 (左),首先算出相关度的权重系数
然后在对 进行 softmax 归一化处理,以确保权重之和为 1。其实这里的 Attention 不就是一个加权嘛。
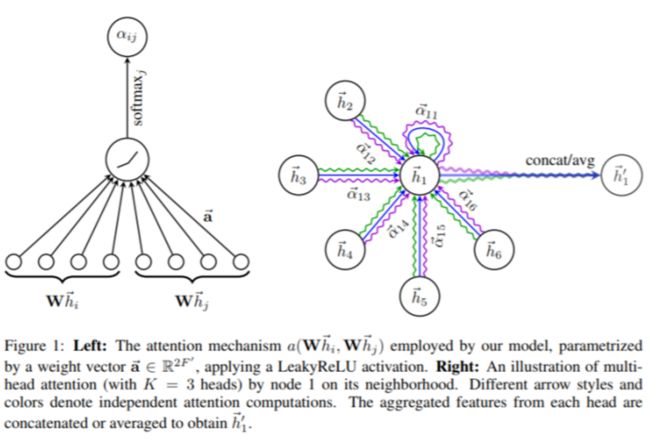
▲ 图7:图注意力机制示意
此外,作者在提出 GAT 时也提出了多头注意力机制的方法。如图 7 (右) 所示,不同的颜色代表了不同的注意力计算过程,并将结果进行拼接或平均。具体公式如下:
由于笔者的 level 问题,对其他网络的了解还不够深入,日后有空再更!![]()
一些有参考意义的博客
Word2Vec (Part 1): NLP With Deep Learning with Tensorflow (Skip-gram) [9]
Word2Vec 介绍:直观理解skip-gram模型(知乎) [10]
node2vec 原理介绍及实践 [11]
[论文笔记] node2vec [12]
深度学习中不得不学的 Graph Embedding 方法 [13]
图卷积网络 GCN Graph Convolutional Network(谱域GCN)的理解和详细推导-持续更新 [14]
GCN作者blog [15]
深度学习中的注意力机制
图深度表示(GNN)的基础和前沿进展视频 [16]
唐杰-图神经网络及认知推理-图神经网络学习班视频 [17]
图网络学习算法——从GraphSAGE,GAT到H-GCN [18]
联系我:xdu.lhchen at gmail.com
参考链接
[1] https://arxiv.org/pdf/1403.6652.pdfhttps://arxiv.org/pdf/1403.6652.pdf
[2] https://arxiv.org/pdf/1301.3781.pdf
[3] https://arxiv.org/pdf/1607.00653.pdf
[4] https://www3.nd.edu/~dial/publications/dong2017metapath2vec.pdf
[5] https://arxiv.org/pdf/1503.03578.pdf
[6] https://arxiv.org/abs/1609.02907
[7] https://papers.nips.cc/paper/6703-inductive-representation-learning-on-large-graphs.pdf
[8] https://arxiv.org/pdf/1710.10903.pdf
[9] http://www.thushv.com/natural_language_processing/word2vec-part-1-nlp-with-deep-learning-with-tensorflow-skip-gram
[10] https://zhuanlan.zhihu.com/p/29305464
[11] https://zhuanlan.zhihu.com/p/39105752
[12] https://zhuanlan.zhihu.com/p/46344860
[13] https://zhuanlan.zhihu.com/p/64200072
[14] https://blog.csdn.net/yyl424525/article/details/100058264
[15] http://tkipf.github.io/graph-convolutional-networks/
[16] https://www.bilibili.com/video/av83519765?from=search&seid=13216707505562731124
[17] https://www.bilibili.com/video/av77934956/?spm_id_from=333.788.videocard.1
[18] https://zhuanlan.zhihu.com/p/74345718
![]()
点击以下标题查看更多往期内容:
深入理解图注意力机制(Graph Attention Network)
WWW 2020 开源论文 | 异构图Transformer
图神经网络三剑客:GCN、GAT与GraphSAGE
图神经网络时代的深度聚类
这 10 篇硬核论文,让你更了解图神经网络
ICLR 2020 | 多关系图神经网络CompGCN
![]()
#投 稿 通 道#
让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
???? 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
???? 投稿邮箱:
• 投稿邮箱:[email protected]
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
????
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
![]()
![]()