3D点云分割系列3：Momen^et:Mo-Net 几何矩作为特征描述符在3D点云分类/分割中的应用

Mo-Net

《Momenet: Flavor the Moments in Learning to Classify Shapes》2019ICCV

1 引言

三维点云可以被看做一个刚体，具有旋转和平移不变性。从物理层面来看，刚体的几何矩是重要的特征参数，几何矩可以作为形状描述符来表征一个物体的表面形状。同时，这种几何矩不会因为点云密度的变化或者是采样点不同而产生变化，是全局的特征。同时，这种几何矩也不会因为点云旋转角度不同、平移方向和距离不同而变化。这种全局的特征对于3D点云的分类是具有重要意义的。

Mo-Net的主要贡献就是通过向坐标中添加多项式函数来让模型考虑到点云的高阶几何矩，从而提高分类精度。

2 Mo-Net方法

2.1 图形的几何矩

基于不变代数理论，几何矩可以作为形状描述符来表征物体形状。不同阶的几何矩可以表征不同的物体特征。对于点云数据结构而言，一阶矩代表物体的质心；二阶矩为惯性矩。其中二阶矩的计算公式可以为：其中x为点集中的点坐标(x, y, z)。

$$\sum =\sum _j{x}_j{x}_j^T$$

图中，红色点为飞机点云的质心，蓝色三条线则为惯性矩。无论点云数据如何旋转、平移，几何矩都不会产生变化（质心位置会变化，但是可以进行转换）。

2.2 多项式拟合

在Mo-Net的结构中，作者添加了多项式函数作为模型的输入。在我们的理解中，深度学习模型能够隐式地学习拟合多项式，但是是否能够拟合多项式函数作为输入从而避免手动添加，这并没有直接证据。在这里，作者设计实验进行比较，公式如下：

$$\underset{\hat{f}(w,x)}{\mathrm{argmin}}\Vert \hat{f}(w,x)-f(x){\Vert }_{L_{\infty }}<ϵ$$

也就是需要模型$\hat{f}(w,x)$来逼近多项式函数$f(x)$。

这里作者设计实验$f(x)=x^2$，使用MLP模型来对函数$f(x)$进行拟合。

结果表面，当模型层数为1层的时候，模型的error约为0.058，模型层数为6层的时候，模型的error约为0.0069。而当层数增加后，error值也未得到明显改善。也就是说使用MLP来拟合多项式作为输入难以直接拟合多项式。因此，手动添加多项式进行输入更为合理。

2.3 模型结构

Mo-Net的模型结构类似于PointNet，不同于PointNet，作者的Spatial-Trans中添加了$2^{nd}Order-Layer$，并在其中添加了多项式函数$(x^2,y^2,z^2,xy,xz,yz)$。同时，还根据点坐标计算了KNN图，输出一个点到其20个邻近点的距离，即($x-x^{{}^{\prime }},y-y^{{}^{\prime }},z-z^{{}^{\prime }}$)，其中$(x,y,z)$和$(x^{{}^{\prime }},y^{{}^{\prime }},z^{{}^{\prime }})$分别为点坐标和邻域点坐标。这些特征通过两个MLP网络进行对齐和处理，随后通过Max-Pool函数输出。

3 实验

3.1不同阶矩输入的影响

实验表明，额外输入3阶矩也不能提高模型的精度，同时使用MLP来拟合高阶矩获得的精度不如手动进行输入。

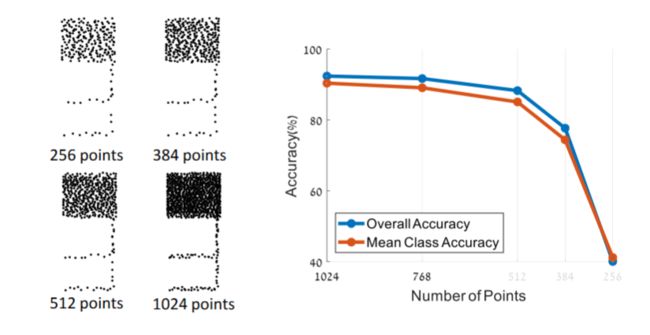
3.2 不同采样密度的影响

模型训练时输入为1024个点，改变预测输入的点的数量，模型精度变化曲线如右图。在512个点时仍然能获得不错的效果。比较可惜的是，作者这里没有比较其他模型在采样点下降时的精度变化。

3.3 分割任务的表现

在分割任务上，Mo-Net也表现出了不错的效果，但几何矩本身是全局特征，对需要局部精细特征的分割任务而言，效果不太明显。

4 总结

在这篇文章中，作者分析了几何矩作为形状标识符对三维点云形状的表征意义。引入了一阶矩、二阶矩作为模型的多项式输入。同时设计实验分析了MLP模型是否能够替代手动多项式输入，实验证明手动输入比使用模型拟合效果更明显。最后，作者基于PointNet，在输入阶段采用$2^{nd}Order-Layer$来输入多项式特征。

本文的核心是几何矩对点云形状的表征意义。