Python3.9标准库math中的函数汇总介绍(53个函数和5个常数)

为了更好的用计算机帮助我们运算，首先要了解自己使用的库中有什么方法，否则就会做会多费力不讨好的重复工作。

本篇博文我们来了解Python标准库的math函数。

参考资料：
Python3.9的math库的官方文档链接：https://docs.python.org/3.9/library/math.html
中文版链接：https://docs.python.org/zh-cn/3.9/library/math.html

另外还参考了下面这个第三方文档：
https://www.runoob.com/python3/python-math.html

math库是Python的标准库，所以它是对Python数学运算部分的扩展，所以它并没有新增加数据对象，比如它并没有像Numpy库那样新增一个ndarray数据对象，math库的运算对象都是Python中的标准数据类型，比如int型、float型、complex型。

Python中的math库实际上对应于C语言的math库，Python官方建议尽量遵循C99标准。C99标准是 ISO/IEC 9899:1999 - Programming languages – C 的简称 ，是C语言的官方标准第二版。

Python math 模块提供了许多对浮点数的数学运算函数。
math 模块下的函数，返回值均为浮点数，除非另有明确说明。
如果你需要计算复数，请使用 cmath 模块中的同名函数。

博主写完这篇博文后根据目录统计了下：
共有24+8+9+2+6+4=52个函数
和5个常数

第一章-math模块中的几个常数

math.e—欧拉数(自然常数e) (2.718281828459045)
math.inf—正无穷大浮点数
math.nan–浮点值 NaN (not a number)
math.pi—圆周率
math.tau—Tau 是一个圆周常数，等于 2π

示例代码如下：

import math

e_value = math.e
inf_value = math.inf
nan_value = math.nan
pi_value = math.pi
tau_value = math.tau

运行结果如下：

第二章-整数运算(数论)和表示性函数(Number-theoretic and representation functions)

2-01-math.ceil(x):将x向正无穷方向舍入到最接近的整数

说明和示例代码：略。

2-02-math.comb(n, k):返回不重复且无顺序地从n项中选择k项的方式总数(组合事件数)

这实际上就是我们在高中概率相关章节中学到的组合事件的可能数。

示例代码如下：

import math

value1 = math.comb(3, 2)
value2 = math.comb(4, 1)

运行结果如下：

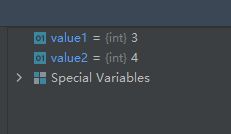
这个函数要与函数math.perm(n,k)相区别。
math.comb(n,k)相当于数学上的组合问题，在数学上的表示为$C_n^k$
math.perm(n,k)相当于数学上的排列问题，在数学上的表示为$A_n^k$

2-03-math.copysign(x, y):返回一个由x的绝对值和y的符号组成的浮点数

math.copysign() 方法语法如下：

math.copysign(x, y)

返回一个浮点值，由第一个参数的绝对值和第二个参数的符号组成。

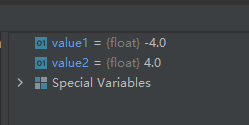
import math

value1 = math.copysign(-4, -2)
value2 = math.copysign(-4, 2)

运行结果如下：

2-04-math.fabs(x):返回 x 的绝对值

说明和示例代码：略。

2-05-math.factorial(x):返回 x 的阶乘

返回 x 的阶乘。 如果 x 不是整数或为负数时则将引发 ValueError。
示例代码：略。

2-06-math.floor():向负无穷方向近似取整

向负无穷方向近似取整，详情见博文 https://blog.csdn.net/wenhao_ir/article/details/125515227 中的第四点

2-07-math.fmod(x, y):返回 x/y 的余数

说明和示例代码略。延伸阅读：C++、C+±OpenCV、Python、Python-Numpy、MATLAB的除法取余方法总结

2-08-math.frexp(x):以 (m, n) 元组的形式返回x的尾数和指数

函数math.frexp(x)的相关数学公式为:
$x=m\ast 2^n$
示例代码如下：

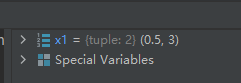
import math

x1 = math.frexp(4)

运行结果如下：

2-09-math.fsum(iterable):返回可迭代对象 (元组, 数组, 列表, 等)中的元素总和

说明和示例代码：略。

2-10-math.gcd():返回若干个整数的最大公约数

示例代码如下：

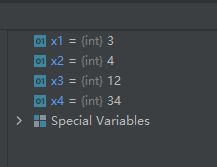
import math

x1 = math.gcd(3, 6)
x2 = math.gcd(4, 12, 36)
x3 = math.gcd(-12, -36)
x4 = math.gcd(0, 34)

2-11-math.isclose(a,b):检查两个值是否彼此接近

检查两个值是否彼此接近，若 a 和 b 的值比较接近则返回 True，否则返回 False。
其语法如下：

math.isclose(a, b, *, rel_tol=1e-09, abs_tol=0.0)

其判断公式如下：
abs(a-b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)
这个公式的意义如下：
如果abs(a-b)小于等于下面两个值
rel_tol * max(abs(a), abs(b))
abs_tol
中的最大值。
则认为a和b足够接近。
从以上判断公式我们可以得到以下认识：
rel_tol — 是相对容差，它是 a 和 b 之间允许的最大差值比例，它的作用对象是 a 或 b 的较大绝对值。例如，要设置5％的容差，请传递 rel_tol=0.05 。默认容差为 1e-09，1e-09这个相对容差意味着两个值在大约9位十进制数字内相同。 rel_tol 必须大于零。
abs_tol – 是最小绝对容差，对于接近零的比较很有用。 abs_tol 必须至少为零。

语法中的第三个参数 * 的作用是过滤多余的数字参数，为什么有这个作用，下面这篇文章看了之后您就清楚了，链接：
https://www.runoob.com/w3cnote/python-one-and-two-star.html，https://www.cnblogs.com/arkenstone/p/5695161.html

示例代码如下：

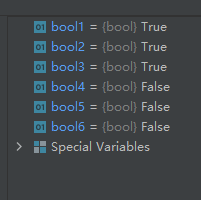
import math

bool1 = math.isclose(8.005, 8.450, abs_tol=0.4)
bool2 = math.isclose(8.005, 8.450, abs_tol=0.5)

bool3 = 0.1+0.2 == 0.3
bool4 = math.isclose(0.1+0.2, 0.3)

运行结果如下：

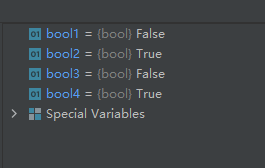
这里大家应该注意为什么bool3的结果为False，而bool4的结果为True。这是由于浮点数精度问题造成的。

2-12-math.isfinite(x):判断x是否为明确的值

如果 x 既不是无穷大也不是 NaN，则返回 True ，否则返回 False 。

示例代码如下：

import math

bool1 = math.isfinite(99)
bool2 = math.isfinite(0)
bool3 = math.isfinite(-99)
bool4 = math.isfinite(math.inf)
bool5 = math.isfinite(-math.inf)
bool6 = math.isfinite(math.nan)

运行结果如下：

2-13-math.isinf(x):判断 x 是否是正无穷大或负无穷大

如果 x 是正或负无穷大，则返回 True ，否则返回 False 。

import math

bool1 = math.isinf(99)
bool2 = math.isinf(0)
bool3 = math.isinf(-99)
bool4 = math.isinf(math.inf)
bool5 = math.isinf(-math.inf)
bool6 = math.isinf(math.nan)

运行结果如下：

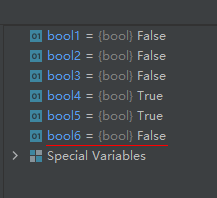
注意：bool6的值为False，而不是True。这个函数只有当参数值为正无穷大或负无穷大时返回值才为True。

2-14-math.isnan():判断值是否为NaN

如果参数的值为 NaN（不是数字），则返回 True ，否则返回 False 。
示例代码如下：

import math

bool1 = math.isnan(99)
bool2 = math.isnan(0)
bool3 = math.isnan(-99)
bool4 = math.isnan(math.inf)
bool5 = math.isnan(-math.inf)
bool6 = math.isnan(math.nan)

运行结果如下：

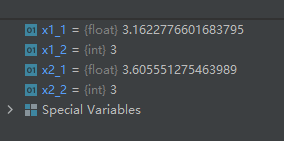
2-15-math.isqrt():将某数的平方根向负无穷方向舍入到最接近的整数

示例代码如下：

import math

x1_1 = math.sqrt(10)
x1_2 = math.isqrt(10)

x2_1 = math.sqrt(13)
x2_2 = math.isqrt(13)

运行结果如下：

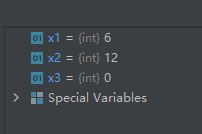
2-16-math.lcm():返回给定的整数参数的最小公倍数

示例代码如下：

import math

x1 = math.lcm(2, 3)
x2 = math.lcm(2, 3, 4)
x3 = math.lcm(2, 3, 4, 0)

运行结果如下：

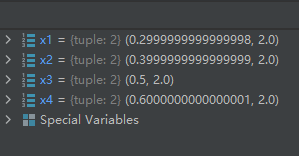
2-17-math.modf():返回浮点数的整数部分和小数部分

示例代码如下：

import math

x1 = math.modf(2.3)
x2 = math.modf(2.4)
x3 = math.modf(2.5)
x4 = math.modf(2.6)

运行结果如下：

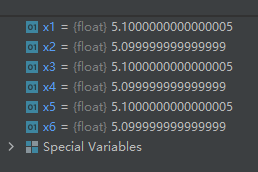
2-18-math.nextafter():返回趋向于y的最接近的浮点数值

import math

x1 = math.nextafter(5.1, math.inf)  # 5.1趋向于正无穷方向的最接近浮点数值
x2 = math.nextafter(5.1, -math.inf)  # 5.1趋向于负无穷方向的最接近浮点数值

x3 = math.nextafter(5.1, 5.2)  # 5.1趋向于5.2的最接近浮点数值
x4 = math.nextafter(5.1, 5.0)  # 5.1趋向于5.0的最接近浮点数值

x5 = math.nextafter(5.1, 7)  # 5.1趋向于7的最接近浮点数值
x6 = math.nextafter(5.1, 4)  # 5.1趋向于4的最接近浮点数值

运行结果如下：

2-19-math.perm(n,k):返回不重复且有顺序地从 n 项中选择 k 项的方式总数

这个函数要与函数math.comb(n,k)相区别。
math.comb(n,k)相当于数学上的组合问题，在数学上的表示为$C_n^k$
math.perm(n,k)相当于数学上的排列问题，在数学上的表示为$A_n^k$

示例代码如下：

import math

value1 = math.perm(4, 2)
value2 = math.perm(5, 3)

运行结果如下：

value1 = 43 = 12
value2 = 54*3 = 60

2-20-math.prod(iterable):计算可迭代对象中所有元素的积

说明和示例代码：略。

2-21-math.remainder(x, y):返回IEEE754风格的x除于y的余数(并不是数学意义上的余数)

什么叫IEEE754风格？实际上是一种浮点数的标准。
对于有限 x 和有限非零 y ， 余数 r 为 x - n*y ，其中 n 是与商 x / y 的精确值最接近的整数。如果 x / y 恰好位于两个连续整数之间，则将最接近的偶数用 n。 余数 r = remainder(x, y) 因此总是满足 abs® <= 0.5 * abs(y)。
示例代码如下：

import math

r1 = math.remainder(13, 4)
r2 = math.remainder(13, 5)
r3 = math.remainder(13, 6)
r4 = math.remainder(13, 7)

运行结果如下：

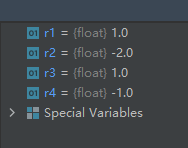
要注意：为什么r2的值为-2？过程如下：
13/5的真除结果为2.6,所以式子r =x - ny中的n为3，所以r=13-35=-2。
所以它不是真正数学意义上的余数。

2-22-math.trunc(x):返回x的整数部分,删除小数部分

示例代码如下：

import math

x1 = math.trunc(2.3)
x2 = math.trunc(2.4)
x3 = math.trunc(2.5)
x4 = math.trunc(2.6)

运行结果如下：

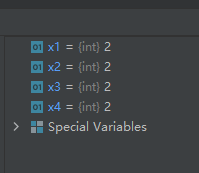
注意与math.modf()的区别，math.modf()是把整数和小数部分分离，即返回值有两个，而math.trunc()只返回整数部分。

2-23-math.ulp(x):返回浮点数x的最小有效比特位的值

如果x等于零，则返回可表示的最小正浮点数。
示例代码如下：

import math

x1 = math.ulp(2.3)
x2 = math.ulp(-2.4)
x3 = math.ulp(2.5876)
x4 = math.ulp(0)

运行结果如下：

2-24–math.ldexp(m, n):返回 m * (2**n) 的值

这里要注意区分函数math.ldexp()与函数math.frexp()的区别和联系。
二者的相关数学公式都为：
$x=m\ast 2^n$
不同的是函数math.frexp(x)的输入参数为x，返回值为元组(m, n)。这个在前面介绍函数数math.frexp()时已经介绍过了。
而函数math.ldexp(m, n)的输入参数为(m, n)，返回值为x。
可见两者是互为反函数的关系。
示例代码如下：

import math

x1 = math.ldexp(9, 3)

运行结果如下：

第三章-幂函数与对数函数

3-01-math.exp(x):返回自然常数e的x次幂

说明和示例代码：略。

3-02-math.expm1():计算自然常数e的x次幂减1的值

math.expm1()用于计算自然常数e的x次幂减1的值，有人有要问，为什么不写成

math.exp(x)-1

呢？
原因是math.expm1(x)的精度比math.exp(x)-1的高。
示例代码：略。

3-03-math.log(x[, base])):返回x以自然数e为底或以base为底的对数

说明和示例代码：略。

3-04-math.log1p(x):返回1+x的以自然数e为底的对数

说明和示例代码：略。

3-05-math.log2(x):返回 x 以 2 为底的对数

说明和示例代码：略。

3-06-math.log10(x):返回x以10为底的对数

说明和示例代码：略。

3-07-math.pow(x, y):返回 x 的 y 次幂

说明： pow(1.0, x) 和 pow(x, 0.0) 总是返回 1.0 ，即使 x 是零或NaN。 如果 x 和 y 都是有限的， x 是负数， y 不是整数那么 pow(x, y) 是未定义的，并且引发 ValueError 。
与内置的 ** 运算符不同， math.pow() 将其参数转换为 float 类型再进行运算。

3-08-math.sqrt(x):返回 x 的平方根

说明和示例代码：略。

第四章-三角函数

4-01-math.acos(x):返回x的反余弦值

math.acos(x):返回x的反余弦值，结果范围在0到pi之间。
这里要说的是为什么结果范围在0到pi之间，而不是0到2pi之间？
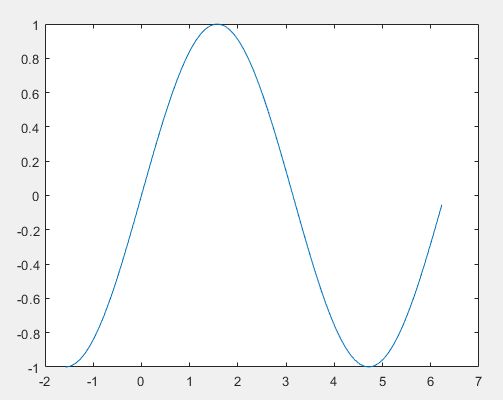
用MATLAB绘制一个0~2pi的余弦函数的图像就知道原因了。

x=0:0.1:2*pi;
y=cos(x);
plot(x,y);

运行结果如下：

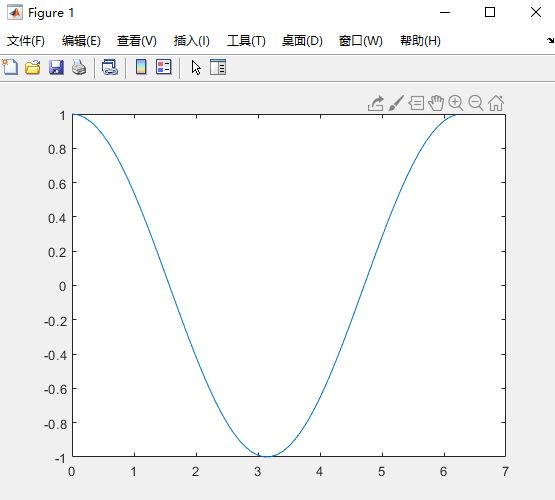
可见，余弦函数横坐标从0到pi其值域范围就为[-1,1]了，所以反余弦的结果为0到pi之间。
示例代码：略。

4-02-math.asin(x):返回x的反正弦值

math.asin(x):返回x的反正弦值，结果范围在 -pi/2 到 pi/2 之间。
这里要注意结果为什么在-pi/2 到 pi/2 之间，因为在这段范围内正弦函数才是单调的。

x=-pi/2:0.1:2*pi;
y=sin(x);
plot(x,y);

示例代码：略。

4-03-math.atan(x):返回x的反正切值

math.atan(x):返回x的反正切值,结果范围在-pi/2到pi/2之间
复习下正切函数的图像吧~

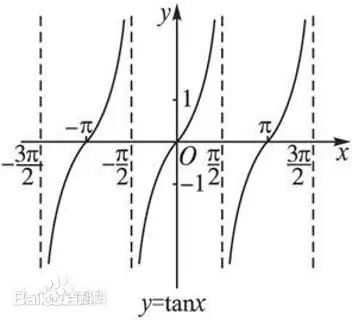
4-04-math.atan2(y, x):返回给定的y及x坐标值的反正切值 atan(y/x)

math.atan2(y, x):返回给定的y及x坐标值的反正切值 atan(y/x)，以弧度为单位，结果是在 -pi 和 pi 之间。
这里要注意：结果是 -pi 和 pi 之间，而不是-pi/2到pi/2之间，为什么呢？
因为既然给的的是坐标，那么点就有可能处于四个象限之间，而四个象限的弧度范围为360度，即2*pi，所以结果为 -pi 到 pi 之间。
示例代码如下(注意：第一个参数为y坐标，第二个参数为x坐标)：

import math

# 点位于第1象限时的情况
value1 = math.atan2(1, 1)
value1 = math.degrees(value1)

# 点位于第2象限时的情况
value2 = math.atan2(1, -1)
value2 = math.degrees(value2)

# 点位于第3象限时的情况
value3 = math.atan2(-1, -1)
value3 = math.degrees(value3)

# 点位于第4象限时的情况
value4 = math.atan2(-1, 1)
value4 = math.degrees(value4)

上面的函数degrees()是把弧度转化为角度
运行结果如下：

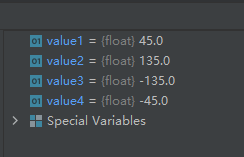
4-05-math.cos():返回x弧度的余弦值

说明和示例代码：略。

4-06-math.dist(p, q):返回p与q两点之间的欧几里得距离(欧氏距离)

math.dist(p, q):返回p与q两点之间的欧几里得距离，以一个坐标序列（或可迭代对象）的形式给出。 两个点必须具有相同的维度。
什么叫欧氏距离？百度百科链接如下：
https://baike.baidu.com/item/%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E5%BA%A6%E9%87%8F/1274107

4-07-math.hypot():返回欧几里得范数(原点到坐标给定点的向量长度(距离))

需要注意的是：3.8 版之前只支持二维点，3.8版之后支持n 维点之间的欧几里得范数计算哈。
示例代码：略。

4-08-math.sin(x):返回x弧度的正弦值

说明和示例代码：略。

4-09-math.tan(x):返回x弧度的正切值

说明和示例代码：略。

第五章-角度转换

5-01-math.degrees(x):将角度x从弧度转换为度数

这个的示例代码见第4-04-math.atan2(y, x)的示例代码。

5-02-math.radians(x):将角度 x 从度数转换为弧度

第六章-双曲函数

6-01-math.acosh(x):返回x的反双曲余弦值

说明和示例代码：略。

6-02-math.asinh(x):返回 x 的反双曲正弦值

说明和示例代码：略。

6-03-math.atanh(x):返回 x 的反双曲正切值

说明和示例代码：略。

6-04-math.cosh(x):返回 x 的双曲余弦值

说明和示例代码：略。

6-05-math.sinh(x):返回 x 的双曲正弦值

说明和示例代码：略。

6-06-math.tanh(x):返回 x 的双曲正切值

说明和示例代码：略。

第七章-特殊函数

7-01-math.erf(x):返回一个数的误差函数值

关于误差函数，参考下面这两个链接：
https://blog.csdn.net/qq_32649321/article/details/122945361
https://www.docin.com/p-1190178420.html
示例代码：略。

7-02-math.erfc(x):返回一个数的互补误差函数值

说明和示例代码：略。

7-03-math.gamma(x):返回x处的伽马函数值

伽马函数的介绍大家可参考百度百科：点此查看百度百科对伽马函数的介绍
示例代码：略。

7-04-math.lgamma(x):返回伽玛函数在x处的值的绝对值的自然对数

说明和示例代码：略。伽玛函数的资料见对上一个函数math.gamma(x)的介绍。