C++数据结构之图的遍历——DFS和BFS（带有gif演示）

1、介绍       

图的遍历指的是从某一个顶点开始，访问图中的其余顶点，使得每个顶点被且仅被访问一次。

本文着重介绍DFS和BFS的区别和过程，因此采用的是最简单的邻接矩阵来储存无向图并实现两种算法。

下面是一个我在b站看到的一个较浅显易懂的图遍历视频，大家可以用作参考： 

1.1DFS（深度优先搜索）和BFS(广度优先遍历）的区别

        我们可以用一个有趣的比喻来区别DFS和BFS，DFS和BFS都是在北极的冒险家，DFS是大胆且无畏的冒险家，而BFS是小心且谨慎的冒险家，当他们被困在由多块碎冰组成的一大块冰面上的时候，DFS优先选择朝着远离当前冰面的方向走去，直到不能走得更远了才回头来继续寻找其他的冰面直到全部冰面都走过一次，而BFS会优先选择先把当前冰面的相邻冰面都走一遍，当相邻的冰面走完了才会向前一步，然后继续走一边下一个冰面的相邻冰面，直到全部的冰面全部都走过一次。在这个比喻之后再读下面的内容我相信更加方便读者理解。

2、DFS（深度优先搜索）

        在对DFS进行了解之前，我们可以先对二叉树的遍历进行回顾，先根遍历为先访问根节点，再访问根节点的左子树，再访问根节点的右子树，而图的遍历算法DFS就是树的先根遍历（也叫先序遍历）的推广。

        由于在图中是极有可能存在回路的，并且图中的任意一个顶点都可能与其他的顶点相通，因此在访问完某一个顶点之后发现没有相邻的未访问的顶点了，这个时候就只能“走回头路”，返回上一个已经访问过的顶点，直到“有路可走”。

2.1算法思路

1）选择一个起点，对其进行访问

2）查询与当前顶点相邻的且未被访问过的顶点,如果存在多个相邻的且未被访问过的顶点，就按照一定的规则从中选择一个进行访问，例如可以按照序号的大小，从小到大进行依次访问。

3）当当前的顶点没有相邻的且未被访问过的顶点时，就访问上一个顶点，并检查该顶点的相邻顶点，找出还没有访问过的顶点，选择其中一个进行访问。若是相邻的顶点全部都被访问过了，就继续访问上一个节点，以此类推。（正是因为这个特点，DFS实际是一个可以利用递归实现的过程）

4）当所有的与起点相邻的顶点都被访问之后，就代表图已经遍历完毕了。

以下是图示：

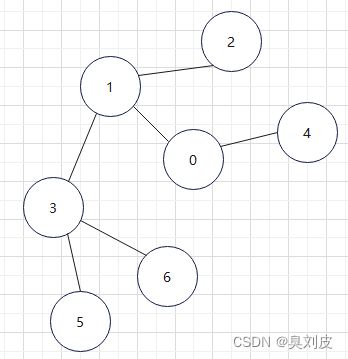
1.首先这是一张无向图，各个顶点之间的连接关系如下所示

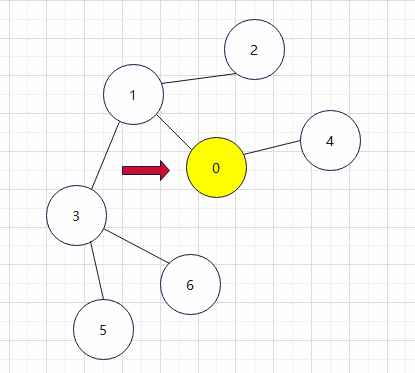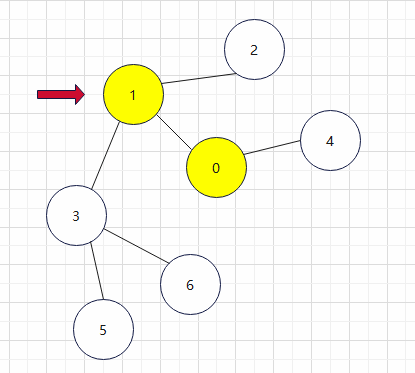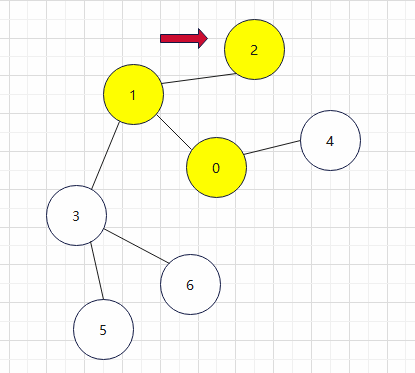
 2.我们选择一个起点进行访问，在这里我选择了0（访问过的点用黄色标出，正在访问的用红色箭头指出）

 3.检查顶点0的相邻节点，发现有1和4且都未被访问，然后我们按照一个先访问顶点序号较小的顶点的规则进行访问

4.在访问完2的时候我们对2进行检查，发现没有相邻的且未被访问过的顶点了，这样我们就返回上一个访问过的顶点1，并且对其相邻顶点进行检查。发现有未被访问过的就去访问，访问完毕之后继续检查，以此类推。最终的访问过程如下所示：

 最终的遍历路径为：0 1 2 3 5 6 4

2.2算法实现（递归版本）

由于在遍历的过程中涉及对顶点是否有被访问过的检查，因此很显然我们需要引入一个访问数组visited[maxsize],其中maxsize为最大顶点数，并且定义其类型为bool数组，这样一来，true就对应着已经被访问过，而false就是未被访问过。

1）由于我们对一个顶点进行访问之后，我们需要检查这个节点的相邻且未被访问过的节点，并且要优先访问序号较小的顶点去访问，我们就需要创建一个函数smallestadjvertex(int v)  (最小序号的邻接顶点)来进行操作,其中参数v为需要进行操作的顶点。

int undigraph::smallestadjvertex(int v)//寻找最小邻接点，参数为顶点下标
{
    for (int i = 0; i < vertexnum; i++)
    {
        if (adjmatrix[v][i]==1)
        {
            return i;//因为i是从小到大递增的，因此第一个符合条件的顶点就是邻接点中序号最小的顶点
        }
        
    }
    return -1;//如果没有找到邻接点就返回-1
}

2）由于该顶点很可能还有其他的邻接顶点，因此我们需要一个函数去寻找下一个邻接顶点,但是我们需要注意，如何确保自己找到的是“下一个”呢，因此我们需要把找到的第一个邻接顶点（也就是序号最小的顶点）的序号作为参数传入该函数中，又因为需要判断邻接关系，因此也需要引入当前顶点的序号，因此就产生了函数nextadjvertex(int v,int prev),其中v为当前顶点，prev为前一个找到的邻接顶点。

int undigraph::nextadjvertex(int v,int prev)
{
    for (int i = prev+1; i < vertexnum; i++)
    {
        if (adjmatrix[v][i]==1)//这里需要注意一下，因为邻接矩阵是对称的，因此只需要判断“一边”就好
        {
            return i;//找到就返回该顶点的下标
        }
        
    }
    return -1;//未找到就返回-1
}

在循环的判断条件中为什么i=prev+1呢，因为要访问下一个邻接顶点，那么我们就需要跳过前一个访问过的邻接顶点，所以需要加一。

3）在实现了两个基础的操作之后我们就可以利用递归，并且引入访问数组visited[]来进行DFS了

void undigraph::DFS(int v)
{
    cout<<"顶点"<=0; prev=nextadjvertex(v,prev))
    {
        if (visited[prev]==false)//如果
        {
            DFS(prev);//递归调用
        }
        
    }  
}

4)最后我们只需要进行进行一个对全图的顶点进行遍历，对未被访问的顶点调用DFS即可

void undigraph::DFStraverse()
{
    for (int i = 0; i < vertexnum; i++)//将访问数组初始化为false(即未被访问过的意思)
    {
        visited[i]=false;
    }
    for (int i = 0; i < vertexnum; i++)//遍历整个图找出未被访问过的顶点并调用DFS
     {
         if (visited[i]==false)
         {
             DFS(i);
         }      
    }   
}

需要注意的是，如果该无向图是连通图的话上面代码块的第二个循环是没必要使用的，只需要选择一个起点对其调用DFS就可以对全图进行访问了，但是如果是非连通图的话我们就需要该循环。具体的连通图和非连通图的概念和区别可以看这个链接：连通图与非连通图的概念与区别

算法实现结果：

将上面动态演示的无向图导入该算法后得到的结果：

 我们可以看到访问的顺序是正确的。

最后我会贴出全部代码，包括DFS和BFS，以及图的创建和main函数

3.BFS(广度优先遍历）

正如他的名字一样，BFS就是以一种“广”的方式去访问。我们再对“递归”这个方法进行思考，一旦算法使用递归，其内部的数据就会以一种“往深处走”的方式进行访问，这显然与BFS的“广”的方式不同，因此下面仅使用非递归方法进行实现。

3.1算法思想

1）选择一个起点，并访问这个顶点

2）查询当前顶点的相邻顶点，并且以一定的规则依次将相邻且未被访问过的顶点全部访问一遍

3）然后从这些相邻顶点中选择一个顶点，查询该顶点的相邻顶点，同样以相同的规则将相邻顶点全部访问一遍

4）全部访问完毕之后就“切换”到下一个顶点，重复上述操作，直到所有的顶点都被访问。

以下是图示：

1.如图是一个无向图以及各个顶点之间的连接关系

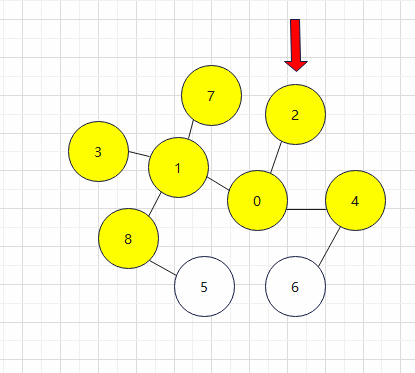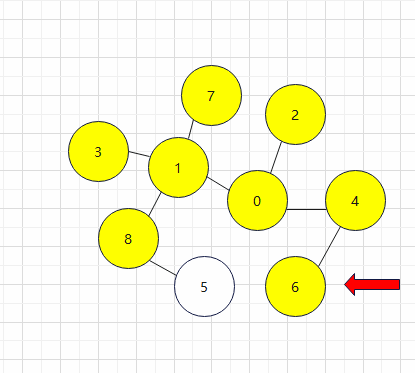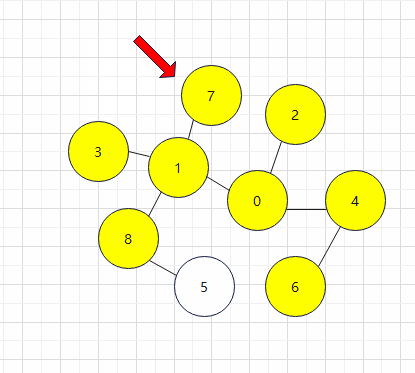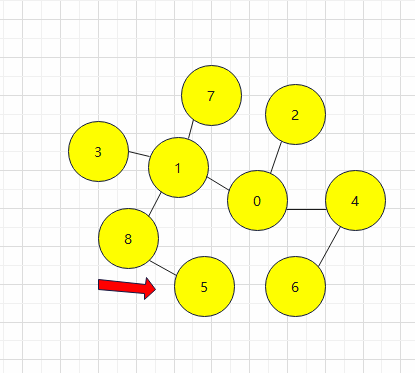
 2.首先先选取一个起点并且对其进行访问，我选择的是0（访问过的点用黄色标出，正在访问的用红色箭头指出）

 3.检查当前顶点的相邻且未被访问过的顶点，我们可以发现1、2、4相邻且未被访问过，根据从小到大序号的访问顺序，我们依次对相邻的顶点进行访问，也就是1->2->4

 4.在对起点0相邻的且未被访问过的顶点（1、2、4）访问完毕之后，我们按照从小到大序号的排序方式，优先检查顶点1的相邻且未被访问过的顶点，并且对其进行升序访问（也就是从小到大访问7、3、8）

 

5.然后返回对顶点2进行检查，发现没有相邻的顶点，那么就对顶点4进行检查，发现有相邻的且未被访问过的顶点6，那么就对其进行访问，以此类推，在访问完顶点6之后，我们就要对顶点1的相邻顶点按照升序进行相邻顶点检查，也就是先检查顶点3再检查顶点7最后检查顶点8，发现顶点8有相邻且未被访问过的定点5，那么就对其访问，至此BFS就结束了

最终的遍历路径为： 0 1 2 4 3 7 8 6 5

3.2算法实现（非递归）

非递归版本的BFS相对于DFS来说比较简单，只需要不断地遍历得到邻接节点并且对其进行访问即可。但是其中需要用到的是队列这个数据结构，队列的作用是什么呢？

队列的作用：

队列的作用就是持续将当前顶点的邻接顶点入队，在对当前顶点的所有邻接顶点都进行访问之后就将其全部出队。

算法步骤：

1）选择一个起点

2）创建一个队列（这里我使用的是标准库中的queue，只需要在头文件导入即可）

3）首先先判断该顶点是否被访问过，如果未被访问过就对其进行访问。

4）将该顶点入队

5）循环判断队列是否为空，不为空队列就弹出，为空就跳出while循环，对下一个顶点进行BFS

6）然后进行邻接顶点的查找，查找到之后对其进行访问并且入队

最后利用一个BFStraverse对全图的顶点进行BFS即可

具体代码：

void undigraph::BFStraverse()
{
    cout<<"进入BFStraverse"< q;
    if (visited[v]==false)
    {
    cout<<"访问"<

算法执行结果：

 可以发现完全符合上面gif动图的演示过程。

3.3BFS算法出现的问题

我们将上图中的3、5两个顶点位置进行互换，再次将该图输入BFS算法之中试试：

                                                                原图                                                                         更改顶点后                                                  

执行结果：

首先我们先对BFS的思想进行具象化的表示：

 按照这种层级的访问思想，我们可以从图中看出3应该是最外层的，也就是应该是最后访问的，但是，从执行结果我们可以发现，竟然顶点3比顶点6先访问，这显然与我们所期待的BFS不同，并不符合那种一层一层遍历的思想，这是因为什么呢？

void undigraph::BFStraverse()
{
    cout<<"进入BFStraverse"<

观察这个代码段我们可以发现第二个循环，也就是循环执行BFS的那个循环，他的顺序是从i小到大依次进行BFS(i)的，也就是说，就算在图的逻辑上应该先访问6再访问3，但是由于你要循环由小到大执行BFS就导致了3会比6优先进入BFS，会产生这个问题主要还是因为我们并没有使用递归进行BFS的调用，而是人为的设置好了从小到大序号进行BFS。

3.4算法改进

        从上面产生的问题我们可以知道，该BFS算法没有按照我们预想的那样按“层级”的顺序去依次访问顶点，因此我们需要对算法进行一个改进。

        我们观察上面的BFS算法代码可以知道，每次产生的队列是基于当前顶点而产生的，也就是每往下一层，产生的队列就非常有可能会增加。

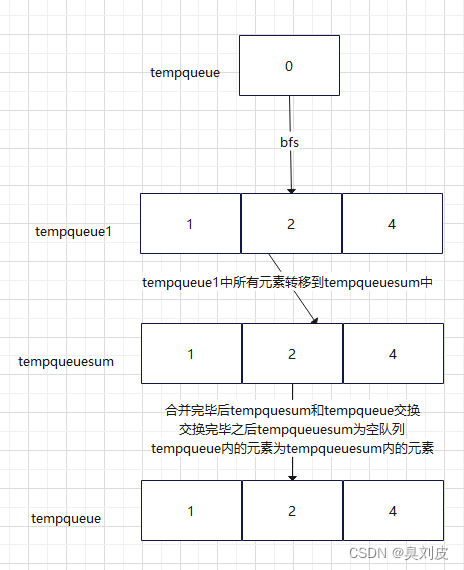
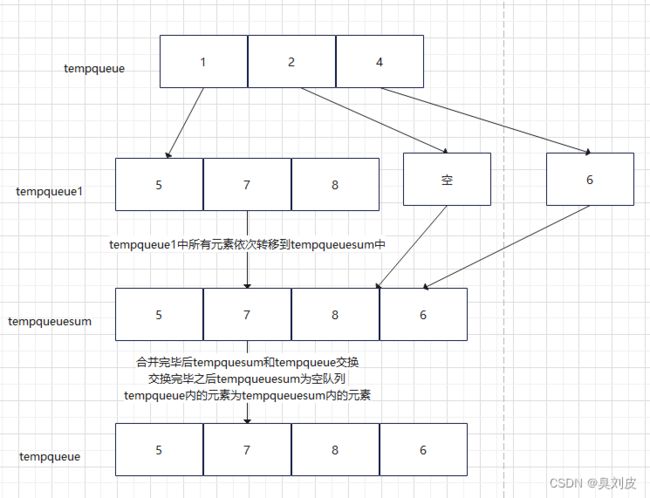
        如下图所示，第一层的0顶点产生了一个队列q0={1，2，4}，然后第二层的顶点1、2、4分别产生了三个队列q1={5,7,8},q2={},q4={0,6}，再往下会产生更多的队列。

         于是我们可以思考，能否将每一层产生的队列全部合并为一个队列呢，这样的话有n层就会产生n个队列，然后对每个队列中的元素依次进行BFS，这样就可以完美解决上面的BFS算法产生的问题。

        为了实现这个算法，我们依然需要用到标准库中的。本算法需要三个函数：

1.bfstraverse()：用于初始化访问数组和确定起点的

2.bfs():用于查找邻接且未被访问过的顶点，产生由这些顶点构成的队列并返回

3.mergequeue():用于合并队列（本算法的关键）

bfstraverse()：

void undigraph::bfstraverse()
{
    for (int i = 0; i < vertexnum; i++)//初始化访问数组
    {
        visited[i]=false;
    }  
    cout<<"请输入起点:"<>start;
    cout<<"访问"<

bfs():

tips:由于之前想着使用指针，后面发现其实没有必要，因此队列名就变成了ptr

queue undigraph::bfs(int v)
{
    queue ptr;//每对一个顶点进行bfs就产生一个队列用于储存邻接顶点
        for (int i = 0; i < vertexnum; i++)
        {
            if (adjmatrix[v][i]==1&&visited[i]!=true)
            {
                cout<<"访问"<

mergequeue():

        在阅读下面的代码前我们可以先思考一个问题，一个由n个顶点组成的图最多有多少层？很显然，n个顶点形成的图，层级最多的时候就是全部拉成一条线的时候，也就是有n层，因此我们只要知道有多少个顶点我们就可以知道要进行最多多少次的相对于层级而言的bfs。

队列合并步骤（图示）：

1.

 2.

 3.

void undigraph::mergequeue(int start)//由起点进入
{
    int temp=start;
    queue tempqueue;//产生一个临时队列
    tempqueue.push(start);//起点入队临时队列
    int tempqueuesize=tempqueue.size();//得到临时队列的大小
    queue tempqueue1;//tempqueue1为一个中转临时队列，下面会用到
    queue tempqueuesum;//合并后的队列
    for (int i = 0; i < vertexnum; i++)
    {       
        for(int i=0;i

3.5执行结果

 可以看到算法成功运行了并成功解决了上一个BFS所产生的问题。

4.全部代码

因为本人为了方便起见，不用每次测试都输入一遍图，就直接把邻接矩阵给初始化了，并且顶点数也初始化为9，如果想要调用createundigraph()来手动创建无向图的话，需要对下面的代码进行改动，也就是把顶点数量vertexnum改为0，然后邻接矩阵只定义而不具体赋值就好了。

#include
#include
#include
#define maxsize 100
using namespace std;

class undigraph
{
    public:
    bool visited[maxsize];//定义一个访问数组
    int vertexnum=9;//无向图的顶点数目
    int maxvertex=0;//用于储存最大顶点的序号
    int data[maxsize];//用于储存每个顶点的数据
    //定义邻接矩阵
    int adjmatrix[maxsize][maxsize]={{0,1,1,0,1,0,0,0,0},
    {1,   0,   0  , 0  , 0  , 1  , 0 ,  1  , 1},
    {1  , 0 ,  0  , 0 ,  0  , 0  , 0  , 0 , 0},
    {0  , 0  , 0  , 0  , 0  , 0  , 0 ,  0 , 1},
    {1 ,  0  , 0  , 0 ,  0  , 0  , 1  , 0  , 0},
    {0  , 1  , 0  , 0 ,  0  , 0   ,0  , 0  , 0},
    {0 ,  0 ,  0 ,  0  , 1  ,0   ,0 ,  0  , 0},
    {0  , 1 ,  0  , 0  , 0  , 0  , 0  , 0  , 0},
    {0 ,  1  , 0 ,  1  , 0  , 0  , 0  , 0  , 0  }};
    void createundigraph();//用于创建无向图
    void printadjmatrix();//打印邻接矩阵
    int smallestadjvertex(int v);
    int nextadjvertex(int v,int prev);
    void DFStraverse();//深度优先遍历
    void DFS(int v);
    void BFStraverse();//广度优先遍历
    void bfstraverse();
    void BFS(int v);
    queue bfs(int v);
    void mergequeue(int tempqueuesize);
};


void undigraph::createundigraph()
{   
    int tempdata;
    int adjvertex;
    int i=0;
    for(;;i++)
    {
        cout<<"请输入顶点"<>tempdata;
        if (tempdata==-1)
        {
            break;
        }
        
        data[i]=tempdata;
        while (true)
        {
        cout<<"请输入顶点"<>adjvertex;
        if (adjvertex==-1)
        {
            break;
        }
        
        
        if (adjvertex>=maxvertex)
        {
            maxvertex=adjvertex+1;
        }
        
        adjmatrix[i][adjvertex]=1;
        adjmatrix[adjvertex][i]=1;
        }
        
        
    }
    vertexnum=i;
    if (i>=maxvertex)
    {
        maxvertex=i;
    }
    
    cout<<"共有"<=0; prev=nextadjvertex(v,prev))
    {
        if (visited[prev]==false)
        {
            DFS(prev);
        }
        
    }  
}

void undigraph::BFStraverse()
{
    cout<<"进入BFStraverse"< q;
    if (visited[v]==false)
    {
    cout<<"访问"<>start;
    cout<<"访问"< tempqueue;
    tempqueue.push(start);
    int tempqueuesize=tempqueue.size(); 
    queue tempqueue1;
    queue tempqueuesum;
    for (int i = 0; i < vertexnum; i++)
    {       
        for(int i=0;i undigraph::bfs(int v)
{
    //cout< ptr;
        for (int i = 0; i < vertexnum; i++)
        {
            if (adjmatrix[v][i]==1&&visited[i]!=true)
            {
                cout<<"访问"<

喜欢本文的话可以点点赞！