2022年第十三届蓝桥杯省赛C++B组

X 进制减法

原题链接

题目描述

进制规定了数字在数位上逢几进一。

$X$ 进制是一种很神奇的进制，因为其每一数位的进制并不固定！

例如说某种 $X$ 进制数，最低数位为二进制，第二数位为十进制，第三数位为八进制，则 $X$ 进制数 $321$ 转换为十进制数为 $65$。

现在有两个 $X$ 进制表示的整数 $A$ 和 $B$，但是其具体每一数位的进制还不确定，只知道 $A$ 和 $B$ 是同一进制规则，且每一数位最高为 $N$ 进制，最低为二进制。

请你算出 $A-B$ 的结果最小可能是多少。

请注意，你需要保证 $A$ 和 $B$ 在 $X$ 进制下都是合法的，即每一数位上的数字要小于其进制。

输入格式

第一行一个正整数 $N$，含义如题面所述。

第二行一个正整数 $Ma$，表示 $X$ 进制数 $A$ 的位数。

第三行 $M_a$ 个用空格分开的整数，表示 $X$ 进制数 $A$ 按从高位到低位顺序各个数位上的数字在十进制下的表示。

第四行一个正整数 $M_b$，表示 $X$ 进制数 $B$ 的位数。

第五行 $M_b$ 个用空格分开的整数，表示 $X$ 进制数 $B$ 按从高位到低位顺序各个数位上的数字在十进制下的表示。

请注意，输入中的所有数字都是十进制的。

输出格式

输出一行一个整数，表示 $X$ 进制数 $A-B$ 的结果的最小可能值转换为十进制后再模 $1000000007$ 的结果。

数据范围

对于 $30\%$ 的数据，$N\le 10;M_a,M_b\le 8$，
对于 $100\%$ 的数据，$2\le N\le 1000;1\le M_a,M_b\le 100000;A\ge B$。

输入样例：

11
3
10 4 0
3
1 2 0

输出样例：

94

样例解释

当进制为：最低位 $2$ 进制，第二数位 $5$ 进制，第三数位 $11$ 进制时，减法得到的差最小。

此时 $A$ 在十进制下是 $108$，$B$ 在十进制下是 $14$，差值是 $94$。

---

算法： 贪心

由题可知： 对于 $X$ 进制数 $321$，进制分别为 $8102$，转化为十进制数为 $65$。
算式：$3\cdot 10\cdot 2+2\cdot 2+1=65$

假设，$A$ 和 $B$ 都是 $n$ 位数，分别是 $a_n{a}_{n-1}\cdot \cdot \cdot a_1$ 和 $b_n{b}_{n-1}\cdot \cdot \cdot b_1$，对应的进制数 $X$ 分别是 $p_n{p}_{n-1}\cdot \cdot \cdot p_1$

由此可知：
$A$ 的十进制应为：$a_n\cdot (p_{n-1}\cdot \cdot \cdot p_1)+a_{n-1}\cdot (p_{n-2}\cdot \cdot \cdot p_1)+\cdot \cdot \cdot +a_1$，
$B$ 的十进制应为：$b_n\cdot (p_{n-1}\cdot \cdot \cdot p_1)+b_{n-1}\cdot (p_{n-2}\cdot \cdot \cdot p_1)+\cdot \cdot \cdot +b_1$，

所以，$A-B=(a_n-b_n)\cdot (p_{n-1}\cdot \cdot \cdot p_1)+(a_{n-1}-b_{n-1})\cdot (p_{n-2}\cdot \cdot \cdot p_1)+\cdot \cdot \cdot +(a_1-b_1)$

判断当 $a_n\ge b_n$ 时， 对应的进制数 $x_n$ 都尽可能的取小（最小为 $2$ ），就可以得出 $A-B$ 的最小值。

不过如果 $a_n＜b_n$ 时， $x_n$是否依然是尽可能取小呢，答案是肯定的。

如果 $a_n＜b_n$， 我们让 $x_{n-1}$ 变大来使得最终值变小，假设在原 $x_{n-1}$ 的基础上增加 $x$ 那么在此位的值将减小 $(b_n-a_n)\cdot (x\cdot x_{n-2}\cdot \cdot \cdot x_1)$，

注意到，题目在最后数据范围中给出 $A\ge B$ 条件，说明如果存在 $a_n<b_n$ 的情况，那么在更高位一定存在 $a_m>b_m$，相应的， 因为比 $n$ 更高位的每个数都要乘上这个$x_{n-1}$, 所以， 想要使更高位的增值最小的情况是 $m=n+1$，增值为 $(a_{n+1}-b_{n+1})\cdot (x_n\cdot x\cdot x_{n-2}\cdot \cdot \cdot x_1)$

将两次变化值相加得：$[(a_{n+1}-b_{n+1})\cdot x_n-(b_n-a_n)]\cdot (x\cdot x_{n-2}\cdot \cdot \cdot x_1)$

显然，$(x\cdot x_{n-2}\cdot \cdot \cdot x_1)＞0$，只需要判断 $(a_{n+1}-b_{n+1})\cdot x_n-(b_n-a_n)$ 的正负。

因为，$a_{n+1}＞b_{n+1}$ 并且都为正整数，所以，$(a_{n+1}-b_{n+1})\ge 1$

又因为， $n$ 进制一定大于 $n$ 进制每一位的数，所以，$x_n>b_n>b_n-a_n$

所以，$(a_{n+1}-b_{n+1})\cdot x_n-(b_n-a_n)＞0$

由此可知，最终值一定变大，故当$a_n＜b_n$ 时，$x_n$依然是要尽可能取小

C++ 代码

#include 
using namespace std;
typedef long long ll;
#define mod 1000000007
#define N 100010

int n, ma, mb;
int a[N], b[N];
ll ans = 0, xn = 1;

int main() {
	cin >> n >> ma;
	for (int i = 1; i <= ma; i++) cin >> a[i];
	cin >> mb;
	for (int i = 1; i <= mb; i++) cin >> b[i];
	int i = ma, j = mb;
	while (i > 0) {
		ans += (a[i] - b[j]) * xn;
		ans %= mod;
		ll x = max(a[i], b[j]) + 1;
		xn *= max(x, 2ll);
		xn %= mod;
		i--;
		if (j) j--;
	}
	cout << ans;
	return 0;
}

---

---

统计子矩阵

原题链接

题目描述

给定一个 $N\times M$ 的矩阵 $A$，请你统计有多少个子矩阵 (最小 $1\times 1$，最大 $N\times M$) 满足子矩阵中所有数的和不超过给定的整数 $K$?

输入格式

第一行包含三个整数 $N,M$ 和 $K$。

之后 $N$ 行每行包含 $M$ 个整数，代表矩阵 $A$。

输出格式

一个整数代表答案。

数据范围

对于 $30\%$ 的数据，$N,M\le 20$，
对于 $70\%$ 的数据，$N,M\le 100$，
对于 $100\%$ 的数据，$1\le N,M\le 500;0\le A_{ij}\le 1000;1\le K\le 2.5\times 108$。

输入样例：

3 4 10
1 2 3 4
5 6 7 8
9 10 11 12

输出样例：

19

样例解释

满足条件的子矩阵一共有 $19$，包含：

• 大小为 $1\times 1$ 的有 $10$ 个。
• 大小为 $1\times 2$ 的有 $3$ 个。
• 大小为 $1\times 3$ 的有 $2$ 个。
• 大小为 $1\times 4$ 的有 $1$ 个。
• 大小为 $2\times 1$ 的有 $3$ 个。

---

算法1： 前缀和 + 暴力枚举

时间复杂度 $O(n^4)$

使用前缀和进行暴力枚举，枚举每个点为起点，和枚举每个点为终点。时间复杂度是 $O(n^4)$。
对于 $70\%$ 的数据，$N,M\le 100$，大概为 $10^8$，可以通过；
对于 $100\%$ 的数据，$1\le N,M\le 500$，大概为 $10^{10}$，部分会超时；
暴力大概可以获得 $70$% 的分数。

C++ 代码

#include 
using namespace std;

long long a[502][502];

int main()
{
	int n, m, k;
	cin >> n >> m >> k;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			cin >> a[i][j];
			a[i][j] += a[i-1][j];
		}
	}
	long long ans = 0;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			long long s = a[i][j], row = i, col = j, temp = a[i-1][j];
			while (s - temp <= k && row <= n)
			{
				while (s - temp <= k && col <= m)
				{
					ans++;
					col++;
					s += a[row][col];
					temp += a[i-1][col];
				}
				col = j;
				row++;
				temp = a[i-1][j];
				s = a[row][j];
			}
		}
	}
	cout << ans;
	return 0;
}

---

算法2： 前缀和 + 双指针滑动窗口

时间复杂度 $O(n^3)$

从枚举每个点转换为枚举每一列，以每一列为起点和终点，使用双指针滑动窗口思维;
用 $left$ 表示左边界，从 $1$ 开始，$right$ 表示右边界，也从 $1$ 开始，子矩阵和为 $s$;
当 $s\le k$ 时，子矩阵的个数为 $right-left+1$ 个矩阵；
当 $s＞k$ 时， $left$ 就向右移动，一直移动到满足 $s\le k$ 的位置，当 $left$ 走到 $m$ 点时循环结束。
对于 $100\%$ 的数据，$1\le N,M\le 500$，大概为 $10^8$，可以全部通过。

C++ 代码

#include 
using namespace std;

long long a[502][502];

int main()
{
	int n, m, k;
	cin >> n >> m >> k;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			cin >> a[i][j];
			a[i][j] += a[i-1][j];
		}
	}
	long long ans = 0;
	for (int i = 1; i <= n; i++)
	{
		for (int j = i; j <= n; j++)
		{
			long long left = 1, right = 1, s = 0;
			while (right <= m)
			{
				s += a[j][right] - a[i-1][right];
				while (s > k)
				{
					s -= a[j][left] - a[i-1][left];
					left++;
				}
				ans += right++ - left + 1;
			}
		}
	}
	cout << ans;
	return 0;
}

---

---

积木画

原题链接

题目描述

小明最近迷上了积木画，有这么两种类型的积木，分别为 $I$ 型（大小为 $2$ 个单位面积）和 $L$ 型（大小为 $3$ 个单位面积）：

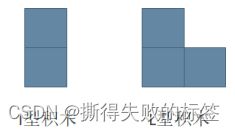
同时，小明有一块面积大小为 $2\times N$ 的画布，画布由 $2\times N$ 个 $1\times 1$ 区域构成。

小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式？

积木可以任意旋转，且画布的方向固定。

输入格式

输入一个整数 $N$，表示画布大小。

输出格式

输出一个整数表示答案。

由于答案可能很大，所以输出其对 $1000000007$ 取模后的值。

数据范围

$1\le N\le 10^7$。

输入样例：

3

输出样例：

5

样例解释

五种情况如下图所示，颜色只是为了标识不同的积木：

---

算法： 动态规划

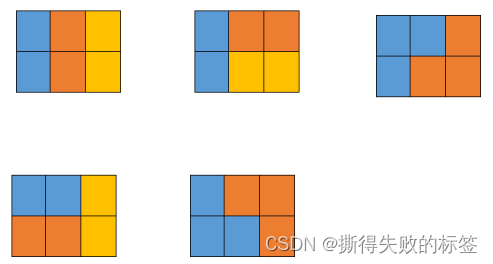
要摆出 $n$ 列方格，可以在 $n-1$ ~ $n$ 列方格后加一个竖着的 $I$ 型积木，也可以在 $n-2$ ~ $n$ 列方格后加两个横着的 $I$ 型积木，也可以在 $n-3$ ~ $n$ 列方格上后加两个 $L$ 型积木的两种摆法, 也可以在 $n-4$ ~ $n$ 列方格上两边加两个 $L$ 型积木中间加一个横着的 $I$ 型的两种摆法，也可以在 $n-5$ ~ $n$ 列方格上两边加两个 $L$ 型积木中间加两个个横着的 $I$ 型的两种摆法，如图：

---

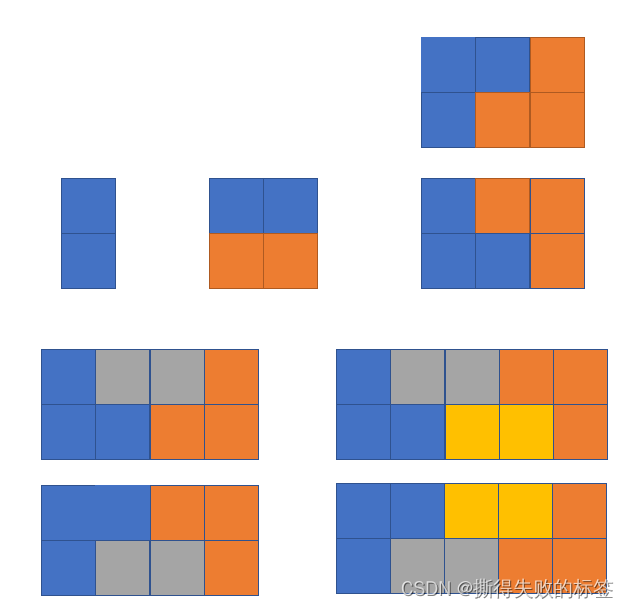
以此类推，可得 $1$ ~ $n$ 列方格的摆法 $dp[n]$ 的方程为：

$dp[n]=dp[n-1]+dp[n-2]+dp[n-3]\cdot 2+dp[n-4]\cdot 2+dp[n-5]\cdot 2+\cdot \cdot \cdot +dp[1]\cdot 2$
$dp[n-1]=dp[n-2]+dp[n-3]+dp[n-4]\cdot 2+dp[n-4]\cdot 2+dp[n-5]\cdot 2+\cdot \cdot \cdot +dp[1]\cdot 2$

两式相减得：$dp[n]=dp[n-1]\cdot 2+dp[n-3]$

C++ 代码

#include 
using namespace std;
typedef long long ll;
#define N 10000010
#define mod 1000000007

int main()
{
	ll *a, n;
	a = new ll[N];
	cin >> n;
	a[1] = 1;
	a[2] = 2;
	a[3] = 5;
	for (int i = 4; i <= n; i++)
		a[i] = (a[i-1]*2 + a[i-3])%mod;
	cout << a[n];
	return 0;
}

---

---

李白打酒加强版

原题链接

题目描述

话说大诗人李白，一生好饮。

幸好他从不开车。

一天，他提着酒壶，从家里出来，酒壶中有酒 2 斗。

他边走边唱：

无事街上走，提壶去打酒。

逢店加一倍，遇花喝一斗。

这一路上，他一共遇到店 $N$ 次，遇到花 $M$ 次。

已知最后一次遇到的是花，他正好把酒喝光了。

请你计算李白这一路遇到店和花的顺序，有多少种不同的可能？

注意：壶里没酒 ($0$ 斗) 时遇店是合法的，加倍后还是没酒；但是没酒时遇花是不合法的。

输入格式

第一行包含两个整数 $N$ 和 $M$。

输出格式

输出一个整数表示答案。由于答案可能很大，输出模 $1000000007$ 的结果。

数据范围

对于 $40\%$ 的评测用例：$1\le N,M\le 10$。
对于 $100\%$ 的评测用例：$1\le N,M\le 100$。

输入样例：

5 10

输出样例：

14

样例解释

如果我们用 $0$ 代表遇到花，$1$ 代表遇到店，$14$ 种顺序如下：

010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100

---

算法1： DFS（深度优先搜索）

时间复杂度： $O(2^n)$

本题最易想到的就是深搜，枚举所有，用几种规则进行剪枝，排除所有不合法的情况。

用 $k$ 表示酒的量；

已知：最后一次遇到的必须是花，并且没酒时遇花是不合法的；

当 $n=0$ 时，只有 $k=m$的时候有解，否则无解；

当 $k=0$ 时，只有 $m=n=0$ 的时候有解，否则无解；

当 $k\ne 0$ 且 $n\ge m$ ，或者 $k＞m$ 时，无解；

单纯的深搜时间复杂度为 $O(2^n)$，当 $n\ge 30$ 时就容易超时，只能拿部分分。

C++ 代码

#include 
using namespace std;
typedef long long ll;
#define mod 1000000007

ll dfs(int n, int m, int k) {
	if (n == 0) return (k == m);
	if (k == 0) return (n == 0 && m == 0);
	if (n >= m || k > m) return 0;
	ll ans = dfs(n, m-1, k-1) + dfs(n-1, m, k*2);
	return ans % mod;
}

int main() {
	ll ans;
	int n, m;
	cin >> n >> m;
	ans = dfs(n, m, 2);
	cout << ans;
	return 0;
}

---

算法2： 记忆化搜索

时间复杂度： $O(n^2)$

使用 $dp[n][m][k]$ 表示遇到 $n$ 次店，$m$ 次花，剩下 $k$ 斗酒，记录此时可能种数；
因为 $n，m\le 100$，所以当 $k>100$ 时，不合法，故给 $dp$ 空间为 $107\cdot 107\cdot 107$。

C++ 代码

#include 
using namespace std;
typedef long long ll;
#define mod 1000000007
#define N 107

ll dp[N][N][N];

ll dfs(int n, int m, int k) {
	if (n == 0) return (k == m);
	if (k == 0) return (n == 0 && m == 0);
	if (n >= m || k > m) return 0;
	if (dp[n][m][k]) return dp[n][m][k];
	ll ans = dfs(n, m-1, k-1) + dfs(n-1, m, k*2);
	dp[n][m][k] = ans;
	return ans % mod;
}

int main() {
	ll ans;
	int n, m;
	cin >> n >> m;
	ans = dfs(n, m, 2);
	cout << ans;
	return 0;
}

---

---

砍竹子

原题链接

题目描述

这天，小明在砍竹子，他面前有 $n$ 棵竹子排成一排，一开始第 $i$ 棵竹子的高度为 $h_i$。

他觉得一棵一棵砍太慢了，决定使用魔法来砍竹子。

魔法可以对连续的一段相同高度的竹子使用，假设这一段竹子的高度为 $H$，那么使用一次魔法可以把这一段竹子的高度都变为 $\lfloor \sqrt{\lfloor \frac{H}{2}\rfloor +1}\rfloor$，其中 $\lfloor x\rfloor$ 表示对 $x$ 向下取整。

小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为 $1$。

输入格式

第一行为一个正整数 $n$，表示竹子的棵数。

第二行共 $n$ 个空格分开的正整数 $h_i$，表示每棵竹子的高度。

输出格式

一个整数表示答案。

数据范围

对于 $20\%$ 的数据，保证 $1\le n\le 1000,1\le h_i\le 10^6$。
对于 $100\%$ 的数据，保证 $1\le n\le 2\times 10^5,1\le h_i\le 10^{18}$。

输入样例：

6
2 1 4 2 6 7

输出样例：

5

样例解释

其中一种方案：

  2 1 4 2 6 7
→ 2 1 4 2 6 2
→ 2 1 4 2 2 2
→ 2 1 1 2 2 2
→ 1 1 1 2 2 2
→ 1 1 1 1 1 1

共需要 $5$ 步完成。

---

算法

从第 $1$ 颗竹子一直砍到第 $n$ 颗，并记录每颗竹子被砍过程中所出现的所有情况，直到高度为 $1$，并记录次数；

当第 $i$ 颗竹子被砍的过程中高度 $x$，存在于第 $i-1$ 颗竹子被砍的过程中，则不计数。

注意： 高度最大值为 $10^{18}$，开方的时候使用 $sqrtl()$ 函数。

C++ 代码

#include 
using namespace std;
typedef long long ll;
#define N 200007

ll ans;
vector vec[N];

ll doIt(ll x) {
	// 数据值过大使用 sqrtl； 
	return sqrtl(x / 2 + 1);
}

int main() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		// 记录第 i 颗竹子高度； 
		ll x;
		cin >> x;
		// 砍第 i 颗竹子； 
		while (x > 1) {
			// 判断第 i 颗竹子砍的过程中，是否与第 i-1 颗存在公共值，默认为 false； 
			bool flag = false;
			for (auto it : vec[i-1])
				// 第 i-1 颗竹子被砍的过程中存在 x 时，flag = true； 
				if (it == x)
					flag = true;
			// 不存在公共值次数加一； 
			if (!flag) ans++;
			// 记录第 i 颗被砍过程中存在的高度； 
			vec[i].push_back(x);
			// 砍竹子； 
			x = doIt(x);
		}
	}
	cout << ans;
	return 0;
} 

---