数据结构与算法学习 01 栈、队列、链表
简介
程序就是数据结构与算法结合后所得到的一个产物。
学习数据结构与算法的好处:
- 代码化繁为简
- 提高代码性能
栈
栈的概念
栈是数据结构中的基础数据结构。
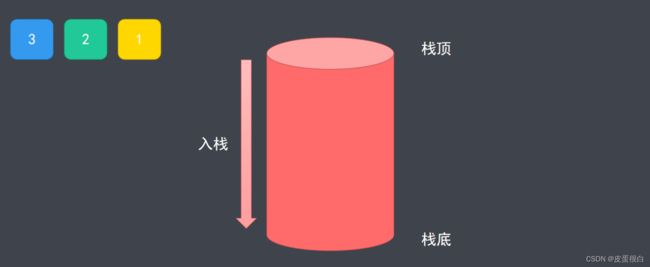
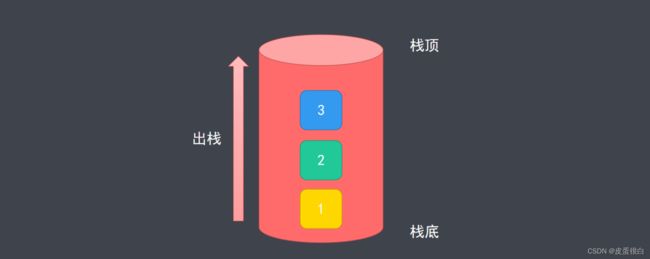
- 栈是一种遵从后进先出原则的有序集合
- 添加新元素的一端称为栈顶,另一端称为栈底
- 操作栈的元素时,只能从栈顶操作(添加、移除或取值)
栈的实现
下面通过 JavaScript 实现栈的功能:
push()入栈方法pop()出栈方法top()获取栈顶值size()获取栈的元素个数clear()清空栈
class Stack {
constructor() {
// 存储栈的数据
this.data = []
// 记录栈的数据个数(相当于数组的 length)
this.count = 0
}
// 入栈
push(item) {
// 方式1:数组方法
// this.data.push(item)
// 方式2:利用数组长度
// this.data[this.data.length] = item
// 方式3:计数方式
this.data[this.count] = item
// 入栈后 count 自增
this.count++
}
// 出栈
pop() {
// 出栈的前提是栈中存在元素,应先行检测
if (this.isEmpty()) {
console.log('栈为空!')
return
}
// 移除栈顶数据
// 方式1:数组方法
// this.data.pop()
// 方式2:计数方式
const temp = this.data[this.count - 1]
delete this.data[--this.count]
return temp
}
// 检测栈是否为空
isEmpty() {
return this.count === 0
}
// 获取栈顶值
top() {
if (this.isEmpty()) {
console.log('栈为空!')
return
}
return this.data[this.count - 1]
}
// 获取元素个数
size() {
return this.count
}
// 清空栈
clear() {
this.data = []
this.count = 0
}
}
const s = new Stack()
s.push('a')
s.push('b')
s.push('c')
console.log(s)
console.log(s.pop())
console.log(s)
console.log(s.top())
console.log(s.size())
s.clear()
console.log(s)
LeetCode 精选题目
包含 min 函数的栈
链接:剑指 Offer 30. 包含min函数的栈
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数,在该栈中,调用 min 、push 及 pop 的时间复杂度都是 O(1)。
示例:
MinStack minStack = new MiStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3
minStack.pop();
minStack.top(); --> 返回 0
minStack.min(); --> 返回 -2
解题思路:
栈的数据结构都是只操作栈顶,所以不存在从栈底或栈中删除元素,因此只需在另一个栈中降序记录 push 过的最小值元素即可。
解题:
// 在存储数据的栈(A)外,再新建一个栈(B),用于存储最小值
class MinStack {
constructor() {
// stackA 用于存储数据
this.stackA = []
this.countA = 0
// stackB 用于将数据降序存储(栈顶值为最小值)
this.stackB = []
this.countB = 0
}
// 入栈
push(item) {
// stackA 正常入栈
this.stackA[this.countA++] = item
// stackB
// 如果没有数据,直接入栈
// 如果 item 的值 <= stackB 的最小值,入栈
if (this.countB === 0 || item <= this.min()) {
this.stackB[this.countB++] = item
}
}
// 最小值函数
min() {
return this.stackB[this.countB - 1]
}
// 获取栈顶值
top() {
return this.stackA[this.countA - 1]
}
// 出栈
pop() {
if (this.countA === 0) {
return
}
// 如果 stackA 的栈顶值 === stackB 的栈顶值,stackB 出栈
if (this.countB > 0 && this.top() === this.min()) {
delete this.stackB[--this.countB]
}
// stackA 出栈
delete this.stackA[--this.countA]
}
}
利用 JS 的内置方法实现上题
使用 JS 内置方法在书写上更加的方便,但是在执行效率上就有所牺牲,因为 JS 内部进行了一些代码的封装,例如 Math.min() 内部也是使用了遍历,而且算法题主要看重的是解题思路,如何更清晰的描述过程是解题的目的。
class MinStack {
constructor() {
this.stack = []
}
// 入栈
push(item) {
this.stack.push(item)
}
// 获取栈顶值
top() {
return this.stack[this.stack.length - 1]
}
// 最小值函数
min() {
return Math.min(...this.stack)
}
// 出栈
pop() {
this.stack.pop()
}
}
每日温度
链接:739. 每日温度
给定一个整数数组 temperatures ,表示每天的气温列表,根据 temperatures 重新生成一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果温度在这之后都不会升高,请在该位置用 0 来代替。
提示:
temperaures的长度范围是[1, 100000]- 温度的值是华氏度,范围是
[30, 100]
示例:
// 示例1
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
// 示例2
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
// 示例3
输入: temperatures = [30,60,90]
输出: [1,1,0]
解题思路:
使用一个存储索引的单调栈,该栈存储的索引对应的温度列表中的温度依次递减;遍历温度列表的索引,依次入栈,每个索引入栈的时候进行判断,如果该温度大于栈顶值对应的温度,则将栈顶值出栈,直到栈顶值对应的温度不小于入栈的温度,最后完成入栈;如果索引在栈中,则表示还未找到下一个更高的温度,如果索引要出栈,则表示已经找到一个比它更高的温度,此时获取两个温度的位置差(索引)就是要等待更高温度的天数。
解题:
/**
* @param {number[]} T 每日温度数组
* @return {number[]} 等待天数列表
*/
var dailyTemperatures = function (T) {
// 创建单调栈用于记录(存储索引值,用于记录天数)
// 初始化第一个索引,表示入栈第一个温度
const stack = [0]
let count = 1
// 创建结果数组(默认将结果数组使用 0 填充)
const len = T.length
const arr = new Array(len).fill(0)
// 遍历 T
for (let i = 1; i < len; i++) {
let temp = T[i]
// 使用 temp 比较栈顶值
// 如果栈顶值小,出栈(计算日期查,并存储),并重复操作
// stack[count - 1] 代表栈顶值
while (count > 0 && temp > T[stack[count - 1]]) {
// 出栈
let index = stack.pop()
count--
// 计算 index 与 i 的差,作为 index 位置的升温日期的天数使用
arr[index] = i - index
}
// 处理完毕,当前温度入栈(等待找到后续的更大温度)
stack.push(i)
count++
}
return arr
}
队列
队列的概念
- 队列是一种遵从先进先出原则的有序集合
- 添加新元素的一端称为队尾,另一端称为队首
队列的实现
基于数组的实现方式
需要实现的功能:
enqueue()入队方法dequeue()出队方法top()获取队首值size()获取队列的元素个数clear()清空队列
class Queue {
constructor() {
// 用于存储队列数据
this.queue = []
}
// 入队
enqueue(item) {
this.queue[this.queue.length] = item
}
// 出队
dequeue() {
if (this.isEmpty()) {
return
}
// 删除 queue 的第一个元素
// delete 会删除索引对应的元素值,但不会删除元素(元素依然占位: undefined),所以不能采取这个方式
// 利用 shift() 删除数组的第一个元素(包括占位)
return this.queue.shift()
}
isEmpty() {
return this.queue.length === 0
}
// 获取队首元素值
top() {
return this.queue[0]
}
size() {
return this.queue.length
}
clear() {
this.queue.length = 0
}
}
const q = new Queue()
q.enqueue(1)
q.enqueue(2)
q.enqueue(3)
console.log(q)
console.log(q.top())
console.log(q.size())
q.dequeue()
console.log(q)
基于对象的实现方式
基于对象的实现方式,摆脱数组内置方法的使用:
class Queue {
constructor() {
this.queue = {}
this.count = 0
// 用于记录队首的 key
this.head = 0
}
// 入队
enqueue(item) {
this.queue[this.count++] = item
}
// 出队
dequeue() {
if (this.isEmpty()) {
return
}
const headData = this.queue[this.head]
delete this.queue[this.head++]
return headData
}
size() {
return this.count - this.head
}
isEmpty() {
return this.size() === 0
}
top() {
return this.queue[this.head]
}
clear() {
this.queue = {}
this.count = 0
this.head = 0
}
}
const q = new Queue()
q.enqueue(1)
q.enqueue(2)
q.enqueue(3)
console.log(q)
console.log(q.size())
q.dequeue()
console.log(q.top())
console.log(q)
双端队列
双端队列(double-ended queue)指的是允许同时从队尾与队首两端进行存取操作的队列,操作更加灵活。
双端队列与 JavaScript 中的数组操作十分相似,只是不允许在数组两端以外的位置进行存取操作。
双端队列的实现
需要实现的新增功能:
addFrount/addBack在首尾两端添加元素removeFront/removeBack从首尾两端移除元素frontTop/backTop获取首尾两端的元素
class Deque {
constructor() {
this.queue = {}
this.count = 0 // 代表队尾索引
this.head = 0 // 代表队首索引
}
// 队首添加
addFront(item) {
// 对象相比数组的好处是可以添加 key 为负数的属性
this.queue[--this.head] = item
}
// 队尾添加
addBack(item) {
// 初始占位是空的,所以先添加在递增 count
this.queue[this.count++] = item
}
// 队首移除
removeFront() {
if (this.isEmpty()) {
return
}
const headData = this.queue[this.head]
delete this.queue[this.head++]
return headData
}
// 队尾移除
removeBack() {
if (this.isEmpty()) {
return
}
const backData = this.queue[this.count - 1]
delete this.queue[--this.count]
return backData
}
// 获取队首
frontTop() {
if (this.isEmpty()) {
return
}
return this.queue[this.head]
}
// 获取队尾
backTop() {
if (this.isEmpty()) {
return
}
return this.queue[this.count - 1]
}
isEmpty() {
return this.size() === 0
}
size() {
return this.count - this.head
}
}
const deq = new Deque()
console.log(deq)
deq.addFront('a')
deq.addFront('b')
deq.addBack('c')
console.log(deq)
console.log(deq.size())
console.log(deq.frontTop())
console.log(deq.backTop())
console.log(deq.removeFront())
console.log(deq.removeBack())
console.log(deq)
LeetCode 精选题目
队列的最大值
链接:剑指 Offer 59 - II. 队列的最大值
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数 max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
解题思路:
通过一个双端队列进行数据的存储,存储的数据保持单调递减的顺序;每次入队一个数据,就和队尾值进行比较,如果小于队尾则从队尾入队,如果大于队尾值则将队尾值进行出队,直到队尾值不小于入队的值,再进行入队操作,这样当前队列的最大值就是这个双端队列的队首值;对当前队列进行出队操作时,只需判断是否与双端队列的队首值相等,如果相等则双端队列执行队首出队操作,如果不相等,只需执行当前队列的出队操作即可。
var MaxQueue = function () {
// 存储队列数据
this.queue = {}
// 双端队列维护最大值(每个阶段的最大值)
this.deque = {}
// 准备队列相关的数据(两个队列的首尾位置)
this.countQ = this.countD = this.headQ = this.headD = 0
}
/** 队尾入队
* @param {number} value
* @return {void}
*/
MaxQueue.prototype.push_back = function (value) {
// 数据再 queue 入队
this.queue[this.countQ++] = value
// 检测是否可以将数据添加到双端队列
// - 队列不能为空
// - value 大于队尾值
while (!this.isEmptyDeque() && value > this.deque[this.countD - 1]) {
// 删除队尾值
delete this.deque[--this.countD]
}
// 将 value 入队
this.deque[this.countD++] = value
}
/** 队首出队
* @return {number}
*/
MaxQueue.prototype.pop_front = function () {
if (this.isEmptyQueue()) {
return -1
}
const headData = this.queue[this.headQ]
// 比较 deque 与 queue 的对手指,如果相同,deque 出队,否则 deque 不操作
if (headData === this.deque[this.headD]) {
delete this.deque[this.headD++]
}
// queue 出队
delete this.queue[this.headQ++]
return headData
}
/** 队列最大值
* @return {number}
*/
MaxQueue.prototype.max_value = function () {
if (this.isEmptyDeque()) {
return -1
}
return this.deque[this.headD]
}
/** 检测队列 queue 是否为空
* @return {boolean}
*/
MaxQueue.prototype.isEmptyQueue = function () {
return this.countQ - this.headQ === 0
}
/** 检测队列 deque 是否为空
* @return {boolean}
*/
MaxQueue.prototype.isEmptyDeque = function () {
return this.countD - this.headD === 0
}
滑动窗口的最大值
链接:239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例:
// 示例1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
// 示例2
输入:nums = [1], k = 1
输出:[1]
范围:
1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
解题思路:
本题与上题【队列的最大值】类似,维护一个单调递减的双端队列,首先初始化窗口大小的队列,依次入队 k 数量的数据;每次入队都和队尾值进行比较,如果小于队尾值则进行入队,否则,队尾值出队,直到队尾值不小于入队的值再执行入队操作;窗口每次移动的时候,进行入队操作,然后对队列中位于窗口外的数据进行出队;队列中存储的可以是数据值也可以是对应数组元素的索引。
/**
* @param {number[]} nums 传入数组
* @param {number} k 滑动窗口的宽度
* @return {number[]} 每次滑动窗口中最大值组成的数组
*/
var maxSlidingWindow = function (nums, k) {
const result = []
const deque = []
/* 1.将窗口第一个位置的数据添加到 deque 中,保持递减 */
for (let i = 0; i < k; i++) {
// - 存在数据
// - 当前数据大于等于队尾值
// - 队尾值出队,再重复比较
while (deque.length && nums[i] >= nums[deque[deque.length - 1]]) {
deque.pop()
}
deque.push(i)
}
// 将第一个位置的最大值添加到 result
result[0] = nums[deque[0]]
/* 2.遍历后续的数据 */
const len = nums.length
for (let i = k; i < len; i++) {
// 同上进行比较
while (deque.length && nums[i] >= nums[deque[deque.length - 1]]) {
deque.pop()
}
deque.push(i)
// 移除窗口外的索引
while (deque[0] <= i - k) {
deque.shift()
}
// 添加最大值到 result
result.push(nums[deque[0]])
}
return result
}
链表
链表的概念
链表是有序的数据结构。
链表与栈、队列的区别是,可以从首、尾以及中间进行数据存取。
为什么不直接使用数组?
这是因为某些操作中,链表的性能要高于数组。
数组在内存中需要占用一段连续的空间,在添加、移除(非最后位置)时会导致后续元素位移,性能开销大。
数组之所以要占用一段连续的内存空间,是为了快速通过索引获取数据,这也是相对链表所具有的优点。
性能测试示例:
const arr = []
console.time('perfText')
for (let i = 0; i < 100000; i++) {
// 从尾部添加不会导致位移
// 耗时:几毫秒
// arr.push(i)
// 从头部添加会导致位移,性能开销大
// 耗时:1秒左右
arr.unshift(i)
}
console.timeEnd('perfText')
由于这种原因,为了减少类似添加、移除操作的性能消耗,可以使用链表这种数据结构。
- 链表是有序的数据结构,链表中的每个部分称为节点
- 链表可以从首、尾以及中间进行数据存取
- 链表的元素在内存中不必是连续的空间
- 优点:添加与删除不会导致其余元素位移
- 缺点:无法根据索引快速定位元素(需要迭代)
使用场景:
- 获取、修改元素时,数组效率高
- 添加、删除元素时,链表效率高
链表的实现
链表的结构:
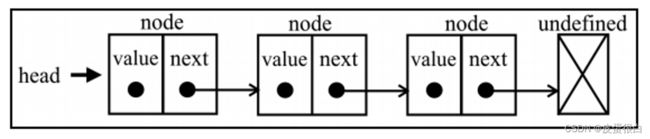
- node 代表链表中的节点,每个节点包含 value 和 next
- value 代表当前节点的数据
- next 代表下一个节点的指针
- head 标记链表的表头,即第一个节点,几乎所有操作都是基于表头进行的
- 链表的最后一个节点的 next 一般对应的 undefined 或 null
需要实现的功能:
- 节点类:value、next
- 链表类:
- addAtTail 尾部添加节点
- addAtHead 头部添加节点
- addAtIndex 指定位置添加节点
- get 获取节点
- removeAtIndex 删除指定节点
// 节点类
class LinkedNode {
constructor(value) {
this.value = value
// 用于存储下一个节点的引用
this.next = null
}
}
// 链表类
class LinkedList {
constructor() {
this.count = 0
this.head = null
}
// 添加节点(尾)
addAtTail(value) {
// 创建新节点
const node = new LinkedNode(value)
// 检测链表是否存在数据
if (this.count === 0) {
this.head = node
} else {
// 找到链表尾部数据,将最后一个节点的 next 设置为 node
let current = this.head
while (current.next !== null) {
current = current.next
}
current.next = node
}
this.count++
}
// 添加节点(首)
addAtHead(value) {
const node = new LinkedNode(value)
if (this.count === 0) {
this.head = node
} else {
// 将 node 添加到 head 的前面
node.next = this.head
this.head = node
}
this.count++
}
// 获取节点(根据索引)
get(index) {
if (this.count === 0 || index < 0 || index >= this.count) {
return
}
// 迭代链表,找到对应节点
let current = this.head
for (let i = 0; i < index; i++) {
current = current.next
}
return current
}
// 添加节点(根据索引)
addAtIndex(value, index) {
if (index >= this.count || index < 0) {
return
}
// 添加到头部
if (index === 0) {
return this.addAtHead(value)
}
// 正常区间处理
const prev = this.get(index - 1)
const node = new LinkedNode(value)
node.next = prev.next
prev.next = node
this.count++
}
// 删除节点(根据索引)
removeAtIndex(index) {
if (this.count === 0 || index < 0 || index >= this.count) {
return
}
if (index === 0) {
this.head = this.head.next
} else {
const prev = this.get(index - 1)
prev.next = prev.next.next
}
this.count--
}
}
链表的多种形式
出了链表的基本形式,还有一些常用的其它形式:
- 双向链表(双端链表)
- 循环链表(环形链表)
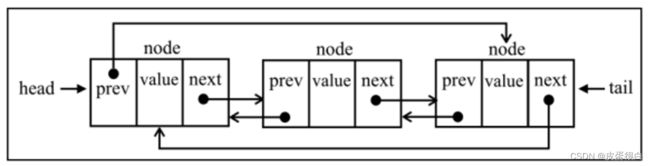
双向链表
双向链表指的是在普通链表的基础上,增加一个用于记录上一个节点的属性 prev,可进行双向访问。
循环链表
循环链表指的是链表最后一个节点的 next 指向第一个节点,形成首尾相连的循环结构。
在实际使用中,不一定是首尾相连,环的结束点可以为链表的任意节点。
LeetCode 精选题目
反转链表
链接:206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
**进阶:**链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
使用迭代方式实现
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function (head) {
// 声明变量记录 prev current
let prev = null
let current = head
// 当 current 是节点时,进行迭代
while(current) {
// 先保存当前节点的下一个节点
const next = current.next
current.next= prev
prev = current
current = next
}
return prev
}
使用递归(循环调用方法自身)方式实现
/**
* @param {ListNode} head 例如 [1,2,3,4,5]
* @return {ListNode}
*/
var reverseList = function (head) {
if (head === null || head.next === null) {
return head
}
const newHead = reverseList(head.next)
// “归”操作
// 能够第一次执行这里的节点为 倒数第二个 节点,即 head 为 4
head.next.next = head
// 当前 head 的 next 需要在下一次“归”操作时赋值
// 当前设置为 null 可以保证第一个节点最终指向 null
head.next = null
// 实际上最终返回的是最后一个节点(即反转后的第一个节点)
return newHead
}
环路检测
链接:面试题 02.08. 环路检测
给定一个链表,如果它是有环链表,实现一个算法返回环路的开头节点。若环不存在,请返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。
示例:
// 示例说明:为了表示给定链表中的环,我们使用整数 `pos` 来表示链表尾连接到链表中的位置(索引从 `0` 开始)。 如果 `pos` 是 `-1`,则在该链表中没有环。注意:`pos` 不作为参数进行传递,仅仅是为了标识链表的实际情况。
// 示例1
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
// 示例2
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
// 示例3
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。
**进阶:**你是否可以不用额外空间解决此题?
使用额外空间
维护一个数组(或 Set 集合),在遍历节点的时候,将节点存储在数组中,每个节点进行数组查询,如果包含该节点,则返回数组索引即可。
空间复杂度 O(n),因为存储了 n 个元素,n 为链表中节点的数目。
不用额外空间
解题思路:快慢指针
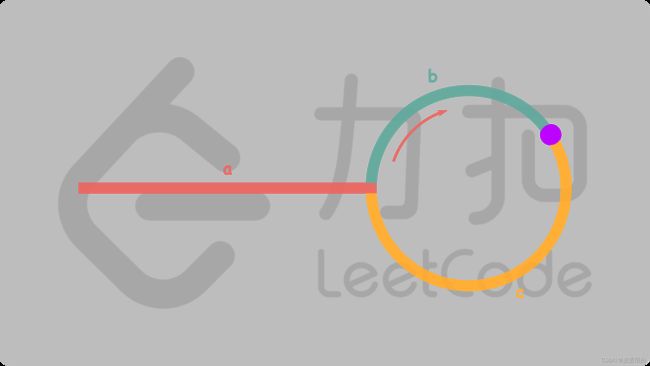
首先使用两个指针 fast 与 slow,它们起始都位于链表头部。随后,slow 指针每次向后移动一个位置,fast 指针向后移动两个位置。如果链表中存在环,则 fast 指针最终会再次与 slow` 指针在环中相遇,即下图中的紫色圆点。这解决了题目的第一个问题。
如下图所示,假设链表中环外部分的长度为 a,slow 指针进入环后,又走了 b 的距离与 fast 相遇。此时 fast 指针已经走完了环的 n 圈,因此 fast 走过的总距离为 a + n(b + c) + b,slow 指针走过的总距离为 a + b。
根据指针的速度,任意时刻,fast 指针走过的距离都为 slow 指针的 2 倍,因此得出 a + n(b + c) + b = 2(a + b),进而得出 a = c + (n - 1)(b + c)。
有了这个公式,我们就会发现:从相遇点到入环点的距离(c),加上 n - 1 圈的环长(环长= b + c),恰好等于从链表头部到入环点的距离,即题目第二个问题的结果。
因此当发现 slow 和 fast 相遇时,再使用一个指针 ptr,它指向链表头部。随后,它和 slow 每次向后移动一个位置。最终它们就会在入环点相遇,此时 ptr 就是环路的开头节点。
事实上 n 的值只能是 1,也就表示 a === c 也是成立的。
空间复杂度 O(1),因为只使用了 slow、fast、ptr 三个指针。
详细参考官方说明的方法二:快慢指针
/**
* @param {ListNode} head
* @return {ListNode} 空节点应为 null
*/
var detectCycle = function (head) {
if (head === null || head.next === null) {
return null
}
// 声明快慢指针
let slow = head
let fast = head
while (fast !== null) {
// 慢指针每次移动一位
slow = slow.next
// 如果 fast 是尾部节点,不存在环
if (fast.next === null) {
return null
}
// 快指针每次移动两位
fast = fast.next.next
// 检测是否有环,快慢指针是否能够相遇
if (slow === fast) {
// 声明新的指针,找到环的开始节点
let ptr = head
// 指针移动直到相遇
while (ptr !== slow) {
ptr = ptr.next
slow = slow.next
}
return ptr
}
}
// while 结束,说明 fast 为 null,说明链表没有环
return null
}