5分钟带你解决智力游戏-----汉诺塔问题

汉诺塔简介：

汉诺塔（Tower of Hanoi），又称河内塔，是一个源于印度古老传说的益智游戏。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。  ---摘自《百度百科》

单独看这样一段话很难理解，我们用数学模型加以解释：

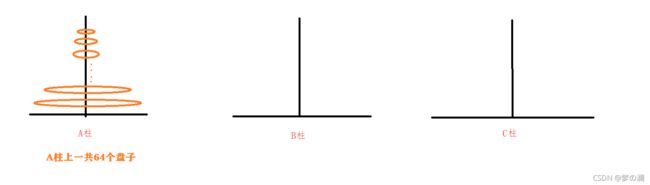
汉诺塔问题可以简化为如何把 A 柱上的 64 个盘子按照 同样的大小顺序 并且每次只能动一个盘子，在每次移动的过程中也要保证大小顺序的情况下转移到 C 柱（可以借助A和B柱）

64个盘子对于我们来说数量过大不好计算它是如何完成的，那我们简化问题

假设 1 ： A 柱上就 一个盘子 我们应该如何转移到 C 柱上呢？

我们可以直接把这个盘子从A转移到C上就大功告成了！！！

步骤：A->C 一共是一步完成的转移

假设 2 ： A 柱上就 两个盘子 我们应该如何转移到 C 柱上呢？

我们可以把最上面的盘子先转移到 B 柱上，然后最下面的盘子转移到 C 柱，最后把 B 柱的盘子转移到 C 柱就完成了，图解如下： 

 我们可以看到转移的步骤是：A->B   A->C   B->C 一共是三步完成的

假设 3 ： A 柱上就 三个盘子 我们应该如何转移到 C 柱上呢？

步骤较多我们用图例来进行解释：

❗️ 切忌在转移过程中也要保证大小顺序！！！

 

 

步骤：A——>C A——>B C——>B A——>C B——>A B——>C A——>C 一共是七步 

综上三种情况我们可以用数学归纳法得出结论：

当一个盘子时：需要一步

当两个盘子时：需要三步

当三个盘子时：需要七步

所以：我们发现盘子的个数和转移的步数存在关系！！！

盘子个数我们设为 n， 步数为 x

即：x = 2^n - 1

  那我们思考一个问题：那 64 个盘子需要多少步：2^64-1步

嗯……………………大概就是这么多步

我们假设一个问题：如果要是人计算的话需要多长时间：如果一个人都是在 1s 内完全正确的摆放

  嗯……………………大概就是这么多年

❓ 如果计算机计算呢？？？

博主的计算机是：2.1GHZ的

 

  嗯……………………大概就是这么多年，不过欣慰的是少了蛮多年的，就200多年

---

❗️下面我们来看一下实现汉诺塔的代码：

这里我采用Java实现：

public class TestDemo {
    /**
     * 在这里传入两个需要移动的坐标
     * @param pos1
     * @param pos2
     */
    public static void move(char pos1, char pos2){
        System.out.print(pos1+"——>"+pos2+" ");
    }
    public static void hannotta(int n, char pos1, char pos2, char pos3){
        if(n==1){
            move(pos1,pos3);
        }
        else{
            hannotta(n-1,pos1,pos3,pos2);
            move(pos1,pos3);
            hannotta(n-1,pos2,pos1,pos3);
        }
    }
    public static void main(String[] args) {
        hannotta(1,'A','B','C');
        System.out.println();
        hannotta(2,'A','B','C');
        System.out.println();
        hannotta(3,'A','B','C');
    }
}

A——>C 
A——>B A——>C B——>C 
A——>C A——>B C——>B A——>C B——>A B——>C A——>C 

 ❗️ 代码解析：

我们在这里采用的是递归的思想，该代码递归本身展开后十分复杂，所以这里只说明递归的思想，展开的计算就交给计算机来计算

我们参考上面三个转移的假设，我们可以借助3个盘子的案例得出一个结论：③号盘子在转移的前几步是不动的，是①和②号盘子先进行移动的，①和②的起始位置都是A柱，目及地都是B柱，途中①在C柱有一步中转，所以由于①和②的起始位置以及目及地都是相同的，所以把除去最底层的③号盘剩余的盘子看做一个整体（①和②看做整体），在③转移到C柱后，由①②组成的整体以B柱作为起始位置，C作为目及地途中①会在A柱中转一次，通过分析我们三个盘子的案例我们把这个规律应用到64盘子的案例

64个盘子：先把除去64号盘子剩余的63个盘子看做一个整体，此整体的起始位置是A柱，会有部分单体需要在C柱进行中转，目及地是B柱，待64号盘子转移到C柱后，整体以B柱作为起始位置，部分单体需要在A柱进行中转，C柱作为整体的目及地，每次完成转移后整体数-1，直到整体数为1遇到递归的终止条件，把最后一个盘子由A转移转移到C程序结束，这样就完成了我们所有的盘子按照汉诺塔规则的转移

图解：

⭐️逐语句解析：

1️⃣ 这里调用 hannotta 方法去打印步骤，传入盘子数量以及ABC三个柱，每打印一种情况的步骤换一次行

 public static void main(String[] args) {
        hannotta(1,'A','B','C');
        System.out.println();
        hannotta(2,'A','B','C');
        System.out.println();
        hannotta(3,'A','B','C');
    }

2️⃣ 写一个 move 方法模拟盘子移动的步骤：

 public static void move(char pos1, char pos2){
        System.out.print(pos1+"——>"+pos2+" ");
    }

3️⃣ hannotta实现汉诺塔的方法，这里pos1，pos2，pos3分别是A,B,C柱。方法的第一个参数（pos1）是起始位置，第二个参数（pos2）是中转位置，第三个参数（pos3）是目及地。进来先判断如果只有一个盘子，直接由 A 柱转移到 C 柱。如果盘子的总数 n 大于1，就先把 n-1 个盘子看做整体，按照我们上面说的方法进行移动 

   public static void hannotta(int n, char pos1, char pos2, char pos3){
        if(n==1){
            move(pos1,pos3);
        }
        else{
            hannotta(n-1,pos1,pos3,pos2);
            move(pos1,pos3);
            hannotta(n-1,pos2,pos1,pos3);
        }
    }

那我们运行一下64个盘子的案例：

hannotta(64,'A','B','C');

 截取了一部分运行结果，200年后差不多就可以看见所有的步骤啦

---

这就是汉诺塔的解决办法，代码虽然简单，但是对于不熟悉递归思想的同学有些难，希望本篇文章可以对大家有所帮助！！！如果本篇文章对你有所帮助，还请大家一键三连，谢谢支持！！