（pytorch进阶之路）cGAN、LSGAN

原来gan有什么问题：判别器的输入无论是真实的样本还是预测样本，输入都只有一个，x或者g(z)，我们只是把照片放入判别器中

但是我们在MNIST数据集中，有10类数据分别是0~9，仅仅是输入随机的高斯变量z，没有输入任何的其他信息，不能指望生成器能够生成特定数字照片

cGAN

原先的随机高斯变量随机性和不确定度很大，有帮助于预测目标照片的信息特别少，这时候我们能提供一个变量c（condition条件），也就是G不仅仅输入z，还输入c，这个c可以是个标签信息，更好的指导生成特定数字的照片

论文地址：
https://arxiv.org/pdf/1411.1784

公式：y可能是每张照片的标签信息

y作为判别器和生成器的输入时，更好的去学习目标照片

绿色部分就是条件信息，可以是离散或者连续的变量，常见做法像是MNIST的one-hot label转化成类似word emb，再和z拼接起来输入道网络之中

基于GAN修改代码，
对于generator，forward函数加多一个参数labels，传入nn.Embedding获取emb，再和z拼接即可，修改一下DNN网络，第一层的DNN第一个参数改成(in_dim + label_emb_dim）

import torch
import torch.nn as nn
import torch.utils.data
import numpy as np


class CGenerator(nn.Module):
    def __init__(self, latent_dim, image_size: list, cls_num, label_emb_dim):
        """
        image_size = [1, 28, 28]
        """
        super().__init__()
        self.image_size = image_size
        self.embedding = nn.Embedding(cls_num, label_emb_dim)
        out_dim = int(np.prod(image_size))
        self.model = nn.Sequential(
            torch.nn.utils.spectral_norm(nn.Linear(latent_dim + label_emb_dim, 64)),
            nn.ReLU(inplace=True),
            torch.nn.utils.spectral_norm(nn.Linear(64, 128)),
            nn.ReLU(inplace=True),
            torch.nn.utils.spectral_norm(nn.Linear(128, 256)),
            nn.ReLU(inplace=True),
            torch.nn.utils.spectral_norm(nn.Linear(256, 512)),
            nn.ReLU(inplace=True),
            torch.nn.utils.spectral_norm(nn.Linear(512, 1024)),
            nn.ReLU(inplace=True),
            torch.nn.utils.spectral_norm(nn.Linear(1024, out_dim)),
            nn.Tanh()
        )

    def forward(self, z, labels):
        """
        labels: 标签信息，离散的标签变量
        z: noise, shape = [bs, latent_dim]
        return:
            image.shape = [bs, c, h, w]
        """
        label_emb = self.embedding(labels)
        print(label_emb.shape)
        z = torch.cat([z, label_emb], dim=-1)

        output = self.model(z)
        images = output.reshape([z.shape[0], *self.image_size])
        return images


def test_main():
    bs, c, h, w = 2, 1, 28, 28
    image_size = [c, h, w]
    latent_dim = 64
    inputx = torch.randn([bs, latent_dim])
    cls_num = 10
    label_emb_dim = 32
    labels = torch.randint(0, 9, [bs, ])
    res = CGenerator(latent_dim, image_size, cls_num, label_emb_dim)(inputx, labels)
    print(res.shape)


if __name__ == '__main__':
    test_main()

同理对于discriminator，forward函数加多一个参数labels，传入nn.Embedding获取emb，再和z拼接，同理修改DNN网络第一层DNN第一个参数输入dim大小

import torch
import torch.nn as nn
import numpy as np


class CDiscriminator(nn.Module):
    def __init__(self, image_size: list, cls_num, label_emb_dim):
        """
        image_size: list = [c, h, w]
        """
        super().__init__()
        self.image_size = image_size
        self.embedding = nn.Embedding(cls_num, label_emb_dim)

        in_dim = int(np.prod(image_size))
        self.model = nn.Sequential(
            nn.Linear(in_dim + label_emb_dim, 1024),
            nn.ReLU(inplace=True),
            nn.Linear(1024, 512),
            nn.ReLU(inplace=True),
            nn.Linear(512, 256),
            nn.ReLU(inplace=True),
            nn.Linear(256, 128),
            nn.ReLU(inplace=True),
            nn.Linear(128, 64),
            nn.ReLU(inplace=True),
            nn.Linear(64, 1),
            # 输出是个sigmoid概率 0~1
            nn.Sigmoid()
        )

    def forward(self, images, labels):
        """
        images.shape = [bs, c , h , w]
        return:
            probability.shape = [bs, 1]
        """
        labels_emb = self.embedding(labels)
        inputx = torch.cat([images.reshape(images.shape[0], -1), labels_emb], dim=-1)
        probability = self.model(inputx)
        return probability


def test_main():
    bs, c, h, w = 2, 1, 28, 28
    d = CDiscriminator([c, h, w], 10, 32)
    labels = torch.randint(0, 9, [bs, ])
    inputx = torch.randn([bs, c, h, w])
    prob = d(inputx, labels)
    print(prob.shape)


if __name__ == '__main__':
    test_main()

LSGAN

Least Squares GAN，最小二乘GAN/最小平方GAN，目前很多GAN的论文或者代码已经不再是原始的GAN所用的二元交叉熵目标函数了，很多采用的是LSGAN的目标函数，类似做一个回归任务，而不是分类任务

原始GAN是用sigmoid的交叉熵误差函数，但是这种目标函数可能会导致梯度消失的问题，loss曲线当x大于2时loss的斜率已经接近于0，优化二元交叉熵函数相当于在优化JSD散度（Jensen–Shannon divergence）

LSGAN采用的是最小平方误差函数，最小化最小平方误差函数相当于优化一个Pearson卡方散度，LSGAN能产生更高质量的图片，在训练过程中会更加的稳定

论文地址：
https://openaccess.thecvf.com/content_ICCV_2017/papers/Mao_Least_Squares_Generative_ICCV_2017_paper.pdf

假设我们使用的编码方案为
虚假标签定义为：a
真实标签定义为：b，
用c表示G想要D相信的虚假信息的值

我们LSGAN的目标函数：只用一个回归的值去表示

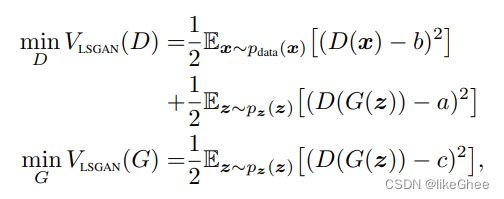
当b-c=1，b-a=2时，2C(G) = pearson卡方散度形式
比如：a=-1，b=1，c=0

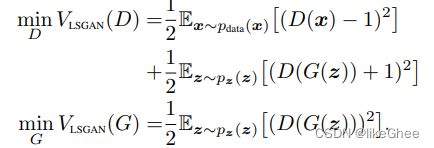
另一种方案是让G生成样本尽可能和真实样本一致，c=b=1，a=0

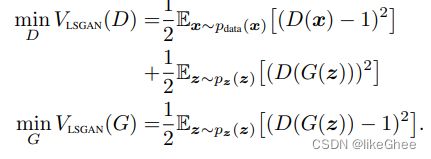
代码实现，原先使用的BCE loss，换成MSE loss，
loss_fn = torch.nn.MSELoss()

真实标签设为1，虚假标签设为0和之前设的为一致，就不用动了