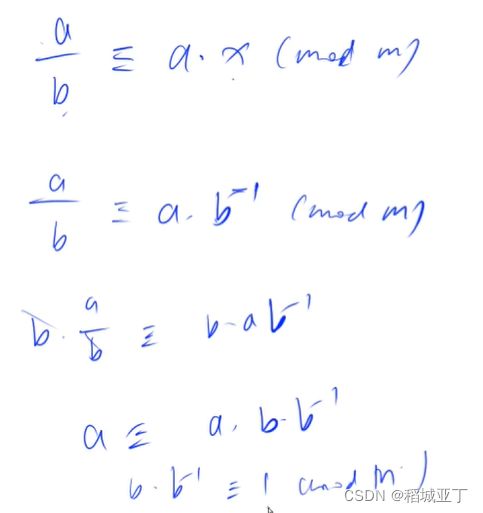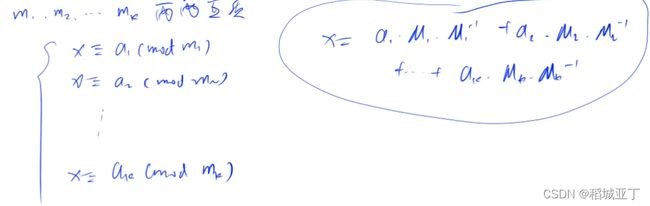数学知识(二):欧拉函数、快速幂、扩展欧几里得算法、中国剩余定理
欧拉函数
公式法求欧拉函数
基本原理:O(n√ai)
例题:欧拉函数
给定 n个正整数 ai,请你求出每个数的欧拉函数。
欧拉函数的定义
1∼N中与 N 互质的数的个数被称为欧拉函数,记为 ϕ(N)
若在算数基本定理中,N=pa11pa22…pamm,则:
ϕ(N) = N×p1−1p1×p2−1p2×…×pm−1pm
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个正整数 ai。
输出格式
输出共 n 行,每行输出一个正整数 ai的欧拉函数。
数据范围
1≤n≤100
1≤ai≤2×109
输入样例:
3
3
6
8
输出样例:
2
2
4解题代码:
#include
#include
using namespace std;
int main()
{
int n;
cin >>n;
while(n--)
{
int a;
cin>>a;
int res=a;
for(int i=2;i<=a/i;i++)//分解质因数
if(a%i==0)//a是i的质因子
{
res=res/i*(i-1);//公式
while(a%i==0) a/=i;//把i除干净
}
if(a>1) res=res/a*(a-1);
cout< 筛法求欧拉函数
例题:
给定一个正整数 n,求 1∼n中每个数的欧拉函数之和。
输入格式
共一行,包含一个整数 n。
输出格式
共一行,包含一个整数,表示 1∼n中每个数的欧拉函数之和。
数据范围
1≤n≤106
输入样例:
6
输出样例:
12解题代码:
#include
#include
using namespace std;
typedef long long LL;
const int N=1000010;
int primes[N],cnt;//primes存的是每一个质数,cnt存的是质数的下标
bool st[N];//表示是否被筛掉了
int phi[N];//欧拉函数
LL get_eulers(int n)
{
phi[1]=1;
for(int i=2;i<=n;i++)//线性筛法
{
if(!st[i])
{
primes[cnt++]=i;
//如果是质数
phi[i]=i-1;
}
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=true;//每次把当前的质数与i的乘积筛掉
if(i%primes[j]==0)
{
phi[primes[j]*i]=primes[j]*phi[i];
break;
}
phi[primes[j]*i]=phi[i]*(primes[j]-1);
}
}
LL res=0;
for(int i=1;i<=n;i++) res+=phi[i];
return res;
}
int main()
{
int n;
cin>>n;
cout< 欧拉函数作用:
欧拉定理证明:
费马定理
快速幂
例题:快速幂
给定 n 组 ai,bi,pi,对于每组数据,求出 abii mod pi的值。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含三个整数 ai,bi,pi
输出格式
对于每组数据,输出一个结果,表示 abii mod pi的值。
每个结果占一行。
数据范围
1≤n≤100000
1≤ai,bi,pi≤2×109
输入样例:
2
3 2 5
4 3 9
输出样例:
4
1解题代码:
#include
#include
using namespace std;
typedef long long LL;
//求a^b % p
LL qmi(int a, int b, int p)
{
LL res = 1 % p;
while (b)
{
if (b & 1) res = res * a % p;//%p防止溢出
a = a * (LL)a % p;
b >>= 1;//把b的末位删除
}
return res;
}
int main()
{
int n;
scanf("%d", &n);
while (n -- )
{
int a, b, p;
scanf("%d%d%d", &a, &b, &p);
printf("%lld\n", qmi(a, b, p));
}
return 0;
}
例题:快速幂求逆元
给定 n 组 ai,pi,其中 pi 是质数,求 ai模 pi 的乘法逆元,若逆元不存在则输出 impossible。
注意:请返回在 0∼p−1之间的逆元。
乘法逆元的定义
若整数 b,m互质,并且对于任意的整数 a,如果满足 b|a,则存在一个整数 x,使得 a/b≡a×x(modm)则称 x为 b 的模 m 乘法逆元,记为 b−1(modm)
b 存在乘法逆元的充要条件是 b 与模数 m 互质。当模数 m 为质数时,bm−2 即为 b 的乘法逆元。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一个数组 ai,pi,数据保证 pi 是质数。
输出格式
输出共 n 行,每组数据输出一个结果,每个结果占一行。
若 ai 模 pi 的乘法逆元存在,则输出一个整数,表示逆元,否则输出 impossible。
数据范围
1≤n≤105
1≤ai,pi≤2∗109
输入样例:
3
4 3
8 5
6 3
输出样例:
1
2
impossible解题思路:
解题代码:
#include
#include
using namespace std;
typedef long long LL;
//求a^b % p
LL qmi(int a, int b, int p)
{
LL res = 1 % p;
while (b)
{
if (b & 1) res = res * a % p;//%p防止溢出
a = a * (LL)a % p;
b >>= 1;//把b的末位删除
}
return res;
}
int main()
{
int n;
scanf("%d", &n);
while (n -- )
{
int a, p;
scanf("%d%d%", &a, &p);
LL res=qmi(a, p-2, p);
if(a%p) printf("%lld\n", res);
else puts("impossible");
}
return 0;
}
扩展欧几里得算法
裴蜀定理:
对于任意正整数a,b,一定存在非零整数x,y,使得 :
ax+by=(a,b)//(a,b)是a、b的最大公约数的倍数
即a,b能凑出的最小的正整数,就是其最大公约数
扩展欧几里得算法就是来求它们的系数的,即x,y
例题:扩展欧几里得算法
给定 n 对正整数 ai,bi,对于每对数,求出一组 xi,yi使其满足 ai×xi+bi×yi=gcd(ai,bi)
输入格式
第一行包含整数 n。
接下来 n 行,每行包含两个整数 ai,bi
输出格式
输出共 n 行,对于每组 ai,bi求出一组满足条件的 xi,yi每组结果占一行。
本题答案不唯一,输出任意满足条件的 xi,yi 均可。
数据范围
1≤n≤105
1≤ai,bi≤2×109
输入样例:
2
4 6
8 18
输出样例:
-1 1
-2 1解题代码:
#include
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
if(!b)
{
x=1,y=0;
return a;
}
int d= exgcd(b,a%b,y,x);
y-=a/b *x;
return d;
}
int main()
{
int n;
scanf("%d",&n);
while(n --)
{
int a,b,x,y;
scanf("%d%d",&a,&b);
exgcd(a,b,x,y);
printf("%d %d\n",x,y);
}
return 0;
} 运用:求解线性同余方程
给定 n 组数据 ai,bi,mi对于每组数求出一个 xi,使其满足 ai×xi≡bi(mod mi)如果无解则输出 impossible。
输入格式
第一行包含整数 n。
接下来 n 行,每行包含一组数据 ai,bi,mi
输出格式
输出共 n 行,每组数据输出一个整数表示一个满足条件的 xi,如果无解则输出 impossible。
每组数据结果占一行,结果可能不唯一,输出任意一个满足条件的结果均可。
输出答案必须在 int 范围之内。
数据范围
1≤n≤105
1≤ai,bi,mi≤2×109
输入样例:
2
2 3 6
4 3 5
输出样例:
impossible
-3解题:
中国剩余定理
例题:表达整数的奇怪方式
给定 2n 个整数 a1,a2,…,an 和 m1,m2,…,mn求一个最小的非负整数 x,满足 ∀i∈[1,n],x≡mi(mod ai)
输入格式
第 1 行包含整数 n。
第 2…n+1 行:每 i+1 行包含两个整数 ai 和 mi,数之间用空格隔开。
输出格式
输出最小非负整数 x,如果 x 不存在,则输出 −1。
如果存在 x,则数据保证 x 一定在 64 位整数范围内。
数据范围
1≤ai≤231−1
0≤mi
输入样例:
2
8 7
11 9
输出样例:
31解题:
#include
#include
using namespace std;
typedef long long LL;
LL exgcd(LL a,LL b,LL &x,LL &y)
{
if(!b)
{
x=1,y=0;
return a;
}
LL d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
int n;
cin >>n;
bool has_answer =true;
LL a1,m1;
cin>>a1>>m1;
for(int i=0;i>a2>>m2;
//求出k1,k2的值
LL k1,k2;
LL d=exgcd(a1,a2,k1,k2);
//该方程有解
if((m2-m1)%d)
{
has_answer=false;
break;
}
//k1,k2 翻倍成m1,m2
k1*=(m2-m1)/d;
LL t=a2/d;//先将数存下来
k1=(k1%t+t)%t;//将k1变成方程的最小正整数解
m1=a1*k1+m1;
a1=abs(a1/d*a2);
}
if(has_answer)
{
cout<<(m1%a1+a1)%a1 <