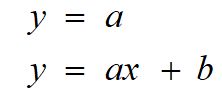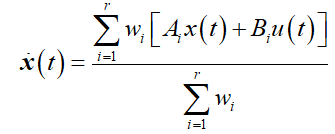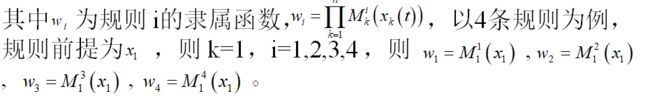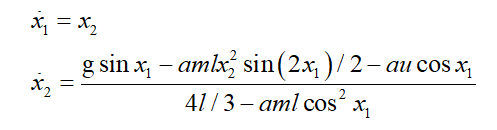1、Sugeno模糊模型
传统的模糊系统为Mamdani模糊模型,输出为模糊量。
Sugeno模糊模型输出隶属函数为constant或linear,其函数形式为:
它与Mamdani模型的区别在于:
(1)输出变量为常量或线性函数;
(2)输出为精确量。
2 、仿真实例
设输入X∈[0,5] 和Y∈[0,10] ,将它们模糊化为两个模糊量:小,大。输出Z为输入(X,Y)的线性函数,模糊规则为:
3、基于T-S(Takagi-Sugeno)模型的模糊控制
针对 n个状态变量 m个控制输入的连续非线性系统,其T-S型模糊模型可描述为以下 r条模糊规则:
根据模糊系统的反模糊化定义,由模糊规则构成的模糊模型总的输出为:
4、单级倒立摆的T-S模型模糊控制
倒立摆系统的控制问题一直是控制研究中的一个典型问题。控制的目标是通过给小车底座施加一个力 u(控制量),使小车停留在预定的位置,并使摆不倒下,即不超过一预先定义好的垂直偏离角度范围。单级倒立摆模型为:
其中 x1为摆的角度, x2为摆的角速度,2l为摆长,u为加在小车上的控制输入,a=1/(M+m) ,M 和m 分别为小车和摆的质量。
基于2条模糊规则的设计
根据倒立摆的两条T-S模糊模型规则,隶属函数应按图4-29进行设计。仿真中采用三角形隶属函数实现摆角度x1(t)的模糊化。选择期望的闭环极点(-3-3i,-3+3i) ,利用极点配置函数place(A,B,P),可以得到系统的反馈增益矩阵:K1=[-418 -74] ,K2=[-10452 -2292] 。 采用 ui=-Kix的反馈控制,按式(4.16)设计控制器.
基于4条模糊规则的设计