upc 个人训练赛第七场:最佳课题选择(dp)
问题 A: 本材加工
题目描述
2049年,智能机器人在各行各业中的应用已经十分普遍了,小明的运输队里就有一个,是专门用来装卸货物的。这天,他们的任务是要把N(2≤N≤50)根木材运送到家具厂去。这些木材长短不同(有擎还特别的长),为了便于运输,只好把它们切割成小段。所以,小明给机器人的任务是:把这些木材切割并装上卡车。等机器人做完这事的时候,小明一看结果,大吃一谅:原来装在车上的所有小段的木材,居然长度都是一样的(以米为单位),而且,还是所有可行方案中,切割次数最少的那种方案!
如果告诉你最开始那N根本材的长度,你能算出机器人切割出的小段的长度吗?
输入
第一行有一个整数N,表示原始木材的数量。第二行中是N个用空格分开的整数,表示每根木材的长度(以米为单位),已知这些整数不小于1,不超过400000。
输出
只有一个整数,表示机器人切割出来的每个小段的长度。
样例输入 Copy
4
4 22 8 12
样例输出 Copy
2
思路:
求n个数的最大公约数
int n,ans;
int a[55];
int GCD(int a[])
{
ans = a[0];
for(int i=1;i<n;i++)
ans = gcd(ans,a[i]);
return ans;
}
int main()
{
cin >> n;
for(int i=0;i<n;i++) cin >> a[i];
GCD(a);
cout << ans << endl;
return 0;
}
问题 B: 螺旋矩阵
题目描述
输入一个正整数N(1≤N≤20)后 ,可以得到一个N×N的数字螺旋方阵,先分别求出该方阵中的主对角线与副对角线上的数字之和S,P,然后输出S和P的积。
例如,N=5时得到的数字螺旋方阵如下 :
其中:主对角线从左上角到右下角,得到的数字之和S=1+17+25+21+9=73。副对角线从右上角到左下角,得到的数宇之和 P=5+19+25+23+13=85。
最后S*P=6205
输入
只有一行,一个正整数N。
输出
只有一行,一个正整数(表示主对角线与副对角线上的数字之和的积)
样例输入 Copy
5
样例输出 Copy
6205
思路:
写一个螺旋矩阵出来,然后分别计算主副对角线的和,最后相乘即可
int a[22][22];
int n,x,y,tot;
ll s,p,ans;
int main()
{
n = read();
memset(a,0,sizeof a);
x = 0,y = n-1;
tot = a[x][y] = 1;
while(tot < n*n)//构造螺旋矩阵
{
while(x+1<n && !a[x+1][y]) a[++x][y] = ++tot;
while(y-1>=0 && !a[x][y-1]) a[x][--y] = ++tot;
while(x-1>=0 && !a[x-1][y]) a[--x][y] = ++tot;
while(y+1<n && !a[x][y+1]) a[x][++y] = ++tot;
}
for(int i=0;i<n;i++){
s += a[i][i];
}
for(int i=0;i<n;i++){
p += a[i][n-i-1];
}
ans = s*p;
cout << ans << endl;
return 0;
}
问题 C: 懒羊羊吃草
题目描述
众所周知,懒羊羊是所有小羊里最贪吃的一只。然而,鲜为人知的是,懒羊羊也有存储粮食的习惯。而更让大家吃惊的事实是,我们的懒羊羊做事很有条理,每当他存储一份粮食时,他会专门拿出一个筐来存放。因此,他的仓库里有很多很多筐的青草。而我们的懒羊羊又是一个经常馋嘴的小羊,每当他想吃草时,就会从仓库里找出数量最少的一筐草,把它吃掉。可是懒羊羊因为草吃得太多了导致大脑运转缓慢,所以他不得不向你请求支援,帮他找出他应该吃数量为多少的青草。
输入
第一行为一个正整数n,表示懒羊羊一共进行了n次操作(2<=n<=1000000)
第二行至第n+1行每行表示一个懒羊羊的操作,当这行形式为单独一个字符‘q’时,表示懒羊羊肚子饿了,要吃掉仓库里当前数量最少的那份青草;当这行形式为一个字符‘ i’和一个整数k时,表示懒羊羊将一份数量为k(1<=k<=2147483647)的青草存入了仓库,‘ i’和k之间用空格隔开。
输入数据保证每次询问时仓库里都有草可吃且所有操作中懒羊羊至少会吃一次草。
输出
每当输入为‘q’时,输出懒羊羊当前吃掉的那份青草的数量是多少。
样例输入 Copy
5
i 5
i 2
q
i 9
q
样例输出 Copy
2
5
提示
30%数据满足1<=p<=3000;
60%数据满足1<=p<=40000;
100%数据满足1<=p<=1000000.
思路:
根据题意模拟即可,个人感觉用优先队列会更好
priority_queue<int,vector<int>,greater<int> >q1;//小
int n,k;
char c;
int main()
{
n = read();
while(n--)
{
cin >> c;
if(c == 'i')
{
k = read();
q1.push(k);
}
if(c == 'q')
{
printf("%d\n",q1.top());
q1.pop();
}
}
return 0;
}
问题 D: 找分数
题目描述
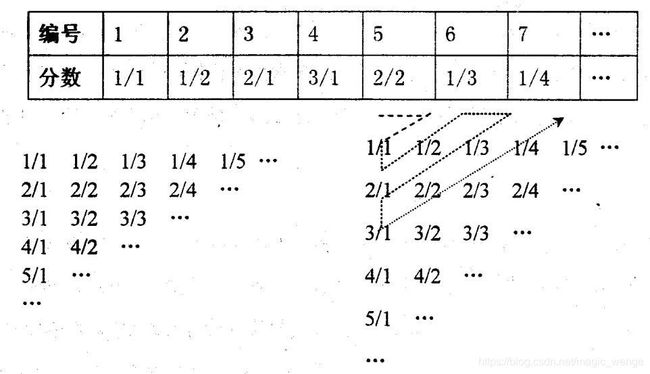
有一张分数表,其中的每一项是以“Z”字形先后次序按某种规律形成的,每一项编号和对应的分数如下表和下图所示:
请根据表中规律,对于输入的整数N(1≤N≤20000),输出对应的第N项分数。
输入
只有一行,一个正整数N。
输出
只有一行,一个分数,分子和分母间用“/”号分隔。
样例输入 Copy
8
样例输出 Copy
2/3
思路:
观察之后不难发现,分数线左右的两个数的和是相等的
int n;
int main()
{
n = read();
int i = 0;
while(i < n){
n = n-i;i = i+1;
}
if(i%2 == 0){
printf("%d/%d\n",n,i+1-n);
}
else
printf("%d/%d\n",i+1-n,n);
}
问题 E: 最佳课题选择
题目描述
Matrix67要在下个月交给老师n篇论文,论文的内容可以从m个课题中选择。由于课题数有限,Matrix67不得不重复选择一些课题。完成不同课题的论文所花的时间不同。具体地说,对于某个课题i,若Matrix67计划一共写x篇论文,则完成该课题的论文总共需要花费Ai * x^Bi个单位时间(系数Ai和指数Bi均为正整数)。给定与每一个课题相对应的Ai和Bi的值,请帮助Matrix67计算出如何选择论文的课题使得他可以花费最少的时间完成这n篇论文。
输入
第一行有两个用空格隔开的正整数n和m,分别代表需要完成的论文数和可供选择的课题数。
以下m行每行有两个用空格隔开的正整数。其中,第i行的两个数分别代表与第i个课题相对应的时间系数Ai和指数Bi。
输出
输出完成n篇论文所需要耗费的最少时间。
样例输入 Copy
10 3
2 1
1 2
2 1
样例输出 Copy
19
提示
样例解释
4篇论文选择课题一,5篇论文选择课题三,剩下一篇论文选择课题二,总耗时为24 ^ 1 + 11 ^ 2 + 2 * 5^1 = 8+1+10 = 19。可以证明,不存在更优的方案使耗时小于19。
对于100%的数据,n<=200,m<=20,Ai<=100,Bi<=5。
ll m,n;
ll f[1001],a[1001],b[1001],c[1001][1001];
ll init(ll x,ll t)
{
ll s = 1;
for(int i=1;i<=t;i++) s *= x;
return s;
}
int main()
{
memset(f,127/3,sizeof(f));
cin >> m >> n;
for(int i=1;i<=n;i++) cin >> a[i] >> b[i];
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
c[i][j] = a[i]*init(j,b[i]);
}
}
f[0] = 0;
for(int i=1;i<=n;i++)
for(int k=m;k>=0;k--)
for(int j=1;j<=k;j++)
{
f[k] = min(f[k],f[k-j]+c[i][j]);
}
printf("%lld\n",f[m]);
return 0;
}