基于 Bounding Box 的弱监督实例分割 BoxSnake: Polygonal Instance Segmentation with Box Supervision 论文笔记
基于 Bounding Box 的弱监督实例分割 BoxSnake: Polygonal Instance Segmentation with Box Supervision 论文笔记
- 一、Abstract
- 二、引言
- 三、相关工作
-
- 基于 Mask 的实例分割
- 基于多边形的实例分割
- 基于 Box 的弱监督实例分割
- 四、BoxSnake
-
- 4.1 定义
- 4.2 基于点的一元损失
- 4.3 距离感知的成对损失
-
- 局部成对
- 全局成对
- 裁剪策略
- 4.4 网络结构
- 五、实验
-
- 5.1 实施细节
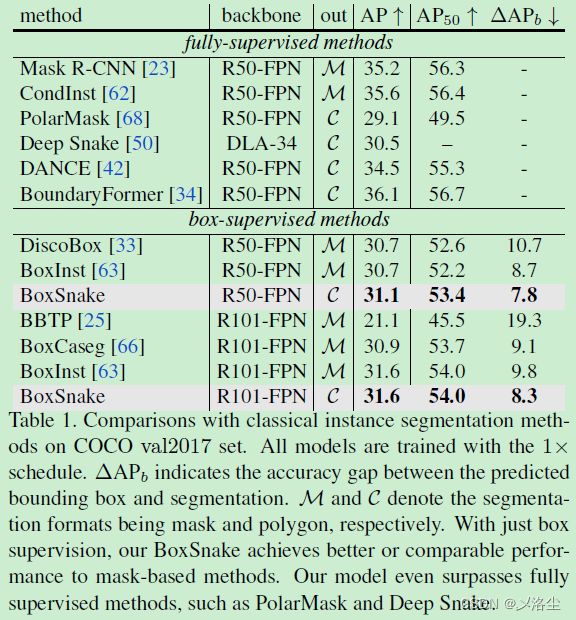
- 5.2 主要结果
-
- COCO 的结果
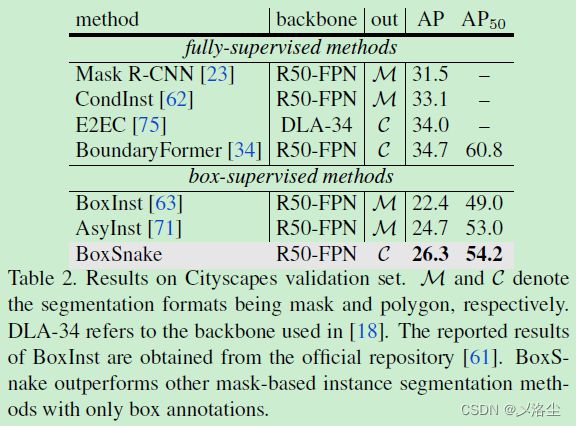
- Cityscapes 的结果
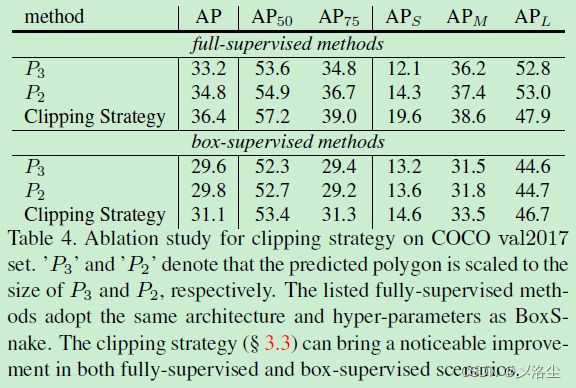
- 5.3 消融实验
-
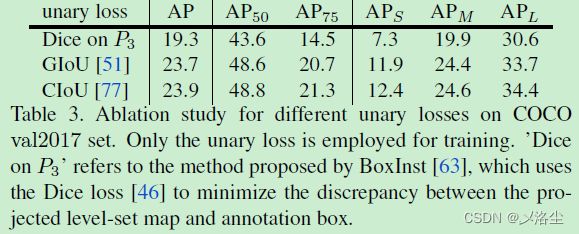
- 不同的一元损失
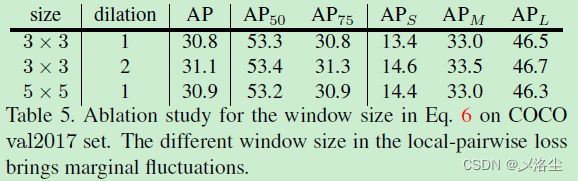
- 窗口尺寸的改变
- 裁剪策略的有效性
- 不同的初始化方法
- 每个损失的效果
- 更大的 Backbone
- 六、结论
- A、关于距离放缩的细节
- B、附加的消融实验
-
- B.1 成对损失的权重
- B.2 距离放缩的温度
- C、可视化
写在前面
又是新一周的开始,冲冲冲~
- 论文地址:BoxSnake: Polygonal Instance Segmentation with Box Supervision
- 代码地址:https://github.com/Yangr116/BoxSnake,暂时只有个仓库,完整代码尚未放出~
- 预计投稿在三大顶会,不知结果如何~
- 2023 每周一篇博文,欢迎关注,主页更多干货,持续助力科研~
一、Abstract
最近基于 Box 监督的实例分割很火,但目前的方法主要依赖基于 mask 的框架,本文首次提出基于 polygonal 多边形的分割。模型由两部分组成:基于点的一元损失,用于限制预测的多边形所形成的 bounding box,从而实现粗分割;距离感知成对损失,用于促进预测的多边形拟合目标轮廓。相比于 mask 的弱监督方法,本文提出的 BoxSnake 在 COCO 和 Cityscapes 数据集上更有效。
二、引言
首先指出实例分割的意义。目前有两种主流框架,基于 mask 和多边形的。但是成本问题够呛。
最近基于 box 的火起来了:BoxSup、Box2Seg、BBTP、BoxInst、BoxLevelSet。但是并没有基于多边形的弱监督实例分割。于是本文就这样出现了。
本文提出一种端到端的 BoxSnake 网络,主要依赖于 CIoU 的一元损失来构建多边形的 bounding box 和距离感知成对损失来最大化标注 box 的 IoU。
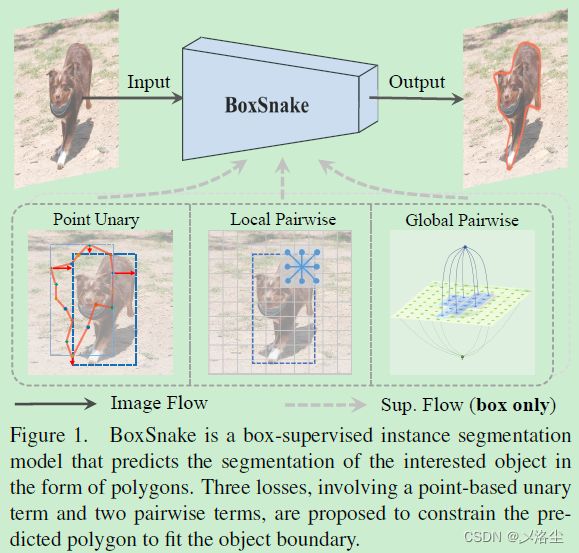
由于一元损失仅能优化预测的多边形最外侧的顶点,因此只能粗糙地回归到目标上而很难拟合边界。于是引入一个基于距离变换的局部和全局成对损失。如下图所示:
其中局部成对损失使得预测的矩形不会变成平直的区域,但相较于 mask 的方法,很难直接优化多边形顶点的坐标,因此尝试将坐标回归问题转化为分类问题。于是从曲线进化中引入一个难映射函数,将 2D 多边形转化为 3D 水平。如下图所示:
将多边形内部和外部的像素映射到两个单独的水平集上。使用距离变换将像素转化到多边形上。采用局部成对损失促进局部窗口内邻居像素的一致性,确保 3D 水平上的两个颜色相似的相邻像素出现在在同一水平级上;采用全局成对损失来最小化相同水平集上像素颜色的变化。
本文提出的方法即插即用,在 COCO 和 Cityscapes 数据集上效果很好。
三、相关工作
基于 Mask 的实例分割
Mask R-CNN、基于 query 的方法。总之,通过一个空间上的密度函数对每个实例的像素进行逐像素分类与二值化。
基于多边形的实例分割
Polygon RNN、Deep Snake、DANCE、PolyTransform、Curve GCN、BoundaryFormer、PolarMask、E2EC。缺点在于标注成本高。
基于 Box 的弱监督实例分割
BBTP、BoxInst、DiscoBox、BoxLevelSet。本文提出一种基于多边形的弱监督实例分割方法。
四、BoxSnake
4.1 定义
图像 I ∈ R H × W × W × 3 \mathcal{I}\in R^{H\times W\times W\times3} I∈RH×W×W×3, N N N 个目标,图像内的像素集 Ω \Omega Ω,每个多边形包含 K K K 个有序的顶点,根据初始角度按逆时针排序。每个目标轮廓上的邻接顶点连线都是一小段分割部分。对于第 n n n 个目标,预测的多边形表示为 C n = { ( x i n , y i n ) } i = 1 K \mathcal{C}^n=\{(x_i^n,y_i^n)\}_{i=1}^K Cn={(xin,yin)}i=1K,对应的 bounding box 为 b n b^n bn,简单表示为 b b b,忽略下标 n n n。
4.2 基于点的一元损失
点的一元损失旨在确保所有预测的多边形顶点都接近 GT box。给定预测的多边形 C \mathcal{C} C 和 GT bounding box (bbox) b b b,于是预测的 bbox 为:
( x 1 , y 1 ) = min ( C ) , ( x 2 , y 2 ) = max ( C ) (x_1,y_1)=\min(\mathcal{C}),\quad(x_2,y_2)=\max(\mathcal{C}) (x1,y1)=min(C),(x2,y2)=max(C)
其中 ( x 1 , y 1 ) (x_1,y_1) (x1,y1) 和 ( x 2 , y 2 ) (x_2,y_2) (x2,y2) 为 bbox b c b_c bc 的左上角点和右下角点。通过最小化基于点的一元损失来降低 b c b_c bc 和 b b b 之间的差异:
L u = 1 − C I o U ( b c , b ) \mathcal{L}_u=1-CIoU(b_c,b) Lu=1−CIoU(bc,b)其中 C I o U ( ⋅ , ⋅ ) CIoU(\cdot,\cdot) CIoU(⋅,⋅) 表示 IoU 的计算。
4.3 距离感知的成对损失

只有一元损失监督的情况下,并不能很好地拟合边界,于是提出一种距离感知的损失,包含局部和全局的成对损失。
局部成对
依据图像上的局部颜色变化,能够定位到目标边界。依据这一假设,提出基于窗口的局部成对损失,来促进预测的多边形和图像边缘的位置保持局部一致。然而这一点很难优化,于是将坐标回归问题转化为分类问题。

如上图所示,引入曲线进化方法将预测的的多边形转化为 3D 水平,从而将多边形内外像素映射到两个分开的水平集上。具体来说,考虑 2D 图像上 ( x , y ) (x,y) (x,y) 位置处的像素,将曲线进化过程定义为一个分离函数 U C ( x , y ) ∈ { 0 , 1 } \mathcal{U}_C(x,y)\in\{0,1\} UC(x,y)∈{0,1},当像素在多边形内时, U C ( x , y ) = 1 \mathcal{U}_C(x,y)=1 UC(x,y)=1,反之 U C ( x , y ) = 0 \mathcal{U}_C(x,y)=0 UC(x,y)=0。这一曲线进化算法能够通过 point-in-polygon (PIP) 算法部署。于是通过最小化局部成对能量函数来定位同一水平集上,相似颜色的像素点: E = ∑ ( p , q ) ∈ Ω ∘ k ( i , j ) w [ ( i , j ) , ( p , q ) ] ∣ U C ( i , j ) − U C ( p , q ) ∣ E=\sum_{(p, q) \in \overset{\circ}\Omega_{k}(i, j)} w_{[(i, j),(p, q)]}\left|\mathcal{U}_{\mathcal{C}}(i, j)-\mathcal{U}_{\mathcal{C}}(p, q)\right| E=(p,q)∈Ω∘k(i,j)∑w[(i,j),(p,q)]∣UC(i,j)−UC(p,q)∣其中 Ω ∘ k ( i , j ) \overset{\circ}{\Omega}_k(i,j) Ω∘k(i,j) 表示 k × k k\times k k×k 窗口位置 ( i , j ) (i,j) (i,j) 处的邻接像素。 W [ ( i , j ) , ( p , q ) ] W[(i,j),(p,q)] W[(i,j),(p,q)] 为两个像素颜色距离的相似程度:
w [ ( i , j ) , ( p , q ) ] = e x p ( − ∥ I ( i , j ) − I ( p , q ) ∥ 2 2 σ I 2 ) w_{[(i,j),(p,q)]}=exp\left(-\dfrac{\|I(i,j)-I(p,q)\|_2}{2\sigma_I^2}\right) w[(i,j),(p,q)]=exp(−2σI2∥I(i,j)−I(p,q)∥2)其中 I ( ⋅ , ⋅ ) I(\cdot,\cdot) I(⋅,⋅) 表述输入坐标的颜色值, ∣ ∣ ⋅ ∣ ∣ 2 ||\cdot||_2 ∣∣⋅∣∣2 表示欧几里德几何距离。 σ I \sigma_I σI 为温度超参数。在边缘上的点使得上式倾向于 0 0 0。若两个邻接像素有着很高的颜色相似度但却赋值给不同的水平集,那么 E E E 式会给予一个高惩罚,反之亦然。
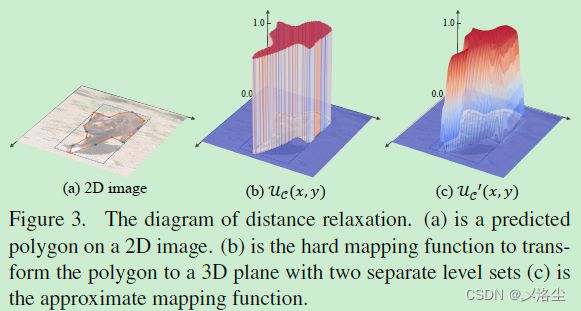
然而 U C ( ⋅ , ⋅ ) \mathcal{U}_C(\cdot,\cdot) UC(⋅,⋅) 是离散的且不可微分,于是引入一个距离变换将这一函数缩放到连续且微分。具体来说,计算像素点 ( x , y ) (x,y) (x,y) 到预测的多边形距离 D c ( x , y ) D_c(x,y) Dc(x,y),并利用 Sigmoid 函数归一化到 ( 0 , 1 ) (0,1) (0,1),于是近似映射函数:
U C ′ ( x , y ) = σ ( 2 ⋅ ( U C ( x , y ) − 0.5 ) ⋅ D C ( x , y ) τ ) \mathcal{U}'_C(x,y)=\sigma\left(\dfrac{2\cdot(\mathcal{U}_C(x,y)-0.5)\cdot D_C(x,y)}{\tau}\right) UC′(x,y)=σ(τ2⋅(UC(x,y)−0.5)⋅DC(x,y))其中 τ \tau τ 为 Sigmoid 操作 σ ( ⋅ ) \sigma(\cdot) σ(⋅) 的温度超参数。如图 3{c}所示,这一近似映射函数在多边形边界上连续且可微。于是提出局部成对损失:
L l p = ∑ ( p , q ) ∈ Ω ∘ k ( i , j ) w [ ( i , j ) , ( p , q ) ] ∣ U C ′ ( i , j ) − U C ′ ( p , q ) ∣ \mathcal{L}_{lp}=\sum_{(p,q)\in \overset{\circ}\Omega_{k}(i,j)}w_{[(i,j),(p,q)]}|\mathcal{U}_C'(i,j)-\mathcal{U}'_C(p,q)| Llp=(p,q)∈Ω∘k(i,j)∑w[(i,j),(p,q)]∣UC′(i,j)−UC′(p,q)∣旨在促进局部区域内相似颜色的像素点能够定位到同一水平集,并且对于目标边界有着一致的距离。咋一看,局部成对损失可能有两个解:预测的多边形拓展到整个图像或塌缩至一个点,但由于基于点的一元损失使得这两种情况都能避免:既能确保多边形在 GT box 内部,又能确保多边形的 bbox 区域和目标标注的 box 匹配上,从而避免拓展到整个图像以及塌缩至单个点。
全局成对
局部区域内的像素变化可能包含噪声而导致不稳定的分割边界,因此提出全局成对损失来减少局部噪声的影响。基于假设:目标内部或外部的区域应该是接近同构的,于是构建全局成对损失如下:
L g p = ∑ ( x , y ) ∈ Ω ∣ ∣ I ( x , y ) − u i n ∣ ∣ 2 ⋅ U C ′ ( x , y ) + ∑ ( x , y ) ∈ Ω ∣ ∣ I ( x , y ) − u o u t ∣ ∣ 2 ⋅ ( 1 − U C ′ ( x , y ) ) \mathcal{L}_{gp}=\sum_{(x,y)\in\Omega}||I(x,y)-u_{in}||_{2}\cdot\mathcal{U}_{\mathcal{C}}'(x,y)+\sum_{(x,y)}\in\Omega||I(x,y)- u_{out}||_{2}\cdot(1-\mathcal{U}'_{\mathcal{C}}(x,y)) Lgp=(x,y)∈Ω∑∣∣I(x,y)−uin∣∣2⋅UC′(x,y)+(x,y)∑∈Ω∣∣I(x,y)−uout∣∣2⋅(1−UC′(x,y))其中 u i n u_{in} uin 和 u o u t u_{out} uout 分别定义为:
u i n = ∑ ( x , y ) ∈ Ω I ( x , y ) ⋅ U C ′ ( x , y ) ∑ ( x , y ) ∈ Ω U C ′ ( x , y ) u_{in}=\dfrac{\sum_{(x,y)\in\Omega}\mathcal{I}(x,y)\cdot\mathcal{U}_C'(x,y)}{\sum_{(x,y)}\in\Omega\mathcal{U}'_C(x,y)} uin=∑(x,y)∈ΩUC′(x,y)∑(x,y)∈ΩI(x,y)⋅UC′(x,y)
u out = ∑ ( x , y ) ∈ Ω I ( x , y ) ⋅ ( 1 − U C ′ ( x , y ) ) ∑ ( x , y ) ∈ Ω ( 1 − U C ′ ( x , y ) ) u_{\text {out }}=\frac{\sum_{(x, y) \in \Omega} \mathcal{I}(x, y) \cdot\left(1-\mathcal{U}_{\mathcal{C}}^{\prime}(x, y)\right)}{\sum_{(x, y) \in \Omega}\left(1-\mathcal{U}_{\mathcal{C}}^{\prime}(x, y)\right)} uout =∑(x,y)∈Ω(1−UC′(x,y))∑(x,y)∈ΩI(x,y)⋅(1−UC′(x,y))而这能够通过近似映射函数来调控。图 2{c} 和图 5{d} 表明全局成对损失能够使得预测的多边形更加光滑及更好地拟合目标轮廓。
裁剪策略
L l p \mathcal{L}_{lp} Llp 和 L g p \mathcal{L}_{gp} Lgp 需要包含背景信息,然而在所有的背景像素上直接计算这些损失可能落地不了,因为需要大量的内存。于是采用双线性插值调整预测的多边形使得 bbox 的尺寸变成 S × S S\times S S×S。接下来根据 GT box 的尺寸,应用 RoIAlign 操作裁剪、调整图像尺寸到 S × S S\times S S×S。相应的,使用裁剪后的图像来引导成对损失。这一策略能够减少内存的消耗。
整体损失如下:
L p o l y g o n = α L u + β L l p + γ L g p \mathcal L_{polygon}=\alpha\mathcal L_u+\beta\mathcal L_{lp}+\gamma\mathcal L_{gp} Lpolygon=αLu+βLlp+γLgp其中 α \alpha α、 β \beta β、 γ \gamma γ 分别为每个损失的控制参数, L u \mathcal L_u Lu 确保多边形紧贴 GT box, L l p \mathcal L_{lp} Llp 和 L u \mathcal L_u Lu 确保预测的多边形更接近目标边界。
4.4 网络结构
将本文提出的方法应用到 Mask R-CNN 上,并采用 Transformer 作为多边形头,Backbone + FPN 提取多尺度特征。如下图所示:

box 回归和分类头产生 bbox 和相应的类别。初始的多边形顶点从接近于 bbox 的椭圆形中采样,然后通过 Transformer 解码器逐步精炼并生成最终的预测多边形。
五、实验
数据集:COCO、Cityscapes。
5.1 实施细节
Mask R-CNN/ResNet/Swin Transformer + FPN + 4 层 Transformer 解码器,64 个轮廓顶点,设置 α = 1.0 \alpha=1.0 α=1.0、 β = 0.5 \beta=0.5 β=0.5、 γ = 0.03 \gamma=0.03 γ=0.03,裁剪尺寸 S × S = 70 × 72 S\times S=70\times72 S×S=70×72,包含 64 × 64 64\times64 64×64 的网格及每边 4 4 4 个零填充,温度设为 0.1 0.1 0.1,窗口尺寸 3 × 3 3\times3 3×3,膨胀系数 2 2 2, σ I = 1.0 \sigma_I=1.0 σI=1.0,bbox 的分类和回归损失与 Mark R-CNN 一致。Backbone 权重初始化在预训练的 ImageNet 上。AdamW 优化器,训练 COCO 90K (1x) 和 180K (2x) 迭代,batch 16,8 GPUs(有钱),初始学习率 1 × 1 0 − 4 1\times10^{-4} 1×10−4,权重衰减 0.1 0.1 0.1。对于 90K 的计划,在 60K 和 80K 上 × 0.1 \times0.1 ×0.1, 180K 的计划,在 120K 和 160K 上 × 0.1 \times0.1 ×0.1。
数据增强:随机翻转、抖动。对于 ResNet 和 Swin Transformer,最短边从 [ 640 , 800 ] [640,800] [640,800] 和 [ 480 , 800 ] [480,800] [480,800] 内随机采样。推理阶段,最短边调整到 800 像素。
对于 Cityscapes 数据集,24K 迭代,batch 8,8 GPUs(有钱),初始学习率 1 × 1 0 − 4 1\times10^{-4} 1×10−4,18K 时 × 0.1 \times0.1 ×0.1,最短边从 [ 800 , 1024 ] [800,1024] [800,1024] 内随机采样,而长边保持 2048 2048 2048。在推理阶段,最短边调整到 1024 像素。两个数据集上的评估均采用 COCO 格式的 mask AP。
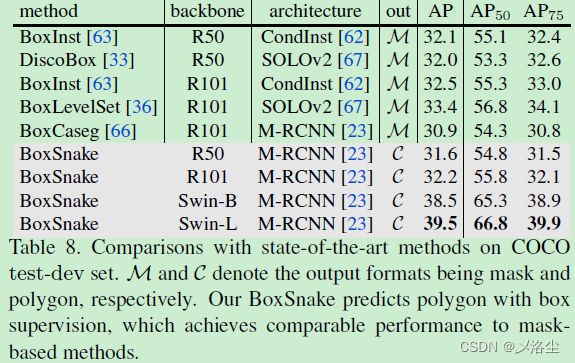
5.2 主要结果
COCO 的结果
Cityscapes 的结果
5.3 消融实验
在 COCO val2017 上进行消融实验,ResNet-50, 1 × 1\times 1× 计划。
不同的一元损失
窗口尺寸的改变
裁剪策略的有效性
不同的初始化方法
每个损失的效果
上表 7。
更大的 Backbone
六、结论
本文引入一种新的端到端,基于多边形的弱监督实例分割方法,主要是整合了一个基于点的一元损失和一个距离感知成对损失,前者最大化 GT box 和预测的多边形 IoU,后者使得预测的多边形更好地拟合目标轮廓且对局部噪声鲁棒。在 COCO 和 Cityscapes 数据集上表现很好。
A、关于距离放缩的细节
D c ( x , y ) D_c(x,y) Dc(x,y) 表示点 ( x , y ) (x,y) (x,y) 到预测的多边形 C = { ( x i , y i ) } i = 1 K \mathcal{C}=\{(x_i,y_i)\}_{i=1}^K C={(xi,yi)}i=1K 的最短距离,令 S 12 = { ( x 1 , y 1 ) , ( x 2 , y 2 ) } S_{12}=\{\left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right)\} S12={(x1,y1),(x2,y2)} 表示从 ( x , y ) (x,y) (x,y) 到 C \mathcal{C} C 的最短分割,于是 D c ( x , y ) D_c(x,y) Dc(x,y) 等于点 ( x , y ) (x,y) (x,y) 到 S 12 S_{12} S12 的距离,记为 D C ( x , y ) = D S 12 ( x , y ) D_\mathcal{C}(x,y) = D_{S_{12}}(x,y) DC(x,y)=DS12(x,y),计算如下:
D S 12 ( x , y ) = { ( x 1 − x ) 2 + ( y 1 − y ) 2 , u < 0 ( x ′ − x ) 2 + ( y ′ − y ) 2 , 0 < u < 1 ( x 2 − x ) 2 + ( y 2 − y ) 2 , u > 1 D_{S_{12}}(x,y)=\begin{cases}\sqrt{(x_1-x)^2+(y_1-y)^2},\quad u<0\\ \sqrt{(x'-x)^2+(y'-y)^2},\quad0
B、附加的消融实验
在 COCO val2017 上对超参数的消融实验。
B.1 成对损失的权重
B.2 距离放缩的温度
C、可视化
写在后面
这篇文章写作可以,创新点也比较新颖,就是这个图啊,安排的确实不咋地,过于混乱,希望写作的同学一定要注意这点。