数据结构与算法----哈夫曼编码练习

步骤

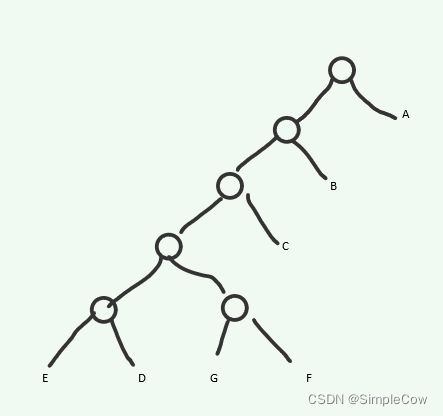
1. 根据给出的数据和权重，构造完整的哈夫曼树
2. 根据哈夫曼树读出对应数据的哈夫曼编码
   1. 读出的过程我选择的是栈，从叶子节点迭代到根节点，出栈的时候字符就是正确的顺序了

具体代码

节点对象

public class HuffmanTreeNode {

    // 双亲节点
    HuffmanTreeNode parentNode;

    // 左孩子节点
    HuffmanTreeNode leftChildNode;

    // 右孩子结点
    HuffmanTreeNode rightChildNode;

    // 双亲节点索引
    Integer parentIndex = 0;

    // 左孩子节点索引
    Integer leftChildIndex = 0;

    // 右孩子节点索引
    Integer rightChildIndex = 0;

    // 值
    Object value;

    // 权重
    Object weight;


    public HuffmanTreeNode getParentNode() {
        return parentNode;
    }

    public void setParentNode(HuffmanTreeNode parentNode) {
        this.parentNode = parentNode;
    }

    public HuffmanTreeNode getLeftChildNode() {
        return leftChildNode;
    }

    public void setLeftChildNode(HuffmanTreeNode leftChildNode) {
        this.leftChildNode = leftChildNode;
    }

    public HuffmanTreeNode getRightChildNode() {
        return rightChildNode;
    }

    public void setRightChildNode(HuffmanTreeNode rightChildNode) {
        this.rightChildNode = rightChildNode;
    }

    public Object getValue() {
        return value;
    }

    public void setValue(Object value) {
        this.value = value;
    }

    public Object getWeight() {
        return weight;
    }

    public void setWeight(Object weight) {
        this.weight = weight;
    }

    public Integer getParentIndex() {
        return parentIndex;
    }

    public void setParentIndex(Integer parentIndex) {
        this.parentIndex = parentIndex;
    }

    public Integer getLeftChildIndex() {
        return leftChildIndex;
    }

    public void setLeftChildIndex(Integer leftChildIndex) {
        this.leftChildIndex = leftChildIndex;
    }

    public Integer getRightChildIndex() {
        return rightChildIndex;
    }

    public void setRightChildIndex(Integer rightChildIndex) {
        this.rightChildIndex = rightChildIndex;
    }

    public HuffmanTreeNode(HuffmanTreeNode parentNode, HuffmanTreeNode leftChildNode, HuffmanTreeNode rightChildNode, Integer parentIndex, Integer leftChildIndex, Integer rightChildIndex, Object value, Object weight) {
        this.parentNode = parentNode;
        this.leftChildNode = leftChildNode;
        this.rightChildNode = rightChildNode;
        this.parentIndex = parentIndex;
        this.leftChildIndex = leftChildIndex;
        this.rightChildIndex = rightChildIndex;
        this.value = value;
        this.weight = weight;
    }

    public HuffmanTreeNode(Object value, Object weight) {
        this.value = value;
        this.weight = weight;
    }

    public HuffmanTreeNode(Integer parentIndex, Integer leftChildIndex, Integer rightChildIndex, Object value, Object weight) {
        this.parentIndex = parentIndex;
        this.leftChildIndex = leftChildIndex;
        this.rightChildIndex = rightChildIndex;
        this.value = value;
        this.weight = weight;
    }

    public HuffmanTreeNode(HuffmanTreeNode parentNode, HuffmanTreeNode leftChildNode, HuffmanTreeNode rightChildNode, Object value, Object weight) {
        this.parentNode = parentNode;
        this.leftChildNode = leftChildNode;
        this.rightChildNode = rightChildNode;
        this.value = value;
        this.weight = weight;
    }

    public HuffmanTreeNode() {
    }

    @Override
    public String toString() {
        return "HuffmanTreeNode{" +
                "parentNode=" + parentNode +
                ", leftChildNode=" + leftChildNode +
                ", rightChildNode=" + rightChildNode +
                ", parentIndex=" + parentIndex +
                ", leftChildIndex=" + leftChildIndex +
                ", rightChildIndex=" + rightChildIndex +
                ", value=" + value +
                ", weight=" + weight +
                '}';
    }
}

具体操作代码

public class HuffmanTreeDemo {

    public static void main(String[] args) {

        // 创建存储数组，大小为2n-1
        List l =new ArrayList(7*2-1);
        l.add(new HuffmanTreeNode("A",new BigDecimal("0.4")));
        l.add(new HuffmanTreeNode("B",new BigDecimal("0.3")));
        l.add(new HuffmanTreeNode("C",new BigDecimal("0.15")));
        l.add(new HuffmanTreeNode("D",new BigDecimal("0.05")));
        l.add(new HuffmanTreeNode("E",new BigDecimal("0.04")));
        l.add(new HuffmanTreeNode("F",new BigDecimal("0.03")));
        l.add(new HuffmanTreeNode("G",new BigDecimal("0.03")));

        // 创建哈夫曼树
        createHuffmanTree(l,7*2-1);

        // 根据哈夫曼树读取哈夫曼编码
        Stack codeStack = new Stack();
        Set> result = new HashSet<>();

        for (int i=0;i map = new HashMap<>();
                map.put(huffmanTreeNode.getValue().toString(), stringBuilder.toString());
                result.add(map);
            }
        }

        // 打印哈弗曼树
        for (int i=0;i< l.size();i++) {
            System.out.println("index:"+i+"|||||||||||"+l.get(i));
        }

        // 打印哈夫曼编码
        Iterator> iterator = result.iterator();
        while(iterator.hasNext()){
            System.out.println(iterator.next());
        }
    }

    private static void stackPush(List l, Stack codeStack, int i, HuffmanTreeNode huffmanTreeNode) {
        // 双亲节点
        HuffmanTreeNode parentNode = l.get(huffmanTreeNode.getParentIndex());

        // 判断当前节点是双亲的哪个孩子结点，左0右1
        if(parentNode.getRightChildIndex() == i) {
            codeStack.push("1");
        }else {
            codeStack.push("0");
        }

        // 如果双亲节点不为0，说明还有双亲节点，需要递归查找
        if(parentNode.getParentIndex() != 0){
            stackPush(l,codeStack,huffmanTreeNode.getParentIndex(),parentNode);
        }
    }

    private static void createHuffmanTree(List l,Integer maxIndex) {
        while (true) {
            // 最小权重的索引
            Integer minIndex = 0;
            // 第二小权重索引
            Integer minIndex1 = 0;

            // 最小权重值
            BigDecimal minValue = BigDecimal.ZERO;
            // 第二小权重值
            BigDecimal minValue1 = BigDecimal.ZERO;

            // 循环查找两个最小的权重的结点
            for (int i = 0; i < l.size(); i++) {
                // 双亲节点不为0的说明已经参加过合并，不再进行操作
                if (l.get(i).getParentIndex() == 0) {
                    // 两个最小的值判断原理，永远将两个中较大的一个拿出作比较
                    if (minValue == BigDecimal.ZERO || minValue.compareTo((BigDecimal) l.get(i).getWeight()) > 0) {
                        // 存储小值
                        minValue = (BigDecimal) l.get(i).getWeight();
                        minIndex1 = minIndex;
                        minIndex = i;

                        // 如果另一个为0或者比第一个大，那么就交换两个的值
                        if(minValue1 == BigDecimal.ZERO || minValue1.compareTo(minValue) >= 0) {
                            BigDecimal temporary = minValue;
                            minValue = minValue1;
                            minValue1 = temporary;
                        }
                    }
                }
            }

            // 创建新的结点
            l.add(new HuffmanTreeNode(0, minIndex, minIndex1, "", minValue.add(minValue1)));
            l.get(minIndex).setParentIndex(l.size() - 1);
            l.get(minIndex1).setParentIndex(l.size() - 1);

            // 如果数组的长度和我们规定的最大值一样，说明结束了
            if (l.size() == maxIndex) {
                break;
            }
        }
    }
}

输出结果

index:0|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=12, leftChildIndex=0, rightChildIndex=0, value=A, weight=0.4}
index:1|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=11, leftChildIndex=0, rightChildIndex=0, value=B, weight=0.3}
index:2|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=10, leftChildIndex=0, rightChildIndex=0, value=C, weight=0.15}
index:3|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=8, leftChildIndex=0, rightChildIndex=0, value=D, weight=0.05}
index:4|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=8, leftChildIndex=0, rightChildIndex=0, value=E, weight=0.04}
index:5|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=7, leftChildIndex=0, rightChildIndex=0, value=F, weight=0.03}
index:6|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=7, leftChildIndex=0, rightChildIndex=0, value=G, weight=0.03}
index:7|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=9, leftChildIndex=6, rightChildIndex=5, value=, weight=0.06}
index:8|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=9, leftChildIndex=4, rightChildIndex=3, value=, weight=0.09}
index:9|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=10, leftChildIndex=8, rightChildIndex=7, value=, weight=0.15}
index:10|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=11, leftChildIndex=9, rightChildIndex=2, value=, weight=0.30}
index:11|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=12, leftChildIndex=10, rightChildIndex=1, value=, weight=0.60}
index:12|||||||||||HuffmanTreeNode{parentNode=null, leftChildNode=null, rightChildNode=null, parentIndex=0, leftChildIndex=11, rightChildIndex=0, value=, weight=1.00}
{A=1}
{C=001}
{G=00010}
{B=01}
{F=00011}
{D=00001}
{E=00000}

结果输出的哈夫曼树样子和王卓老师视频中的样子不太一样，属于是同分异构体的关系。

左0右1即可得出上述结果