李宏毅《机器学习》笔记：3.误差分析和梯度下降
参考文章：
梯度下降：https://www.bilibili.com/video/BV1Tr4y1N7Lh
梯度下降优化：https://www.bilibili.com/video/BV1r64y1s7fU
文章目录
- 1. 误差分析【P5】
-
- 1.1 误差哪里来？
- 1.2 啥是bias 和 variance?
- 1.3 方差，偏差对实验的影响
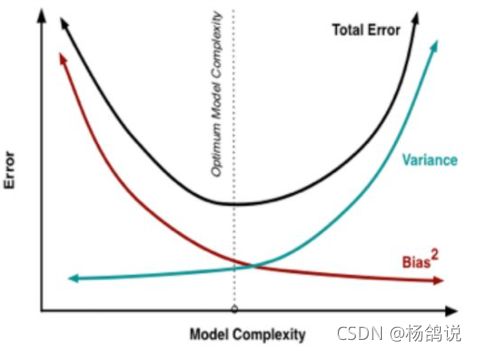
- 1.4 模型选择
- 2. 梯度下降【P6】
-
- 2.1 梯度下降计算过程
-
- 2.1.1 前言回顾
- 2.1.2 正文
- 2.2 如何理解梯度下降
- 3. 梯度下降的优化【P6】
-
- 3.1 优化下降路径
-
- 3.1.1 自适应学习率
- 3.1.2 Adagrad
- 3.2 优化每一步的计算时间
-
- 3.2.1 随机梯度法
- 3.2.2 随机梯度法改进：mini-batch
- 3.2.3 其他方法
- 5.补充：有关误差和梯度下降的计算
-
- 5.5 有关误差分析的数学补充（选读）
-
- 5.5.1 无偏估计
- 5.5.2 偏差计算
- 5.5.3 方差计算
2021.09.05 点赞过1明日更新下一p
LeeML：P5,P6
本系列为原创总结，望点赞支持！！
2021.10.14
去掉了梯度优化牛顿法
对文章进行了优化
第一次录视频，有很多不足的地方，下次改进
李宏毅机器学习笔记：3.误差分析和梯度下降
相关视频：【 梯度下降】【 梯度下降优化】【 我的讲解】
1. 误差分析【P5】
1.1 误差哪里来？
Error 的主要有两个来源，分别是 偏差（bias） 和 方差（variance） 。
1.2 啥是bias 和 variance?
我们打靶，十环打了七环，也就是Error=10-7=3;具体分析，瞄的有问题，瞄的十环，其实是喵的九环，那么bias=10-9=1;枪自己不准，瞄的九没打到九，打着七了，那么variance=9-7=2.
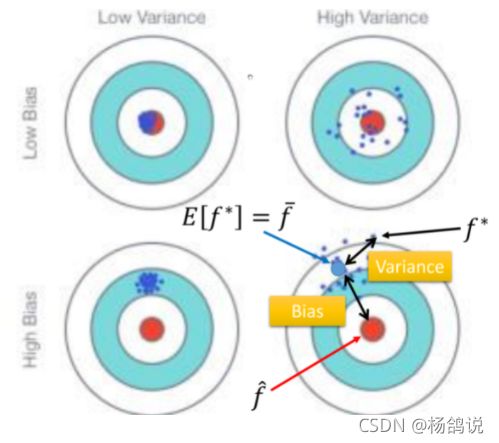
bias 说的是偏差，variance说的是方差，说的是离散的一个程度。
1.3 方差，偏差对实验的影响
-
当你在训练集上追求更低的bias时候，往往这个模型拿到测试集（新数据）上，会有较高的Variance,反而误差不会太小。叫过拟合
类似于第二章笔记说的，我们在训练集上，用更复杂的估值函数式子，可以使得在训练集上误差表现得更好，但拿到测试集上，反而效果不好。
-
在训练集上，我们估函数过于简单，可能会使新数据variance较小，但是太过于简单的式子，并不是我们追求的最优的估值函数，误差往往也能够再缩小。叫做欠拟合
1.4 模型选择
现在在偏差和方差之间就需要一个权衡。
如何权衡？
- Training Set：训练集，就是我们有些数据 训练模型用的
- validation set：验证集，我们通常将训练集的一部分来测试模型好坏。
- Testing Set（绿）：就是训练好的模型，我们用这些数据来看看 模型是不是真的好
- Testing Set(红)：测试集，真正用到的地方，比如自然界
【错误演示】
训练集训练不同的模型，然后在测试集上比较错误率，最小的当成最好的
>> 因为你可能有过拟合现象，不是训练集上训练的越好在测试集就表现的好。
【一种思路】：N-折交叉验证
比如 我们有9k数据，N=3 那么我们三组各3k个数据
- 我们第1次 用1，2两组当训练集，第3组当验证集 来训练三个模型
- 我们第2次 用1，3组当训练集，第2组当验证集 来训练三个模型
- 我们第3次 用2，3组当训练集，第1组当验证集 来训练三个模型
综合表现最好的当选
2. 梯度下降【P6】
2.1 梯度下降计算过程
2.1.1 前言回顾
我们上一章讲了【一个点】梯度下降的计算方法，详看【3.3.3 最佳模型：梯度下降】
例子中，损失函数是 F ( w , b ) = ( w + b ) 2 F(w,b)=(w+b)^2 F(w,b)=(w+b)2
- 这个损失函数是真实值 （ x , y ^ ） = ( 1.0 ) , 估 算 函 数 y = w x + b 来 的 （x,\hat{y}）=(1.0),估算函数y=wx+b来的 （x,y^）=(1.0),估算函数y=wx+b来的
- 当x=1带入损失函数 F ( w , b ) = ( y ^ − y ) 2 F(w,b)=(\hat{y}-y)^2 F(w,b)=(y^−y)2
- 我们通过梯度下降最终得出了w+b=0的时候，损失函数为0
【3.3.3】梯度下降的实力说了个什么事呢？
- 也就是，点（1,0）在满足w+b=0条件下的线性方程式wx+b=0损失函数为0
我们举个例子w=2 b=-2 那么估值方程2x-2=0是不是正好穿过这个点？是的!
- 换句话说 也就是一个点（数据，严谨点二维数据），一定是可以一条线（估值函数）穿过它，是它损失函数为0，也就是真实值和估值一样，这个估值函数就是我们猜测的模型。
2.1.2 正文
那真实的数据是什么样的？对，不止一个数据，万万千千的数据。
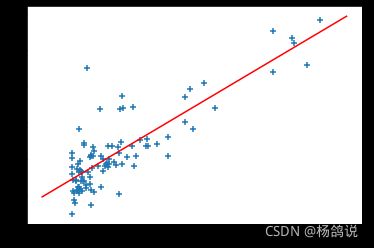
那我们很容易就理解损失函数了，目的就是是所有数据损失函数相加最小的一条分割线。
【完整的计算过程】
① 损失函数
- h ( θ ) h(\theta) h(θ)是多维的
- J ( θ ) J(\theta) J(θ)是所有数据的损失之和，才是我们真正需要的损失函数
② 损失函数 J ( θ ) 对 参 数 θ j J(\theta)对参数\theta_j J(θ)对参数θj的偏导
.
- 更新每个数据的每一个参数 θ \theta θ,重复做，直到参数小于一个临界值
.
a为步长，学习因子
这部结合上章（1.0）点的例子看计算过程，需要更新每一个参数（上章为w,b），直到损失函数导数为0（小于某个很小值）
2.2 如何理解梯度下降
以二维为例，J就是损失函数，我们想让J最小，那跟下山一样
.
- 从一个点看：我环顾四周，最陡的地方，走一个步长，走到新位置再看四周，再选个最陡的地方 再走一个步长…直到走到最低点。
- 从多个点看，你选这个最快的路 别的人走 不一定总代价最小（最快）。所以最快的路是，每条路所有人都这么走一趟，总代价/人数算出的平均代价，最低的，就是我们损失函数减小最快的路径
3. 梯度下降的优化【P6】
我们梯度下降优化总体有两个思路，一个是 优化下降路径，另一个是 减少每走一步的计算量。
3.1 优化下降路径
.
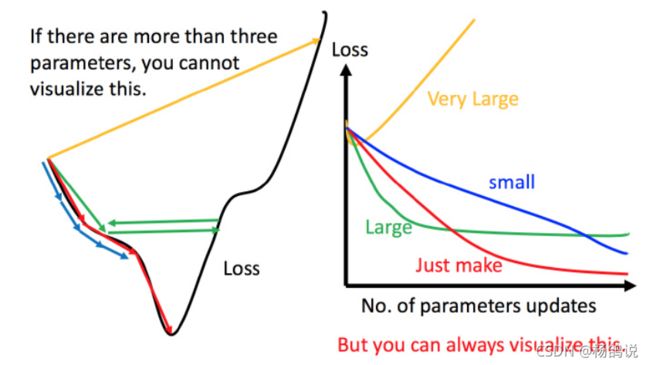
- 如果学习率很小（蓝色），那么一定是可以到最优点，问题是：学习率（步伐）太小，那么步数会增多，下降的慢
- 如果加大学习率，那么一步可以迈较大（绿色），在最优解附近会产生振荡
- 如果学习率非常大（黄色），可能就错过了最优解，得出的损失值始终很大
3.1.1 自适应学习率
【想法】 开始步伐大点，走快点；然后越接近终点，步伐越小。那么很自然想到，学习率加入次数或者是时间参数
3.1.2 Adagrad
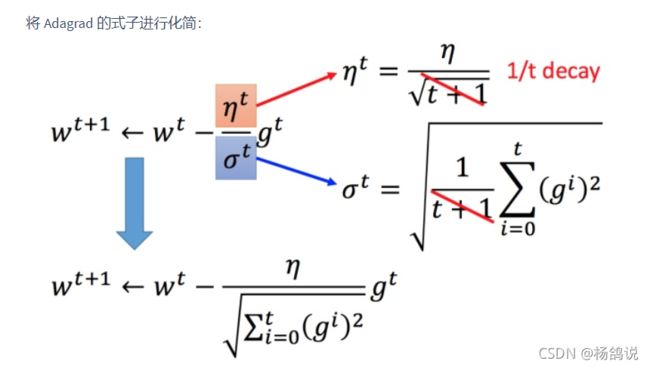
【① 观察规律】
- 按照 【老猫】说法，二次导数比较难求，Adagrad算法其实是估算的（图中问号代表的就是估算的意思）
【② 整体公式】
【③ 可行的原因】
杨鸽理解：Adagrad不仅考虑到了开始步可以放大一点，后面步伐小一点的问题；还做了一个改进：就是我们在梯度比较大的时候，那么要下降的比较小心；梯度比较小 比较平缓的时候，你步伐相应可以大一点快速走过平摊路段。这就是要除以梯度累加和开更号【不知道理解是否正确？】
3.2 优化每一步的计算时间
比如我们有10000个数据，每个数据10个参数，【传统梯度下降】那么我们每走一步 要计算10万次。通常数据量很大，传统方法通常很难完成这样的时间代价
3.2.1 随机梯度法
stochastic gradient descent，SGD
【思路】当调查中国男人平均身高时候，我们不需要把每个人都量了求平均，只需要抽样求平均就行
【方法】我们每走一步时候，不算1万个数据，只是从中随机选一个数据，选最陡的山路的方向迈一步；下一步，还是随机选一个数据，在第一步结束的位置，往第二次随机出来样本的最陡方向再迈一步，这样一步一步，直到走到最低处。
上个例子，每一步只需要随意出来一个数据，计算10个参数的十次计算就行
3.2.2 随机梯度法改进：mini-batch
一个数据可能会错过最优解，所以我们随机一小批数据 来计算，就比一个准确。
我们现在一般说的随机梯度，其实默认的就是这种办法
上个例子，我每一步 随出来50个 ，那么既能保证比1个数据精准，又能节省大量计算时间，每步计算500次
3.2.3 其他方法
李宏毅《机器学习》笔记：9. 神经网络改进流程：https://blog.csdn.net/wistonty11/article/details/120572130
.
5.补充：有关误差和梯度下降的计算
5.5 有关误差分析的数学补充（选读）
- 假设x的平均值是 μ，方差为 σ 2 ^2 2
5.5.1 无偏估计
- 我们从非常多的样本中取出N个样本点：{ x 1 , x 2 . . . . x n {x^1,x^2....x^n} x1,x2....xn}
- 这N个点的平均值 m = 1 N ∑ n = N 1 x n ≠ m=\frac{1}{N}\sum^1_{n=N}{x^n}\not= m=N1∑n=N1xn= μ
μ为整个样本的平均值，而m为从中去N个样本的期望（平均值），通常是不相等的
但如果许多组M,M非常非常大，那么两者是相等的，这个估计叫做无偏估计（unbiased）
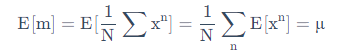
5.5.2 偏差计算
其实说的一件事：样本均值抽样分布的方差等于总体方差的n分之一
