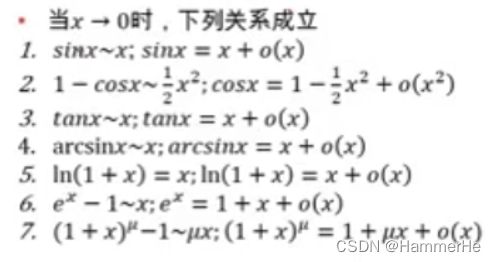1221学习笔记

数学基础篇（函数极限与连续函数）

1.函数极限

1.1 函数极限的定义

在自变量的某个变化过程中，如果对应的函数值无限接近于某个确定的数，那么这个确定的数就叫做在一变化过程中的函数的极限

1.2 单侧极限

右极限的定义：
其中用数轴的方式去表示，就是当x处于（a,a+q）的区间时，f(x)会处在（-,+）这个带型区域内。

反之左极限的定义是：
当就是当x处于（a-q，a）的区间时，f(x)会处在（-,+）这个带型区域内,只是关于x的取值有一定改变。

1.3 双侧极限

注意：
（1）极限是否存在和极限的值 和f(a)的值没有任何关系，简单的例子 函数在a点断掉的清空。
（2）双侧极限存在等价于左右极限存在且相等
（3）极限值唯一性

1.4 极限的性质

（1）函数极限和四则运算可以交换顺序，先加后算极限和先算极限后加是一样的

（2）函数的极限可以通过复合方式去得到：
如:

(3)保号性（类似于数列的保序性）：
（4）夹逼定理（和数列一样）：

1.6 自变量趋向无穷的时候的极限（极限计算）

广义极限：极限趋向正无穷。

1.7函数中的重要极限

（1）极限为e
当这个函数趋向于负无穷的时候极限也是e

(2)

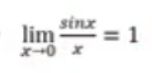
由无穷小量阶来决定这个极限，即sinx和x的无穷小量等价
几何方法加夹逼定理证明

1.8 函数的无穷小量

1.9 常见等价无穷小的关系

2 连续函数

2.1 函数的连续性和极限的关系

2.2连续函数的性质

（1）四则运算会保持函数的连续性，即两个连续函数相加得到的函数还是连续的
（2）函数的复合也会保持连续性
（3）反函数的连续性：必须一一映射且严格单调的连续函数的反函数会保持连续性。
（4）初等函数的连续性：每个初等函数在其定义域内任何一个区间都是连续的
（5）介值定理：
简单的说：介值定理说明对于某区间上的连续函数，给定两个值后，可以取得两个值中间的所有值
定义：
注意：在开区间介值定理不成立

（6）最值定理：
简单的说：在闭区间内一定存在函数最大值和最小值，单开区间不成立
定义：

（7）有界性定理：
闭区间上的连续函数一定有界（和最值定理意义差不多）
定义：

2.3 间断点的定义

2.4 连续性定理的实用意义

（1）证明：（所有奇数次方多项式一定有实根）实系数多项式：系数为实数的多项式

Python数据结构篇（链表）

1.1 链表的定义

本质上是用了两大块地址代表一个链表节点，每个节点存储当前值和下个节点的起始地址

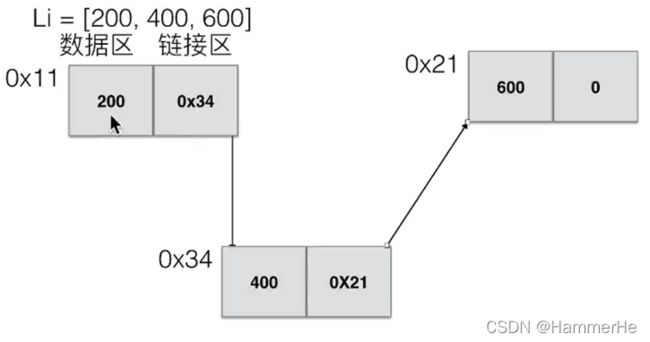
1.2 单向链表

单向链表的每个节点包含两个域，一个信息域（元素域）和一个链接域。

链接域的这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。
同时
第一个节点叫头节点
最后一个节点叫尾节点

基础结构如下

1.4 拓展知识（Python变量标识的本质）

（1）变量赋值绷直

数值1在内存中有个地址

a=1：a是一个指针，指针就是存储一个内存地址的变量
a--------->指向1在内存中的地址

a=2：1在内存中的地址没有发生改变
本质：a这个指针指向了内存2存在的地址

（2）变量的本质
存储在内存中变量的地址变了（值的地址没有被改变）

（3）变量交换的本质
a,b=b,a
存储在a,b的地址被互换了

（4）在Python里面函数也是一个对象，a也可以等于一个函数

（5）由于变量的本质，所以在Python里面不需要对变量进行定义，变量可以是任何数据类型。

以上的东西证明了一点：node1.next=node2是成立的，相当于next是个变量指向下一个节点。

1.3 在Python里面实现单链表

链表节点的实现

class SingleNode(object):
    """单链表的结点"""
    def __init__(self,item):#这是构造函数
        # _item存放数据元素
        self.item = item
        # _next是下一个节点的标识
        self.next = None

单链表的实现和相关操作的实现
1.注意：遍历结束的条件有两种curNone或者cur.nextNone,一个表示当前节点是最后一个节点的指向节点，后一个cur表示当前节点，在操作里会在不同时候用到这两个遍历结束条件
2.插入一个node的操作是：

node.next = pre.next 
pre.next = node

3.删除一个节点（cur）的操作

cur=pre.next 
pre.next = cur.next

其中pre是前驱节点

最终得到一系列的代码为：

"""首先建立节点的类"""


class SingleNode(object):
    # 首先建立构造函数
    def __init__(self, item):
        # _item存放数据元素
        self.item = item
        # _next是下一个节点的标识
        self.next = None


"""然后建立单链表的类"""


class SingleLinkedList(object):
    # 首先还是构造函数：构造函数需要一个默认参数（没有输入头节点把头节点置空，输入头节点头节点置输入值）
    def __init__(self, node=None):
        self._head = node

    # 判断链表是否为空
    def is_empty(self):
        return self._head is None

    # 判断链表的长度
    def length(self):
        cur = self._head
        count = 0
        while cur is not None:
            cur = cur.next
            count += 1
        return count

    # 遍历链表并打印
    def travel(self):
        cur = self._head
        while cur is not None:
            print(cur.item, end=' ')
            cur = cur.next
        print("")

    # 头部增加元素
    def add(self, item):
        node = SingleNode(item)
        node.next = self._head
        self._head = node

    # 尾部增加元素
    def append(self, item):
        node = SingleNode(item)
        # 先判断是不是空链表
        if self.is_empty():
            self._head = node
        # 不是空链表，先遍历到尾部
        cur = self._head
        while cur.next is not None:
            cur = cur.next
        cur.next = node

    # 指定位置增加节点
    def insert(self, index, item):
        # 插入节点在头部，直接插入
        if index <= 0:
            self.add(item)
        # 插入值在尾部，即index大于最后一个下标，即len-1
        elif index >= (self.length() - 1):
            self.append(item)
        else:
            node = SingleNode(item)
            pre = self._head
            # # 先遍历index次,找到pre为插入位置的前一项
            # for i in range(0, index - 1):
            #     pre = pre.next
            count = 0
            while count < (index - 1):
                count += 1
                pre = pre.next

            # 先将新节点node的next指向插入位置的节点
            node.next = pre.next
            # 将插入位置的前一个节点的next指向新节点
            pre.next = node

    # 查找某个节点,返回真假(相同元素的情况下返回前面的)
    def search(self, item):
        cur = self._head
        while cur is not None:
            if cur.item == item:
                return True
            else:
                cur = cur.next
        return False

    # 删除某个元素节点
    def remove(self, item):
        cur = self._head
        pre = None
        while cur is not None:
            if cur.item == item:
                # 根据pre是不是为空来，判断当前cur是不是头节点
                if not pre:
                    self._head = cur.next
                else:
                    pre.next = cur.next
                break
            else:
                pre = cur
                cur = cur.next


if __name__ == "__main__":
    ll = SingleLinkedList()
    ll.add(1)
    ll.add(2)
    ll.append(3)
    ll.insert(8, 5)
    print("length:", ll.length())
    ll.travel()
    print(ll.search(3))
    print(ll.search(5))
    ll.remove(4)
    print("length:", ll.length())
    ll.travel()

1.4 链表与顺序表的对比

通过一个不同操作时间复杂度的对比可以看出：
可以看到链表的主要耗时操作是遍历查找，删除和插入操作本身的复杂度是O(1)。顺序表查找很快，主要耗时的操作是拷贝覆盖。
因为除了目标元素在尾部的特殊情况，顺序表进行插入和删除时需要对操作点之后的所有元素进行前后移位操作，只能通过拷贝和覆盖的方法进行。

另外：
链表失去了顺序表随机读取的优点，同时链表由于增加了结点的指针域，增加了空间开销
链表对于对存储空间的使用要相对灵活。