干货 ：手把手教你用Python进行时间序列分解和预测

作者：Mohit Sharma   翻译：王闯（Chuck)   校对：王可汗

本文约4100字，建议阅读10+分钟

本文介绍了用Python进行时间序列分解的不同方法，以及如何在Python中进行时间序列预测的一些基本方法和示例。 

预测是一件复杂的事情，在这方面做得好的企业会在同行业中出类拔萃。时间序列预测的需求不仅存在于各类业务场景当中，而且通常需要对未来几年甚至几分钟之后的时间序列进行预测。如果你正要着手进行时间序列预测，那么本文将带你快速掌握一些必不可少的概念。

目录

• 什么是时间序列？

• 如何在Python中绘制时间序列数据？

• 时间序列的要素是什么？

• 如何分解时间序列？

• 经典分解法

• 如何获得季节性调整值？

• STL分解法

• 时间序列预测的基本方法：

• Python中的简单移动平均（SMA）

• 为什么使用简单移动平均？

• Python中的加权移动平均（WMA）

• Python中的指数移动平均（EMA）

什么是时间序列？

顾名思义，时间序列是按照固定时间间隔记录的数据集。换句话说，以时间为索引的一组数据是一个时间序列。请注意，此处的固定时间间隔（例如每小时，每天，每周，每月，每季度）是至关重要的，意味着时间单位不应改变。别把它与序列中的缺失值混为一谈。我们有相应的方法来填充时间序列中的缺失值。

在开始使用时间序列数据预测未来值之前，思考一下我们需要提前多久给出预测是尤其重要的。你是否应该提前一天，一周，六个月或十年来预测（我们用“界限”来表述这个技术术语）？需要进行预测的频率是什么？在开始预测未来值的详细工作之前，与将要使用你的预测结果的人谈一谈也不失为一个好主意。

如何在PYTHON中绘制时间序列数据？

可视化时间序列数据是数据科学家了解数据模式，时变性，异常值，离群值以及查看不同变量之间的关系所要做的第一件事。从绘图查看中获得的分析和见解不仅将有助于建立更好的预测，而且还将引导我们找到最合适的建模方法。这里我们将首先绘制折线图。折线图也许是时间序列数据可视化最通用的工具。

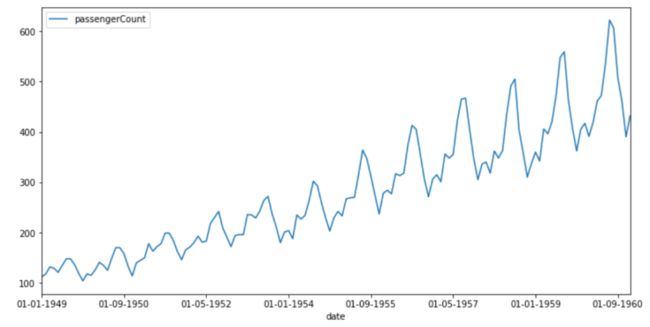
这里我们用到的是AirPassengers数据集。该数据集是从1949年到1960年之间的每月航空旅客人数的集合。下面是一个示例数据，以便你对数据信息有个大概了解。

#Reading Time Series Data
Airpassenger = pd.read_csv("AirPassengers.csv")
Airpassenger.head(3)

现在，我们使用折线图绘制数据。在下面的示例中，我们使用set_index（）将date列转换为索引。这样就会自动在x轴上显示时间。接下来，我们使用rcParams设置图形大小，最后使用plot（）函数绘制图表。

Airpassenger = Airpassenger.set_index('date')
pyplot.rcParams["figure.figsize"] = (12,6)
Airpassenger.plot()
pyplot.show()

航空旅客人数

 

1949-1960年间，乘飞机旅行的乘客人数稳定增长。规律性间隔的峰值表明增长似乎在有规律的时间间隔内重复。

让我们看看每个季度的趋势是怎样的。为了便于理解，从不同的维度观察信息是个好主意。为此，我们需要使用Python中的datetime包从date变量中得出季度和年份。在进行绘图之前，我们将连接年份和季度信息，以了解旅客数量在季节维度上如何变化。

from datetime import datetime
# Airpassenger["date"] = Airpassenger["date"].apply(lambda x: datetime.strptime(x, "%d-%m-%Y"))
Airpassenger["year"] = Airpassenger["date"].apply(lambda x: x.year)
Airpassenger["qtr"] = Airpassenger["date"].apply(lambda x: x.quarter)
Airpassenger["yearQtr"]=Airpassenger['year'].astype(str)+'_'+Airpassenger['qtr'].astype(str)
airPassengerByQtr=Airpassenger[["passengerCount", "yearQtr"]].groupby(["yearQtr"]).sum()

准备好绘制数据后，我们绘制折线图，并确保将所有时间标签都放到x轴。x轴的标签数量非常多，因此我们决定将标签旋转呈现。

pyplot.rcParams["figure.figsize"] = (14,6)
pyplot.plot(airPassengerByQtr)
pyplot.xticks(airPassengerByQtr.index, rotation='vertical')

每季度的旅客总数

这幅图非常有趣，它清晰地表明，在1949-1960年之间的所有年份中，航空旅客人数每季度都在显著增加。

时间序列的要素是什么？

时间序列数据包含4个主要元素：

1. 趋势性–趋势性表示数据随时间增加或减少的一般趋势。这很容易理解。例如，1949年至1960年之间航空旅客数量呈增加趋势，或者可以说呈上升趋势。

2. 季节性–如同一年四季，数据模式出现在有规律的间隔之后，代表了时间序列的季节性组成部分。它们在特定的时间间隔（例如日，周，月，年等）之后重复。有时我们很容易弄清楚季节性，有时则未必。通常，我们可以绘制图表并直观检验季节性元素的存在。但是有时，我们可能不得不依靠统计方法来检验季节性。

3. 周期性–可被视为类似季节性，但唯一的区别是周期性不会定期出现。这个属性使得它很难被辨识。例如，地震可以在我们知道将要发生的任何时间发生，但是我们其实不知道何时何地发生。

4. 随机噪声–不属于上述三类情况的时间序列数据中的突然变化，而且也很难被解释，因此被称为随机波动或随机噪声。

如何分解时间序列？

有两种技术可以获取时间序列要素。在进行深入研究和查看相关Python抽取函数之前，必须了解以下两点：

• 时间序列不必具有所有要素。

• 弄清该时间序列是可加的还是可乘的。

那么什么是可加和可乘时间序列模型呢？

可加性模型–在可加性模型中，要素之间是累加的关系。

y（t）=季节+趋势+周期+噪音

 

可乘性模型–在可乘性模型中，要素之间是相乘的关系。

y（t）=季节*趋势*周期*噪音

你想知道为什么我们还要分解时间序列吗？你看，分解背后的目的之一是估计季节性影响并提供经过季节性调整的值。去除季节性的值就可以轻松查看趋势。例如，在美国，由于农业领域需求的增加，夏季的失业率有所下降。从经济学角度来讲，这也意味着6月份的失业率与5月份相比有所下降。现在，如果你已经知道了逻辑，这并不代表真实的情况，我们必须调整这一事实，即6月份的失业率始终低于5月份。

这里的挑战在于，在现实世界中，时间序列可能是可加性和可乘性的组合。这意味着我们可能并不总是能够将时间序列完全分解为可加的或可乘的。

现在你已经了解了不同的模型，下面让我们研究一些提取时间序列要素的常用方法。

经典分解法

该方法起源于1920年，是诸多方法的鼻祖。经典分解法有两种形式：加法和乘法。Python中的statsmodels库中的函数season_decompose（）提供了经典分解法的实现。在经典分解法中，需要你指出时间序列是可加的还是可乘的。你可以在此处（https://otexts.com/fpp2/classical-decomposition.html）了解有关加法和乘法分解的更多信息。

在下面的代码中，要获得时间序列的分解，只需赋值model=additive。

import numpy as np
from pandas import read_csv
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from pylab import rcParams


elecequip = read_csv(r"C:/Users/datas/python/data/elecequip.csv")
result = seasonal_decompose(np.array(elecequip), model='multiplicative', freq=4)


rcParams['figure.figsize'] = 10, 5
result.plot()
pyplot.figure(figsize=(40,10))
pyplot.show()

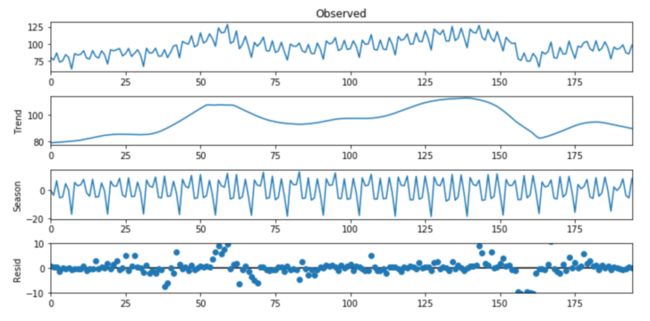
上图的第一行代表实际数据，底部的三行显示了三个要素。这三个要素累加之后即可以获得原始数据。第二个样本集代表趋势性，第三个样本集代表季节性。如果我们考虑完整的时间范围，你会看到趋势一直在变化，并且在波动。对于季节性，很明显，在规律的时间间隔之后可以看到峰值。

如何获得季节性调整值？

对于可加性模型，可以通过y（t）– s（t）获得季节性调整后的值，对于乘法数据，可以使用y（t）/ s（t）来调整值。

如果你正想问为什么我们需要季节性调整后的数据，让我们回顾一下刚才讨论过的有关美国失业率的示例。因此，如果季节性本身不是我们的主要关注点，那么季节性调整后的数据将更有用。尽管经典方法很常见，但由于以下原因，不太建议使用它们：

• 该技术对异常值不可靠。

• 它倾向于使时间序列数据中的突然上升和下降过度平滑。

• 假设季节性因素每年只重复一次。

• 对于前几次和最后几次观察，该方法都不会产生趋势周期估计。

其他可用于分解的更好方法是X11分解，SEAT分解或STL分解。现在，我们将看到如何在Python中生成它们。

与经典法，X11和SEAT分解法相比，STL具有许多优点。接下来，让我们探讨STL分解法。

STL分解法

STL代表使用局部加权回归（Loess）进行季节性和趋势性分解。该方法对异常值具有鲁棒性，可以处理任何类型的季节性。这个特性还使其成为一种通用的分解方法。使用STL时，你控制的几件事是：

• 趋势周期平滑度

• 季节性变化率

• 可以控制对用户异常值或异常值的鲁棒性。这样你就可以控制离群值对季节性和趋势性的影响。

同任何其他方法一样，STL也有其缺点。例如，它不能自动处理日历的变动。而且，它仅提供对可加性模型的分解。但是你可以得到乘法分解。你可以首先获取数据日志，然后通过反向传播要素来获取结果。但是，这超出了本文讨论的范围。

Import pandas as pd
Import seaborn as sns
Import matplotlib.pyplot as plt
From statsmodels.tsa.seasonal import STL


elecequip =read_csv(r"C:/Users/datas/python/data/elecequip.csv")
stl = STL(elecequip, period=12, robust=True)
res_robust = stl.fit()
fig = res_robust.plot()

时间序列预测的基本方法

尽管有许多统计技术可用于预测时间序列数据，我们这里仅介绍可用于有效的时间序列预测的最直接、最简单的方法。这些方法还将用作其他方法的基础。

PYTHON中的简单移动平均（SMA）

简单移动平均是可以用来预测的所有技术中最简单的一种。通过取最后N个值的平均值来计算移动平均值。我们获得的平均值被视为下一个时期的预测。

为什么使用简单移动平均？

移动平均有助于我们快速识别数据趋势。你可以使用移动平均值确定数据是遵循上升趋势还是下降趋势。它可以消除波峰波谷等不规则现象。这种计算移动平均值的方法称为尾随移动平均值。在下面的示例中，我们使用rolling（）函数来获取电气设备销售数据的移动平均线。

Import pandas as pd
from matplotlib import pyplot


elecequip = pd.read_csv(r"C:/Users/datas/python/data/elecequip.csv")


# Taking moving average of last 6 obs
rolling = elecequip.rolling(window=6)
rolling_mean = rolling.mean()


# plot the two series
pyplot.plot(elecequip)
pyplot.plot(rolling_mean, color='red')
pyplot.show()

另一种方法是“中心移动平均”。在这里将任意给定时间（t）的值计算为当前，之前和之后的平均值。启用center = True将提供中心移动平均值。

elecequip["x"].rolling(window=3, center=True).mean()

PYTHON中的加权移动平均（WMA）

简单移动平均非常朴素，因为它对过去的所有值给予同等的权重。但是当假设最新数据与实际值密切相关，则对最新值赋予更多权重可能更有意义。

要计算WMA，我们要做的就是将过去的每个观察值乘以一定的权重。例如，在6周的滚动窗口中，我们可以将6个权重赋给最近值，将1个权重赋给最后一个值。

import random
rand = [random.randint(1, i) for i in range(100,110)]
data = {}
data["Sales"] = rand


df = pd.DataFrame(data)
weights = np.array([0.5, 0.25, 0.10])


sum_weights = np.sum(weights)
df['WMA']=(df['Sales']
.rolling(window=3, center=True)
.apply(lambda x: np.sum(weights*x)/sum_weights, raw=False)


)
print(df['WMA'])

PYTHON中的指数移动平均（EMA）

在“指数移动平均”中，随着观察值的增加，权重将按指数递减。该方法通常是一种出色的平滑技术，可以从数据中消除很多噪声，从而获得更好的预测。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.api import ExponentialSmoothing


EMA_fit = ExponentialSmoothing(elecequip, seasonal_periods=12, trend='add', seasonal='add').fit(use_boxcox=True)
fcast3 = EMA_fit.forecast(12)




ax = elecequip.plot(figsize=(10,6), marker='o', color='black', title="Forecasts from Exponential Smoothing" )
ax.set_ylabel("Electrical Equipment")
ax.set_xlabel("Index")


# For plotting fitted values
# EMA_fit.fittedvalues.plot(ax=ax, style='--', color='red')


EMA_fit.forecast(12).rename('EMS Forecast').plot(ax=ax, style='--',
 marker='o', color='blue', legend=True)

该方法具有以下两种变体： 

1. 简单指数平滑–如果时间序列数据是具有恒定方差且没有季节性的可加性模型，则可以使用简单指数平滑来进行短期预测。

2. Holt指数平滑法–如果时间序列是趋势增加或减少且没有季节性的可加性模型，则可以使用Holt指数平滑法进行短期预测。

以下是从python中的statsmodels包导入两个模型的代码。现在，你可以在练习中运行上述模型。

 

1 2 3 4

import numpy as np import pandas as pd import matplotlib.pyplot as plt from statsmodels.tsa.api import SimpleExpSmoothing, Holt

 

在本长篇教程中，我们讲解了：

• 什么是时间序列数据？

• 如何可视化和更深入地识别数据模式（如果有）？

• 介绍了可加性和可乘性时间序列模型。

• 研究了Python中分解时间序列的不同方法。

• 最后，我们学习了如何在Python中运行一些非常基本的方法，例如移动平均（MA），加权移动平均（WMA），指数平滑模型（ESM）及其变体，例如SESM和Hotl。

原文标题：

TIME SERIES FORECAST AND DECOMPOSITION – 101 GUIDE PYTHON

原文链接：

https://datasciencebeginners.com/2020/11/25/time-series-forecast-and-decomposition-101-guide-python/

译者简介：王闯（Chuck），台湾清华大学资讯工程硕士。曾任奥浦诺管理咨询公司数据分析主管，现任尼尔森市场研究公司数据科学经理。很荣幸有机会通过数据派THU公众号平台和各位老师、同学及同行前辈们交流学习。

END

版权声明：本号内容部分来自互联网，转载请注明原文链接和作者，如有侵权或出处有误请和我们联系。

---

合作请加QQ：365242293  

数据分析（ID : ecshujufenxi ）互联网科技与数据圈自己的微信，也是WeMedia自媒体联盟成员之一，WeMedia联盟覆盖5000万人群。