第七届蓝桥杯省赛C/C++ B组 题解

第七届蓝桥杯省赛C/C++ B组

煤球数目
题意：

按照题目的要求求出第100层，共有多少煤球

思路：

1，3，6，10…d1=2,d2=3,d3=4…dn=n-1,如果需要求第n项累加求和即可。

#include
using namespace std;
int main()
{
    int n;//第n层
while(cin>>n)
{    int sum=0;
    for(int i=1;i<=n;i++)
    {
        sum+=i;
    }cout<<sum<<endl;}}
//5050

生日蜡烛
题意:

一个人从他第n岁开始过生日并且吹灭与他岁数相同数量的蜡烛。问当他多少岁开始过生日时，吹灭的蜡烛数量为236.

思路：

可以转换为一个简单的数学问题
(n+n+k)*(k+1)/2==236， 随后跑两层for循环，写入判断条件，具体看代码。

代码

#include
using namespace std;
int main()
{
//(n+n+k)*(k+1)/2==236
for(int n=1;n<236;n++)
for(int k=1;k<236;k++)
{
if((n+n+k)*(k+1)/2==236)
cout<<n<<" "<<k<<endl;
    }
}//n=26,k=7,说明一共有8项
//26,27,28,29,30,31,32,33

凑算式

题意：

由1-9，9个数字组成a-i，有多少种组合满足图片中的等式

代码一：暴力

#include
using namespace std;
int main()
{ int sum=0;
for(int a=1;a<=9;a++)
{for(int b=1;b<=9;b++){
if(b==a)continue;
for(int c=1;c<=9;c++){
if(c==a||c==b)continue;
for(int d=1;d<=9;d++){
if(d==a||d==b||d==c)continue;
for(int e=1;e<=9;e++){
if(e==a||e==b||e==c||e==d)continue;
for(int f=1;f<=9;f++){
if(f==a||f==b||f==c||f==d||f==e)continue;
for(int g=1;g<=9;g++){
if(g==a||g==b||g==c||g==d||g==e||g==f)continue;
for(int h=1;h<=9;h++){
if(h==a||h==b||h==c||h==d||h==e||h==f||h==g)continue;
for(int i=1;i<=9;i++){
if(i==a||i==b||i==c||i==d||i==e||i==f||i==g||i==h)continue;
if((a*c+b)*(100*g+10*h+i)+(100*d+10*e+f)*c==10*c*(100*g+10*h+i))
{sum++;}}}}}}}}}}
cout<<sum<<endl;}
//答案29

代码二：全排列

#include
using namespace std;
int main()
{
    for(int i=1;i<=9;i++)
        a[i]=i;
    int ant=0;
    do{//将等式通分
        if((a[1]*a[3]+a[2])*(100*a[7]+10*a[8]+a[9])+(100*a[4]+10*a[5]+a[6])*a[3]==10*a[3]*(100*a[7]+10*a[8]+a[9]))
            ant++;
    }while(next_permutation(a+1,a+9+1));
    cout<<ant<<endl;
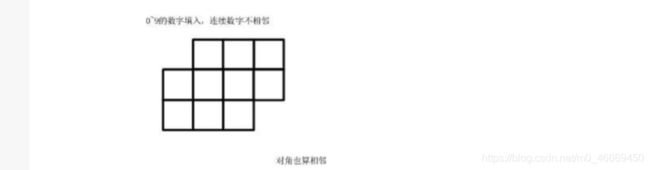
}//答案29

方格填数


题意：

就是将0-9这十个数字按要求填入表格中。问有多少种方法。

思路：

因为填入的数字不多，可以使用全排列，如果需要填入的数字很多，则使用DFS。

代码

#include
using namespace std;
int a[10]={0,1,2,3,4,5,6,7,8,9};
int sum;
void solve(){
sum=0;
 do{//按要求填数
     if(abs(a[1]-a[0])==1||abs(a[2]-a[1])==1||abs(a[3]-a[2])==1||abs(a[4]-a[3])==1||abs(a[5]-a[4])==1||
       abs(a[6]-a[5])==1||abs(a[8]-a[7])==1||abs(a[9]-a[8])==1||abs(a[4]-a[1])==1||abs(a[5]-a[0])==1||
       abs(a[7]-a[6])==1||abs(a[8]-a[5])==1||abs(a[9]-a[4])==1||abs(a[4]-a[2])==1||abs(a[3]-a[1])==1||
       abs(a[4]-a[0])==1||abs(a[5]-a[1])==1||abs(a[6]-a[0])==1||abs(a[7]-a[5])==1||abs(a[6]-a[8])==1||
       abs(a[8]-a[4])==1||abs(a[5]-a[9])==1||abs(a[9]-a[3])==1)continue;
      sum++;}while(next_permutation(a,a+10));
      cout<<sum<<endl;}
int main()
{
    solve();
    return 0;
}
//答案1580

四平方和


题意：

输出一个数把它拆分为四个升序数的平方之和。并输出。

思路：

第一想法暴力枚举，借鉴了一位大佬的代码思想

链接
代码

#include
using namespace std;
int n;
void solve()
{

    for(int a=0;4*a*a<n;a++)
    {
        for(int b=a;3*b*b<n-a*a;b++)
        {

            for(int c=b;2*c*c<n-a*a-b*b;c++)
            {
                int d=sqrt(n-a*a-b*b-c*c);
                if(a*a+b*b+c*c+d*d==n)
                {
                    cout<<a<<" "<<b<<" "<<c<<" "<<d<<endl;
                    return;
                }
            }
        }
    }
}
int main()
{
    while(cin>>n)
    {
        solve();
    }
    return 0;
}

交换瓶子


题意：

输出一串数字，问至少需要要多少次操作可以按1-n升序排列。

思路：

直接遍历所有数组，如果该数组的值与该数组的位置不同，则进行一个交换操作。

代码

#include
using namespace std;
int a[11000];
int n;
int main()
{
    while(cin>>n)
    {
        int sum=0;
        for(int i=1;i<=n;i++)
        {
            cin>>a[i];
        }
        for(int i=1;i<=n;i++){
        if(a[i]!=i)
        {
            swap(a[i],a[a[i]]);
            sum++;
        }}
        cout<<sum<<endl;
    }return 0;
}

最大比例

代码

#include
using namespace std;
typedef long long ll;
const int N=200;
int n;
ll a[N],b[N],c[N];
ll gcd(ll a,ll b)
{
    if(b==0)return a;
    return gcd(b,a%b);
}
ll gcd_sub(ll a,ll b)//辗转相减的另一种使用
{
    if(a==b)return a;//这里一定会 出现这种情况的 因为我们的b和a是倍数关系
    if(a>b)return gcd_sub(b,a/b);
    else return gcd_sub(b,a);//保证a>b
}
int main()
{
    while(cin>>n){
    for(int i=0;i<n;i++)
    {cin>>c[i];}
    sort(c,c+n);
    int sum=0;
    for(int i=1;i<n;i++)
    if(c[i]!=c[i-1])
    {
        ll d=gcd(c[i],c[i-1]);
        a[sum]=c[i]/d;
        b[sum]=c[i-1]/d;
        sum++;
    }
    ll up=a[0],down=b[0];
    for(int i=1;i<sum;i++)
    {
        up=gcd(up,a[i]);
        down=gcd(down,b[i]);
    }
    cout<<up<<'/'<<down<<endl;}
    return 0;
}

如果觉得写的不错点个赞吧，比心！