动态规划（Leetcode198--打家劫舍、Leetcode121--买卖股票的最佳时机）

动态规划（Leetcode198–打家劫舍、Leetcode121–买卖股票的最佳时机）

动态规划，英文描述为Dynamic programming. 是一种可以把原始问题分解为若干相关联的子解问题，并通过求取和保存子问题的解，获得原问题的解。

编程语言：python

作者：黑暗主宰

邮箱：[email protected]

动态规划

博主也是一个入门算法的小白，对于网上大佬们提供的各种的动态规划代码表示很惊艳。动态规划主要应用于解决子问题重叠的情况，最主要的是找到状态转移方程，然后代码就非常好写了。说是这么说，小伙伴们还是要多练习，多总结，才可以很好的解决此类型的题。然后博主也是在路上，不能分享整个动态规划的框架，只能分享一下我遇到一个题是怎么解出来的，还有为啥没有解出来，大佬勿喷！

Leetcode198–打家劫舍

leetcode198题，打家劫舍；

下面只写一下题目的题干，具体的，小伙伴们自己点进去看。

题目描述：

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

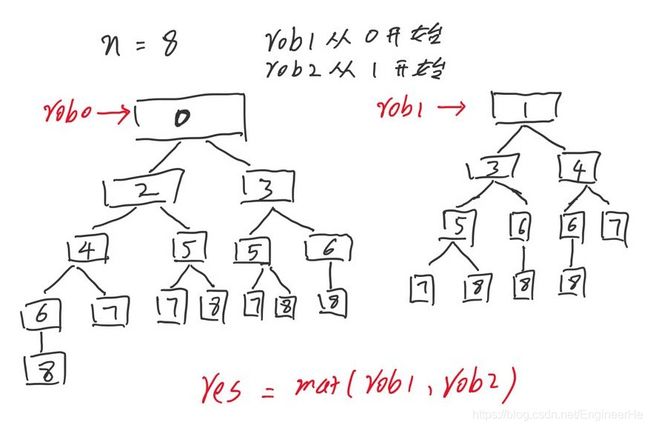
拿到这道题，我刚开始并没有想到动态规划的做法（还没有完全吃透XD），我用的是递归的方法，如下图，小偷1从0开始，然后他可以偷第2家和第3家（为什么他不直接偷第四家，那除非他傻，直接投第四家，漏了第二家，肯定是亏了呀），然后依次类推；同样的小偷2从第一家开始偷，最后比较一下那个那个小偷的大，返回结果。

然后就如上面的图一样，我们要找到递归的出口，出口就是当n>8的时候直接返回0，具体的看一下代码：

def rob(nums):
	l = len(nums)
	rob1 = 0
	rob2 = 0

	def d(n):
        # 递归出口
		if n >= l:
			return 0
        # 循环递归
		return max(d(n+2) + nums[n], d(n+3) + nums[n])
        
	return max(d(0), d(1))
        

这样的解法，就如图上的一样，会有有很多的冗余的内存，所以当n比较大的时候，会非常的耗时。所以在leetcode提交会TLE

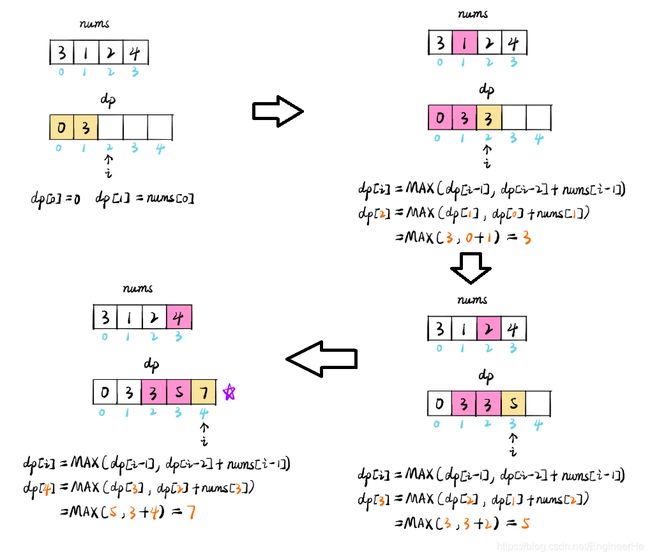
下面是动态规划的解法，首先就是尽可能的找到状态转移方程，就和 leetcode70-爬楼梯 类似，正向不行就反着来，假如我们现在有n家，我们想知道 dp[n]，是不是只要知道 dp[n-1]和 dp[n-2]就可以得到 dp[n]=max(dp[n-1], dp[n-2]+nums[n])， 所里动态规划的状态转移方程就可以得到 dp[n] = max(dp[n-1], dp[n-2] + nums[n])，具体的看下图¹

这里为了好写代码，设 dp[0]=0, dp[1]=0，然后整体代码如下

def rob(nums):
	res = [0,0]
	for num in nums:
		tmp = max((res[0] + num), res[1])
		res[0], res[1] = res[1], tmp    
	return res[-1]

Leetcode121–买卖股票的最佳时机

Leetcode121 买卖股票的最佳时机

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

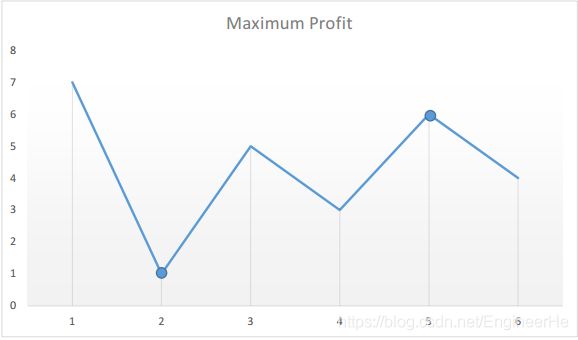
要获取做大的利润，要是可以在过程中记录最小的一个值，然后在记录最大的一个值，两者相减就可以啦，这里引用一个图²，即找到最小的谷值和最大的峰值，这里需要注意一定是买入后才可以卖出，所以不能直接求数字的maxnum和minnum

上述思路题解代码如下：

def maxProfit(prices):
	if not prices:
		return 0
	buy = prices[0]
	maxdiff = 0
	for price in prices:
		if price-buy < 0:
			buy = price
		else:
			diff = price - buy
			maxdiff = max(diff, maxdiff)
	return maxdiff

使用动态规划的解法

首先要确定状态转移方程；同样的反过来推导，假如要知道n天里的最大利润，如果知道第n-1天的最大利润，那我们用今天的价格减去前面n-1天的最小值，是不是就得到了第n天的利润，然后计算 max(profit[n-1], profit[n])，就可以得到n天范围内的最大利润，所以 maxProfit = max(profit[n-1], profit[n])。

代码如下：

def maxProfit(prices):
	if (len(prices)<=1):
		return 0
	min_price = prices[0]
	max_price = 0
	for price in prices:
		min_price = min(min_price, price)
		max_price = max(max_price, price-min_p)
	return max_price

欢迎大家关注我的个人公众号，同样的也是和该博客账号一样，专注分享技术问题，我们一起学习进步

注： 文中有写错的地方，欢迎大家不吝指正！！!

---

1. https://leetcode-cn.com/problems/house-robber/solution/hua-jie-suan-fa-198-da-jia-jie-she-by-guanpengchn ↩︎

2. https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-by-leetcode ↩︎