权值衰减weight decay的理解

1. 介绍

权值衰减weight decay即L2正则化，目的是通过在Loss函数后加一个正则化项，通过使权重减小的方式，一定减少模型过拟合的问题。

• L1正则化：即对权重矩阵的每个元素绝对值求和，$\lambda \ast ||W||$
• L2正则化：即对权重矩阵的每个元素求平方和（先平方，后求和）:
  $$1/2\ast \lambda \ast ||W|{|}^2$$

注意：正则化项不需要求平均数，因为权重矩阵和样本数量无关，只是为了限制权重规模。

L1损失函数：最小化绝对误差，因此L1损失对异常点有较好的适应更鲁棒，不可导，有多解，解的稳定性不好。关于L1损失函数的不连续的问题，可以通过平滑L1损失函数代替：

L2损失函数：最小化平方误差，因此L2损失对异常点敏感，L2损失函数会赋予异常点更大的损失值和梯度，调整网络参数向减小异常点误差的方向更新，因此容易造成训练的不稳定和发散。仅有一解，解的稳定更好

2. weight decay的作用

从直观上讲，L2正则化(weight decay)使得训练的模型在兼顾最小化分类（或其他目标）的Loss的同时，使得权重w尽可能地小，从而将权重约束在一定范围内，减小了模型的复杂度；同时，如果将w约束在一定范围内，也能够有效防止梯度爆炸。

3. Pytorch中的L2正则项——weight decay

L2正则项本质上相当于是权值衰减，这是因为目标函数为:
$Obj=Cost+Regularization$, 在梯度下降公式中:

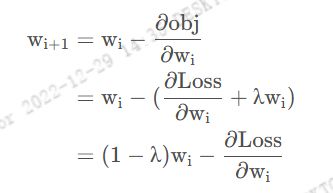
由于这里的正则化系数$\lambda$是一个介于0 到1之间数，因此可以看出，与不加正则项的梯度下降公式: $w_{i+1}=w_i-\frac{\partial Loss}{\partial w_i}$ 相比，相当于是做了一个权值的下降

Pytorch中的 weight decay 是在优化器中实现的，在优化器中加入参数weight_decay=即可，参数中的weight_decay等价于正则化系数$\lambda$。例如下面的两个随机梯度优化器，一个是没有加入正则项，一个加入了正则项，区别仅仅在于是否设置了参数weight_decay的值：

optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)

4. weight decay效果示例

hello_pytorch_DIR = os.path.abspath(os.path.dirname(__file__)+os.path.sep+".."+os.path.sep+"..")
sys.path.append(hello_pytorch_DIR)

from tools.common_tools import set_seed
from torch.utils.tensorboard import SummaryWriter

set_seed(1)  # 设置随机种子
n_hidden = 200
max_iter = 2000
disp_interval = 200
lr_init = 0.01


# ============================ step 1/5 数据 ============================
def gen_data(num_data=10, x_range=(-1, 1)):

   w = 1.5
   train_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
   train_y = w*train_x + torch.normal(0, 0.5, size=train_x.size())
   test_x = torch.linspace(*x_range, num_data).unsqueeze_(1)
   test_y = w*test_x + torch.normal(0, 0.3, size=test_x.size())

   return train_x, train_y, test_x, test_y


train_x, train_y, test_x, test_y = gen_data(x_range=(-1, 1))


# ============================ step 2/5 模型 ============================
class MLP(nn.Module):
   def __init__(self, neural_num):
       super(MLP, self).__init__()
       self.linears = nn.Sequential(
           nn.Linear(1, neural_num),
           nn.ReLU(inplace=True),
           nn.Linear(neural_num, neural_num),
           nn.ReLU(inplace=True),
           nn.Linear(neural_num, neural_num),
           nn.ReLU(inplace=True),
           nn.Linear(neural_num, 1),
       )

   def forward(self, x):
       return self.linears(x)


net_normal = MLP(neural_num=n_hidden)
net_weight_decay = MLP(neural_num=n_hidden)

# ============================ step 3/5 优化器 ============================
optim_normal = torch.optim.SGD(net_normal.parameters(), lr=lr_init, momentum=0.9)
optim_wdecay = torch.optim.SGD(net_weight_decay.parameters(), lr=lr_init, momentum=0.9, weight_decay=1e-2)

# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()

# ============================ step 5/5 迭代训练 ============================

writer = SummaryWriter(comment='_test_tensorboard', filename_suffix="12345678")
for epoch in range(max_iter):

   # forward
   pred_normal, pred_wdecay = net_normal(train_x), net_weight_decay(train_x)
   loss_normal, loss_wdecay = loss_func(pred_normal, train_y), loss_func(pred_wdecay, train_y)

   optim_normal.zero_grad()
   optim_wdecay.zero_grad()

   loss_normal.backward()
   loss_wdecay.backward()

   optim_normal.step()
   optim_wdecay.step()

   if (epoch+1) % disp_interval == 0:

       # 可视化
       for name, layer in net_normal.named_parameters():
           writer.add_histogram(name + '_grad_normal', layer.grad, epoch)
           writer.add_histogram(name + '_data_normal', layer, epoch)

       for name, layer in net_weight_decay.named_parameters():
           writer.add_histogram(name + '_grad_weight_decay', layer.grad, epoch)
           writer.add_histogram(name + '_data_weight_decay', layer, epoch)

       test_pred_normal, test_pred_wdecay = net_normal(test_x), net_weight_decay(test_x)

       # 绘图
       plt.scatter(train_x.data.numpy(), train_y.data.numpy(), c='blue', s=50, alpha=0.3, label='train')
       plt.scatter(test_x.data.numpy(), test_y.data.numpy(), c='red', s=50, alpha=0.3, label='test')
       plt.plot(test_x.data.numpy(), test_pred_normal.data.numpy(), 'r-', lw=3, label='no weight decay')
       plt.plot(test_x.data.numpy(), test_pred_wdecay.data.numpy(), 'b--', lw=3, label='weight decay')
       plt.text(-0.25, -1.5, 'no weight decay loss={:.6f}'.format(loss_normal.item()), fontdict={'size': 15, 'color': 'red'})
       plt.text(-0.25, -2, 'weight decay loss={:.6f}'.format(loss_wdecay.item()), fontdict={'size': 15, 'color': 'red'})

       plt.ylim((-2.5, 2.5))
       plt.legend(loc='upper left')
       plt.title("Epoch: {}".format(epoch+1))
       plt.show()
       plt.close()

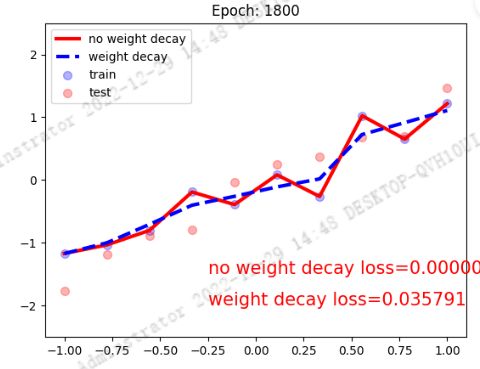
红色曲线为没有 weight decay 的结果，蓝色虚线为加入 weight decay 的训练结果，可以看到加入后能够非常有效的缓解过拟合现象。

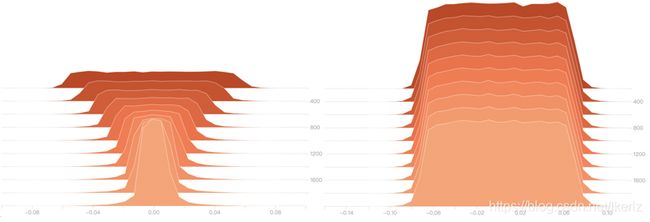
下图为第二层的权值柱状图，左边为加入正则项，右边为没有加正则项，可以看出，左边的权值确实有一个递减的趋势，而右边几乎是保持不变的状态。

参考：深度之眼Pytorch框架训练营第四期——正则化之weight decay