第十一届蓝桥杯国赛C++B组题解（A - J）

第十一届蓝桥杯国赛C++B组

美丽的2

题目地址：https://www.lanqiao.cn/problems/1018/learning/

难度：简单

知识点：

• 模拟
• 枚举

【题目描述】

​ $1-2020$ 中有多少个数中含有数字2

【解题思路】

范围很小，直接暴力判断每个数即可。最后的答案为563

AC_Code

#include 
using namespace std;
int main() {
    int ans = 0;
    for (int i = 1; i <= 2020; i ++) {
        bool ok = false;
        int j = i; while(j) ok |= (j % 10 == 2), j /= 10;
        ans += ok;
    }
    cout << ans << "\n"; //563
}

扩散

题目地址：https://www.lanqiao.cn/problems/1019/learning/

难度：简单

知识点：

• 宽度优先搜索BFS
• 模拟

【题目描述】

​ 有一个无限大的方格纸，现在有四个黑点（0， 0），（2020，11），（11，14），（2000，2000），其余都是白色的。每过一分钟，黑色的点会向四周（上，下，左，右）扩散一点使其也变为黑色，如果原来是黑色则还是黑色。问过了2020分钟后，画布上有多少个黑色的。

【解题思路】

​ 利用宽度优先搜索实现扩散即可。为了防止出现负数下标，我们将四个点向右上方偏移2020个单位。最后的答案为20312088

AC_Code

#include 
using namespace std;
using LL = long long;
const int N = 6500;
bool mp[N][N];
int dx[] = {-1, 0, 1, 0};
int dy[] = {0, 1, 0, -1};
// (0, 0) (2020, 11) (11, 14) (2000, 2000)
PII start[] = {
    {0 + 2020, 0 + 2020},
    {2020 + 2020, 11 + 2020},
    {11 + 2020, 14 + 2020},
    {2000 + 2020, 2000 + 2020}
};
vector<PII> stk, tmp;
int main() {
    for (int i = 0; i < 4; i ++) {
        auto t = start[i];
        stk.push_back(t);
        mp[t.first][t.second] = true;
    }
    for (int i = 1; i <= 2020; i ++) {
        for (auto t : stk) {
            for (int j = 0; j < 4; j ++) {
                int x = t.first + dx[j], y = t.second + dy[j];
                if(!mp[x][y]) {
                    mp[x][y] = true;
                    tmp.push_back({x, y});
                }
            }
        }
        stk = tmp; tmp.clear();
    }
    int ans = 0;
    for (int i = 0; i < N; i ++) {
        for (int j = 0; j < N;j ++) {
            ans += mp[i][j];
        }
    }
    cout << ans << '\n'; // 20312088
}

阶乘约数

题目地址：https://www.lanqiao.cn/problems/1020/learning/

难度：中等

知识点：

• 约数
• 数论

【题目描述】

​ 求出$100!$（100的阶乘），有多少个正约数

【解题思路】

​ 根据算术基本定理：$N=p_1^{a_1}\ast p_2^{a_2}\dots p_i^{a_i},N\in$ 正整数，这里的$p_1,p_2,\dots p_i$为递增的质数

​ 又根据约数个数定理：一个正整数的约数个数就是$f(n)={\prod }_{j=1}^i(a_j+1)=(a_1+1)\ast (a_2+1)\dots (a_i+1)$其中，$a_1,a_2,...,a_i$为上述$p_1,p_2,...,p_i$的指数。现在的问题转换为求：$100!$的质因数及其个数。那这样的话就比较好求了，对于一个小于$n$的质数$p$来说，$n!$中包含$\lfloor \frac{n}{p}\rfloor$个$p$，$\lfloor \frac{n}{p^2}\rfloor$个$p^2$，··· 直到没有。

最后的答案为39001250856960000

AC_Code

#include 
using namespace std;
using LL = long long;
const int N = 110, n = 100;
int cnt, p[N];
bool st[N];
int main() {
    for (int i = 2; i <= n; i ++) {
        if(!st[i]) p[++ cnt] = i;
        for (int j = i + i; j <= n; j += i) st[j] = true;
    }
    LL ans = 1;
    for (int i = 1; i <= cnt; i ++) {
        int t = p[i];
        int s = 0;
        for (int j = t; j <= n; j *= t) s += n / j;
        ans *= (s + 1);
    }
    cout << ans << "\n"; // 39001250856960000
}

本质上升序列

题目地址：https://www.lanqiao.cn/problems/1021/learning/

难度：中等

知识点：

• 动态规划

【题目描述】

有一个长度为200的字符串（见下面代码）。问上升的子序列有多少个？注：相同的子序列算同一个即使位置不同。例如：lanqiao，可以去出两个ao，但只算一个。

【解题思路】

​ 由于长度有200，用暴力的方法枚举出所有的子序列是不现实的。所有考虑优雅的暴力：动态规划。

​ 定义：$f_i$为以$s_i$结尾的本质上升子序列的个数

​ 状态转移：$f_i=\sum (f_j\leftarrow j\in [0,i)\bigcap s_i>s_j)-\sum (f_j\leftarrow j\in [0,i)\bigcap s_i==s_j)$

如果发现存在与前面相等的字符$j$时，一定要减去相应的$f_j$，不然$f_i$就多加了一个$f_j$的数量！！！ 最后的答案为3616159

AC_Code

#include 
using namespace std;
const int N = 210;
int f[N];
string s = "tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";

int main() {
    for (int i = 0; i < 200; i ++) {
        f[i] = 1;
        for (int j = 0; j < i;j ++) {
            if(s[i] > s[j]) f[i] += f[j];
            else if(s[i] == s[j]) f[i] -= f[j];
        }
    }    
    int ans = 0;
    for (int i = 0; i < 200; i ++) ans += f[i];
    cout << ans << '\n'; // 3616159
}

玩具蛇

题目地址：https://www.lanqiao.cn/problems/1022/learning/

难度：简单

知识点：

• 深度优先搜索

【题目描述】

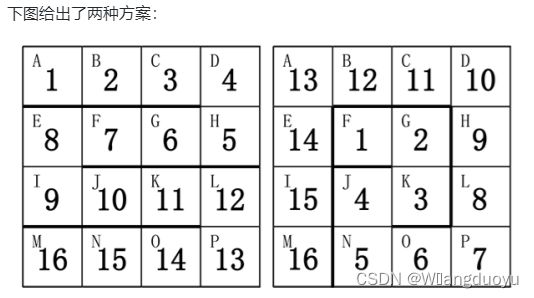
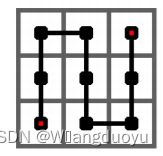
​ 有一个长度为16节的玩具蛇，把他放进编号为A-P的正方形中有多少中方案？

【解题思路】

​ 枚举起点，然后进行深度优先搜索。最后的答案为552

AC_Code

#include 
using namespace std;
const int N = 5;
bool st[N][N];
int dfs(int u, int x, int y) {
    if(u == 16) {
        return 1;
    }
    int t = 0;
    st[x][y] = true;
    static int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
    for (int i = 0; i < 4; i ++) {
        int xx = x + dx[i], yy = y + dy[i];
        if(xx >= 1 && xx <= 4 && yy >= 1  && yy <= 4 && !st[xx][yy]) {
            t += dfs(u + 1, xx, yy);
        }
    }
    st[x][y] = false;
    return t;
}

int main() {
    int ans = 0;
    for (int i = 1; i <= 4; i ++)
        for (int j = 1; j <= 4; j ++)
            ans += dfs(1, i, j);
    cout << ans << '\n'; // 552
}

皮亚诺曲线距离

题目地址：https://www.lanqiao.cn/problems/1023/learning/

难度：困难

知识点：

• 坐标变换
• 递归
• 分治

【题目描述】

​ 皮亚诺曲线总是由左下角走到右上角，一阶：

二阶：

​ 现在给出一个$k$阶，左下角坐标为：（0，0），右上角坐标为：$（3^k-1,3^k-1）$以及两个点坐标，求出这两个坐标沿着皮亚诺曲线走，距离是到多少？

【解题思路】

​ 可以从起点沿着皮亚诺曲线编号，利用递归分治实现由坐标推到编号，最后答案就是两者编号相减的绝对值。具体分析见下图。

• 另外注意，此题最后一个数据点会爆long long，故开int128，使用int128需要手写输人和输出。不要使用$y1$变量，否则编译错误

AC_Code

#include 
using namespace std;
typedef __int128 LL;
long long n, x1, yy, x2, y2;

LL qpow(LL a, long long b) {
    LL ans = 1;
    while (b) {
        if(b & 1) ans = ans * a;
        b >>= 1; a = a * a;
    }
    return ans;
}

int d[3][3] = {
    {0, 1, 2},
    {5, 4, 3},
    {6, 7, 8}
};

LL get(long long n, long long x, long long y) {
    if(!n) return 0;
    LL len = qpow(3, n - 1), num = len * len;
    int r = x / len, c  = y / len;
    int pos = d[r][c];
    LL x1 = 0, yy = 0;
    switch(pos) {
        case 0 :
            x1 = x, yy = y;
            break;
        case 1:
            x1 = len - x - 1, yy = y - len;
            break;
        case 2: 
            x1 = x, yy = y - 2 * len;
            break;
        case 3:
            x1 = x - len, yy = 3 * len - y - 1;
            break;
        case 4: 
            x1 = 2 * len - x - 1, yy = 2 * len - y - 1;
            break;
        case 5:
            x1 = x - len, yy = len - y - 1;
            break;
        case 6: 
            x1 = x - 2 * len, yy = y;
            break;
        case 7:
            x1 = 3 * len - x - 1, yy = y - len;
            break;
        case 8:
            x1 = x - 2 * len, yy = y - 2 * len;
            break;
    }
    return num * pos + get(n - 1, x1, yy);
}

void print(LL t) {
    if(t < 0) putchar('-'), t = -t;
    if(t > 9) print(t / 10);
    putchar('0' + t % 10);
}

int main() {
    scanf("%lld%lld%lld%lld%lld", &n, &x1, &yy, &x2, &y2);
    LL p1 = get(n, x1, yy), p2 = get(n, x2, y2);
    if(p1 > p2) swap(p1, p2);
    print(p2 - p1);
}

游园安排

题目地址：https://www.lanqiao.cn/problems/1024/learning/

难度：困难

知识点：

• 最长上升子序列
• 贪心优化
• 动态规划求具体方案

【问题描述】

​ 有一串字符串，包含若干个名字，每个名字开头字母为大写，后面接着若干个小写字母。问这些名字的最长严格上升子序列的是什么？

【解题思路】

​ 为了确保严格上升，可以先把名字换算成27进制的数字。对于数字序列的严格上升子序列求法，可以利用动态规划。由于本题数据范围较大，故采用贪心的思想优化LIS（最长上升子序列）的过程。

具体优化如下：

首先，定义$a_1\dots a_n$为原始序列，$d$为当前的严格上升子序列，$len$为子序列的长度，那$d_{len}$就是长度为$len$的不下降序列末尾元素。初始化： $d_1=a_1,len=1$现在我们已知最长上升子序列长度为 1，那么我们让 $i$从 2 到 $n$ 循环，依次求出前 $i$个元素的最长上降子序列的长度，循环的时候我们只需要维护好 $d$这个数组还有 $len$就可以了。关键在于如何维护。

• 考虑进来一个元素
  1. 元素大于$d_{len}$，直接将该元素插入到$d$ 序列的末尾。
  2. 元素小于等于$d_{len}$，在$d$找到第一个大于等于它的元素，替换

此外，再用一个数组$f_i$存储以$a_i$结尾的最长严格上升子序列的长度。最后再逆序推出序列即可。

AC_Code

#include 
using namespace std;
using LL = long long;
string s;
vector<string> g;
LL get(string s) {
    LL res = 0;
    for (auto ch : s) {
        if(ch >= 'a' && ch <= 'z') res = res * 27 + ch - 'a' + 1;
        if(ch >= 'A' && ch <= 'Z') res = res * 27 + ch - 'A' + 1;
    }
    for (int i = s.size(); i < 10; i ++) res *= 27;
    return res;
}
int f[1000100];
int main() {
    cin >> s;
    int m = 0;
    for (int i = 0; i < s.size(); i ++) {
        string tmp = ""; tmp += s[i];
        int t = i + 1;
        while (t < s.size() && s[t] >= 'a' && s[t] <= 'z') tmp += s[t ++];
        i = t - 1;
        g.push_back(tmp);
    }
    vector<LL> a;
    for (auto t : g) a.push_back(get(t));
    int cnt = 0; 
    vector<LL> stk;
    stk.push_back(a[0]); f[0] = 1;

    for (int i = 1; i < a.size(); i ++) {
        if(stk.back() < a[i]) stk.push_back(a[i]), f[i] = stk.size();
        else {
            auto t = lower_bound(stk.begin(), stk.end(), a[i]) - stk.begin();
            f[i] = t + 1;
            stk[t] = a[i];
        }
    }
    LL maxv = 1e18;
    vector<int> ans;
    for (int i = stk.size(), j = a.size() - 1; i ; i --) {
        while(j > 0 &&( f[j] != i || maxv < a[j])) j --;
        maxv = a[j]; ans.push_back(j);
    }
    for (int i = ans.size() - 1; i + 1; i --) cout << g[ans[i]];
}

答疑

题目地址：https://www.lanqiao.cn/problems/1025/learning/

难度：简单

知识点：

• 贪心
• 结构体排序

【题目描述】

​ 有$n$个学生，现在轮流去老师办公室问问题。对于第$i$个学生来说，进房间要花$s_i$的时间，问问题要花$a_i$的时间，这是老师在班群发一个消息（需要的时间忽略），然后出房间花费$e_i$。注意：只有当学生离开了办公室后，下一位学生才可以进入。问如何安排这$n$个学生，是的老师在班群发消息的时刻之和最小。

【解题思路】

很容易想到贪心求解。只需要将 $s+a+e$ 降序排列就是答案。

我们来证明这个贪心策略：现在有任意两个学生 $i$ 和$j$ ：

1. $i$ 在前 $j$ 在后，$w_1=s_i+a_i+(s_i+a_i+e_i+s_j+a_j)$
2. $j$ 在前 $i$ 在后，$w_2=s_j+a_j+(s_j+a_j+e_j+s_i+a_i)$

假设，策略1花费较少，则有$w_1-w_2<0$， 也就是$s_i+a_i+e_i<s_j+a_j+e_j$ 故此贪心策略得证。

AC_Code

#include 
using LL = long long;
const int N = 1010;
struct student{
    int s, a, e;
    bool operator < (const student &b) {
        return s + a + e < b.s + b.a + b.e;
    }
};
student a[N];
int main() {
    int n;
    std::cin >> n;
    for (int i = 1; i <= n; i ++)  std::cin >> a[i].s >> a[i].a >> a[i].e;
    std::sort(a + 1, a + 1 + n);
    LL ans = 0, t = 0;
    for (int i = 1; i <= n; i ++) {
        t += a[i].s + a[i].a;
        ans += t;
        t += a[i].e;
    }
    std::cout << ans << "\n";
}

出租车

题目地址：https://www.lanqiao.cn/problems/1026/learning/

难度：困难

知识点：

• 最短路
• Dijkstra

【题目描述】

​ 有$N$个东西走向的道路$H_1,\dots H_N$， $M$个南北走向的道路$S_1\dots S_M$，$H_1$和$S_1$的交点为(1, 1)。向南遇到的路口与其的距离分别为$h_1\dots h_{n-1}$，向东遇到的路口与其的距离分别为$w_1\dots w_{m-1}$。每个路口都有一个红绿灯，刚开始，南北向绿灯，东西向红灯，南北向（i，j）绿灯持续$g_{i,j}$，东西向绿灯持续$r_{i,j}$。红灯只可以右转，只能再红绿灯掉头（红灯也可以）。现在有$q$个订单，小蓝家在两个路口的中点，即$(x_1,y_1）,（x_2,y_2）$中点的右侧。每个订单给出四个坐标，表示起点和终点的两个路口的坐标，也都是在两个路口中点出发，中点结束。

【解题思路】

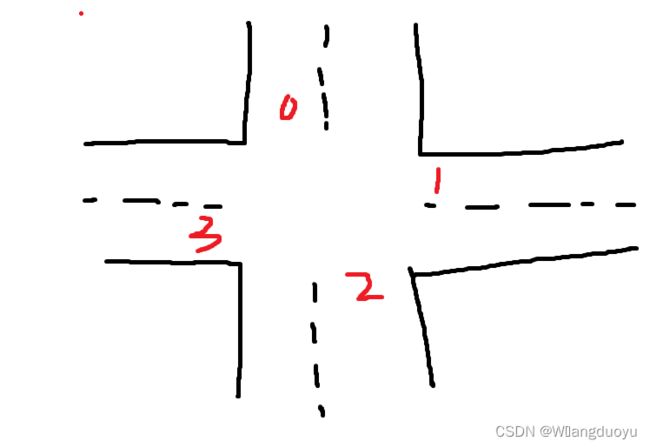
思路来自：大佬的博客

​ 把路口拆成四个点。表示车开到如图所示的点需要的时间。然后跑最短路即可。

AC_Code

#include 
using namespace std;

const int maxn = 105;
const int xx[4] = { -1, 0, 1, 0 };
const int yy[4] = { 0, 1, 0, -1 };
const double INF = 10000000000005ll;

bool vis[maxn][maxn][4];
double T = 0, dis[maxn][maxn][4];
struct node { int x, y, f; } a[6];
inline bool operator ==(node a, node b) { return a.x == b.x && a.y == b.y; }

struct Node { double d; node x; };
inline bool operator <(Node a, Node b) { return a.d < b.d; }
inline bool operator >(Node a, Node b) { return a.d > b.d; }

int N, M, Q, h[maxn], w[maxn], g[maxn][maxn], r[maxn][maxn];

inline double wait(node u, double tim) {
    tim += T;
    tim -= floor(tim / (g[u.x][u.y] + r[u.x][u.y])) * (g[u.x][u.y] + r[u.x][u.y]);
    if (u.f & 1) { // 东西向 初始红
        if (abs(tim - g[u.x][u.y]) < 1e-6) return 0;
        if (tim > g[u.x][u.y]) return 0;
        else return g[u.x][u.y] - tim;
    }
    else {
        if (abs(tim - g[u.x][u.y]) < 1e-6) return r[u.x][u.y];
        if (tim < g[u.x][u.y]) return 0;
        else return r[u.x][u.y] + g[u.x][u.y] - tim;
    }
}

inline double getDistance(node a, node b) {
    return (a.x == b.x) ? abs(w[a.y] - w[b.y]) : abs(h[a.x] - h[b.x]);
}

double Calc() {
    if (a[0] == a[2] && a[1] == a[3]) return 0;
    for (int i = 1; i <= N; ++i)
        for (int j = 1; j <= M; ++j)
            for (int k = 0; k < 4; ++k) {
                dis[i][j][k] = INF;
                vis[i][j][k] = 0;
            }
    a[1].f = (a[0].x == a[1].x) ? ( (a[1].y > a[0].y) ? 3 : 1 ) : ( (a[1].x > a[0].x) ? 0 : 2 );
    dis[a[1].x][a[1].y][a[1].f] = getDistance(a[0], a[1]) * 0.5;
    priority_queue < Node, vector<Node>, greater<Node> > Q;
    Node f;
    f.d = dis[a[1].x][a[1].y][a[1].f];
    f.x = a[1];
    Q.push(f);
    while (!Q.empty()) {
        node u = Q.top().x, v;
        Q.pop();
        if (vis[u.x][u.y][u.f]) continue;
        vis[u.x][u.y][u.f] = 1;
        // 掉头
        v.x = u.x + xx[u.f], v.y = u.y + yy[u.f], v.f = (u.f + 2) % 4;
        if (v.x >= 1 && v.x <= N && v.y >= 1 && v.y <= M) {
            if (dis[v.x][v.y][v.f] > dis[u.x][u.y][u.f] + getDistance(u, v)) {
                dis[v.x][v.y][v.f] = dis[u.x][u.y][u.f] + getDistance(u, v);
                f.d = dis[v.x][v.y][v.f];
                f.x = v;
                Q.push(f);
            }
        }
        // 右转
        v.x = u.x + xx[(u.f + 3) % 4], v.y = u.y + yy[(u.f + 3) % 4], v.f = (u.f + 1) % 4;
        if (v.x >= 1 && v.x <= N && v.y >= 1 && v.y <= M) {
            if (dis[v.x][v.y][v.f] > dis[u.x][u.y][u.f] + getDistance(u, v)) {
                dis[v.x][v.y][v.f] = dis[u.x][u.y][u.f] + getDistance(u, v);
                f.d = dis[v.x][v.y][v.f];
                f.x = v;
                Q.push(f);
            }
        }
        // 左转
        double t = wait(u, dis[u.x][u.y][u.f]);
        v.x = u.x + xx[(u.f + 1) % 4], v.y = u.y + yy[(u.f + 1) % 4], v.f = (u.f + 3) % 4;
        if (v.x >= 1 && v.x <= N && v.y >= 1 && v.y <= M) {
            if (dis[v.x][v.y][v.f] > dis[u.x][u.y][u.f] + getDistance(u, v) + t) {
                dis[v.x][v.y][v.f] = dis[u.x][u.y][u.f] + getDistance(u, v) + t;
                f.d = dis[v.x][v.y][v.f];
                f.x = v;
                Q.push(f);
            }
        }
        // 直行
        t = wait(u, dis[u.x][u.y][u.f]);
        v.x = u.x + xx[(u.f + 2) % 4], v.y = u.y + yy[(u.f + 2) % 4], v.f = u.f;
        if (v.x >= 1 && v.x <= N && v.y >= 1 && v.y <= M) {
            if (dis[v.x][v.y][v.f] > dis[u.x][u.y][u.f] + getDistance(u, v) + t) {
                dis[v.x][v.y][v.f] = dis[u.x][u.y][u.f] + getDistance(u, v) + t;
                f.d = dis[v.x][v.y][v.f];
                f.x = v;
                Q.push(f);
            }
        }
    }
    a[3].f = (a[2].x == a[3].x) ? ( (a[3].y > a[2].y) ? 3 : 1 ) : ( (a[3].x > a[2].x) ? 0 : 2 );
    return dis[a[3].x][a[3].y][a[3].f] - getDistance(a[2], a[3]) * 0.5;
}

int main() {
    cin >> N >> M;
    for (int i = 2; i <= N; ++i) cin >> h[i];
    for (int i = 2; i <= M; ++i) cin >> w[i];
    for (int i = 1; i <= N; ++i)
        for (int j = 1; j <= M; ++j) cin >> g[i][j];
    for (int i = 1; i <= N; ++i)
        for (int j = 1; j <= M; ++j) cin >> r[i][j];
    cin >> a[0].x >>  a[0].y >> a[1].x >> a[1].y;
    a[4] = a[0], a[5] = a[1];
    for (cin >> Q; Q--; ) {
        cin >> a[2].x >> a[2].y >> a[3].x >> a[3].y;
        T += Calc();
        a[0] = a[2], a[1] = a[3];
        cin >> a[2].x >> a[2].y >> a[3].x >> a[3].y;
        T += Calc();
        a[0] = a[2], a[1] = a[3];
    }
    a[2] = a[4], a[3] = a[5];
    T += Calc();
    printf("%.1lf", T);
    return 0;
}

质数行者

题目地址：https://www.lanqiao.cn/problems/1027/learning/

难度：困难

知识点：

• 动态规划
• 计数类，排列组合
• 逆元

【题目描述】

​ 从$（1，1，1）$走到$（n，m，w）$，途中不能经过 $(r_1,c_1,h_1)，(r_2,c_2,h_2)$。有多少种方案。

【解题思路】

思路来自：大佬的博客

​ 题目要求的是从$(1,1,1)$走到$(n,m,w)$且不经过两个陷阱的点的方案总数。首先我们不考虑陷阱的情况，然后在所有的答案中减去陷阱点的情况就行了。

考虑直接从(1,1,1)到(n,m,w)的情况。我们可以把这个三维的过程分成三个一维的质数分解方案，然后再将三个一维的方案合并成一个三维的方案数就行了。
考虑一维的情况从1到n只能走质数步，一共有多少方案数？

如果只求这个答案一维dp就够了，$dp[i]$表示到达$i$时一共有多少种方案数。然而我们还要考虑合并的情况，所以这里我们设计的状态为$dp[i][j]$表示走到i时，一共走了$j$步的方案总数。

转移方程为：$dp[i][j]+=dp[i-k][j-1]$//k为某个质数值

一维的情况解决了，怎么合并为二维呢？当我们确定了在x轴上走的每一步的顺序，加入y轴的情况就相当于我往x轴的步骤中插入我在y轴走的步数。

比如：当n=5，m=6时，我要在x轴上走4步，在y轴上走5步。那么在x轴走的方案就只有 2 2一种，y轴的方案有(5),(2,3),(3,2)三种。把y轴加入进x轴，就相当于是把y中的数字打包插入x的空隙之中。也相当于是把x维走的情况和y维走的情况作一个排列然后再消去原本已经确定的步骤的影响。

设$X[i]$表示$x$维度到达$n$，且走了$i$步的方案数，$Y[i]$表示$y$维度到达$m$，且走了$i$步的方案数，$XY[i]$表示$X$维到达$n$，$Y$维到达$m$时，一共走了$i$部的方案数。可以知道的是$X[i]=dp[n][i],Y[i]=dp[m][i]$（dp含义见上）。

$XY[i+j]+=X[i]\ast Y[j]\ast (i+j)!/(i!)/(j!)$
$x$维走了$i$步的方案数为$X[i]$，$y$维走了$j$步的方案数为$Y[j]$，两个维度一共走了$(i+j)$步，排列就是$(i+j)!$，但是这些步的顺序在每个维度内是固定的，所以还要除以$i！$和$j！$

好！现在求出来了到$(n,m,w)$的方案数，那么最后答案就是 [(1,1,1)到(n,m,w)的方案数] -[(1,1,1)到(R1,C1,H1)的方案数] - [(1,1,1)到(R2,C2,H2)的方案数]+[(R1,C1,H1)到(R2,C2,H2)的方案数] 。简单的容斥一下就好了。

这样我们就合并了两个维度，那么再合并一个维度就跟上面的原理是一样的了。

AC_Code

#include 
using namespace std;
#define mod 1000000007
const int N = 2020;
typedef long long ll;
ll vis[N], prime[N];
ll jie[N],S[N][N];
ll tot;
ll inv(ll x){
	ll p=mod-2;
	ll y=1;
	while(p){
		if(p&1){
			y=(y*x)%mod;
		}
		x=(x*x)%mod;
		p>>=1;
	}
	return y;
}

ll dp[N][N];
void preparation(ll n,ll m,ll w){
	if(n<1||m<1||w<1)return ;
	int nm=max(n+m,w);
	jie[0]=1;
	for(int i=1;i<=nm;i++)jie[i]=(jie[i-1]*i)%mod;
	for(int i=0;i<=nm;i++){
		for(ll j=0;j<=i;j++){
			S[i][j]=((jie[i+j]*inv(jie[i]))%mod*inv(jie[j]))%mod;
			S[j][i]=S[i][j];
		}
	}
	int mm=max(max(n,m),w);
	for(int i=2;i<=mm;i++){
		if(!vis[i])prime[++tot]=i;
		for(ll j=1;prime[j]*i<=mm&&j<=tot;j++){
			vis[prime[j]*i]=1;
		}
	}dp[1][0]=1;
	for(int i=2;i<=mm;i++){
		for(int k=1;k<=(i-1)/2;k++){
			for(int j=1;j<=tot&&prime[j]<i;j++){
				dp[i][k]=(dp[i][k]+dp[i-prime[j]][k-1])%mod;
			}
		}
	}
}
ll X[N],Y[N],Z[N],XY[N*2],XYZ[N*3];
ll find(ll x,ll y,ll z){
	ll totx=(x-1)/2,toty=(y-1)/2,totz=(z-1)/2,ans=0;
	for(int i=0;i<=totx;i++){
		X[i]=dp[x][i];
	}
	for(int i=0;i<=toty;i++){
		Y[i]=dp[y][i];

	}
	for(int i=0;i<=totz;i++){
		Z[i]=dp[z][i];
	}
	for(int i=0;i<=totx+toty;i++)XY[i]=0;
	for(int i=0;i<=totx;i++){
		for(int j=0;j<=toty;j++){
			XY[i+j]+=((X[i]*Y[j])%mod*S[i][j])%mod;
			XY[i+j]=XY[i+j]%mod;
		}
	}
	for(int i=0;i<=totx+toty+totz;i++)XYZ[i]=0;
	for(int i=0;i<=totx+toty;i++){
		for(ll j=0;j<=totz;j++){
			XYZ[i+j]+=(((XY[i]*Z[j])%mod)*S[i][j])%mod;
			XYZ[i+j]=XYZ[i+j]%mod;
		}
	}
	for(ll i=0;i<=totx+toty+totz;i++)ans=(ans+XYZ[i])%mod;
	return ans;
}
ll n,m,w,R1,R2,C1,C2,H1,H2;
int main(){
	scanf("%lld%lld%lld",&n,&m,&w);
	scanf("%lld%lld%lld%lld%lld%lld",&R1,&C1,&H1,&R2,&C2,&H2);
	if(R1>R2||C1>C2||H1>H2){
		swap(R1,R2);swap(C1,C2);swap(H1,H2);
	}
	preparation(n,m,w);
	ll ans1=find(n,m,w);
	ll ans2=(find(R1,C1,H1)*find(n-R1+1,m-C1+1,w-H1+1))%mod;
	ll ans3=(find(R2,C2,H2)*find(n-R2+1,m-C2+1,w-H2+1))%mod;
	ll ans4=(((find(R1,C1,H1)*find(R2-R1+1,C2-C1+1,H2-H1+1))%mod)*find(n-R2+1,m-C2+1,w-H2+1))%mod;
	printf("%lld\n",(((ans1-ans2 + mod) % mod-ans3 + mod) % mod+ans4+mod)%mod);
}