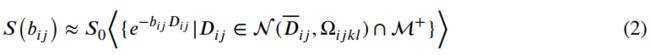人脑体内扩散张量分布MRI的新框架
导读
神经组织微观结构在发育、生理和病理生理过程中起着重要作用。扩散张量分布(DTD)MRI利用扩散张量的概率密度函数为特征的非交换隔室集合来描述体素内的水扩散,从而有助于探测亚体素的异质性。本文提供了一个新的框架,用于在活体人脑中获取多个扩散编码(MDE)图像并从中估计DTD。本研究在单个自旋回波中融合了脉冲场梯度(iPFG),以生成任意的1、2或3阶b张量,而不会伴随梯度伪影。采用明确定义的扩散编码参数,本文表明iPFG保留了传统多个PFG(mPFG/MDE)序列的显著特征,同时减少了回波时间和相干路径伪影,从而将其应用扩展到DTD MRI之外。该DTD是一个最大熵张量变量正态分布,其张量随机变量被约束为正定性以确保其物理性质。在每个体素中,使用蒙特卡罗方法估计DTD的二阶均值和四阶协方差张量,该方法合成具有相应大小、形状和方向分布的微扩散张量,以最佳拟合测量的MDE图像。从这些张量中,可以获得扩散张量椭球大小和形状的光谱,以及解开体素内潜在异质性的微观取向分布函数(μODF)和微观分数各向异性(μFA)。使用DTD衍生的μODF,本文介绍了一种执行纤维束成像的新方法,该方法能够处理复杂的纤维结构。结果揭示了以前未观察到的各种灰质和白质区域的微观各向异性以及小脑灰质中的偏态MD分布。DTD MRI纤维束成像捕获了与已知解剖结构一致的复杂白质纤维组织。DTD MRI还解决了一些与扩散张量成像(DTI)相关的简并现象,并阐明了扩散异质性的来源,这可能有助于提高各种神经系统疾病和障碍的诊断。
前言
非侵入性地测量和绘制神经组织微观结构一直是神经科学领域长期追求的目标。在过去的几十年里,MRI技术的重大进步,包括并行成像重建、硬件和脉冲序列的改进等,都有助于实现毫米级体素分辨率。然而,即使在这个长度尺度上,神经组织仍然由高度异质和各向异性的微域组成,尽管在传统的标量值MRI中其外观是一致的。扩散张量成像(DTI)能够通过探测体素内水分子的扩散来解析远小于体素尺寸的微米尺度特征,例如Basser等人(1994a,b)使用从单脉冲场梯度(sPFG)实验估计的二阶扩散张量建模来探测水分子在体素模型中的扩散。结果表明,Stejskal-Tanner实验中的标量扩散加权因子(即b值)需要用矩阵或张量(即b张量)代替,以表征组织的各向异性。然而,DTI仅提供在整个MRI体素上平均的平均扩散张量,这掩盖了神经组织的潜在异质性。虽然其中一些限制可以通过提高空间分辨率来克服,但这是以降低信噪比(SNR)和增加扫描时间为代价的。MRI的基本SNR限制使其无法分辨大小在0.1-60μm之间的单个神经元胞体和轴突。
多个脉冲场梯度(mPFG)或多个扩散编码(MDE)实验已被证明可以通过区分宏观和微观尺度的各向异性来消除与DTI相关的一些简并现象。这再次激发了扩散MRI社区对阐明DTI以外的神经组织微观结构的兴趣。然而,其中许多方法通常依赖于对材料微观结构或形态的假设,例如,材料由球形或椭圆形孔组成,限制了它们对复杂神经组织的适用性,尤其是在微观结构变化未知的病理组织中。
在电子显微图像中观察到的神经组织微观结构的一个更普遍的特征是由大小、形状和方向各异的充满水的隔室组成,每个隔室都被一层质膜包围。尽管这些单独隔室的原始MR成像的SNR令人望而却步,但在每个体素内映射整体的统计特性是可行的,并且可以提供在疾病期间发生的亚体素尺度的微观结构变化的敏感测量。鉴于水在质膜上通过脂质双分子层、水孔蛋白和转运蛋白的渗透性,每个隔室内的水扩散可以建模为由单个二阶扩散张量描述的受阻高斯扩散过程。假设宏观MRI体素在扩散实验的时间尺度上是由一个连续的非交换微域或微体素组成,Basser和Pajevic(2003)提出了扩散张量空间中的概率密度函数,也称为扩散张量分布(DTD),可以描述这种微结构。Jian等人(2007)提出的MR信号模型是由微体素引起的高斯扩散信号衰减曲线的线性叠加。尽管他们使用了sPFG数据,但后来认识到需要mPFG数据才能明确地估计完整的DTD。
估计DTD被证明是一个不适定的逆问题,因为它需要对测量的扩散加权图像(DWIs)进行拉普拉斯逆变换。文献中提出了几种方法来克服这种不适定性,包括使用参数分布,通过扩展基于累积量的MR信号来部分重建非参数分布,以及对微扩散张量的方向和对称性施加约束。本研究使用的DTD是正态张量变量分布(NTVD),其样本被约束为正定分布(CNTVD),以确保其物理性质。研究者之前证明了CNTVD具有一些有用的性质,例如最大熵、紧凑性,并且仅需要一阶和二阶b张量进行估计,这克服了以往方法的一些局限性。
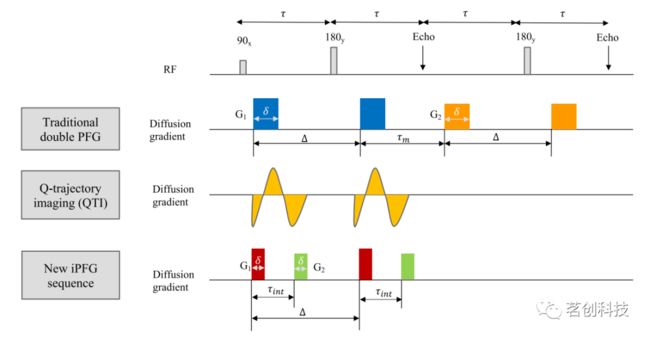
在给定DTD估计的理论框架下,由于连续应用多个梯度对导致的长回波时间(TE),以及多个重聚焦射频(RF)脉冲产生的相干伪影,因而实施mPFG MRI实验具有挑战性。使用脉冲场梯度的组合引入了几个mPFG的单自旋回波变体,但这些方法可能很麻烦,因为改变b-张量的形状需要使用不同的梯度集,并且可能会受到偏置DTD测量所带来的梯度伪影的影响。最近,mPFG的一种单自旋回波变体涉及使用自由优化的梯度波形来生成任意阶的b张量,称为q轨迹成像(QTI)。尽管QTI具有通用性,但同时也具有局限性,例如缺乏明确定义的扩散时间和扩散脉冲持续时间,这限制了对测量信号的物理解释。形状复杂的梯度波形可能难以调试/实现。尽管具有时效性,但180°RF脉冲周围扩散梯度的不对称性引入了伴随的梯度伪影。这可以通过对称化180°脉冲周围的扩散梯度(该方法增加了TE),或者通过在梯度形状优化程序中添加约束(增加了其复杂性)来部分克服。
本研究介绍了一种新的通用的、易于实现的mPFG MRI实验,该实验使用单个自旋回波而不会伴随梯度伪影,能够使用融合梯度脉冲生成任意一阶、二阶或三阶的b张量。本研究的脉冲序列具有明确定义的扩散梯度、脉冲宽度和扩散时间,因此可以使用q空间形式对DTD MRI以外的应用进行分析和解释。本文使用了研究者之前提出的基于压缩感知(CS)的优化实验设计来均匀采样b张量,其椭球具有不同的大小、形状和方向,与现有方案相比,其偏差可能更小。本研究使用新的标量测量来解开体素内组织的大小、形状和方向异质性,并提出一种新方法来执行纤维束成像,从而自然地解释复杂的纤维结构。本研究结果表明,衍生的异质性测量和DTD纤维束成像能够捕获活体人脑组织中已建立的微结构特征并揭示新的特征。
材料和方法
信号模型
来自DTD的MR信号p(Dij)由下式得到:
其中S0为无扩散加权的信号,M+为正定扩散张量空间,bij、Dij分别为二阶b张量和扩散张量。假设CNTVD为p(Dij),则对样本Dij进行蒙特卡罗(MC)积分来近似信号方程,样本Dij来自一个给定二阶均值Dij和四阶协方差张量Ωijkl的NTVD,这些样本经过如下滤波以确保集合的正定性:
其中尖括号表示对所有微扩散张量的集平均,N是NTVD。为了方便起见,在从分布中抽取样本时,将N的均值和协方差张量分别表示为一个6D向量和6×6对称正定矩阵。
MRI脉冲序列与实验设计
与传统方法和QTI方法相比,用于生成一阶和二阶b张量的新dPFG脉冲序列如图1所示。将两个被任意时间延迟(即融合时间)隔开的独立扩散梯度脉冲合并到单个自旋回波序列中,称之为融合-PFG(iPFG),以减少与传统dPFG序列相比的TE。与QTI序列相比,使用PFGs而不是自由波形更容易实现和调试。本研究脉冲序列设计使用波形对称策略来消除伴随的梯度伪影,这种伪影会随着梯度强度和样本维数的增加而恶化,尤其不利于扩散成像。如图1所示,通过在180°RF脉冲的两侧对称地拆分两个梯度对来去除伴随的梯度伪影。应该注意的是,扩展iPFG编码以生成三阶b张量将需要一个额外的独立梯度脉冲。
图1.与传统方法和最近的q轨迹成像(QTI)相比,新的融合脉冲场梯度(iPFG)能够在用于估计DTD的单个自旋回波中生成任意形状的一阶和二阶b张量。
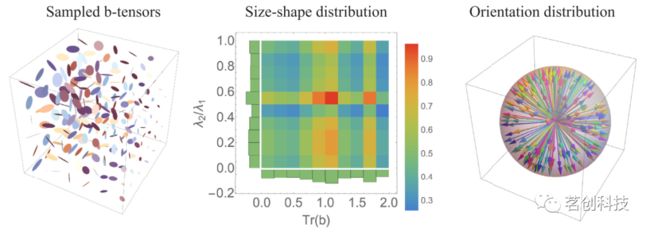
Magdoom等人(2021)描述的基于压缩感知的实验设计用于生成一组一阶和二阶b张量。简而言之,b张量的特征向量被随机旋转到均匀的样本方向,同时对它们的两个非零特征值进行约束,使它们的和与比值分别在大小和形状上服从均匀分布。在梯度持续时间(δ)、融合时间(τint)和扩散时间(∆)固定的条件下,通过MATLAB(Mathworks、Natick、MA)数值优化得到新脉冲序列中的扩散梯度向量。
MRI测量和预处理
使用20通道射频线圈在3T扫描仪(Prisma,Siemens Healthineers)上采集MRI数据,该扫描仪的梯度强度高达80mT/m,转换速率可达200T/m/s,采用回波平面成像(EPI)读取。根据美国国立神经疾病和卒中研究所(NINDS)内部研究计划的机构审查委员会(IRB)批准的研究方案提供知情同意,本研究对24岁和47岁的健康男性志愿者进行了测量。为了测试DTD估计管道的可重复性,其中一名志愿者在单独的成像会话中被扫描了两次。相关采集参数如下:δ\τint\∆=14\14\40ms,TR\TE=3500\90ms,视场(FOV)=210mm×210mm×150mm,1490Hz/pixel带宽下的平面空间分辨率为1.5mm,5mm层厚,GRAPPA加速因子=3,部分傅里叶因子=6/8。如图2所示,共采集了216个大小、形状和方向一致的不同b张量,b值范围为0-2000s/mm2。以反相编码方向重复b=0s/mm2采集,以校正磁化率引起的几何失真。
图2
在DTD重建之前,对单个DWI进行以下顺序的处理:1)在DIPY软件环境中使用Marchenko-Pastur主成分分析(MP-PCA)算法抑制随机噪声;2)在FSL软件环境下使用3D仿射变换将采集到的DWIs与b=0s/mm2配准,以减少扫描间主体运动和涡流引起的几何失真;3)在FSL软件环境中使用基于反相位编码数据估计出的偏共振磁场,以计算静态场的非均匀性引起的几何失真。
微结构测量和纤维束成像的估计
CNTVD的均值和协方差张量是根据Magdoom等人(2021)所概述的DWIs方法来进行估计的。简而言之,利用均值和协方差张量的不同对称性来构建一组嵌套模型,使用贝叶斯信息准则(BIC)从中选择最简约、最能解释信号的模型。对于给定的嵌套模型,使用单纯形数值优化算法估计未知参数,拟合出等式(2)中的MR信号。本研究使用Cholesky分解对均值和协方差张量施加正定性约束,从而改进了本研究的估计管道。
估计的CNTVD参数用于描绘体素内的几个微结构特征,正如Magdoom等人(2021)所述。简而言之,通过从CNTVD中抽取MC样本以及估计的均值和协方差张量来模拟体素中的微扩散张量。宏观分数各向异性(FA)和宏观取向分布函数(ODF)由平均扩散张量计算,而微观FA和微观ODF(分别为μFA和μODF)由各微观扩散张量上的FA和ODF的集平均计算。由于相关算子(例如FA、ODF等)的不可交换性,“宏观”和“微观”的量通常不相等。
根据微扩散张量椭球的大小、形状和方向异质性对组织的异质性进行分类。微扩散张量的大小和形状分别由扩散张量的三分之一迹(即平均扩散率,MD)和FA加权特征值偏度来量化,并对其分布进行测量和映射。方向异质性Vorient测量微扩散张量的方向离散程度。使用宏观和微观ODF对全脑进行纤维束成像。为了更好地描绘ODF峰,在执行纤维束成像之前,使用在DIPY软件中的反卷积变换对ODF进行滤波/锐化。使用μFA图生成白质掩膜,并在MRTrix软件环境中使用滤波后的宏观和微观ODF执行流线纤维束成像。
结果
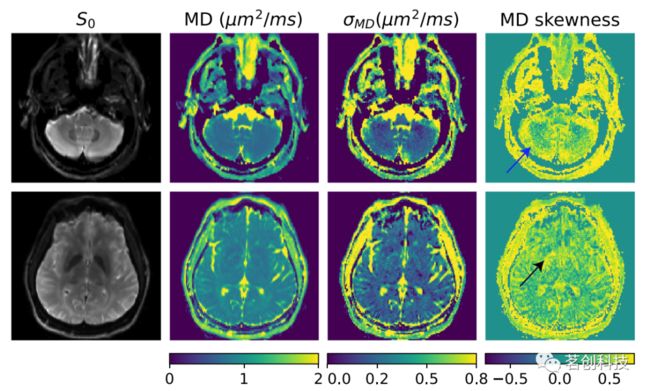
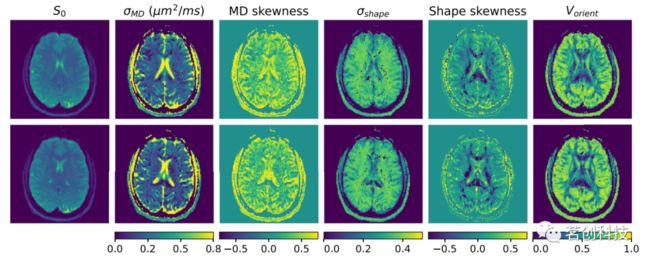
除胼胝体内的区域外,大部分中枢神经系统(CNS)均存在不同程度的异质性和微观各向异性。通过平均扩散率(MD)分布的矩来量化CNS的异质性,如图3所示。除CSF污染的体素外,脑实质中的均值是一致的,而偏度等较高的矩显示平均值中不存在新的对比度。特别是,与周围环境相比,小脑和皮层下灰质的偏度大约提高了两倍,如图中分别使用蓝色和黑色箭头突出显示。在脑脊液(CSF)充盈区域,与脑室-组织边界处的偏度(≈0.9)相比,脑室内的偏度(≈0.4)较低,而标准差均匀且升高。
图3
由形状测量的矩给出的CNS中的形状异质性如图4所示。与灰质和复杂纤维区域相比,相干白质区域的微扩散张量的平均形状测量值总体为正。与CSF充盈区域(≈0.2)相比,脑实质区的标准差较高(≈0.4)。相干白质的偏度总体为负,而在其他区域为正。
图4
μFA和Vorient测量描述的CNS中的方向异质性如图5所示,并提供了平均扩散张量的FA和颜色编码的FA加权主特征向量以供参考。基于DTI的FA和DEC图显示白质束的方向结构与既往研究结果一致。μFA在高度相干的白质束和CSF充盈区域中近似等于FA,而在灰质和白质内的复杂纤维区域中升高,例如在图中使用黑色箭头显示的放射冠中。Vorient测量值与白质中的FA成反比。它们的值在大脑皮层和小脑灰质中升高,如下图中分别使用红色和蓝色箭头显示的这些区域中观察到的μFA增加。
图5
除了提供新的对比度外,DTD MRI还有助于解决与DTI相关的混淆问题。例如,在放射冠中观察到的FA减少(图5中的黑色箭头)可能是疾病中发生的水肿的结果,或者是由于方向或形状异质性引起的微观各向异性。DTD MRI测量表明该区域的主要异质性是由形状引起的,因为σMD和Vorient都很小,有助于消除这种模糊性。因此,该区域的FA减少不是由于水肿,因为它会导致σMD增加,而是由于该区域的高度形状异质性,这可能是由于纤维在亚微体素尺度上的伸展。
DTD测量的可重复性是通过比较在大致相同切片位置的不同成像会话中对同一被试扫描两次所获得的结果来证明的,如图6所示。结果还包括对灰质、白质和CSF部分的感兴趣区域(ROIs)的DTD测量进行定量比较,如表1所示。可以观察到,在两次重复中都再现了测量的几个空间特征。这包括在CSF填充区域观察到的σMD增加,脑室内MD偏度降低,实质中均匀的σshape和相干白质中的负形状偏度,相干白质中的Vorient减少,以及大脑皮层中的Vorient增加。应该注意的是,重复测量之间也存在一些差异,例如白质中的MD偏度值和CSF中的形状偏度值,这可能是由于较高光谱矩对噪声的敏感性增加所致。
表1
图6
通过比较图7所示的几个ROI中的宏观和微观ODFs,可以看到脑组织的方向离散度。在胼胝体、放射冠和内囊纤维中选择ROI。在胼胝体ROI中,宏观和微观ODFs是相同的。在放射冠ROI中,宏观ODFs显示单个纤维群,而μODFs清楚地显示两个纤维群的粘连或交叉。在内囊ROI中,宏观ODFs反映了两个具有独特主要方向的纤维群,在DEC图中以不同的颜色显示。然而,μODFs清楚地显示了两个纤维群之间几乎呈90度的交叉,尤其是在交界处。
图7
使用滤波后的宏观和微观ODFs对全脑执行流线纤维束成像的结果如图8所示。正如预期的那样,DTI纤维束成像能准确地重建胼胝体等相干白质区域的纤维。然而,由于本研究中采用的层厚较大,它未能捕获体素内存在的垂直纤维束,如箭头所示,这是由μODF解释的。在其他一些具有复杂纤维结构的白质区域也观察到DTI束和DTD束之间的差异。胼胝体纤维向大脑皮层多个区域的投影在DTI纤维束成像中缺失,而在DTD纤维束成像中清晰可见。
图8
结论
本研究提出了一套新的工具来测量和映射活体人脑中的DTD,引入了一种在单个自旋回波序列中执行mPFG MRI实验的新方法,该序列能够生成一阶、二阶或三阶的b张量,而不会伴随梯度伪影。本研究证实了该实验设计和信号反转框架能够捕获神经组织的异质性。然而,蒙特卡罗方法的局限性之一是计算时间长,未来可以通过使用图形处理单元(GPU)执行模型拟合来克服这一问题。需要注意的是,即使在本研究中使用的空间分辨率和扩散梯度下,宏观异质性也可能在某些体素中占主导地位,尤其是那些具有CSF的体素。随着高级图像读出策略和更强梯度的出现,通过在高k空间和q空间分辨率下执行DTD,有可能在更大比例的体素中实现真正的介观分辨率。这将有助于推进新的异质性测量和纤维束成像在评估新疾病、正常和异常发育过程、大脑和其他软组织退化和创伤中的应用。
原文:Kulam Najmudeen Magdoom, Alexandru V. Avram, Joelle E. Sarlls, Gasbarra Dario, Peter J. Basser, A Novel Framework for In-vivo Diffusion Tensor Distribution MRI of the Human Brain, NeuroImage (2023), doi: https://doi.org/10.1016/j.neuroimage.2023.120003