The 2020 ICPC Asia Taipei-Hsinchu Site Programming Contest--C.Pyramid

Problem Description

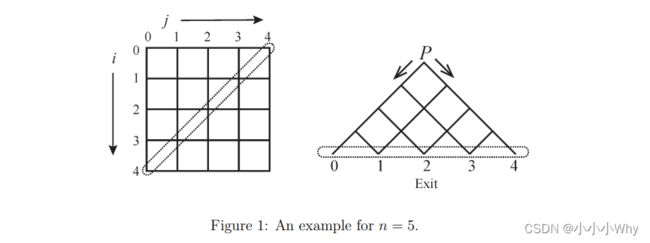
Consider an × grid where nodes are labelled as (, ) for 0 ≤ , < . We rotate it 45 degree in clockwise direction and keep only its top half part. Then you get a pyramid, as shown in Figure 1. All of the nodes laid on the anti-diagonal of the grid have labels ( − 1 − , ) for 0 ≤ < . They are located at the bottom line of the pyramid. For simplicity and clarity, we name node ( − 1 − , ) as exit . Node (0, 0) is called the starting point (labelled as in Figure 1). When you insert a ball from the starting point, this ball will roll down to some of the exits. A ball located at node (, ) can only roll down to either node ( + 1, ) or node (, + 1), and the ball shall never be broken or split. There is a tiny switch equipped on every node other than the exits that controls the move direction of the ball, and this switch always works well. The switch has exactly two states: either or , indicates that the ball can move to node ( + 1, ) or (, + 1), respectively. After the ball leaves this node, the switch changes immediately to the other state. The default setting for a switch is at .

 When you insert the first ball into , this ball will reach exit 0, and the states of nodes (, 0) for 0 ≤ < − 1 are now all ’s. Then you insert the second, third, and so on so forth, one by one, until the ℎ ball finishes. The status of every switch accumulates with these balls. Please write a program to determine the number of the exit point for the ℎ ball.

Input Format

The first line of the input is a number that specifies the number of test cases. Each test case has only one line that gives you two space-delimited numbers and .

Output Format

Please output the exit number of the ℎ ball in one line.

Technical Specification

• There are at most 20 test cases.

• 1 ≤ ≤ 10^4 . • 1 ≤ ≤ 10^8

Input

3
5 3
5 4
5 5

Output

2
3
2

题意：刚开始每个节点都是关闭的，放球，如果该节点是关闭的，那么会向左下走，否则右下走，然后改变节点的状态(开关)，问你第k个球最后落在哪个下标(从0开始)。

解析：我们可以求出前k-1的球落完之后的状态，那么模拟最后一个球就很容易了，需要知道对于一个节点，如果有m个球经过，那么有去往左边，有去往右边，那么我们最开始让k-1个球从起点落下跑一边就可以得到k-1的球导致的状态。

虽然可以进行优化，但是这种方法好理解

#include 
const int N=10005;
int a[N][N];
void solve()
{
	int n,k;
	scanf("%d%d",&n,&k);
	a[0][0]=--k;//前k-1个球
	for(int i=0;i