[文献翻译自用]运用本地差分隐私的基于物品的协同过滤

Differentially Private Collaborative Coupling Learning for Recommender Systems（Yanjun Zhang）

(IEEE Intelligent System(2021))

运用本地差分隐私的基于物品的协同过滤

Abstract

近年来，基于项目的协同过滤引起了广泛的关注。它根据用户报告的历史数据 (即他们已经感兴趣的商品)，向用户推荐他们可能感兴趣的新商品。如果服务器不能被完全信任，则所报告的历史数据会带来重大的隐私风险。许多研究集中于开发差分隐私保护机制来保护个人数据。然而，这些机制大多不能确保推荐的准确性。主要是因为这些方法直接利用扰动数据计算相似度。因此，计算的相似度总是不准确的，这种不准确的相似度会导致推荐结果的不准确。本文提出了一种本地差异隐私的基于物品的协同过滤框架，该框架在用户端保护用户的私有历史数据，在服务器端重构相似度以保证推荐的准确性。通过估计没有对任何一项、一项或两项都评级的用户数量，可以重建每对项目的相似度。最终推荐结果由重构的相似度得出。实验结果表明，我们提出的方法在推荐准确度以及隐私保护和准确度之间的权衡方面明显优于现有方法。

1.Introduction

网络技术的快速发展产生了大量的网络信息。如何快速准确地找到目标用户可能感兴趣的信息已经成为一个难题。基于物品的协同过滤是解决这一问题的有效途径，广泛应用于其他领域，如 loT 环境[21]，智慧城市[44]。该方法分析物品之间的相似性，然后根据相似性确定推荐的项目集[5]。

然而，推荐算法的应用带来了用户的隐私问题，因为它要求每个用户提供他们的历史数据 (例如，他看的电影、他阅读的材料等)。这些隐私问题将影响用户提供数据的意愿，导致推荐结果的准确性低[3，41]。因此，隐私保护推荐技术越来越受到学术界的关注。保护用户隐私的一个直接的方法是通过添加一些噪音来干扰历史数据 [27.28]。实现这种保护有多种方式(见[6])。很难评估这些隐私保护方法，因为缺少严格的理论基础去权衡隐私保护效果和推荐系统的准确性。

差异隐私(DP) [9]是一个严格的隐私概念，这个概念权衡着隐私保护和数据效用。因此，它也被用于推荐领域，以保护本地环境中用户历史数据的隐私[ 14，34，35]。本地环境中的差分隐私推荐包括两个主要阶段:(1)客户端干扰用户的历史数据，以及(2)服务器执行相似度计算并做出推荐。扰动的数据将导致用于推荐的数据和项目之间的相似性得分不准确，这又会导致推荐准确性差。

本文的动机是，如果我们能够重建原始数据与原始数据的相似度公式，那么我们就可以大大提高在本地环境下差异私人推荐的准确性。其动机类似于局部差异隐私 (LDP)的思想[ 15，20]。LDP 是一个数据收集框架，其主要思想是确保数据收集折不能收集任何个人数据的精确值，但仍然可以重建原始数据的统计特性，例如计数[10]、直方图[1]和每个属性的平均值[8]。然而，现有的 LDP 机制不能直接重构推荐中的相似度得分，相似度计算不仅需要重构每一项的统计特性，还需要重构任意两项之间的相关性。为了解决这个问题，我们将相似性得分的问题分解为两部分，一部分是估计历史数据中涉及的每个项目的数量(频数估计)，另一部分是每两个项目在历史数据中被同时提到的数量（联合频数估计)。

本文的主要贡献在于，据我们所知，我们是第一个提出基于差分隐私的协同过滤中相似度得分需要重构的。在真实数据集上的实验结果表明，相似度重构可以极大地提高推荐的准确性，并在隐私和准确性之间取得平衡。

本文的其余部分组织如下。第二部分总结了相关工作。第 3 节正式定义了基于局部差分隐私的协作过滤问题。第 4 节详细介绍了提出的方法。第五部分介绍了实验结果。最后，我们在第 6 节结束了这项工作。

2.Ralated work

本文涉及本地环境下的差分隐私推荐和本地差分隐私下的频数估计。

2.1本地差分隐私

一些研究旨在通过使用差分隐私机制在用户端保护用户的历史评分。刘等[24]设计了一种混合方法，通过将差分隐私和随机扰动相结合来保护推荐系统的隐私。首先，为了防止用户的个人数据被不可信的推荐系统收集，他们通过使用随机扰动技术给用户端的用户评分增加了噪声。然后，为了防止攻击者根据推荐结果推断任何单个用户的数据，他们在计算物品之间的关系时加入了不同的私人噪声。这种方法可以提供更多的隐私保护，但也会导致准确性损失。为了解决这个问题，孟等人[25]认为只有部分用户的历史评分是敏感的。基于这一假设，他们将用户的历史评分分为敏感和非敏感评分，并在敏感的历史评分上增加了较大的幅度噪声。因此，敏感评级可以得到更好的隐私保护，而非敏感评级可以获得更好的推荐准确性。

但有研究表明用户更关心历史数据而不是评分数据[47.48]。基于这一结论，最近的一些研究集中在不可信服务器环境下保护用户的历史数据。Shen 等人[34]提出了一种在不可信服务器环境下保护隐私的用户扰动框架。在这个框架内。扰动数据的类别聚合无论是否存在单个项目都满足差异隐私。在此基础上，他们为个性化推荐系统提出了第一个实用的增强隐私的内置客户端，在用户端执行数据扰动以保护用户的隐私。这两项工作要求用户将他们历史数据的类别集合发送到服务器端。然而，大多数现有的 web 应用程序要求用户发送他们的历史数据，而不是类别集合。为了解决这个问题，Guerraoui 等人[14]提出了一种基于距离的差分隐私协议，其使用概率替代技术来基于距离阈值(λ)创建原始用户简档的模仿简档。但是，它假设用户对所有项目都有相同的隐私偏好。【没有考虑不同用户的隐私偏好】来解决这个问题。Li 等人[23]提出了一种基于局部聚类的个性化差别隐私方案，用于基于隐私保护的用户协作过滤推荐器，其中每个用户可以独立地为他们的个人数据指定隐私设置。Zhang 等[43]他设计了一个微分私有矩阵分解模型，该模型是通过目标扰动方法实现的。姜等人在[18]提出了一种隐私保护的分布式推荐框架。该框架通过使用两种随机响应算法，在用户-服务器环境下以安全的方式计算未评级项目的矩阵分解梯度。Shin H.等[36]提出了一个差分隐私矩阵分解框架，它保护用户的项目和评分。在这个框架中，隐私通过两个步骤得到保护。首先，用户随机分配他们的数据以满足差分要求，并将被扰乱的数据发送给推荐服务器。然后，推荐服务器在每个用户每次梯度下降迭代的过程中所有梯度提供差分隐私保护。Boutet[2]提出了一种隐私保护的分布式协作机制，保护用户的个人资料不被其他未授权的用户访问。所提出的机制依赖于一个原始的混淆方案和一个基于随机的传播协议。前者隐藏了用户的确切概况，而没有显著降低他们推荐的效用；后者确保了传播过程中的不同隐私。Li 等[22]提出了一种隐私保护的共享协同过滤方法。首先，采用基于本地敏感度的差分隐私框架来促进每个用户的隐私实施，然后开发两种基于项目的邻域提升算法来做出高质量的推荐。

2.2本地差分隐私的频数估计

本地差分隐私(LDP) [15,20]是一个数据收集框架。该框架主要包括两个部分: 首先，每个用户在本地扰动他的数据以满足 ε-differential 隐私，然后将扰动后的数据发送给聚合器；第二，数据聚合器根据扰动数据和数据扰动方法学习原始数据的统计特性。整合的最基本的目标是频数估计。Erlingsson等人[10]提出了一种用于本地差分保护和统计众包的数据收集的通用技术。在此基础上，他们进一步提出了一种隐私保护的可聚集随机反应机制，即 RAPPOR。具体来说，假设用户需要向数据采集器发送 d 位数据，RAPPOR 采用随机响应(RR)机制来独立扰动每一位数据。RAPPOR 的一个缺点是它的高通信开销。为了解决这个问题，Bassily 等人[1]提出了一种简洁的直方图(SH)机制，该机制基于这样一种思想，即每个用户只报告 SH 中的一个随机选择的位，而不报告 RAPPOR 中的 d 位。然而，这种方法仅限于简单的数字或分类属性，不适用于更复杂类型的数据挖掘任务。Qin等[25]提出了一种在局部差分隐私保护条件下挖掘重磅炸弹的算法，称为 LDPMiner。LDPMiner 包括两个阶段:第一，使用隐私预算部分为前 k 个频繁项确定候选集；第二，将剩余的隐私预算集中于细化候选集。Wang 等人[39]分析了现有的 LDP 技术的特性，并定义如果 LDP 协议产生无偏估计，则该协议是“纯”的。基于此，他们提出了一个“纯”LDP 协议框架，并引入了一种通用的聚合和解码技术，适用于所有“纯”LDP 协议。
上述方法生成并报告伪装的数据，只能重构各数据的统计特征，不能重构数据间的互相关性。为了解决这个问题，Set等[43]提出了S2M和S2Mb，两者都在用户端根据用户的个人数据生成一组伪装数据，然后在服务器端重建交叉制表。具体来说，假设有 g 个属性，表示为$A_1,A_2,...A_g$。然后，S2M 和 S2 将这些属性$A_1\ast A_2\ast ...\ast A_g$合并为一个带有ID域的属性。并在ID域执行匿名化算法和重构算法。ID 域的大小呈指数级增长。因此，S2M 和 S2Mb 仅适用于数据空间相对较小的情况。最近的一些研究考虑了在本地差分隐私下发布边际表的问题。例如[4，31]这些方法可以用来分析多个数据之间的相关性，但是当属性的数量增多时，它们的性能就很差。为了解决这个问题，张等人 a1[45]提出了一个 LDP协议来构建高维属性的边际。它首先生成一些边际表，然后干扰边际表，并将有噪声的边际表发送到服务器端。然而，这种方法不适用于基于项目的协作过滤，因为它需要用户报告他们的历史数据，而不是边际表。

总之，已有的本地差分隐私推荐方法常常导致推荐精度下降，因为它们没有分析已被扰动的数据来消除由随机化引起的误差。现有的 LDP 机制可以估计原始数据的统计特性，但是，它们大多侧重于依赖频数估计的更复杂的问题，例如heavy hitter identification和频繁项集挖掘。为了实现这些目标，他们通常首先确定一个候选集，然后专注于细化候选集。因此，它们的目标不同于基于物品的协作过滤，后者要求对所有项目做出良好的估计。此外，对于任何两个物品，现有的 LDP 机制可以回答有多少用户拥有其中一个项目，但不能回答有多少用户同时拥有这两个项目。因此，现有的 LDP 机制无法分析项目之间的相关性，也无法估计项目之间的相似性得分，其结果是现有的 LDP 机制不适用于推荐场景。因此，有必要提出一种本地有差异的私人推荐机制：

• 在用户端干扰用户的历史数据以确保用户的数据隐私；
• 通过分析原始数据的统计特性和相关性来重建相似度得分，以确保高推荐精度。

3.Problem definition

在这一部分，我们对本文提及的问题作正式的定义。

3.1 无隐私保护的基于物品的协同过滤

近年来，对基于物品的协同过滤进行了大量的研究。他们中的大多数人都认为推荐包括收集用户的历史数据，计算项目之间的相关性，为目标用户计算项目的预测得分，并做出推荐[11.30]。本文从以下三个方面定义了本文使用的基于物品的协同过滤方法:
(1)相似度计算(2)预测得分计算(3)推荐方法。
首先，使用基于条件概率的经典相似度计算方法。
假定n个用户，$U=U_1,U_2,U_3...U_n$ ;m个物品,$I=I_1,I_2...I_m$; 任意用户的历史数据记为$X_u$，对于$U_u\in U$ 有$I_u\in I$; 下式定义$join{t}_{f}req()和freq()$函数:

两个物品之间的相似度公式如下：

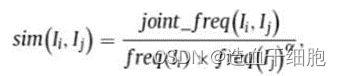
第二步，用加权和来计算用户$U_u$对于物品$I_u$的预测分数$p_u^i$。

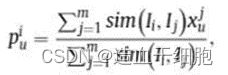
最后，给目标用户推荐评分位于前n的物品。

3.2 威胁模型

本文考虑的基于物品的协同过滤推荐由两个参与者组成:用户端和服务器端。根据[34.35]中介绍的威胁模型，我们假设用户端在用户的控制下，因此是可信的，而服务器端是半可信的。这里的“半可信”是指，服务器端一方面诚实地执行推荐算法并向用户返回推荐；另一方面可能向其他方披露用户的历史数据。

3.3 隐私定义

3.3.1差分隐私

差分隐私是一个严格的隐私概念。对每对相邻数据组$D$和$D^{’}$，一个隐私保护方法M如果满足下式，则满足ε-差分隐私要求：

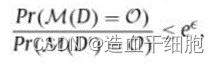
3.3.2本地差分隐私Local differential privacy LDP）

LDP是一种基于ε-差分隐私的数据收集框架。LDP的解由两部分组成:用户端数据扰动法和服务器端数据重构法[29]。
数据扰动法局部扰动用户的数据记录，以满足差异性隐私。形式上，对于任何两个数据记录 $X和X^{’}$，以及任何可能的输出 Y，a数据扰动机制 M 若满足下式则满足ε-差分隐私：

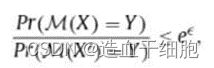
数据重构方法从用户那接收到的噪声数据中计算统计信息，以减少数据扰动方法造成的影响。

3.3.3 应用于基于物品的协同过滤时DP和LDP的局限性

DP 需要可信服务器，该服务器拥有一个包含多个用户确切数据记录的数据库，并通过向统计结果添加定制的噪声，通过向统计结果添加噪声来保护隐私数据。它不适用于本文所考虑的半可信服务器场景。

LDP 在不依赖可信服务器的情况下保证数据的隐私性；相反，每个用户扰乱自己的数据来满足差分隐私要求。请注意，LDP 定义中的数据$X和X^{’}$可以是任何两个单独的数据库，每个数据库只包含一条记录。这与DP 定义中的相邻数据集$D$ 和 $D^{’}$完全不同。但是，正如我们在第 3.1 节中所讨论的，用户的历史数据包含多个项目，因此，LDP 的隐私定义不适用于本文所考虑的情况。虽然使用合成定理[lS]可以多次扰动历史数据，正如我们将在第 4.2 节中讨论的，当历史数据的大小因用户而变化时，这种方法不能支持数据重建。

3.3.4 准确率定义

对于用户$U_u\in U$，不作隐私保护的推荐算法会把预测分数最高的前N个物品推荐给用户。而带隐私保护的推荐算法可能会推荐N个随机的物品给用户，导致原推荐算法预测效果的偏离。为了衡量这个偏离，我们定义了推荐准确性：

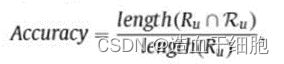
3.5问题声明

在做隐私推荐的时候不可避免的要平衡推荐效率和隐私保护效果。基于隐私维度和准确率维度，我们将局部差分隐私的基于物品的协作过滤问题形式化如下。

Definition 2 设计一个隐私保护的基于物品的协同过滤框架R，它

• 确保用户的个人数据对任何其他用户和服务器都是隐私的，即确保基于项目的协作过滤的ε-差分隐私；
• 在隐私和准确性之间进行合理的权衡。

一种隐私保护的协同过滤方法将导致较差的推荐准确性以及隐私和准确性之间的不良权衡，原因有二。首先，用于进行推荐的数据受到干扰。第二，由扰动数据计算的相似性分数是不准确的。为了保护用户的隐私，用于推荐的数据将不可避免地受到干扰。在接下来的章节中，我们将详细介绍我们提出的框架如何解决相似度评分不准确的问题，并最终提高推荐的准确性，并在隐私和准确性之间实现合理的平衡。

4.Method

在这一部分，我们将提出一个新颖的框架来实现基于物品的协同过滤算法的差分隐私保护。首先我们会介绍本框架的细节，然后展示已有的LDP并解释它为什么不能被用来在基于物品的协同过滤场景做数据重组。最后我们将分别展示我们的数据扰动方法和数据重组方法。

4.1 框架

如Fig 1所示，本文提出的本地差分隐私基于项目的协作过滤框架包含以下四个阶段。

• 数据扰动，客户端通过使用本地差分隐私机制来扰动用户的历史数据。
• 数据重建，服务器重构原始数据的统计特征。
• 相似度计算，服务器根据第二阶段重建的统计特征计算任意两个物品之间的相似度。
• 进行推荐，服务器根据在阶段 1 生成的被扰乱的历史数据和在阶段 3 计算的相似性得分向给定的目标用户推荐 N 个项目。

本文框架与现有的本地环境中差分推荐之间的主要区别在于阶段2。现有的方法直接计算扰动数据的统计性质，而我们的方法通过无偏估计方法重构原始数据的统计性质。

作为基于非私有项目的协作过滤，我们使用 Eq.(1) 计算任意两个项目之间的相似性得分，并使用Eq.(2)计算目标用户的项目预测得分。因此，本节仅详细介绍了数据扰动法和数据重构法。

4.2 已有方法

数据扰动和数据重建的直观解决方案是随机响应[7,40]。在这个模型中，聚合器询问每个用户他/她是否有敏感数据 A，用户使用随机机制来决定答案。随机机制的设计使得回答“是”和“否”的概率分别为 p 和 1-p。因此，聚合器可以按如下方式了解拥有敏感数据 a 的用户百分比。

基于随机响应技术，许多研究提出了大量的LDP协议。这些协议的目标有两个：一是每个用户能在用户端对自己的敏感信息进行扰动来满足ε-差分隐私的要求；另一个是聚合器可以重构用户原始信息的统计特征。Wang等[39]人定义了一个纯LDP协议的概念，如果这项协议支持无偏估计，则称它是纯（pure）的。因为‘pure’的LDP协议大多数源自直接编码(DE)或一元编码(UE)，所以本文只讨论这两种协议。

4.2.1 直接编码（Direct encoding）

直接编码(DE) [38]是二进制随机响应法的扩展，它适用于输入值多于2个的情况。假设有d个可能的值，并且用户$U_u$的原始数据是$X_u$，扰动方法定义如下。

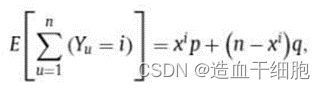
$x_i$为数值i的真实频数
假设对频率$（Y_u=i）$的期望值等于其统计值，则原始数据为i的用户数的无偏估计可计算如下:

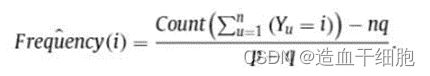
4.2.2 一元编码（Unary encoding）

当有d个可能取值时，与DE的假设一样，一元编码首先将d个可能取值编码为一个d元向量。$Encode(x)=[0,...,0,1,0,...0]$，其中对应用户值i的位置设置为1，其余为0
然后，对于每一位，UE的扰动方法将其以p和q的概率设置为1或0。计算方式如下：

最后计算初始值为i的频数：

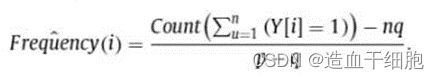
4.2.3 问题

DE和UE只能用于每个用户只有一个取值（只有一个物品评分？）的情况。然而，用户的历史信息在基于物品的协同过滤场景中会包含大量的元素。假设用户U_u 的历史数据有I_u项，确保历史数据满足差分隐私的直观方法可能是运行DE或UE $I_u$次。在每次运行中，该算法都以隐私预算$\epsilon /I_u$来扰动数据。我们认为在这种情况下，DE和UE都不能用于频数估计。这两种协议的证明是相似的，我们现在只证明当涉及多个项目时，DE 协议不能支持频率估计。
【若保证每个用户达到相同水平的隐私保护，每个用户的p和q值不尽相同，所以无法根据p\q恢复统计学特性】

4.3 数据扰动

上述的分析证明，当涉及多个物品时，需要满足两个条件：扰动算法需要pure；所有用户需要以相同的扰动概率来扰动他们的历史数据。从这两个条件出发，我们的数据扰动方法的基本思想是，如果我们把多个历史项目当作单个历史数据的一元编码，我们就可以以同样的概率扰动用户的历史数据。

假设有n个用户和m个物品，用户$U_u$的历史数据可以写作$X_u=[X_u^1$,$X_u^2$,…,$X_u^m$], $X_u^i$ $=1/0$表示用户$U_u$的历史数据中包不包含物品$I_i$。我们用$\overline{X_u^i}$来表示$X_u^i$取反的值。
数据扰动的目的是得到一个扰动历史数据集$Y_u=[Y_u^1,Y_u^2,\dots ,Y_u^m]$，（1）可以隐藏用户的真实历史数据。（2）保留一下历史数据用来实现推荐算法。为了实现这个目标，我们在涉及多个物品的情况使用了随机应答机制。具体来说，我们选取了一个概率参数p来表示扰动数据$Y_u^i$等于原始数据$X_u^i$的概率。显然，扰动数据$Y_u^i$等于$\overline{X_u^i}$的概率为1-p。

如上所述，p的值越大，数据的可用性越高。因此，对于p的选择控制这隐私保护与推荐准确性的平衡。然而，正如差分隐私定义中提到，这个平衡由参数ε控制。因此，选择p的同时也要满足差分隐私的要求。
Theorem1.当选择概率p位于$1/(e^{\epsilon }+1)$ 和 $e^{\epsilon }/(e^{\epsilon }+1)$之间，则该数据扰动方法满足ε差分隐私要求。【以下证明】

4.4数据重构

扰动的历史数据可能会带来不准确的相似度分数，进而导致推荐准确率的下降。为了解决这个问题，我们通过无偏估计的方法重构了相似度分数。和相似度计算的方法一样，为了重构相似度得分，我们需要估计在原始数据集中每一个物品出现的次数（频数估计）和在原始数据集中每两个物品同时出现的次数（联合频数估计）。

4.4.1 频数估计

X:用户初始的历史数据集，Y:扰动后的用户历史数据集。$x^i$和$y^i$分别表示物品$I^i$在X和Y中出现的次数。我们可以根据X计算出$y^i$的数学期望值：

$y^i$的值通过计算$y_u^i=1(u=1,2,...n)$的个数得到，另等式右边为$y^i$可以求出$x^i$。

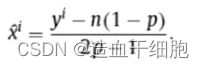
4.4.2 联合频数估计

另$x^{ij},y^{ij}$分别表示物品$I^i$和$I^j$在X和Y中同时出现的次数。和频数估计的推算一样，我们先根据X分析$y^{ij}$的数学期望值：

为了估计$x^{i}j$的值，我们还需要考虑物品$I^i$在但是$I^j$不在；$I^j$在但是$I^i$不在；$I^i$和$I^j$都不在的数学期望。

然后让这几个值都等于他们的期望，求出$x^{ij}$。

因此我们可以用频数估计求出的$x^i$和联合频数估计求出的$x^{ij}$来估计物品之间的相似度【取代开篇的$freq()$和$join{t}_{f}req()$】

4.5误差边界分析

我们现在为我们的数据重建方法计算给定隐私预算e的误差上限，该方法实现了恒定的估计精度。我们使用一个概率不等式(Hoeffding’s不等式)来给出误差界。在形式上，考虑一个正面概率为p，反面概率为1-p的硬币，如果我们掷 n 次硬币，硬币正面出现的预期次数是 pn。霍夫丁的不等式给出了偏离期望值超过一定量的概率的上限，定义如下。【期望值应该是n/2，会有所偏差，但是偏差值也有个范围】

4.5.1估计精度

我们用相对误差（RE）来衡量我们数据重构方法的准确性。

4.5.2 频数估计的界限

$E(y_1^i)=x^{i}p$

根据霍夫丁不等式，根据$(p+\beta 1)x^i<y_1^i<(p-\beta 1)x^i$ 求出我们的频数估计的相对误差大于$\beta 1/p$。

4.5.3 联合频数估计的界限

$E(y_1^{ij})=x^{ij}{p}^2$

4.6 复杂性分析

为了证明我们提出的方法理论上的高效，我们进行了时间复杂度分析和通信成本分析。在以下分析过程中，我们假定有n个用户和m个物品。

4.6.1时间复杂度

本文提出的方法包括两部分：数据扰动和数据重构。
数据扰动通过决定每个物品是否输出得到扰动的历史数据，因此时间复杂度为$O(m)$。
数据重构是输出每个物品的频数和每两个物品同时出现的频数。频数估计需要$O(m)$，联合频数估计需要$O(m^2)$，因此时间复杂度为$O(m^2)$。
数据扰动过程和数据重构过程分别是在基于普通和无隐私保护的协作过滤中对数据收集和数据计数的补充。数据扰动的时间复杂度等于数据收集的时间复杂度，因为用户的历史数据最多可以包含 m 个项目。数据重建的时间复杂度比数据计数的时间复杂度低，因为计算 n 个用户的 m-vector 和 mxin 矩阵的统计量分别需要计算频率和联合频率。因此，我们的数据扰动方法和数据重建方法的额外时间成本被限制在可接受的范围内。

4.6.2通信成本分析 【通信成本高】

我们提出的方法的通信成本取决于用户发送的项目数量。假设用户$U_u$的项目数是$x_u$，根据数据扰动法，其扰动数据中包含的项目数的期望值是$x_{u}p+(m-x_u)(1-p)$。请注意，通过使用简洁直方图[1]和 LDPMiner[29]等编码技术，可以降低这一成本。然而，在这项工作中，我们主要关注于通过数据重建来提高推荐的准确性，而将降低通信成本的任务留给了以后的工作。

5.Experiment

在这一部分，我们通过实验来评估我们提出的方法。

5.1 实验方法

5.1.1 数据集

本文采用两个公开数据集，Movielens 100k dataset;Jester-data-3 dataset。
因为我们侧重保护历史信息而不是用户的评分信息，我们将评分都转化为二进制评分（已评分为1未评分为0）。

5.1.2 对比方案

为了评估我们的性能，我们与如下几个算法进行比较。

• D2P[14]，在个性化推荐的背景下提供差别化的隐私保护。我们将距离参数λ设置为0，因此D2P的隐私本质上与我们的方法相同。
• Basic RAPPOR(B_RA)[10]，是一种经典的位置差分隐私机制。本文中，我们把多个历史项目看作一元编码，然后用B_RA扰动编码并进行频率估计。B_RA不进行联合频率估计，因此，我们直接从扰动的数据集中计算联合频率。

如第2.1节所示，在本地环境中有几种不同的隐私推荐解决方案。然而，这些解决方案大多数并不适用我们提出的应用场景。例如，[24.25]目标是保护用户的历史评分，[34]和[35]在非协同过滤推荐中确保用户的隐私。[18,36,43]应用于矩阵服务化推荐，而[23]则专注于基于用户的协同过滤推荐。

D2P是一个差分隐私的协同过滤框架，和我们提出的方法一样，它在用户端扰动用户的历史数据，然后在服务器侧基于扰动的历史数据做出推荐。我们选择它作为我们提出的方法的竞争者之一。

5.1.3 评估指标

我们通过两个方面对本方法进行评估：估计的准确性和推荐的准确性
从两方面衡量本方法的性能：估计的准确性（频数估计和联合频数估计）和推荐结果的准确性
估计的准确性（平均相对误差）(4.5)


推荐结果的准确性（Accuracy）(3.4)

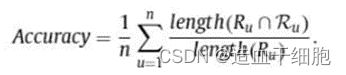
5.1.4 参数设置

推荐方法的参数设置如下。首先，Deshpande[5]表明，当n的值为0.3和0.6时，基于条件概率的方案获得了一致的良好性能，并且他们在实验中使用了n = 0.5的值，因此，我们在提出的方法和比较的方法中使用了相同的设置。其次，我们将隐私预算设置为 0.1-0.9。因为许多研究都认为隐私预算通常应该小于1[12，16，26]。第三，如定理 1所示，我们将数据扰动方法的选择概率 p 设置为$e^{\epsilon }/(e^{\epsilon }+1)$。最后，我们把推荐数量设置为 10- 100。

5.1.5 实验设置

隐私保护推荐方法的推荐结果可以是任意 N 个项目，因此每个推荐的评估结果可能不同。因此，对于每个目标用户，我们对 1000 个独立试验运行本方法和比较的方法，然后使用每个项目的平均推荐概率来评估估计准确性和推荐准确性。

5.2 实验结果

5.2.1 实验结果一览

如Figs2和Figs3所示，实验结果显示我们的方法在两方面的表现都优于对比方法。
首先，我们的方法有更高的推荐精度。我们建议读者先看看图 2。当隐私预算ε设置为 0.9，推荐数设置为 100 时，D2P、B_RA 和我们提出的方法的推荐准确率分别为 5.96%、6.03% 和 40.93%。这表明我们提出的方法在推荐准确率方面明显优于 D2P 和 B_RA。
其次，与比较方法相比，我们提出的方法在隐私和准确性之间有更好的平衡。当推荐数量设置为 100 时，隐私预算ε分别设置为 0.1、0.5 和 0.9，因此在 ML 数据集中使用我们提出的方法对应的推荐精度6.00%，17.47%，40.93%。而 B_RA 的推荐准确率仅从 4.30%提高到4.94%再到6.03%，与 D2P 基本持平约5.70%。这意味着我们提出的方法可以随着隐私预算的增加而大大提高准确性。
其他设置中的实验结果也支持我们提出的方法所获得的优势。

5.2.2 实验结果的分析

与比较的方法相比，我们提出的方法可以获得更高的推荐精度，并在隐私和准确性之间取得更好的平衡。本方法的进步主要来自数据重构过程。表 2 和表 3 分别显示了在 Movielens 数据集和 Jester 数据集上使用我们提出的方法和比较方法得出的相对误差。我们对实验结果做了两个结论。
一方面，我们的数据重建方法可以显著降低数据扰动过程带来的误差。我们建议读者首先查看表 2 和表 4 中最后一列显示的结果，其中ε= 0.9。

• 对于频率估计，D2P，B_RA 和我们提出的方法在 Movielens (Jester)数据集上获得的相对误差为8.45( 110.62)，0.29(0.09)和 0.12(0.07)。这些实验结果表明，我们提出的方法和 B_RA 获得的平均相对误差显著低于D2P获得的平均相对误差。这是因为我们的方法和 B_RA 从扰动数据中重构频率，而 D2P 没有。
  
• 对于联合频率估计，B_RA 和 DSP 的相对误差很大，而我们提出的方法相对误差较小。例如，上述设置的相对误差分别为 1.44(89.40)、46.12(314.48)和0.28(0.37)。DSP和 B_RA均不进行联合频率估计，但D2P的相对误差远小于B_RA。由于这两种方法产生的输出数量不同，这一结果是合理的。对于给定的历史数据，D2P输出的数量等于历史数据的大小，但是B_RA的数据量远远大于历史数据量。因此，扰动后的 B_RA 数据集中的联合频率远远大于D2P数据集中的联合频率，导致较大的相对误差。我们提出的方法的相对误差比比较的方法小得多，这是因为我们的方法从扰动数据中重构联合频率，而 B_RA和DSP没有。

另一方面，随着隐私预算的放宽，我们的数据重建方法得到的相对误差显著降低。如表2和表3所示，当隐私预算设置为 0.1、0.5 和 0.9 时，我们的频率估计在Movielens(Jester)的相对误差为1.35(0.69)、0.26(0.17)和 0.12(0.07)，我们的联合频率估计的相对误差分别是24.00(29.52)、0.95( 1.18)和 0.28（0.37）。对于B_RA，频率估计的相对误差在ML1000(Jester)数据集上也显示出明显的下降趋势，即从2.51(2.01)至 0.51(0.34)，然后是0.29(0.09)。然而，由于联合频率估计的相对误差太大，即使在过于宽松的隐私预算下，也无法提供准确的推荐结果。对于 D2P，频率估计和联合频率估计的相对误差几乎相同，即在 Movielens (Jester)数据集上的频率估计和联合频率估计分别约为 8.45(1.44)和 111(90)。这意味着，随着隐私预算的放松，D2P 的性能也没什么提高。

5.3 历史数据规模的影响

为了分析历史数据的规模对推荐准确性的影响，我们从Movielens分出10个不同的数据集，每个数据集选100,200，…，1000个最高频出现的物品。构建数据集的统计学信息如下图。

如Fig4 所示，对于我们提出的方法和比较的方法，推荐精度都随着历史数据量的增加而降低。正如我们在5.2.2节中所讨论的，推荐精度取决于数据扰动的精度，如Table 5 所示，相对误差随着历史数据的大小而增加。因此，我们认为历史数据越大，就越难进行好的数据重构，推荐的准确性也就越差。
虽然推荐精度会随着历史数据量的增加而降低是不可避免的，但是与比较方法相比，我们提出的方法受历史数据量的影响更小。例如，当ε=0.9 时，当历史数据的大小从 100 增加到 1000 时，我们提出的方法的推荐精度从98.19%下降到88.84%，但是 D2P 和 B_RA 的推荐精度呈现出急剧下降的趋势，即前者从47.49%下降到4.63%，后者从 53.75 %下降到 6.36%。

5.4 计算时间分析

在这一部分，我们评估了我们提出的数据扰动方法和数据重建方法的计算时间。在配备英特尔酷睿 i7-3770 CPU、8核处理器和 16GB RAM 的 Linux 工作环境运行我们的方法和比较算法。图 5 和图 6 分别说明了我们提出的方法以及比较方法在 Movieiens 数据集和 Jester 数据集上的计算时间。由于两个数据集的结论相似，我们仅讨论了Movielens 数据集的结果。
对于数据扰动方法，如Fig5所示，D2P、B_RA和本文算法每个用户扰动数据的时间分别是$5.0\times 10^{-4}s,1.9\times 10^{-3}s,1.9\times 10^{-3}s$。这表示B_RA和我们的方法需要更多的时间去扰动用户历史数据。当然，这依旧是一段很短的时间。
对于数据重建方法，正如我们在第 4.6.1 节中所讨论的，该计算主要包括数据计数和数据重建。理论结果表明，数据重构的时间复杂度小于数据计数的时间复杂度。如图 5b和 5c 所示，用于频率估计和联合频率估计的data count(数据重构)的计算时间是0.13$(9.0\times 10^{-4}s)$和 217.75s(8.13s)。无隐私保护的基于物品的协同过滤也需要对数据进行计数，因此我们提出的数据重建方法对现有基于项目的协同过滤推荐的计算时间影响很小。

6.Conclusion

本文提出了一种新的基于局部差异私有项目的协同过滤框架。在该框架内，我们引入了以下算法。第一种是保护用户隐私的数据扰动机制，并被证明满足差分隐私。第二种是相似度重构方法，通过计算任意一对项目之间的相似度得分来提高推荐的准确性。在真实数据集上的实验表明，与最先进的方法相比，我们提出的框架大大提高了推荐的准确性以及隐私和准确性之间的平衡。该方法也可用于 IoT 环境下的隐私保护数据聚合。一方面，智能网关利用所提出的数据扰动方法，对物联网设备采集的感知数据进行扰动，以确保用户隐私。另一方面，服务器通过使用所提出的数据重建方法，重建感觉数据的统计特性，以从扰动的感觉数据获得更准确的集合数据。