二叉树总结

按照labuladong做了二叉树的题，在此稍微总结一下

1.二叉树的定义：

python

class TreeNode:
     def __init__(self, val=0, left=None, right=None):
         self.val = val
         self.left = left
         self.right = right

c++

  struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode() : val(0), left(nullptr), right(nullptr) {}
      TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
      TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };

2.递归遍历二叉树

递归调用tarverse函数，前序（根左右），中序（左根右），后序（左右根）

void traverse(TreeNode root) {
    // 前序遍历
    traverse(root.left)
    // 中序遍历
    traverse(root.right)
    // 后序遍历
}

3.二叉树递归的思路

主要是看在根节点需要做些什么，注意递归是要用终止条件，需要判断根节点不为空再继续操作

    if (root == null) {
        return null;
    }

4.题目汇总（粉色的是不太熟的）

1）翻转二叉树：调换左右节点即可

2）填充二叉树节点的右侧指针：利用辅助函数，对父节点及其左右子节点进行连接

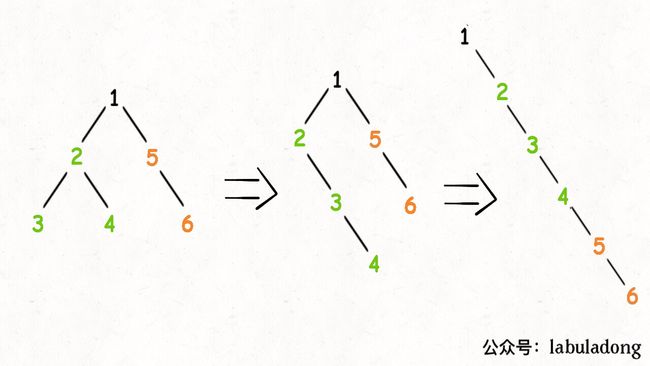
3）将二叉树展开为链表：这道题比较复杂，需要搞清楚展开的过程

234的子树的过程：首先将左右子树拉平作为链表，然后将左子树变成右子树，原来的右子树接到左子树上

4）构造最大二叉树：找到数组中的最大值和其相应的索引，最大值前面的是左子树，后面的是右子树

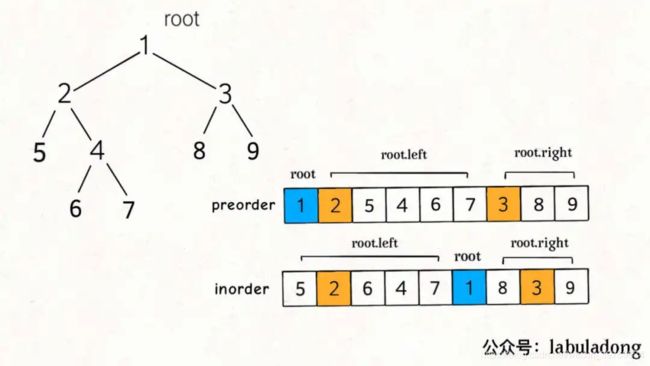
5）通过前序和中序遍历结果构造二叉树：分析前序，中序，左右子树和根节点的关系。根据索引的关系，构造左右子树

6）通过后序和中序遍历结果构造二叉树：类似5）

7）寻找重复的子树：将某节点的子树表现成序列化，遍历二叉树，看是否有与该节点子树一样的。在这里可以用字典的形式来储存所有节点的子树。

8）寻找第k小的元素：BST 中序遍历就是升序排序结果，遍历的第k个元素就是第k小的

9）BST 转化累加树：相当于是从大的到自己的和，则需要把中序排序反过来，左右节点位置调换，递归时求和，再代替根节点的值即可

10）判断 BST 的合法性：合法的BST是整个左子树都要小于根节点的值，整个右子树都大于根节点的值，则左子树root.val，通过辅助函数helper（root，min，max）递归得到

11）在 BST 中搜索一个数：也可以利用左右子树的大小关系，例如给定数小于根节点则在左子树搜索

void BST(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target) 
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}

12）在 BST 中插入一个数：使用的和上一题类似的框架，先找到合法的位置，到头根节点是空的，则把需要插入的数放到空节点上。

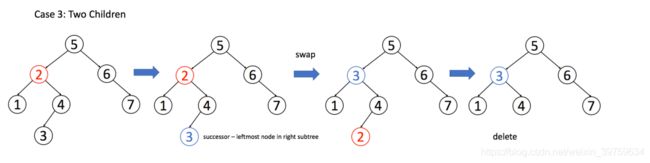
13）在 BST 中删除一个数：跟插入操作类似，先「找」再「改」，有三种删除的情况

情况3：左右子树都不为空，找到右子树中最小的代替自己/左子树中最大的代替自己

4.写代码经常出现问题的一些点：

1）返回一颗二叉树：只需要返回其根节点即可 return root

     构造二叉树：Treenode（root.val)，成功构造了根节点，在对左右子树分别赋值即可

2）递归函数traverse，到底是traverse（root.left), traverse(root.right)，什么时候两个都写，什么时候只需要写一个：

3）递归的过程想不清楚：

在这里参考这篇博客：递归就是有去（递去）有回（归来），如下图所示。“有去”是指：递归问题必须可以分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决，就像上面例子中的钥匙可以打开后面所有门上的锁一样；“有回”是指 : 这些问题的演化过程是一个从大到小，由近及远的过程，并且会有一个明确的终点(临界点)，一旦到达了这个临界点，就不用再往更小、更远的地方走下去。最后，从这个临界点开始，原路返回到原点，原问题解决。

个人理解是到了最后的终止条件开始返回，但是求解还是正向的，所以可以思考终止前的最末端的情况看一下是如何求解的。整体思路如下：

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 在将问题转换为子问题的每一步，解决该步中剩余部分的问题
        solve;                // 递去
        recursion(小规模);     // 递到最深处后，不断地归来
    }
}

function recursion(大规模){
    if (end_condition){      // 明确的递归终止条件
        end;   // 简单情景
    }else{            // 先将问题全部描述展开，再由尽头“返回”依次解决每步中剩余部分的问题
        recursion(小规模);     // 递去
        solve;                // 归来
    }
}

4）按照以上有递去归来和归来递去两种模型，在代码中也是有时先写递归函数，再写操作，有时把递归函数放在后面。两种写法都可以，本质上没有太多差别。

5）对于判断型的题，return的是写true还是false？需要仔细想明白，判断型的return有两处一处是终止条件，一处是操作，如果是搜寻的话到了根节点为空还未搜索到则应该返回false，如果是判断合法性，到了根节点说明之前是合法的需要返回true