链式二叉树及相关操作(前,中,后,层序遍历)
欢迎来到 Claffic 的博客
“春来无事,只为花忙。”
前言:
上一期给大家介绍了二叉树的一种顺序结构:堆,这一期承接上一期,给大家继续介绍二叉树的另一种结构:链式结构。
目录
Part1:链式二叉树?
1.前情提要
2.创建一颗二叉树
Part2:相关操作实现
2.1遍历操作
2.1.1前序遍历
2.1.2中序遍历
2.1.3后序遍历
2.1.4层序遍历
2.2其他操作
2.2.1二叉树结点个数
2.2.2二叉树高度
2.2.3第k层结点个数
2.2.4判断是否为完全二叉树
2.2.5查找为x的结点
2.2.6二叉树销毁
Part1:链式二叉树?
1.前情提要
这里的链式二叉树其实就是利用每个结点的左孩子和右孩子关系来创建的,方便快速手搓一个简单的二叉树。
2.创建一颗二叉树
其实方法很简单:
确定结点的结构 --> 根据左右孩子关系链接
//结点的结构
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
//新结点的创建
BTNode* BuyNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
//链接
BTNode* CreatTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
到这里,这颗二叉树的样子就有了:
Part2:相关操作实现
2.1遍历操作
遍历可以清晰的明确二叉树的结构。
二叉树的遍历是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个结点只操作一次。
按照规则,二叉树的遍历(按访问顺序)有:
前序遍历:根节点-->左节点-->右结点;
中序遍历:左节点-->根节点-->右结点;后序遍历:左节点-->右结点-->根节点;
层序遍历:简单说,就是二叉树由上到下,由左到右遍历。
2.1.1前序遍历
由于每次遍历都是 根节点-->左节点-->右结点,所以非常适合用递归来实现遍历。
前序遍历图解
面对二叉树遍历,既要看到大树,又能看到小树;
可以看出,首先由顶部根节点进入,再递归左边,遇到空结点返回,再递归右结点... ...依次反复
那么就可以上代码了:
//前序遍历
void PreOder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PreOder(root->left);
PreOder(root->right);
}
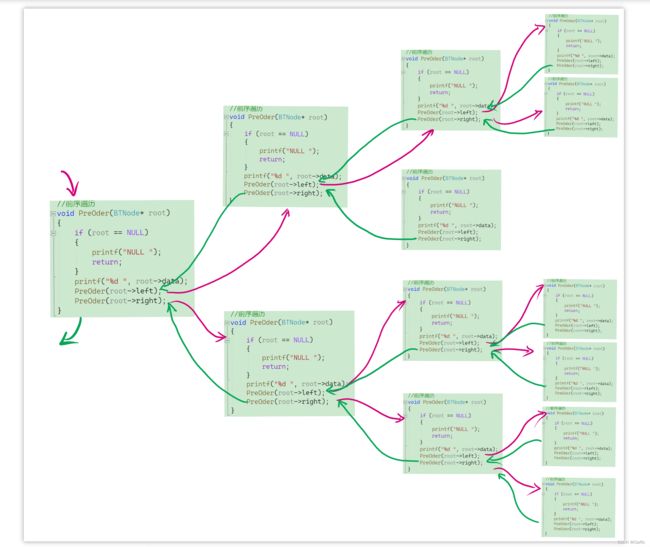
为了更详细的理解,这里画一下代码的递归图解:
学会了前序遍历,剩余的中序遍历和后序遍历也就会了,它们之间只有访问结点的顺序不同。
2.1.2中序遍历
//中序遍历
void InOder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOder(root->left);
printf("%d ", root->data);
InOder(root->right);
}
2.1.3后序遍历
//后序遍历
void PostOder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOder(root->left);
PostOder(root->right);
printf("%d ", root->data);
}
2.1.4层序遍历
层序遍历与前三种遍历不同;
这里直接上演示图吧:
简单解释:
双亲结点弹出,两个孩子节点就入 队列 ;
是的,这里用到了队列 先入先出 的特点。
上代码:
// 层序遍历
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q,root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
QueueDestroy(&q);
}
2.2其他操作
2.2.1二叉树结点个数
这里利用了分治思想,
即让每个根节点去统计孩子结点个数,再依次向上汇报;
还是利用递归:
// 二叉树节点个数 分治思想
int BinaryTreeSize(BTNode* root)
{
return root == NULL ? 0 :
BinaryTreeSize(root->left)
+ BinaryTreeSize(root->right)
+ 1; // +1是自己
}
2.2.2二叉树高度
二叉树的高度,是取左子树和右子树高度中最大者,
所以可以先利用递归分别保存左右子树的高度,再返回较大值:
//二叉树高度
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int Heightleft = BinaryTreeHeight(root->left) + 1;
int Heightright = BinaryTreeHeight(root->right) + 1;
return Heightleft >= Heightright ? Heightleft : Heightright;
}
2.2.3第k层结点个数
同样的,第k层结点个数包含左子树结点个数与右子树结点个数:
//第k层节点个数
int BinaryTreeKLevel(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1) // 顶部根节点的特殊情况
return 1;
return BinaryTreeKLevel(root->left, k - 1)
+ BinaryTreeKLevel(root->right, k - 1);
}
2.2.4判断是否为完全二叉树
还记得完全二叉树吗?
它的特点是 空结点连续 ,我们就可以利用这一个特点来判断;
判断一层连不连续,正好用到前面的层序遍历思想,利用 队列 来实现:
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
//判断
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
2.2.5查找为x的结点
分左右结点来查找,若有多个满足条件的结点,返回先找到的结点指针:
//查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* lret = BinaryTreeFind(root->left, x);
if (lret)
return lret;
BTNode* rret = BinaryTreeFind(root->right, x);
if (rret)
return rret;
return NULL;
}
2.2.6二叉树销毁
这个销毁也是要逐个销毁的,也要用到递归,分左子树销毁和右子树销毁:
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);
}
代码已上传至 我的gitee
拿走不谢~
总结:
链式二叉树的实现~ 主要掌握四种遍历:前中后序遍历和层序遍历,尽量搞懂是如何递归的,才会有更深刻的记忆~
码文不易
如果你觉得这篇文章还不错并且对你有帮助,不妨支持一波哦