LeetCode高频题28. 实现 strStr()：KMP算法，LeetCode疯了，竟然标记为easy

LeetCode高频题28. 实现 strStr()：KMP算法，LeetCode疯了，竟然标记为easy！

提示：本题是系列LeetCode的150道高频题，你未来遇到的互联网大厂的笔试和面试考题，基本都是从这上面改编而来的题目
互联网大厂们在公司养了一大批ACM竞赛的大佬们，吃完饭就是设计考题，然后去考应聘人员，你要做的就是学基础树结构与算法，然后打通任督二脉，以应对波云诡谲的大厂笔试面试题！
你要是不扎实学习数据结构与算法，好好动手手撕代码，锻炼解题能力，你可能会在笔试面试过程中，连题目都看不懂！比如华为，字节啥的，足够让你读不懂题

基础知识：
【1】KMP算法预备知识：字符串match的每一个位置i之前的字符串，前缀与后缀匹配的最大长度是多少
【2】KMP算法：在字符串s中搜索匹配查找match字符串，如果能找到返回首个匹配位置i，否则返回-1

---

题目

实现 strStr() 函数。

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回 -1 。

说明：

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/implement-strstr
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

---

一、审题

示例 1：

输入：haystack = “hello”, needle = “ll”
输出：2
示例 2：

输入：haystack = “aaaaa”, needle = “bba”
输出：-1

提示：

1 <= haystack.length, needle.length <= 104
haystack 和 needle 仅由小写英文字符组成

---

KMP算法：LeetCode竟然将其标记为简单easy，疯了！

本题就是啥呢？
在s字符串中找match字符串，看看match是否出现在s中，若出现，返回匹配上的首个位置index

这就是大名鼎鼎的KMP算法啊！！
LeetCode竟然将其标记为easy？？？？？
怎么想的！！！

这题目显然是super hard的难度哇

当然你暴力解解释很简单

---

暴力解当然简单，但是这不是面试官要的解，显然只能给你0分

来到s的i位置，从i开始，对比match的首字符j=0位置，从头开始遍历对比一遍
中途一点ij对应不上，i++，j=0，从头又开始对比一遍
直到所有位置对比完，j=M，末尾了还，看看啥时候能对比上，返回i

这暴力到啥时候才能对比完？？？
当然了你用系统函数……那就不是优化了啊

这么搞
字符串不是有一个函数吗：s.startsWith(match)，请问s是否以match开头？有就返回位置i
否则返回-1

比如：

        String s = "abcdef";
        String match = "abc";
        System.out.println(s.startsWith(match));

返回Boolean值是否

true

那么我们可以这么搞：
来到s的i位置，咱们截取s的i–N-1范围上的字符串=str来
看看str是否以match开头呢？
是：则i位置就是第一个匹配上的首字符
否则：就-1

这很容易吧
外围调度i是o(n)
内部startsWith函数复杂度又是一个o(n)，显然
整体复杂度o(n^2)

这种复杂度笔试可以AC，但是面试绝对0分！

手撕代码：

        //复习
        public int strStrReview(String s, String match) {
            if (s.compareTo("") == 0 && match.compareTo("") == 0) return 0;
            if (s.compareTo("") == 0) return -1;
            if (match.compareTo("") == 0) return 0;//情况过滤好
            if (s.length() < match.length()) return -1;

            //下面都有
            for (int i = 0; i < s.length(); i++) {
                String str = s.substring(i);//后续所有
                if (str.startsWith(match)) return i;
            }
            //全部找完，没有，就是-1
            return -1;
        }

测试一把：

    public static void test(){
        Solution solution = new Solution();
        String s = "abcdef";
        String match = "cde";
        System.out.println(s.startsWith(match));

        System.out.println(solution.strStr(s, match));
        System.out.println(solution.strStrReview(s, match));
    }

    public static void main(String[] args) {
        test();
    }

问题不大：

false
2
2

LeetCode测试：

class Solution {
    public int strStr(String haystack, String needle) {
        //复习
            if (haystack.compareTo("") == 0 && needle.compareTo("") == 0) return 0;
            if (haystack.compareTo("") == 0) return -1;
            if (needle.compareTo("") == 0) return 0;//情况过滤好
            if (haystack.length() < needle.length()) return -1;

            //下面都有
            for (int i = 0; i < haystack.length(); i++) {
                String str = haystack.substring(i);//后续所有
                if (str.startsWith(needle)) return i;
            }
            //全部找完，没有，就是-1
            return -1;
        }
}

看来也不慢，但是这事笔试
面试的话，下面KMP算法

---

面试最优解：KMP算法，o(n)速度，极快

KMP算法预备知识：字符串match的每一个位置i之前的字符串，前缀与后缀匹配的最大长度是多少

关于KMP算法，我前面已经花了老多心思给你讲过了
你得好好看透这俩文章
什么是KMP算法？
它要准备next预设信息数组干嘛的？
next是如何起到避免重复暴力匹配的？即舍弃思想；

KMP两大重要重要重要文章：
KMP两大重要重要重要文章：
KMP两大重要重要重要文章：

【1】KMP算法预备知识：字符串match的每一个位置i之前的字符串，前缀与后缀匹配的最大长度是多少
【2】KMP算法：在字符串s中搜索匹配查找match字符串，如果能找到返回首个匹配位置i，否则返回-1

你得去那看透了！！！
我再提一嘴
next收集的是match串（即needle串的信息）
next主要就是收集match的i前面字符串中，0–i-1上，前缀=后缀的最长匹配长度

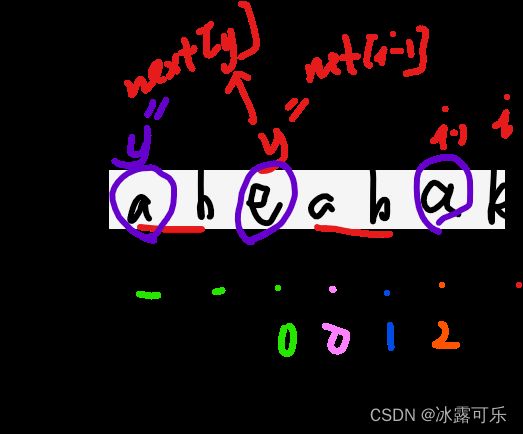
比如：
人为规定next[0]=-1,next[1]=0
也就是0之前，压根没有字符串，前缀与后缀的匹配最大长度为-1
1位置之前就一个字符串0位置，有前缀没后缀，所以匹配长度最大为0
这俩人为规定好的

从i开始就要看看0–i-1上的前缀和后缀，匹配=相等的最大长度是多少？
上图中i=2，前面a!=b所以最大匹配长度0
上图中i=3，前面a!=e所以最大匹配长度0
上图中i=4，看next[i-1]=0，它不仅代表，i之前的字符串前缀=后缀匹配的最长长度，
它其实还是指向i-1那个字符与前面第一个无法匹配的位置：即y=next[i-1]=0位置与当前i-1位置压根不匹配
——搞清楚这个含义非常非常重要

所以呢，我们要看看此刻i-1字符能与y=next[i-1]匹配吗？
哟？i-1字符是a，y=next[i-1]=0字符也是a，巧了能匹配，所以呢能匹配上的最大长度就是next[i-1]+1=1
让y++，下一次直接让i字符与新y继续对比……
这就是next[i]的求法，看的就是i-1的信息与i-1字符相等的状况

如果i-1字符和y=next[i-1]位置还是不相等，那还需要看y的情况，y>0的话，y=next[y]，即y不断往前捣鼓，看看能不能找到和i-1字符相等的字符，这样就可以填好next了。
如果一直往前捣鼓，发现y<=0了，说明y到了0位置了都没对上，没法对比了，next[i]=0,然后i++，继续求别next信息

去看那个文章啊！！！
手撕代码：必须会了

        //KMP算法就是干这事的
        //KMP算法预备知识：字符串match的每一个位置i之前的字符串，前缀与后缀匹配的最大长度是多少？
        //next数组啥意思呢？**next[i]代表：match串的i位置前面，前缀与后缀相匹配的最大长度。**
        //【1】即0--i-1范围上前后缀匹配的最大长度。
        //【2】next[i]还代表，**0--i-1范围上第一个与i位置不匹配的位置。**
        public static int[] writeNextInfo(char[] m){
            int M = m.length;
            int[] next = new int[M];
            //（1）咱们人为规定，**next[0]=-1,next[1]=0**
            next[0] = -1;//next[1]=0默认
            int i = 2;//2开始
            int y = next[i - 1];//它是0--i-1已经匹配的长度，也是咱们直接对标跟i-1没有匹配上的那个位置
            while (i < M){
                //（2）来到i位置，0--i-1的next信息已经具备，咱只需要根据前面的状况推导i位置的next信息即可
                //（3）咱只需要确认y=next[i-1]位置的字符，与i-1位置的字符c是否相等？【next[i-1]>0的话】
                if (m[y] == m[i - 1]) {
                    //**如果相等**，那next[i]=next[i-1]+1;
                    next[i++] = y + 1;//它是0--i-2已经匹配的长度+1
                    y++;//这个别忘了--这样的话，咱们可以接着往下比i+1位置--可能还会有更长的长度
                }
                //**如果不相等**，那就继续看y=next[y]位置的字符，与i-1位置的字符c是否相等？
                else if (y > 0) y = next[y];//往前整
                    //如果next[y]<=0，说明，往前没有字符了，直接令next[i]=0；一个都没有匹配的
                else next[i++] = 0;//到头了都没有匹配上。
                //（4）i++，直到i越界
            }

            return next;
        }

测试一下整个函数：

    public static void test2(){
        String match = "abcabck";
        char[] m = match.toCharArray();
        Solution solution = new Solution();
        int[] next = solution.writeNextInfo(m);
        for(Integer i : next) System.out.print(i +" ");
    }
    public static void main(String[] args) {
//        test();
        test2();
    }

你仔细看看next数组是不是整个含义：i-1之前的前缀=后缀的最大匹配长度

-1 0 0 0 1 2 3 

下面讲KMP算法如何舍弃不必要的重复对比的

KMP算法：在字符串s中搜索匹配查找match字符串，如果能找到返回首个匹配位置i，否则返回-1

咱们先说这个KMP算法的对比流程：
（0）对match串构建next信息
（1）咱们拿m的y=0位置开始与s的x=i位置一个一个往后面匹配
（2）如果发现x字符与y字符相等！则x++，y++；回到（2）继续比对——匹配上了呗
（3）如果发现x字符与y字符不相等！那直接宣告s中i–j-1这一段，谁开头都没法匹配处m串来！
【舍弃i–j-1这一段开头的情况，不要对比了（图中粉色那段）】，下一次直接默认s从j开头从新匹配
（4）同时，还不是让y直接退回到m串的0位置从头匹配，而是让y=next[y]（暂时叫它y2），直接判断x字符是否等于y2字符
若是相等，去（2）继续对比
若是不相等，去（3）继续对比
（5）如果不等的情况下发现next[y]=-1的话，说明m从y=0位置也跟x字符不相等，x++即可；去s的后面继续对比；
（6）如果x越界，或者y越界，发现y=M，则说明整个m串都匹配好了，返回结果x-y。因为x-m的长度M就是s中首个匹配上的位置i。

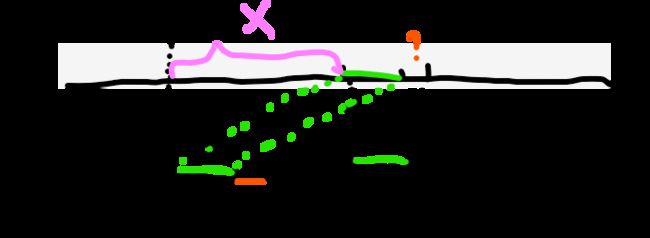
关于KMP算法舍弃的核心思想，一定要去看【2】那个文章
这里一句两句讲不清楚的，我之前花了重心思讲过的。

代码如下：

        //KMP算法的对比流程：
        public int KMPSearchMatchInStr(String s, String match){
            if (s == null || s.equals("") || s.length() < match.length()) return -1;

            int N = s.length();
            int M = match.length();

            char[] str = s.toCharArray();
            char[] m = match.toCharArray();

            //对match串构建next信息
            int[] next = writeNextInfo(m);

            //（1）咱们拿m的y=0位置开始与s的x=i位置一个一个往后面匹配
            int x = 0;
            int y = 0;
            while (x < N && y < M){
                //（2）如果发现**x字符与y字符相等**！则x++，y++；回到（2）继续比对
                if (str[x] == m[y]){
                    x++;
                    y++;//往后滑动即可
                }
                //（3）如果发现**x字符与y字符不相等**！那直接宣告s中i--j-1这一段，谁开头都没法匹配处m来！
                // 【省掉i--j-1这一段开头的情况，不要对比了】，下一次直接默认s从j开头从新匹配
                //（4）同时，还不是让y直接退回到m的0位置从头匹配，而是让**y=next[y]**（暂时叫它y2），
                // 直接判断x字符是否等于y2字符
                //若是相等，去（2）继续对比
                //若是不相等，去（3）继续对比
                //（5）如果不等的情况下发现next[y]=-1的话，说明m从y=0位置也跟x字符不相等，x++即可；去s的后面继续对比
                else if (y == 0) x++;
                else y = next[y];//如果y>0的话，继续回去对比
            }//这个代码是非常非常简单的，一定要搞清楚这个逻辑
            //（6）如果x越界，或者y越界，发现y=M，则说明整个m都匹配好了，返回结果x-y。
            // 因为x-m的长度M就是s中首个匹配上的位置i。
            return y == M ? x - y : -1;
        }

KMP算法的代码是非常非常简单的，有了next数组
实际上对比s的x和match的y
相等咱x++，y++
不相等，看看y=0吗？是等于0的话，说明压根就一直没有对上，让x++
不相等，看看y>0吗？是大于0的话，y=next[y]，可以考虑直接去对比之前的那个y和现在的x
这逻辑很简单

整体复杂度o(n）
测试一把：

    public static void test(){
        Solution solution = new Solution();
        String s = "abcdef";
        String match = "cde";
        System.out.println(s.startsWith(match));

        System.out.println(solution.strStr(s, match));
        System.out.println(solution.strStrReview(s, match));
        System.out.println(solution.KMPSearchMatchInStr(s, match));
    }


    public static void main(String[] args) {
        test();
//        test2();
    }

问题不大：

2
2
2

看看lleetcode的反应

class Solution {
    //KMP算法就是干这事的
        //KMP算法预备知识：字符串match的每一个位置i之前的字符串，前缀与后缀匹配的最大长度是多少？
        //next数组啥意思呢？**next[i]代表：match串的i位置前面，前缀与后缀相匹配的最大长度。**
        //【1】即0--i-1范围上前后缀匹配的最大长度。
        //【2】next[i]还代表，**0--i-1范围上第一个与i位置不匹配的位置。**
        public int[] writeNextInfo(char[] m){
            if (m.length == 1) return new int[] {-1};//太短没法搞的
            int M = m.length;
            int[] next = new int[M];
            //（1）咱们人为规定，**next[0]=-1,next[1]=0**
            next[0] = -1;//next[1]=0默认
            int i = 2;//2开始
            int y = next[i - 1];//它是0--i-1已经匹配的长度，也是咱们直接对标跟i-1没有匹配上的那个位置
            while (i < M){
                //（2）来到i位置，0--i-1的next信息已经具备，咱只需要根据前面的状况推导i位置的next信息即可
                //（3）咱只需要确认y=next[i-1]位置的字符，与i-1位置的字符c是否相等？【next[i-1]>0的话】
                if (m[y] == m[i - 1]) {
                    //**如果相等**，那next[i]=next[i-1]+1;
                    next[i++] = y + 1;//它是0--i-2已经匹配的长度+1
                    y++;//这个别忘了--这样的话，咱们可以接着往下比i+1位置--可能还会有更长的长度
                }
                //**如果不相等**，那就继续看y=next[y]位置的字符，与i-1位置的字符c是否相等？
                else if (y > 0) y = next[y];//往前整
                    //如果next[y]<=0，说明，往前没有字符了，直接令next[i]=0；一个都没有匹配的
                else next[i++] = 0;//到头了都没有匹配上。
                //（4）i++，直到i越界
            }

            return next;
        }

    //LeetCode
        public int strStr(String haystack, String needle) {
            if (haystack.compareTo("") == 0 && needle.compareTo("") == 0) return 0;
            if (haystack.compareTo("") == 0) return -1;
            if (needle.compareTo("") == 0) return 0;//情况过滤好
            if (haystack.length() < needle.length()) return -1;

            int N = haystack.length();
            int M = needle.length();

            char[] str = haystack.toCharArray();
            char[] m = needle.toCharArray();

            //对match串构建next信息
            int[] next = writeNextInfo(m);

            //（1）咱们拿m的y=0位置开始与s的x=i位置一个一个往后面匹配
            int x = 0;
            int y = 0;
            while (x < N && y < M){
                //（2）如果发现**x字符与y字符相等**！则x++，y++；回到（2）继续比对
                if (str[x] == m[y]){
                    x++;
                    y++;//往后滑动即可
                }
                //（3）如果发现**x字符与y字符不相等**！那直接宣告s中i--j-1这一段，谁开头都没法匹配处m来！
                // 【省掉i--j-1这一段开头的情况，不要对比了】，下一次直接默认s从j开头从新匹配
                //（4）同时，还不是让y直接退回到m的0位置从头匹配，而是让**y=next[y]**（暂时叫它y2），
                // 直接判断x字符是否等于y2字符
                //若是相等，去（2）继续对比
                //若是不相等，去（3）继续对比
                //（5）如果不等的情况下发现next[y]=-1的话，说明m从y=0位置也跟x字符不相等，x++即可；去s的后面继续对比
                else if (y == 0) x++;
                else y = next[y];//如果y>0的话，继续回去对比
            }//这个代码是非常非常简单的，一定要搞清楚这个逻辑
            //（6）如果x越界，或者y越界，发现y=M，则说明整个m都匹配好了，返回结果x-y。
            // 因为x-m的长度M就是s中首个匹配上的位置i。
            return y == M ? x - y : -1;
        }
}

LeetCode测试：


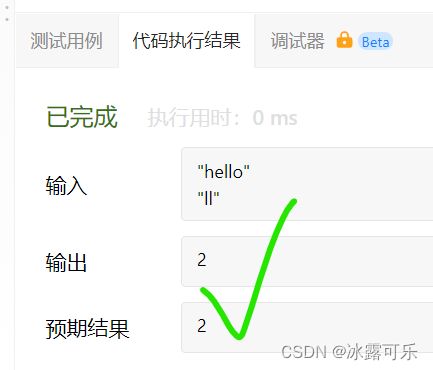
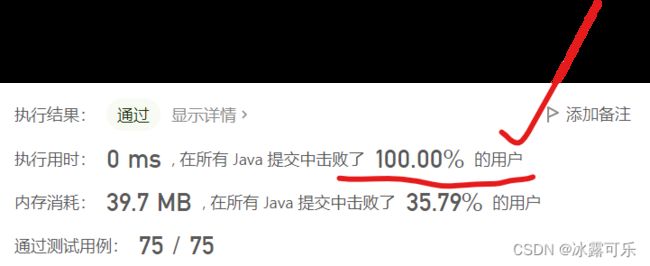
瞅瞅！！！
KMP算法做字符串匹配工作有多牛逼！！！
干掉100%的人的算法

复杂度o(n)
那叫一个快！！！！

可千万千万熟悉并掌握KMP的next数组如何生成的
看的就是i-1字符和next[i-1]的情况
有了next信息，就可以根据x和y处的字符相等情况来决定了
不等就看看next[y]的情况，当然还要可能y是不是>0
代码是非常非常容易的

---

总结

提示：重要经验：

1）本题可以用暴力startWith和substring函数解，复杂度o(n^2)，笔试AC
2）但是面试必定要用KMP算法，知道next数组是什么意思，知道用next舍弃没必要重复对比的字符串
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。